传染病的数学模型
此词条暂由Potatozh初译,未经审校,带来阅读不便,请见谅。
Mathematical models can project how infectious diseases progress to show the likely outcome of an epidemic and help inform public health interventions. Models use basic assumptions or collected statistics along with mathematics to find parameters for various infectious diseases and use those parameters to calculate the effects of different interventions, like mass vaccination programmes. The modelling can help decide which intervention/s to avoid and which to trial, or can predict future growth patterns, etc.
数学模型可以预测传染病如何发展,以显示流行病的可能结果,并有助于为公共卫生干预提供依据。 模型使用基本假设或统计数据来找到各种传染病的参数,并使用这些参数来计算不同干预措施(例如大规模疫苗接种计划)的效果。 建模可以帮助确定要避免使用的干预措施以及要进行尝试的干预措施,或者可以预测未来的增长模式等。
历史 History
The modeling of infectious diseases is a tool that has been used to study the mechanisms by which diseases spread, to predict the future course of an outbreak and to evaluate strategies to control an epidemic.[1]
传染病建模是一种工具,用于研究疾病传播的机制,预测爆发的未来过程以及评估控制流行病的策略。
The first scientist who systematically tried to quantify causes of death was John Graunt in his book Natural and Political Observations made upon the Bills of Mortality, in 1662. The bills he studied were listings of numbers and causes of deaths published weekly. Graunt's analysis of causes of death is considered the beginning of the "theory of competing risks" which according to Daley and Gani [1] is "a theory that is now well established among modern epidemiologists".
约翰·格伦特(John Graunt)在1662年根据《死亡率法案》撰写的《自然和政治观察》一书中,他是第一个系统地尝试量化死亡原因的科学家。他研究的法案是每周出版的死亡人数和原因清单。 格兰特对死亡原因的分析被认为是“竞争风险理论”的开端。根据戴利和加尼的说法,“竞争风险理论”是“现代流行病学家中已经建立的一种理论”。
The earliest account of mathematical modelling of spread of disease was carried out in 1760 by Daniel Bernoulli. Trained as a physician, Bernoulli created a mathematical model to defend the practice of inoculating against smallpox.[2] The calculations from this model showed that universal inoculation against smallpox would increase the life expectancy from 26 years 7 months to 29 years 9 months.[3] Daniel Bernoulli's work preceded the modern understanding of germ theory.
最早的疾病传播数学模型是1760年由丹尼尔·伯努利(Daniel Bernoulli)进行的。 受过医师培训的伯努利创建了一个数学模型来捍卫预防天花的接种方法。该模型的计算结果表明,普遍接种预防天花的疫苗可以将预期寿命从26岁7个月增加到29岁9个月。丹尼尔·伯努利(Daniel Bernoulli)的工作先于对细菌理论的现代理解。
In the early 20th century, William Hamer[4] and Ronald Ross[5] applied the law of mass action to explain epidemic behaviour.
在20世纪初期,威廉·哈默(William Hamer)和罗纳德·罗斯(Ronald Ross)运用群众行动定律来解释流行病行为。
The 1920s saw the emergence of compartmental models. The Kermack–McKendrick epidemic model (1927) and the Reed–Frost epidemic model (1928) both describe the relationship between susceptible, infected and immune individuals in a population. The Kermack–McKendrick epidemic model was successful in predicting the behavior of outbreaks very similar to that observed in many recorded epidemics.[6]
1920年代出现了仓室模型。 Kermack-McKendrick流行病模型(1927年)和Reed-Frost流行病模型(1928年)均描述了人群中易感,感染和免疫个体之间的关系。 Kermack–McKendrick流行病模型成功地预测了爆发行为,与许多已记录的流行病中观察到的行为非常相似。
Recently, agent-based models (ABMs) have been used in exchange for simpler compartmental models, e.g.,[7]. For example, epidemiological ABMs have been used to inform public health (nonpharmaceutical) interventions against the spread of SARS-CoV-2[8]. Epidemiological ABMs, in spite of their complexity and requiring high computational power, have been criticized for simplifying and unrealistic assumptions[9][10]. Still, they can be useful in informing decisions regarding mitigation and suppression measures in cases when ABMs are accurately calibrated[11].
最近,基于代理的模型(ABMs)已用于交换较简单的仓室模型,例如。 例如,ABMs已被用于提供公共卫生方面的(非药物)干预措施,以防止SARS-CoV-2的传播[8]。 虽然ABMs复杂且需要很高的计算能力,但是该模型仍然由于其简化和不切实际的假设而受到批评。 不过,在准确校准ABMs的情况下,它们对于提供有关缓解和抑制措施方面的决策还是有用的。
假设条件 Assumptions
Models are only as good as the assumptions on which they are based. If a model makes predictions that are out of line with observed results and the mathematics is correct, the initial assumptions must change to make the model useful.
模型仅与它们所基于的假设一样好。 如果模型做出的预测与观察到的结果不符并且数学是正确的,则必须更改初始假设以使模型结果有其用处。
- Rectangular and stationary age distribution, i.e., everybody in the population lives to age L and then dies, and for each age (up to L) there is the same number of people in the population. This is often well-justified for developed countries where there is a low infant mortality and much of the population lives to the life expectancy.
- 矩形和稳态时固定年龄分布,即人群中的每个人都活到L岁,然后死亡,并且对于每个年龄(至L),人群中的人数都是相同的。 对于婴儿死亡率较低且人群中大部分人都达到预期寿命的发达国家来说,这个假设通常是合理的。
- Homogeneous mixing of the population, i.e., individuals of the population under scrutiny assort and make contact at random and do not mix mostly in a smaller subgroup. This assumption is rarely justified because social structure is widespread. For example, most people in London only make contact with other Londoners. Further, within London then there are smaller subgroups, such as the Turkish community or teenagers (just to give two examples), who mix with each other more than people outside their group. However, homogeneous mixing is a standard assumption to make the mathematics tractable.
- 群体的均匀混合,即受到仔细检查且每个个体随机分配并进行接触的群体,并且其大多不在较小的亚组中混合。 由于社会结构多种多样,因此这种假设很少成立。 例如,伦敦的大多数人只与其他是伦敦人的人接触。 此外在伦敦,则有较小的子群体,例如土耳其社区或青少年(仅举两个例子),他们的交往比其他人更多。 但是不管怎样,均匀混合假设是更易于数学上的处理分析的标准假设。
流行病模型的类型 Types of epidemic models
随机性 Stochastic
"Stochastic" means being or having a random variable. A stochastic model is a tool for estimating probability distributions of potential outcomes by allowing for random variation in one or more inputs over time. Stochastic models depend on the chance variations in risk of exposure, disease and other illness dynamics.
“随机”是指是或具有一个随机变量。 随机模型是用来估计潜在结果的概率分布的一种工具,它允许一个或多个随时间变化的随机变量的输入。 随机模型依赖于暴露风险,疾病和其他疾病动态的机会变化。
确定性 Deterministic
When dealing with large populations, as in the case of tuberculosis, deterministic or compartmental mathematical models are often used. In a deterministic model, individuals in the population are assigned to different subgroups or compartments, each representing a specific stage of the epidemic.
在处理大量人群时,例如在结核病中,经常使用确定性或仓室模型。 在确定性模型中,人群中的个体被分配到不同的亚团体或不同仓室中,每个亚团体或仓室代表流行病的一个特定阶段。
The transition rates from one class to another are mathematically expressed as derivatives, hence the model is formulated using differential equations. While building such models, it must be assumed that the population size in a compartment is differentiable with respect to time and that the epidemic process is deterministic. In other words, the changes in population of a compartment can be calculated using only the history that was used to develop the model.[6]
从一类状态转变为另一类状态的转变速率在数学上可以用导数表示,因此可以使用微分方程来建立模型。在建立这样的模型时,必须假设仓室的人口规模在时间上是可区分的,并且流行过程是确定性的。 换句话说,只能使用用于建立模型的历史记录来计算仓室的人口变化。
流行病模型 Epidemic models
Generally, people are divided into different compartments in the epidemic models, individuals in the same compartment are assigned with the same state. The most common states used are: (i) S: the susceptible state; (ii) I: the infected state; (iii) R: the recovered state. Different combinations of these states can result in different models, such as SI, SIS and SIR model.
在经典的流行病传播模型中,人们通常被划分为几种的状态。 最常见的状态是:(i)S(Susceptible):易感状态,表示处于该状态的人们处于疾病易感的状态,可以被感染; (ii)I(Infected):受感染状态;(iii) R (Recoverd):已恢复状态。这些状态的不同组合可以导致不同的模型,例如SI,SIS和SIR模型。
Herein we first consider these epidemic models in a well-mixed population.
在这里,我们首先考虑在均匀混合的人群中的这些流行病模型。
SI模型
The simplest case is the SI model, in which two states are considered, S and I. Denote s(t) and i(t) as the proportion of susceptible and infected individuals at time t, thus we have $s(t)+i(t)=1$. Suppose the probability of infected individuals infecting the susceptible individuals is $\beta$. Therefore, the SI model can be illustrated by ordinary differential equations as follows:
最简单的情况是SI模型,其中考虑了两个状态,即S和I。将s(t)和i(t)表示为在时刻t处易感染个体和受感染个体的比例,因此我们具有$s(t)+i(t)=1$。假定受感染个体I感染易感染个体S的速率为$\beta$。 在SI模型中,当一位易感态个体一旦被感染,则其将永远处于感染状态。因此,SI模型可以用以下常微分方程表示: \begin{equation} \label{eq:si} \left\{ \begin{aligned} &\frac{ds(t)}{dt}=-\beta s(t)i(t),\\ &\frac{di(t)}{dt}=\beta s(t)i(t). \end{aligned} \right. \end{equation}
SIS模型
The SIS model is used to characterize epidemics that have transient immunity, such as influenza. When it turns to the information process, it means that the individuals know about the information (in I state) will ignore the information and become susceptible again (in S state). We denote s(t) and i(t) as the fraction of susceptible and infected individuals in the population respectively. The transmission probability between I state individuals and S state individuals is $\beta$, and the recovered probability of the I state individuals is $\gamma$. Accordingly, the SIS model can also be expressed by the ordinary differential equations:
在SIS模型里,人群被划分为两类:易感人群(S)和受感染人群(I)。受感染人群为传染的源头,它通过一定速率$\beta$将疾病传播给易感人群。受感染人群本身则以速率$\gamma$被治愈恢复为易感态;易感人群一旦被感染,就又成为了新的传染源。若将此模型用于信息传播过程中,则表示尚未知晓信息的个体(S)在对信息的了解后(变为I状态),经过一段后,将忽略该信息并再次对该信息变得敏感(处于S状态)。我们将s(t)和i(t)分别表示为人群中易感和受感染个体的比例。因此,SIS模型也可以用常微分方程表示: \begin{equation} \label{eq:sis} \left\{ \begin{aligned} &\frac{ds(t)}{dt}=-\beta s(t)i(t)+\gamma i(t),\\ &\frac{di(t)}{dt}=\beta s(t)i(t)-\gamma i(t). \end{aligned} \right. \end{equation} Given an initial value i(0), we can derive the expression of i(t):
给定初始值i(0),我们可以得出i(t)的表达式: \begin{equation} \label{eq:it} i(t)=\frac{i(0)(\beta-\gamma)e^{(\beta-\gamma)t}}{\beta-\gamma+\beta i(0)e^{(\beta-\gamma)t}}. \end{equation}
We define $\lambda=\beta/\gamma$ as the effective infection rate of this model. From the above equation, we can find that when $\lambda>1$, the steady-state value of I is $i=(\beta-\gamma)/\beta=1-1/\lambda$, an endemic disease state is obtained in this case (indicates that there will be a number of infected individuals in the population at the final state). However, when $\lambda<1$, we have$i\to0(t\to\infty)$, which means that there will be no I state individuals in the population finally and is called a healthy state. Therefore, $\lambda=1$ is a threshold value of the SIS model, which is also known as the basic reproduction number.[12]
在这里,我们将$\lambda=\beta/\gamma$定义为该模型的有效感染率。 从上式可知,当$\lambda>1$时,I的稳态值为$i=(\beta-\gamma)/\beta=1-1/\lambda$,表明终态时人群中存在一定比例的受感染者,也就是说当$\lambda>1$时,整体人群处于地方性疾病状态。 但是,当$\lambda<1$时,我们有$i\to0(t\to\infty)$,这意味着最终人群中将没有I状态个体,整体人群被称为健康状态。 综上,$\lambda=1$是SIS模型的传播阈值,也称为基本再生数。
SIR模型
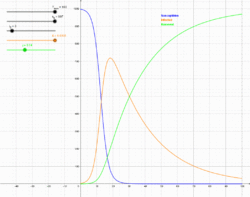
The SIR model is introduced to explain the epidemics with permanent immunity in the population. Different from the SI and SIS model, a recovered state (R) is given in this model. Individuals in S state would be infected by the I state individuals with probability $\beta$, whereas the I state individuals would recover to R state with a recovery probability $\gamma$. Thus, the ordinary differential equations of SIR model are
SIR模型是用来解释具有永久免疫力的人群中的流行病。 与SI和SIS模型不同,此模型中还存在恢复状态(R)。 处于S状态的个体被I状态个体以速率$\beta$感染,而处于I状态的个体以恢复速率$\gamma$恢复到R状态,节点一旦成为恢复的R状态则成为永久免疫人群,不可以再被感染。 因此,SIR模型的常微分方程为 \begin{equation} \label{eq:sir} \left\{ \begin{aligned} &\frac{ds(t)}{dt}=-\beta s(t)i(t),\\ &\frac{di(t)}{dt}=\beta s(t)i(t)-\gamma i(t),\\ &\frac{dr(t)}{dt}=\gamma i(t). \end{aligned} \right. \end{equation}
$\lambda=\beta/\gamma$ can also be defined as the basic reproduction number of the SIR model. We can get similar conclusion as the SIS model, i.e., when $\lambda<1$时, $r=0$, indicating that information cannot spread in the population. When $\lambda>1$, we have $r>0$, which means the information can spread out as the increase of $\lambda$. As a consequence, $\lambda=1$ is a threshold value of SIR model.
同样也可以定义$\lambda=\beta/\gamma$为该模型的有效感染率,可以得到与SIS模型类似的结论,即当$\lambda<1$时,$r=0$,表明疾病无法在人群中传播。当$\lambda>1$时,有$r>0$。$\lambda=1$是SIR模型的传播阈值。
参考文献 References
- ↑ 1.0 1.1 Epidemic Modeling: An Introduction.. New York: Cambridge University Press. 2005.
- ↑ Hethcote HW (2000). "The mathematics of infectious diseases". Society for Industrial and Applied Mathematics. 42: 599–653.
- ↑ Blower S, Bernoulli D (2004). "An attempt at a new analysis of the mortality caused by smallpox and of the advantages of inoculation to prevent it. 1766". Reviews in Medical Virology. 14 (5): 275–88. doi:10.1002/rmv.443. PMID 15334536.
- ↑ Epidemiology Old and New. London: Kegan Paul. 1928.
- ↑ Ross, Ronald (1910). The Prevention of Malaria. http://catalog.hathitrust.org/Record/001587831.
- ↑ 6.0 6.1 Mathematical Models in Population Biology and Epidemiology.. New York: Springer. 2001.
- ↑ Eisinger D, Thulke HH (April 2008). "Spatial pattern formation facilitates eradication of infectious diseases". The Journal of Applied Ecology. 45 (2): 415–423. doi:10.1111/j.1365-2664.2007.01439.x. PMC 2326892. PMID 18784795.
- ↑ Adam D (April 2020). "Special report: The simulations driving the world's response to COVID-19". Nature. 580 (7803): 316–318. doi:10.1038/d41586-020-01003-6. PMID 32242115.
- ↑ Squazzoni F, Polhill JG, Edmonds B, Ahrweiler P, Antosz P, Scholz G, et al. (2020). "Computational Models That Matter During a Global Pandemic Outbreak: A Call to Action". Journal of Artificial Societies and Social Simulation. 23 (2): 10. ISSN 1460-7425.
- ↑ Sridhar D, Majumder MS (April 2020). "Modelling the pandemic". Bmj. 369: m1567. doi:10.1136/bmj.m1567. PMID 32317328.
- ↑ Maziarz M, Zach M (October 2020). "Agent-based modelling for SARS-CoV-2 epidemic prediction and intervention assessment: A methodological appraisal". Journal of Evaluation in Clinical Practice. 26 (5): 1352–1360. doi:10.1111/jep.13459. PMC 7461315. PMID 32820573.
- ↑ Heffernan J M, Smith R J, Wahl L M. Perspectives on the basic reproductive ratio[J]. Journal of the Royal Society Interface, 2005, 2(4): 281-293.
此页参考来源:
(1)维基百科:Mathematical modelling of infectious disease
(2)Zhang Z K, Liu C, Zhan X X, et al. Dynamics of information diffusion and its applications on complex networks[J]. Physics Reports, 2016, 651: 1-34.
