基于可逆性的因果涌现理论

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
（重定向自动力学可逆性）
跳到导航 跳到搜索

基于可逆性的因果涌现理论是一种量化因果涌现的新框架，该方法基于奇异值分解，提出了近似动力学可逆性（[math]\displaystyle{ \Gamma_{\alpha} }[/math]）的概念，用于量化马尔科夫动力学接近可逆动力学的程度；与此同时，还提出了一种不经过粗粒化就能直接判断因果涌现是否发生的方法。经过理论推导和数值实验证明，在对因果涌现的判断和量化上，基于近似可逆性指标的因果涌现与Erik Hoel等人提出的基于有效信息（EI）指标的因果涌现判断具有类似的效果，且[math]\displaystyle{ \Gamma_{\alpha} }[/math]和EI在多个方面存在联系。此外，该理论还提出了基于奇异值分解（SVD）的新粗粒化策略，并通过实验证明了该方法的有效性。

简介

因果涌现（causal emergence）是指动力系统中的一类特殊的涌现现象，即系统在宏观尺度会展现出更强的因果特性。特别的，对于一类马尔科夫动力系统来说，在对其状态空间进行适当的粗粒化以后，所形成的宏观动力学会展现出比微观更强的因果特性，那么称该系统发生了因果涌现[1][2]。2013年，Hoel等人[1]最早提出了因果涌现理论，该理论利用因果效应度量来量化复杂系统中的涌现现象，该方法使用有效信息（Effective Information，简称EI）来量化系统动力学的因果性强弱。此外，2020年，Rosas等[3]从信息理论视角出发，提出一种基于信息分解方法来定义系统中的因果涌现，基于协同信息或者冗余信息来定量的刻画涌现。2023年，Barnett等人[4]基于转移熵，通过判断宏观动力学与微观动力学进行解耦来判断涌现的发生，将涌现刻画为，宏观的变量与微观的变量相互独立，没有因果关系，这也可以看做是一种因果涌现现象。

然而，现有的因果涌现理论存在着一定的局限性。例如，基于有效信息的因果涌现理论是一个依赖于粗粒化方案的理论，不同的粗粒化策略会得到完全不同的因果涌现判断。尽管这一局限可以通过最大化有效信息[5]选取粗粒化策略得到一定程度的解决，但是该优化问题还是很难求解。Rosas等人提出了用协同信息量化涌现的方法[3]，但是这种计算涉及到多个变量的所有组合，因而计算量会呈现指数增长。Rosas进一步提出了近似计算方案，但是该方与Erik Hoel的因果涌现理论一样，需要事先指定粗粒化方案及其涌现变量[3]。同样地，Seth等人的量化涌现理论也需要在粗粒化方案给定的情况下展开讨论[4]。对于粗粒化方案的过分依赖会使得这些量化涌现理论在不同程度上依赖于观察者的粗粒化策略，因而带有一定的主观色彩。那么，是否存在着一种不依赖于粗粒化方案的因果涌现理论呢？

2024年，张江等人[6]基于奇异值分解，提出了一套新的因果涌现理论。该理论的核心思想是指出所谓的因果涌现其实等价于动力学可逆性的涌现。给定一个系统的马尔科夫转移矩阵，通过对它进行奇异值分解，将奇异值的[math]\displaystyle{ \alpha }[/math]次方的和定义为马尔科夫动力学的可逆性度量（[math]\displaystyle{ \Gamma_{\alpha}\equiv \sum_{i=1}^N\sigma_i^{\alpha} }[/math]），这里[math]\sigma_i[/math]为奇异值。该指标与有效信息具有高度的相关性，也可以用于刻画动力学的因果效应强度。根据奇异值的谱，该方法可以在不显式定义粗粒化方案的条件下，直接定义所谓清晰涌现（clear emergence）和模糊涌现（vague emergence）的概念。

基于可逆性的因果涌现理论与已有的其他因果涌现理论最大的区别就是不需要指定粗粒化策略，仅从马尔科夫转移矩阵的奇异值谱就能判断因果涌现的发生，有效规避了观察者效应的问题和最大化有效信息的难以优化求解的问题。

基本概念

下面详细介绍该理论的基本概念，分别是动力学可逆性、近似动力学可逆性、清晰因果涌现和模糊因果涌现。

动力学可逆性

对于给定的马尔可夫链[math]\displaystyle{ \chi }[/math]和对应的转移概率矩阵(TPM) P ，如果P同时满足：

  1. P是可逆矩阵，即存在矩阵[math]\displaystyle{ P^{-1} }[/math]，使得[math]\displaystyle{ PP^{-1}=I }[/math]，[math]I[/math]为单位矩阵；
  2. [math]\displaystyle{ P^{-1} }[/math]也是另一个马尔可夫链[math]\displaystyle{ \chi^{-1} }[/math]的有效TPM，

则[math]\displaystyle{ \chi }[/math]和P可以称为严格动力学可逆的。

关于动力学可逆性，我们有如下定理：

定理1：对于一个给定的马尔科夫链[math]\displaystyle{ \chi }[/math]和对应的TPM P，当且仅当P是置换矩阵(Permutation Matrix)的时候，P是严格动力学可逆的。

所谓的置换矩阵是指每一个行向量都是独热向量（one-hot vector，即只有一个元素是1，其余元素均为零的向量），每两个行向量都不相同。

纯粹的置换矩阵在所有可能的TPM中非常稀少，所以大多数的TPM并不是严格动力学可逆的。因此，需要一个指标来刻画任意一个TPM接近动力学可逆的程度。考虑P的秩为r，当且仅当r<N（N为矩阵的维数）的时候，P是不可逆的；且P越退化对应着越小的r。然而，非退化（满秩）的矩阵P并不总是动力学可逆的，因为：

  1. 尽管[math]\displaystyle{ P^{-1} }[/math]存在，[math]\displaystyle{ P^{-1} }[/math]并不一定是满足归一化条件的合法TPM（即矩阵中每个元素都大于等于0，小于等于1，且每一行满足加和为1的条件）；
  2. 如前所述，若P满足动力学可逆性，则P必为置换矩阵。

所有置换矩阵的行向量都是独热向量。这一特性可以被矩阵P的弗罗贝尼乌斯范数（Frobenius norm）刻画。事实上，当且仅当P的行向量是独热向量的时候，矩阵P的弗罗贝尼乌斯范数取最大值。因此，我们可以由矩阵P的秩r和矩阵的弗罗贝尼乌斯范数找到P的近似动力学可逆性与矩阵奇异值之间的联系。

首先，矩阵的秩可以被写作：

[math]\displaystyle{ \begin{aligned} r=\sum_{i=1}^{N}\sigma_{i}^{0} \end{aligned} }[/math]

其中[math]\displaystyle{ \sigma_{i} }[/math]是矩阵P的第i个奇异值，[math]N[/math]是马尔科夫链的状态数。

紧接着，矩阵的弗罗贝尼乌斯范数可以被写作：

[math]\displaystyle{ \begin{aligned} {||P||}_{F}^{2}=\sum_{i=1}^{N}\sigma_{i}^{2} \end{aligned} }[/math]

这也是所有奇异值的平方和。可以看出矩阵的秩和弗罗贝尼乌斯范数都与奇异值相联系。

近似动力学可逆性

由于绝大部分马尔科夫链的状态转移矩阵（TPM）都不是置换矩阵，所以我们需要一个指标来刻画一个TPM靠近可逆的置换矩阵程度的指标，这就是近似动力学可逆性。 假设马尔科夫链的TPM为P，奇异值为[math]\displaystyle{ (\sigma_{1}\ge\sigma_{2}\ge...\ge\sigma_{N}\ge0) }[/math]，那么矩阵P的[math]\displaystyle{ \alpha }[/math]阶近似动力学可逆性定义为：

[math]\displaystyle{ \begin{aligned} \Gamma_{\alpha}=\sum_{i=1}^{N}\sigma_{i}^{\alpha}\end{aligned} }[/math]

其中[math]\displaystyle{ \alpha\in(0,2) }[/math]是参数。

实际上，当[math]\displaystyle{ \alpha\ge1 }[/math]时，[math]\displaystyle{ \Gamma_{\alpha} }[/math]是P的沙滕范数（Schatten norm）；当[math]\displaystyle{ 0\lt \alpha\lt 1 }[/math]时，[math]\displaystyle{ \Gamma_{\alpha} }[/math]是P的准范数（quasinorm）[7][8][9][10]。使用这个定义来刻画近似动力学可逆性是合理的，因为完全动力学可逆性可以通过最大化[math]\displaystyle{ \Gamma_{\alpha} }[/math]来得到。


我们有如下定理：

定理2：对于任意[math]\displaystyle{ \alpha\in(0,2) }[/math]，[math]\displaystyle{ \Gamma_{\alpha} }[/math]的最大值是N，当且仅当P是置换矩阵的时候能取到该最大值。更进一步来说，可以证明，[math]\displaystyle{ \Gamma_{\alpha} }[/math]的下界可以由[math]\displaystyle{ {||P||}_{F}^{\alpha} }[/math]确定[11]。

确定性和简并性

通过调整参数[math]\displaystyle{ \alpha\in(0,2) }[/math]，可以使更好地反映P的确定性或者简并性。当[math]\displaystyle{ \alpha\to0,\Gamma_{\alpha} }[/math]收敛到P的秩，这类似于EI定义中的非简并性项，因为随着P越来越退化，r越来越小。然而，定义不允许[math]\displaystyle{ \alpha }[/math]精确为零，因为r不是P的连续函数，而且最大化秩不等于置换矩阵。同样，当[math]\displaystyle{ \alpha\to2 }[/math]时，[math]\displaystyle{ \Gamma_{\alpha} }[/math]收敛到[math]\displaystyle{ {||P||}_{F}^{2} }[/math]，但是定义不允许[math]\displaystyle{ \alpha }[/math]取2，因为[math]\displaystyle{ \Gamma_{\alpha=2} }[/math]的最大化并不意味着P是可逆的。[math]\displaystyle{ {||P||}_{F} }[/math]与EI定义中的确定性项具有可比性，因为当P具有越来越多的独热向量，P中的最大转移概率也会变得更大，意味着动力学变得更加可逆。在实践中总是取[math]\displaystyle{ \alpha=1 }[/math]来平衡[math]\displaystyle{ \Gamma }[/math]测量确定性和简并性的倾向，[math]\displaystyle{ \Gamma_{\alpha=1} }[/math]被称为核范数[10][12]。为简便，下文中将[math]\displaystyle{ \Gamma_{\alpha=1} }[/math]记作[math]\displaystyle{ \Gamma }[/math]。

归一化

[math]\displaystyle{ \Gamma_{\alpha} }[/math]受矩阵的大小影响，所以我们需要对其进行归一化，得到[math]\displaystyle{ \gamma_{\alpha} }[/math]来刻画与大小无关的近似动力学可逆性，这样可以更方便地在不同大小的马尔科夫链之间进行比较：

[math]\displaystyle{ \begin{aligned} \gamma_{\alpha}=\frac{\Gamma_{\alpha}}{N}\end{aligned} }[/math]

容易证明，[math]\displaystyle{ \gamma_{\alpha} }[/math]总是小于1。

具体例子

在下图中，作者给出了四个具体马尔科夫链的例子，该马氏链的状态转移矩阵如下图所示。我们可以对比该马氏链的[math]\displaystyle{ EI }[/math]和近似动力学可逆性（图中的[math]\displaystyle{ \Gamma }[/math]，即[math]\displaystyle{ \Gamma_{\alpha=1} }[/math]）。对比图(a)，(b)，我们发现对于不同的状态转移矩阵，[math]\displaystyle{ EI }[/math]降低的时候，[math]\displaystyle{ \Gamma }[/math]也同步降低。进一步，图(c)和(d)是对比粗粒化前后的效果，其中图(d)是对图(c)状态转移矩阵的粗粒化（将前三个状态归并为一个宏观态）。由于宏观状态转移矩阵图(d)是一个确定性系统，因此，归一化后的[math]\displaystyle{ EI }[/math]，[math]\displaystyle{ eff\equiv EI/\log N }[/math]和归一化后的[math]\Gamma[/math]：[math]\displaystyle{ \gamma\equiv \Gamma/N }[/math]都达到了最大值1。

Gamma例子.png

清晰因果涌现

对于具有TPM P的给定马尔可夫链[math]\displaystyle{ \chi }[/math]，如果[math]\displaystyle{ r≡rank(P)\lt N }[/math]，则该系统中会出现明显的因果涌现。且因果涌现的程度为：

[math]\displaystyle{ \begin{aligned} \Delta\Gamma_{\alpha}=\Gamma_{\alpha}\cdot(\frac{1}{r}-\frac{1}{N}) \end{aligned} }[/math]

模糊因果涌现

对于具有TPM P的给定马尔可夫链[math]\displaystyle{ \chi }[/math]，假设其奇异值为[math]\displaystyle{ (\sigma_{1}\ge\sigma_{2}\ge...\ge\sigma_{N}\ge0) }[/math]。对于给定实值[math]\displaystyle{ \epsilon\in[0,\sigma_{1}] }[/math]，如果存在整数[math]\displaystyle{ i\in[1, N) }[/math]，使得[math]\displaystyle{ \sigma_{i}\gt \epsilon }[/math]，则系统中出现了模糊因果涌现，其模糊程度为[math]\displaystyle{ \epsilon }[/math]。而因果涌现的程度为：

[math]\displaystyle{ \begin{aligned} \Delta\Gamma_{\alpha}(\epsilon)=\frac{\sum_{i=1}^{r_{\epsilon}}\sigma_{i}^{\alpha}}{r_{\epsilon}}-\frac{\sum_{i=1}^{N}\sigma_{i}^{\alpha}}{N}, \end{aligned} }[/math]

其中[math]\displaystyle{ r_{\epsilon}=max\{ i| \sigma_{i} \gt \epsilon\} }[/math]

这些定义与任何粗粒化方法无关，它代表了马尔可夫动力学的内在客观属性。因此，清晰和模糊因果涌现的程度都可以客观地量化。当[math]\displaystyle{ \epsilon=0 }[/math]时，清晰因果涌现是模糊因果涌现的特例，特别是当奇异值可以分析求解时，它具有理论价值。此外，对因果涌现发生的判断与[math]\displaystyle{ \alpha }[/math]无关，因为它只与秩有关。因此，清晰因果涌现的概念仅由P决定，是无参数的。在实际应用中，必须给出阈值[math]\displaystyle{ \epsilon }[/math]，因为奇异值可能无限趋近于0，但P是满秩的。可以根据奇异值频谱中的明显截止点来选择[math]\displaystyle{ \epsilon }[/math]。若[math]\displaystyle{ \epsilon }[/math]非常小（比如[math]\displaystyle{ \epsilon\lt {10}^{-10} }[/math]），我们也可以说因果涌现大致发生。对于任意[math]\displaystyle{ \epsilon\ge{0},\Delta\Gamma_{\alpha}(\epsilon)\in[0,N-1] }[/math]，只有当[math]\displaystyle{ \Delta\Gamma_{\alpha}(\epsilon)\gt 0 }[/math]时，才会出现因果涌现。

与有效信息（EI）的比较

定理3：对于任意 TPM P 和 [math]\displaystyle{ \alpha\in(0,2) }[/math]，[math]\displaystyle{ \Gamma_{\alpha} }[/math]的对数和EI都有相同的最小值0和一个共同的极小值点（当[math]\displaystyle{ P=\frac{1}{N} \mathbb{1}_{N\times{N}} }[/math]时取到），其中[math]\displaystyle{ \mathbb{1} }[/math]是全1矩阵。它们还有相同的最大值[math]\displaystyle{ \log{N} }[/math]，最大值点对应于P是一个置换矩阵。

因此当P是可逆的（置换矩阵）时，[math]\displaystyle{ \log{\Gamma_{\alpha}} }[/math]和EI可以达到最大值[math]\displaystyle{ \log{N} }[/math]。当[math]\displaystyle{ P_{i}=\frac{\mathbb{1}}{N},\forall{i}\in[1,N] }[/math]，它们也可以达到最小值0。然而，我们可以证明[math]\displaystyle{ \frac{\mathbb{1}}{N} }[/math]并不是EI的唯一最小点，对于任何满足[math]\displaystyle{ P_{i}=P_{j},\forall{i}\in{[1,N]} }[/math]的TPM都能使EI=0。其次EI的上限和下限都是[math]\displaystyle{ \log{\Gamma_{\alpha}} }[/math]的线性项。


定理4：对于任何TPM P，其有效信息EI的上限为[math]\displaystyle{ \frac{2}{\alpha}\log{\Gamma_{\alpha}} }[/math]，下限为[math]\displaystyle{ \log{\Gamma_{\alpha}}-\log{N} }[/math].

因此，有如下不等式：

[math]\displaystyle{ \begin{aligned} \log{\Gamma_{\alpha}}-\log{N}\le{EI}\le\frac{2}{\alpha}\log{\Gamma_{\alpha}} \end{aligned} }[/math]

实际上，EI有一个更严格的上限，[math]\displaystyle{ EI\le\log{\Gamma_{\alpha}} }[/math]，这个上限是由数值实验的结果确定的。我们发现在许多例子中，EI和[math]\displaystyle{ \log\Gamma_{\alpha} }[/math]具有近似线性关系，因此，基于可逆性的因果涌现理论主张：

[math]\displaystyle{ \begin{aligned} EI\sim\log\Gamma_{\alpha}. \end{aligned} }[/math]

相似性

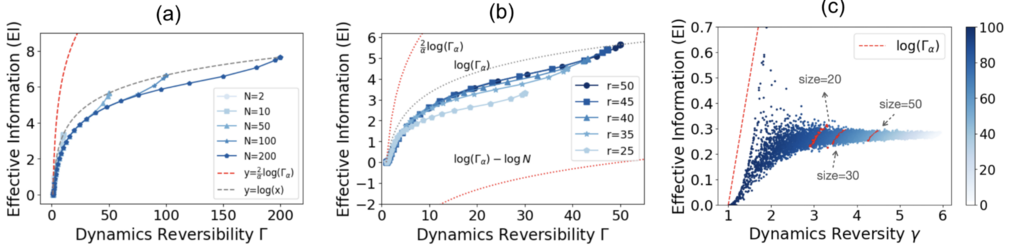
根据前文，EI的上界和下界分别是[math]\displaystyle{ \log{\Gamma_{\alpha}} }[/math]的线性项。由此还可以推测两者具有近似关系：[math]\displaystyle{ EI\sim\log{\Gamma_{\alpha}} }[/math]。下面通过数值模拟说明这一点。

如下图所示，在由三种不同方法生成的各种归一化的TPM 上比较了[math]\displaystyle{ \log{\Gamma_{\alpha}} }[/math]和 EI：1）软化置换矩阵；2）软化退化矩阵；3）完全随机矩阵。以下是具体生成步骤：

软化置换矩阵：

1）随机生成一个N阶置换矩阵P；

2）对于P中的每个行向量[math]\displaystyle{ P_{i} }[/math]，假设1元素的位置是[math]\displaystyle{ j_{i} }[/math]，我们将[math]\displaystyle{ P_{i} }[/math]的所有条目填入位于[math]\displaystyle{ j_{i} }[/math]处的高斯分布中心的概率，即[math]\displaystyle{ P'_{i,j} = \frac{1}{\sqrt{2\pi}\sigma} \exp\left( -\frac{(j - j_i)^2}{\sigma^2} \right) }[/math]，其中，[math]\displaystyle{ \sigma }[/math]是软化程度的自由参数；

3) 将[math]\displaystyle{ \sum_{j=1}^{N} P'_{ij} = 1 }[/math]除以新的行向量，使其归一化，这样修改后的矩阵[math]\displaystyle{ P' }[/math]也是一个TPM。

软化退化矩阵：

生成方式与软化置换矩阵非常相似，但原始矩阵P不是置换矩阵，而是退化矩阵。退化意味着有一些行向量是相同的，相同行向量的数量用N - r表示，它是受控变量，其中r是P的秩。通过调整N-r，我们可以控制TPM的退化程度。

完全随机矩阵：

1) 从[0, 1]上的均匀分布中抽取一个行随机向量；

2) 对该行向量进行归一化处理，使生成的矩阵是一个TPM。


图(a)、(b)和(c)表明，在这些例子中都观察到了正相关性，并且在N ≫ 1 时，[math]\displaystyle{ EI\sim\log{\Gamma_{\alpha}}. }[/math]的近似关系得到了证实。在(a) 和 (b) 中可以明显观察到这种关系，但在(b) 中，由于覆盖了有限的[math]\displaystyle{ \Gamma }[/math]值区域，这种关系退化为近似线性关系。

图(a)和(b)中用红色虚线表示了 EI 的上下限。不过，在图(c）中，由于所有点都集中在一个小区域内，因此看不到理论边界线。根据经验，图中灰色断线所示的[math]\displaystyle{ \log{\Gamma_{\alpha}} }[/math]的上限更为严格。因此可以推测 [math]\displaystyle{ EI\le\log{\Gamma_{\alpha}} }[/math]这一新关系是成立的，但其严密性有待证明。

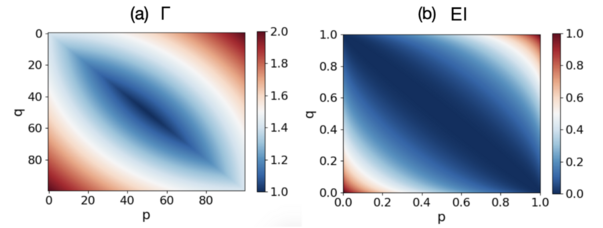
文献中作者还在大小为N=2 的最简单参数化TPM中得到了EI和[math]\displaystyle{ \Gamma }[/math]的解析解，并展示了EI和[math]\displaystyle{ \Gamma }[/math]与参数p和q的关系。其中p和q用于生成最简单的[math]\displaystyle{ 2 \times 2 }[/math]马尔科夫矩阵[math]\displaystyle{ P=\begin{pmatrix} p& 1-p\\ 1-q & q \end{pmatrix} }[/math]，下图(a)表示[math]\displaystyle{ \Gamma }[/math]随p和q的变化，图(b)表示EI随p和q 的变化。(a)和(b)之间的差异显而易见：1）当[math]\displaystyle{ p\approx 1-q }[/math]时，[math]\displaystyle{ \Gamma }[/math]有一个峰值，但EI没有；2）观察到EI ≈ 0时的区域更宽，而[math]\displaystyle{ \Gamma\approx 1 }[/math]时的区域要小得多；3）观察到[math]\displaystyle{ \Gamma }[/math]有一个从0到最大N=2的渐进过渡，但EI没有。 因此，我们得出结论，EI和[math]\displaystyle{ \Gamma }[/math]在各种TPM上高度相关。

不同

首先，EI 通过KL散度来量化每个行向量与P的平均行向量之间的差异，衡量的是行向量之间的相似性。相反，[math]\displaystyle{ \Gamma_{\alpha} }[/math]评估的是动力学可逆性，特别是当[math]\displaystyle{ \alpha }[/math]接近 0 时，这与行向量之间的线性相互依赖性相关。虽然行向量的线性相互依赖性表明它们的相似性——这意味着两个相同的行向量是线性相关的，但反之则不一定成立。因此，[math]\displaystyle{ \Gamma_{\alpha} }[/math]不仅捕获了行向量之间的相似性，而且还捕获了P与动力学可逆矩阵的接近度。相比之下，EI无法完成这个任务。

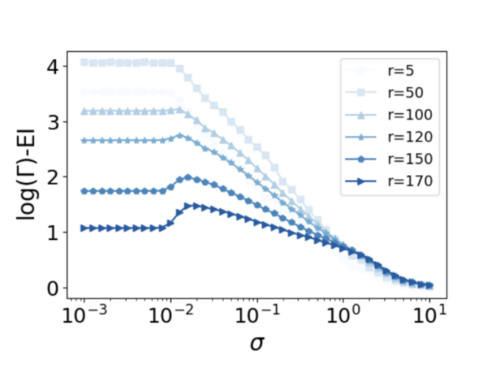
可以通过以下数值实验来验证这一点：可以通过将线性相关行向量与线性独立行向量混合来创建TPM，其中独立向量的数量或等级是受控参数。首先，生成r个独立的独热向量，然后软化这些行向量，软化程度由[math]\displaystyle{ \sigma }[/math]确定。随后，通过将这些软化的独热向量与随机选择的线性系数线性组合来创建额外的行向量。然后量化[math]\displaystyle{ \Gamma }[/math]和 EI 之间的差异，结果如下图所示。

很明显，对于较小的r值，随着[math]\displaystyle{ \sigma }[/math]的增加，[math]\displaystyle{ \log{\Gamma} }[/math]和 EI 之间的差异会减小，因为 P 的线性依赖性随着向量变得更加明显而增强。这强调了线性相关性并不等于行向量之间的相似性。然而，随着独立行向量数量的增加，如果[math]\displaystyle{ \sigma }[/math]保持很小，P会收敛到置换矩阵。因此，EI 和[math]\displaystyle{ \log{\Gamma} }[/math]都达到相同的最大值。这解释了为什么当r很大时会出现轻微的颠簸。

其次，即使在所有行向量相同的情况下，EI 和[math]\displaystyle{ \Gamma_{\alpha} }[/math]之间也存在显着区别，导致 EI= 0 而[math]\displaystyle{ \Gamma_{\alpha}= ||\overline{P}||^{\alpha}\cdot N^{\alpha /2} }[/math]，而这是一个可以随[math]\displaystyle{ ||\overline{P}|| }[/math]变化的量。这种差异意味着，与 EI 不同，[math]\displaystyle{ \Gamma_{\alpha} }[/math]可以提供有关行向量的更全面的见解，超越其与平均行向量的相似性。

基于SVD分解的新粗粒化策略

虽然无需粗粒化也能定义和量化清晰或模糊因果涌现，但需要对原始系统进行更简单的粗粒化描述，以便与 EI 得出的结果进行比较。因此，该理论提供了一种基于奇异值分解的粗粒化方法，以获得宏观层面的简化TPM。其基本思想是将 P 中的行向量 [math]\displaystyle{ P_{i},\forall i \in [1,N] }[/math]投影到[math]\displaystyle{ P\cdot P^{T} }[/math]的特征向量张成的子空间上，从而保留P的主要信息，并保持[math]\displaystyle{ \Gamma }[/math]不变。

方法

该方法的基本思路是将P中的所有行向量[math]\displaystyle{ P_{i} }[/math]视为维数为N的数据向量，然后首先对这些行向量进行PCA降维，其次将其聚类为r个簇，其中r是根据奇异值频谱的阈值[math]\displaystyle{ \epsilon }[/math]选取的。有了聚类，我们就可以根据所有平稳流都是保守的原则，对原始TPM进行粗粒化。

1) 对P进行SVD分解（假设P是不可归约的，且具有周期性，从而存在平稳分布）：

[math]\displaystyle{ P=U\cdot \Sigma \cdot V^{T}, }[/math]

其中，[math]\displaystyle{ U }[/math]和[math]\displaystyle{ V }[/math]是两个尺寸为N×N的正交归一化矩阵，[math]\displaystyle{ \Sigma = diag(\sigma_{1},\sigma_{2},...,\sigma_{N}) }[/math] 是一个对角矩阵，包含所有有序奇异值。

2)选择一个[math]\displaystyle{ \epsilon }[/math]作为阈值来切断奇异值谱，并得到[math]\displaystyle{ r_{\epsilon} }[/math]作为保留状态的个数；

3)通过计算[math]\displaystyle{ \tilde{P}\equiv P\cdot V_{N\times r_{\epsilon}} }[/math]对P中的所有[math]\displaystyle{ P_{i} }[/math]进行降维，其中[math]\displaystyle{ V_{N\times r_{\epsilon}} }[/math]由[math]\displaystyle{ P\cdot P^{T} }[/math]的前[math]\displaystyle{ r_{\epsilon} }[/math]特征向量构成；

4) 通过 K-means 算法将[math]\displaystyle{ \tilde{P} }[/math]中的所有行向量聚类为r组，得到投影矩阵[math]\displaystyle{ \Phi }[/math]，其定义为:

[math]\displaystyle{ \Phi_{ij} =\begin{cases} 1, & \text{如果}\tilde{P_{i}}\text{属于第r组}\\ 0, & \text{其他情况} \end{cases} }[/math]

对[math]\displaystyle{ \forall i,j \in [1,N] }[/math]都成立。

5) 利用[math]\displaystyle{ \Phi }[/math]和P得到新的TPM。

为了说明如何获得简化的TPM，首先定义一个矩阵，称为平稳流矩阵，如下所示：

[math]\displaystyle{ F_{ij} \equiv \mu_i \cdot P_{ij}, \, \forall i,j \in [1, N], }[/math]

其中，[math]\displaystyle{ \mu }[/math]是P的平稳分布，满足[math]\displaystyle{ P\cdot\mu=\mu }[/math]。

其次，我们将根据 [math]\displaystyle{ \Phi }[/math]和[math]\displaystyle{ F }[/math]推导出简化平稳流矩阵：

[math]\displaystyle{ F' = \Phi^T \cdot F \cdot \Phi, }[/math]

其中，F'是简化平稳流矩阵。最后，粗粒化后的TPM可直接通过以下公式得出：

[math]\displaystyle{ P'_i = F'_i / \sum_{j=1}^{N} (F'_i)_j, \, \forall i \in [1, N]. }[/math]

测试量化因果涌现的效果

布尔网络

下面基于Hoel等人的论文[13][14]中提出的几种布尔网络马尔可夫动力学来测试清晰和模糊因果涌现的定义。

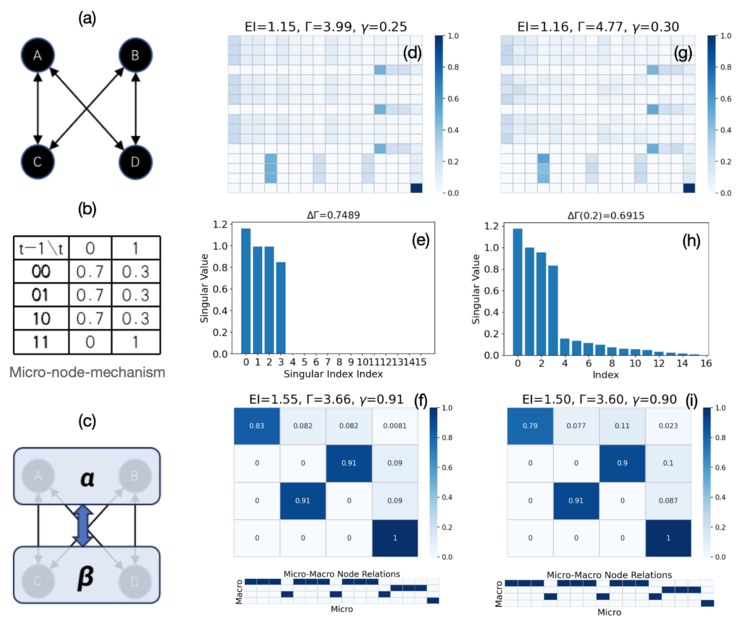
下图(a)-(i)分别显示了从具有相同节点机制的相同布尔网络模型生成的用于清晰因果涌现和模糊因果涌现的TPM的两个示例。图(c) 表示通过粗粒化(a)得到的新布尔网络，粗粒化策略是从 (f) 和 (i) 的 TPM 中提取的。图(d)中的TPM直接源自图(a)和(b)中的布尔网络及其节点机制。它们的奇异值谱分别如图(e)和(h)所示。(d)中的例子只有4个非零奇异值，奇异频谱如图(e)所示，因此，出现明显的因果涌现，且因果涌现的程度为[math]\displaystyle{ \Delta\Gamma=0.75 }[/math]。 因果涌现的判断与参考文献[13]相同。(f) 和 (i) 分别是对 (d) 和 (g) 中的原始 TPM 应用粗粒化方法后缩减的TPM和投影矩阵。

图(g)中的TPM可以显示出模糊的因果涌现，这是在(d)中的TPM上添加强度为（std = 0.03）的随机高斯噪声后得到的。因此，奇异频谱如图(h)所示。我们选择[math]\displaystyle{ \epsilon=0.2 }[/math]作为阈值，这样就只剩下4个大的奇异值。因果涌现程度为[math]\displaystyle{ \Delta\Gamma(0.2)=0.69 }[/math]。[math]\displaystyle{ \epsilon }[/math]值是根据图(h)中的奇异值频谱选择的，在图(h)中可以观察到指数为3和[math]\displaystyle{ \epsilon=0.2 }[/math]时有一个明显的分界点。

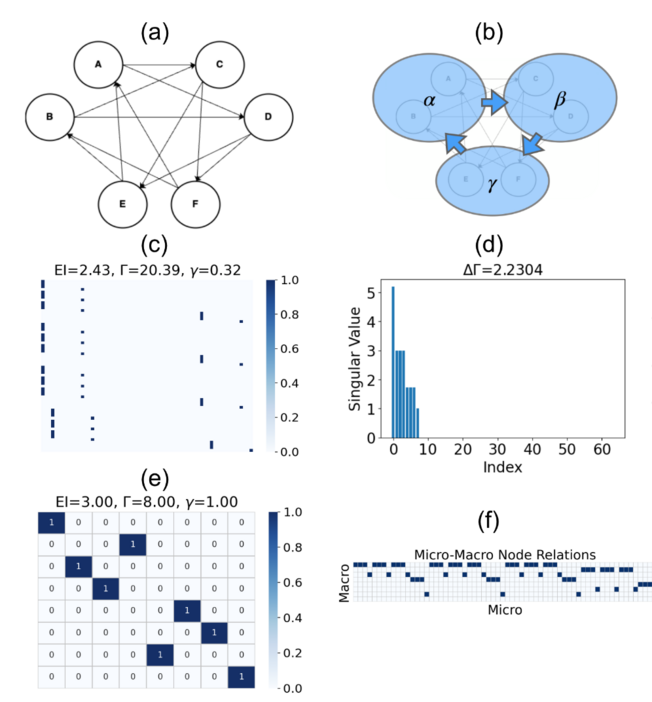
下图显示了另一个更复杂的布尔网络模型的明显因果涌现例子，该模型来自参考文献[13]，其中具有相同节点机制的6个节点可归类为3个超级节点，以显示因果涌现。(a)为6节点12边的布尔网络模型。 (b)是根据(e)中的TPM得出的粗粒化后的布尔网络模型。原始布尔网络模型的相应TPM如图(c)所示。奇异值频谱如图(d）所示，其中有8个非零值。这个清晰因果涌现的程度为[math]\displaystyle{ \Delta\Gamma=2.23 }[/math]。对因果涌现的判断与[13]相同。(e) 是对(c)的粗粒化。(f) 是根据基于 SVD 的粗粒化方法得到的从微观状态到宏观状态的投影矩阵。

复杂网络

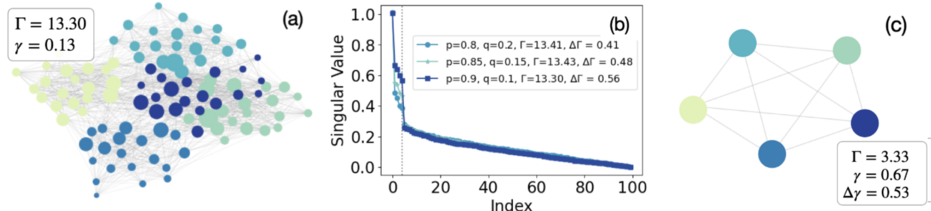
对因果涌现的量化可应用于复杂网络，如下图所示。图（a)-(c）显示了由随机块模型（SBM）生成的具有三组参数（内部连接概率）的复杂网络的模糊因果涌现例子。TPM是通过对网络的邻接矩阵按每个节点的度进行归一化得到的。图(a)显示了一个有 100 个节点和 5 个区块（社区）的示例网络，图(b)显示了其奇异值频谱，同图中还显示了另外两个由SBM生成的网络光谱，它们的大小和块数相同，但参数不同。图(c) 是利用基于SVD的粗粒化方法进行缩减后的 (a) 网络。图(b)中，在与区块数相同的横坐标上可以观察到一个明显的分界点[math]\displaystyle{ (\epsilon=0.3,r_{\epsilon}=5) }[/math]。可以确定，在这个网络模型中出现了模糊的因果涌现，程度为[math]\displaystyle{ \Delta\Gamma(0.3)=0.56 }[/math]。

元胞自动机

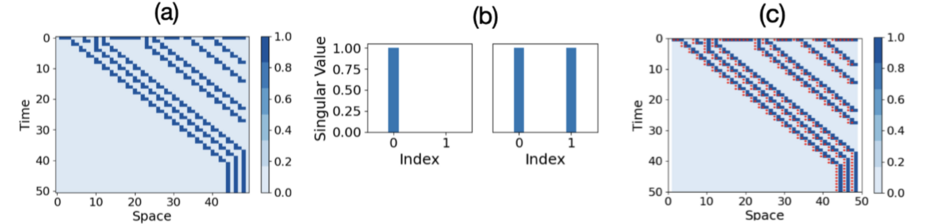
如下图所示，关于清晰因果涌现的定义可应用于元胞自动机，以发现其局部涌现结构。在这个例子里刻画了元胞自动机（编号40的基本一维元胞自动机）局部TPM的清晰因果涌现。(a)是第40号元胞自动机的演化（规则是：000 → 0, 001 → 0, 010 → 1, 011 → 0, 100 → 1, 101 → 0, 110 → 0, 111 → 0）。局部TPM 由包括每个单元及其两个相邻单元的局部窗口获得。图(b) 显示了这些局部 TPM 的奇异值的可能频谱，在这些频谱中可能出现也可能不出现清晰因果涌现。图(c)用红点标记显示了所有单元和时间步长的清晰因果涌现分布（[math]\displaystyle{ \Delta\Gamma }[/math]）。

参考文献

  1. ↑ 1.0 1.1 Hoel E P, Albantakis L, Tononi G. Quantifying causal emergence shows that macro can beat micro[J]. Proceedings of the National Academy of Sciences, 2013, 110(49): 19790-19795.
  2. ↑ Hoel E P. When the map is better than the territory[J]. Entropy, 2017, 19(5): 188.
  3. ↑ 3.0 3.1 3.2 Rosas F E, Mediano P A, Jensen H J, et al. Reconciling emergences: An information-theoretic approach to identify causal emergence in multivariate data[J]. PLoS computational biology, 2020, 16(12): e1008289.
  4. ↑ 4.0 4.1 Barnett L, Seth AK. Dynamical independence: discovering emergent macroscopic processes in complex dynamical systems. Physical Review E. 2023 Jul;108(1):014304.
  5. ↑ Mingzhe Yang, Zhipeng Wang, Kaiwei Liu, et al. Finding emergence in data by maximizing effective information. National Science Review, 2024, nwae279
  6. ↑ Zhang J, Tao R, Yuan B. Dynamical Reversibility and A New Theory of Causal Emergence. arXiv preprint arXiv:2402.15054. 2024 Feb 23.
  7. ↑ Schatten norm from Wikipedia. https://en.wikipedia.org/wiki/Schatten norm
  8. ↑ Recht, B., Fazel, M., Parrilo, P.A.: Guaranteed minimum-rank solutions of linear matrix equations via nuclear norm minimization. SIAM review 52(3), 471–501 (2010)
  9. ↑ Chi, Y., Lu, Y.M., Chen, Y.: Nonconvex optimization meets low-rank matrix factorization: An overview. IEEE Transactions on Signal Processing 67(20), 52395269 (2019)
  10. ↑ 10.0 10.1 Cui, S., Wang, S., Zhuo, J., Li, L., Huang, Q., Tian, Q.: Towards discriminability and diversity: Batch nuclear-norm maximization under label insufficient situations. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 3941–3950 (2020)
  11. ↑ Zhang, Jiang, Ruyi Tao, and Bing Yuan. "Dynamical Reversibility and A New Theory of Causal Emergence." arXiv preprint arXiv:2402.15054 (2024).
  12. ↑ Fazel, M.: Matrix rank minimization with applications. PhD thesis, PhD thesis, Stanford University (2002)
  13. ↑ 13.0 13.1 13.2 13.3 Hoel, E.P., Albantakis, L., Tononi, G.: Quantifying causal emergence shows that macro can beat micro. Proceedings of the National Academy of Sciences of the United States of America 110(49), 19790–19795 (2013) https://doi.org/10.1073/ pnas.1314922110
  14. ↑ Hoel, E.P.: When the map is better than the territory. Entropy 19(5) (2017) https://doi.org/10.3390/e19050188

编者推荐

下面是一些链接能够帮助读者更好的了解因果涌现的相关信息：

因果涌现读书会

文章推荐

路径推荐

此词条由龚铭康编写，张江和王志鹏整理和审校。

本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。

取自“https://wiki.swarma.org/index.php?title=基于可逆性的因果涌现理论&oldid=39154”