团复形

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
跳到导航 跳到搜索

此词条暂由彩云小译翻译，翻译字数共1193，未经人工整理和审校，带来阅读不便，请见谅。

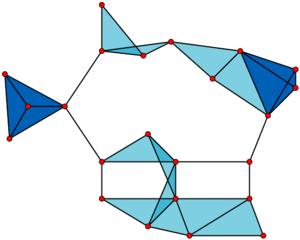
"Whitney complex" redirects here. For the Mississippi sports facility, see Davey Whitney Complex.
The clique complex of a graph. Cliques of size one are shown as small red disks; cliques of size two are shown as black line segments; cliques of size three are shown as light blue triangles; and cliques of size four are shown as dark blue tetrahedra.


thumb|300px|The clique complex of a graph. Cliques of size one are shown as small red disks; cliques of size two are shown as black line segments; cliques of size three are shown as light blue triangles; and cliques of size four are shown as dark blue tetrahedra.

图的团复数。大小为1的团体显示为小红色圆盘; 大小为2的团体显示为黑线段; 大小为3的团体显示为浅蓝色三角形; 大小为4的团体显示为深蓝色四面体。

Clique complexes, flag complexes, and conformal hypergraphs are closely related mathematical objects in graph theory and geometric topology that each describe the cliques (complete subgraphs) of an undirected graph.

Clique complexes, flag complexes, and conformal hypergraphs are closely related mathematical objects in graph theory and geometric topology that each describe the cliques (complete subgraphs) of an undirected graph.

团复合图、旗复合图和保形超图是图论和几何拓扑学中密切相关的数学对象，它们分别描述无向图的团(完全子图)。

The clique complex X(G) of an undirected graph G is an abstract simplicial complex (that is, a family of finite sets closed under the operation of taking subsets), formed by the sets of vertices in the cliques of G. Any subset of a clique is itself a clique, so this family of sets meets the requirement of an abstract simplicial complex that every subset of a set in the family should also be in the family. The clique complex can also be viewed as a topological space in which each clique of k vertices is represented by a simplex of dimension k – 1. The 1-skeleton of X(G) (also known as the underlying graph of the complex) is an undirected graph with a vertex for every 1-element set in the family and an edge for every 2-element set in the family; it is isomorphic to G.[1]

The clique complex of an undirected graph is an abstract simplicial complex (that is, a family of finite sets closed under the operation of taking subsets), formed by the sets of vertices in the cliques of . Any subset of a clique is itself a clique, so this family of sets meets the requirement of an abstract simplicial complex that every subset of a set in the family should also be in the family. The clique complex can also be viewed as a topological space in which each clique of vertices is represented by a simplex of dimension . The 1-skeleton of (also known as the underlying graph of the complex) is an undirected graph with a vertex for every 1-element set in the family and an edge for every 2-element set in the family; it is isomorphic to ..

无向图的群复合体是一个抽象的单纯复形(即，在取子集操作下闭合的有限集族) ，由图的群中的顶点集合形成。一个集团的任何子集本身就是一个集团，所以这个集合家族满足了一个抽象单纯复形的要求，即集合家族中的每个子集都应该是在家族中的。团复合体也可以看作是一个拓扑空间，其中每个顶点团都由一个维数单形表示。复数的1-骨架(也称为复数的底层图)是一个无向图，族中每一个1元素集合都有一个顶点，族中每一个2元素集合都有一个边。.

Clique complexes are also known as Whitney complexes, after Hassler Whitney. A Whitney triangulation or clean triangulation of a two-dimensional manifold is an embedding of a graph G onto the manifold in such a way that every face is a triangle and every triangle is a face. If a graph G has a Whitney triangulation, it must form a cell complex that is isomorphic to the Whitney complex of G. In this case, the complex (viewed as a topological space) is homeomorphic to the underlying manifold. A graph G has a 2-manifold clique complex, and can be embedded as a Whitney triangulation, if and only if G is locally cyclic; this means that, for every vertex v in the graph, the induced subgraph formed by the neighbors of v forms a single cycle.[2]

Clique complexes are also known as Whitney complexes, after Hassler Whitney. A Whitney triangulation or clean triangulation of a two-dimensional manifold is an embedding of a graph onto the manifold in such a way that every face is a triangle and every triangle is a face. If a graph has a Whitney triangulation, it must form a cell complex that is isomorphic to the Whitney complex of . In this case, the complex (viewed as a topological space) is homeomorphic to the underlying manifold. A graph has a 2-manifold clique complex, and can be embedded as a Whitney triangulation, if and only if is locally cyclic; this means that, for every vertex in the graph, the induced subgraph formed by the neighbors of forms a single cycle.; ; .

帮派情结也被称为惠特尼情结，以海瑟勒 · 惠特尼命名。二维流形的惠特尼三角化或干净三角化是将图嵌入到流形中，使得每个面都是一个三角形，每个三角形都是一个面。如果一个图有一个惠特尼三角形，它必须形成一个与惠特尼三角形同构的单元复合体。在这种情况下，这个复合体(被看作是一个拓扑空间)与下面的流形是同胚的。一个图有一个2-流形团复，可以嵌入为惠特尼三角形，当且仅当是局部循环的; 这意味着，对于图中的每一个顶点，由其邻居形成的诱导子图形成一个单一的循环。; ; .

The clique complex of G is equivalent to the independence complex of the complement graph of G.

The clique complex of is equivalent to the independence complex of the complement graph of .

党派情结相当于补图的独立情结。

Not every abstract simplicial complex is a clique complex. For example, consider the abstract simplicial complex over {1,2,3,4} with maximal sets {1,2,3}, {2,3,4}, {4,1}. If it were the X(G) of some graph G, then G had to have the edges {1,2}, {1,3}, {2,3}, {2,4}, {3,4}, {4,1}, so X(G) should also contain the clique {1,2,3,4}.

Not every abstract simplicial complex is a clique complex. For example, consider the abstract simplicial complex over with maximal sets If it were the of some graph , then had to have the edges so should also contain the clique

不是每个抽象的单纯复形都是小集团情结。例如，考虑抽象单纯复形的最大集合如果它是某个图的边，那么必须有边，所以也应该包含团

Flag complex

A flag complex is an abstract simplicial complex such that every set of vertices in which all pairs are faces of the complex is also itself a face of the complex. Thus, flag complexes and clique complexes are essentially the same thing. Any flag complex is the clique complex of its 1-skeleton. However, in many cases it is convenient to define a flag complex directly from some data other than a graph, rather than indirectly as the clique complex of a graph derived from that data.[3]

A flag complex is an abstract simplicial complex such that every set of vertices in which all pairs are faces of the complex is also itself a face of the complex. Thus, flag complexes and clique complexes are essentially the same thing. Any flag complex is the clique complex of its 1-skeleton. However, in many cases it is convenient to define a flag complex directly from some data other than a graph, rather than indirectly as the clique complex of a graph derived from that data..

标志复合体标志复合体是一个抽象的单纯复形，这样每一组顶点，其中所有对都是复合体的面，它本身也是复合体的面。因此，旗帜情结和派系情结本质上是一回事。任何旗帜复合体都是其1-骨架的集团复合体。然而，在许多情况下，直接从图以外的某些数据定义一个标志复合体是很方便的，而不是间接地将标志复合体定义为从该数据派生出来的图的集团复合体。.

Mikhail Gromov defined the no-Δ condition to be the condition of being a flag complex.

Mikhail Gromov defined the no-Δ condition to be the condition of being a flag complex.

Mikhail Gromov 将 no-Δ 条件定义为旗帜复合体的条件。

Conformal hypergraph

The primal graph G(H) of a hypergraph is the graph on the same vertex set that has as its edges the pairs of vertices appearing together in the same hyperedge. A hypergraph is said to be conformal if every maximal clique of its primal graph is a hyperedge, or equivalently, if every clique of its primal graph is contained in some hyperedge.[4] If the hypergraph is required to be downward-closed (so it contains all hyperedges that are contained in some hyperedge) then the hypergraph is conformal precisely when it is a flag complex. This relates the language of hypergraphs to the language of simplicial complexes.

The primal graph G(H) of a hypergraph is the graph on the same vertex set that has as its edges the pairs of vertices appearing together in the same hyperedge. A hypergraph is said to be conformal if every maximal clique of its primal graph is a hyperedge, or equivalently, if every clique of its primal graph is contained in some hyperedge.; . If the hypergraph is required to be downward-closed (so it contains all hyperedges that are contained in some hyperedge) then the hypergraph is conformal precisely when it is a flag complex. This relates the language of hypergraphs to the language of simplicial complexes.

超图的原始图 G (H)是位于同一顶点集上的图，它的边是同一超边中出现的顶点对。如果一个超图的原图的每个最大团都是超边，或者等价地，如果它的原图的每个团都包含在某个超边中，那么这个超图就是保形的。; .如果超图需要是向下闭的(因此它包含了包含在某个超边中的所有超边) ，那么当超图是一个标志复合体时，它是精确保形的。这将超图的语言与单形复合体的语言联系起来。

Examples and applications

The barycentric subdivision of any cell complex C is a flag complex having one vertex per cell of C. A collection of vertices of the barycentric subdivision form a simplex if and only if the corresponding collection of cells of C form a flag (a chain in the inclusion ordering of the cells).[3] In particular, the barycentric subdivision of a cell complex on a 2-manifold gives rise to a Whitney triangulation of the manifold.

The barycentric subdivision of any cell complex C is a flag complex having one vertex per cell of C. A collection of vertices of the barycentric subdivision form a simplex if and only if the corresponding collection of cells of C form a flag (a chain in the inclusion ordering of the cells). In particular, the barycentric subdivision of a cell complex on a 2-manifold gives rise to a Whitney triangulation of the manifold.

任何单元复合体 C 的重心细分都是一个标志复合体，每个单元 C 有一个顶点。重心细分的顶点集合形成单纯形当且仅当相应的 C 细胞集合形成一个标志(细胞包含顺序中的一个链)。特别地，细胞复合体在2-流形上的重心细分产生了流形的惠特尼三角形。

The order complex of a partially ordered set consists of the chains (totally ordered subsets) of the partial order. If every pair of some subset is itself ordered, then the whole subset is a chain, so the order complex satisfies the no-Δ condition. It may be interpreted as the clique complex of the comparability graph of the partial order.[3]

The order complex of a partially ordered set consists of the chains (totally ordered subsets) of the partial order. If every pair of some subset is itself ordered, then the whole subset is a chain, so the order complex satisfies the no-Δ condition. It may be interpreted as the clique complex of the comparability graph of the partial order.

部分序集的序复合包括部分序的链(全序子集)。如果一个子集的每一对本身都是有序的，那么整个子集就是一个链，所以有序复合体满足 no-Δ 条件。它可以解释为偏序可比图的团复。

The matching complex of a graph consists of the sets of edges no two of which share an endpoint; again, this family of sets satisfies the no-Δ condition. It may be viewed as the clique complex of the complement graph of the line graph of the given graph. When the matching complex is referred to without any particular graph as context, it means the matching complex of a complete graph. The matching complex of a complete bipartite graph Km,n is known as a chessboard complex. It is the clique graph of the complement graph of a rook's graph,[5] and each of its simplices represents a placement of rooks on an m × n chess board such that no two of the rooks attack each other. When m = n ± 1, the chessboard complex forms a pseudo-manifold.

The matching complex of a graph consists of the sets of edges no two of which share an endpoint; again, this family of sets satisfies the no-Δ condition. It may be viewed as the clique complex of the complement graph of the line graph of the given graph. When the matching complex is referred to without any particular graph as context, it means the matching complex of a complete graph. The matching complex of a complete bipartite graph Km,n is known as a chessboard complex. It is the clique graph of the complement graph of a rook's graph,. and each of its simplices represents a placement of rooks on an m × n chess board such that no two of the rooks attack each other. When m = n ± 1, the chessboard complex forms a pseudo-manifold.

一个图的匹配复合体由不共享端点的边集合组成; 同样，这个集合家族满足 no-Δ 条件。它可以被看作是给定图的线图补图的小团复合体。当没有任何特定的图作为上下文来引用匹配复数时，它意味着一个完整图的匹配复数。完全二分图 k，n 的匹配复合被称为棋盘复合。这是一个补图图的小团图。它的每个单纯形表示在 m × n 棋盘上一个车子的位置，这样两个车子就不会互相攻击。当 m = n ± 1时，棋盘复形形成伪流形。

The Vietoris–Rips complex of a set of points in a metric space is a special case of a clique complex, formed from the unit disk graph of the points; however, every clique complex X(G) may be interpreted as the Vietoris–Rips complex of the shortest path metric on the underlying graph G.

The Vietoris–Rips complex of a set of points in a metric space is a special case of a clique complex, formed from the unit disk graph of the points; however, every clique complex X(G) may be interpreted as the Vietoris–Rips complex of the shortest path metric on the underlying graph G.

度量空间中一组点的维多里斯-里普斯复合体是由点的单位圆图形成的团复合体的一个特例，然而，每个团复合体 X (G)可以解释为底图 G 上最短路径度量的维多里斯-里普斯复合体。

脚本错误：没有“Footnotes”这个模块。 describe an application of conformal hypergraphs in the logics of relational structures. In that context, the Gaifman graph of a relational structure is the same as the underlying graph of the hypergraph representing the structure, and a structure is guarded if it corresponds to a conformal hypergraph. 

describe an application of conformal hypergraphs in the logics of relational structures. In that context, the Gaifman graph of a relational structure is the same as the underlying graph of the hypergraph representing the structure, and a structure is guarded if it corresponds to a conformal hypergraph.

描述了共形超图在关系结构逻辑中的应用。在这种情况下，关系结构的 Gaifman 图与表示该结构的超图的底层图相同，并且如果一个结构对应于一个共形超图，则该结构被保护。

Gromov showed that a cubical complex (that is, a family of hypercubes intersecting face-to-face) forms a CAT(0) space if and only if the complex is simply connected and the link of every vertex forms a flag complex. A cubical complex meeting these conditions is sometimes called a cubing or a space with walls.[1][6]

Gromov showed that a cubical complex (that is, a family of hypercubes intersecting face-to-face) forms a CAT(0) space if and only if the complex is simply connected and the link of every vertex forms a flag complex. A cubical complex meeting these conditions is sometimes called a cubing or a space with walls..

Gromov 证明了一个立方体复合体(也就是面对面交叉的一族超立方体)形成 CAT (0)空间的充要条件是，并且只有当这个复合体是简单连接的，并且每个顶点之间的连接形成一个标志复合体。满足这些条件的立方体复合体有时被称为立方体或有墙的空间。

Homology groups

Meshulam[7] proves the following theorem on the homology of the clique complex. Given integers [math]\displaystyle{ l\geq 1, t\geq 0 }[/math], suppose a graph G satisfies a property called [math]\displaystyle{ P(l,t) }[/math], which means that:

Meshulam proves the following theorem on the homology of the clique complex. Given integers l\geq 1, t\geq 0, suppose a graph G satisfies a property called P(l,t), which means that:

同调群 = = Meshulam 证明了以下关于团体复合体同调的定理。给定整数 l geq 1，t geq 0，假设图 G 满足一个称为 P (l，t)的性质，这意味着:

  • Every set of [math]\displaystyle{ l }[/math] vertices in G has a common neighbor;
  • There exists a set A of vertices, that contains a common neighbor to every set of [math]\displaystyle{ l }[/math] vertices, and in addition, the induced graph G[A] does not contain, as an induced subgraph, a copy of the 1-skeleton of the t-dimensional octahedral sphere.
  • Every set of l vertices in G has a common neighbor;
  • There exists a set A of vertices, that contains a common neighbor to every set of l vertices, and in addition, the induced graph G[A] does not contain, as an induced subgraph, a copy of the 1-skeleton of the t-dimensional octahedral sphere.


  • G 中的每一组 l 顶点都有一个公共邻居;
  • 存在一组 A 顶点，它包含每一组 l 顶点的公共邻居，此外，归纳图 G [ A ]不包含作为归纳子图的 t 维八面体球的1-骨架的副本。

Then the j-th reduced homology of the clique complex X(G) is trivial for any j between 0 and [math]\displaystyle{ \max(l-t, \lfloor {l}/{2}\rfloor)-1 }[/math].

Then the j-th reduced homology of the clique complex X(G) is trivial for any j between 0 and \max(l-t, \lfloor {l}/{2}\rfloor)-1.

然后对于0到 max (l-t，lfloor { l }/{2} rfloor)-1之间的任意 j，团复合体 X (G)的 j 次约化同调是平凡的。

See also

  • Simplex graph, a kind of graph having one node for every clique of the underlying graph
  • Partition matroid, a kind of matroid whose matroid intersections may form clique complexes

= 参见也 =

  • 单纯形图，一种对底层图的每个小团有一个节点的图
  • 分割拟阵，一种拟阵的交点可以形成小团复合体的拟阵

Notes

  1. ↑ 1.0 1.1 脚本错误：没有“Footnotes”这个模块。.
  2. ↑ 脚本错误：没有“Footnotes”这个模块。; 脚本错误：没有“Footnotes”这个模块。; 脚本错误：没有“Footnotes”这个模块。.
  3. ↑ 3.0 3.1 3.2 脚本错误：没有“Footnotes”这个模块。.
  4. ↑ 脚本错误：没有“Footnotes”这个模块。; 脚本错误：没有“Footnotes”这个模块。.
  5. ↑ 脚本错误：没有“Footnotes”这个模块。.
  6. ↑ 脚本错误：没有“Footnotes”这个模块。.
  7. ↑ Meshulam, Roy (2001-01-01). "The Clique Complex and Hypergraph Matching". Combinatorica (in English). 21 (1): 89–94. doi:10.1007/s004930170006. ISSN 1439-6912. S2CID 207006642.

References

  • .
  • .
  • .
  • .
  • .
  • .
  • .
  • .
  • .

References

  • .
  • .
  • .
  • .
  • .
  • .
  • .
  • .
  • .

Category:Algebraic topology Category:Simplicial sets Category:Hypergraphs

类别: 代数拓扑类别: 简单集类别: 超图


This page was moved from wikipedia:en:Clique complex. Its edit history can be viewed at 团复形/edithistory

取自“https://wiki.swarma.org/index.php?title=团复形&oldid=32666”