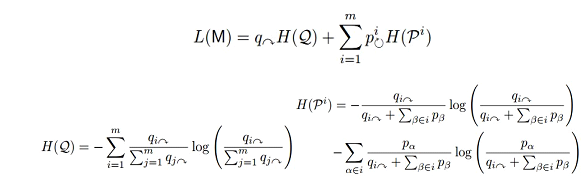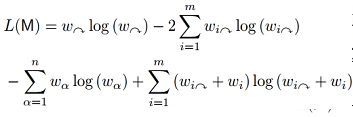网络社区划分算法
简介
使用许多互联网数据,我们都可以构建出这样的网络,其节点为某一种信息资源,如图片,视频,帖子,新闻等,连边为用户在资源之间的流动。对于这样的网络,使用社区划分算法可以揭示信息资源之间的相关性,这种相关性的发现利用了用户对信息资源的处理信息,因此比起单纯使用资源本身携带的信息来聚类(例如,使用新闻包含的关键词对新闻资源进行聚类),是一种更深刻的知识发现。
构建一个点击流网络
假设我们手头有一批用户在一段期间内访问某类资源的数据。为了减少数据数理规模,我们一般只考虑最经常被访问的一批资源。因此在数据处理中,我们考虑UV(user visit)排名前V的资源,得到节点集合|V|,然后对于一个用户i在一段时间内(例如一天)内访问的资源,选择属于|V|的子集vi。如果我们有用户访问资源的时间,就可以按照时间上的先后顺序,从vi中产生vi-1条有向边。如果我们没有时间的数据,可以vi两两间建立联系,形成vi(vi-1)/2条无向边。因为后者对数据的要求比较低,下文中,暂时先考虑后者的情况。
对于一天内的n个用户做这个操作,最后将得到的总数为 的连边里相同的边合并,得到|M|个不同的边,每条边上都带有权重信息。这样,我们就得到了V个节点,M条边的一个加权无向网络,反应的是在一天之内用户在主要的信息资源间的流动情况。在这个网络上,我们可以通过社区划分的算法对信息资源进行分类。
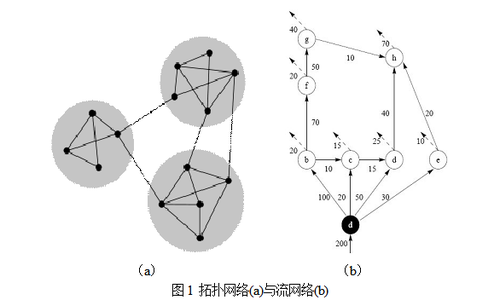
网络社区划分的两种主要思路:拓扑分析和流分析
社区划分的算法比较多,但我个人认为大致可以分为两大类:拓扑分析和流分析。前者一般适用于无向无权网络,思路是社区内部的连边密度要高于社区间。后者适用于有向有权网络,思路是发现在网络的某种流动(物质、能量、信息)中形成的社区结构。这两种分析各有特点,具体应用取决于网络数据本身描述的对象和研究者想要获得的信息。
我们可以将已知的一些算法归入这两类:
| 算法 | 优化目标 | 计算复杂度 | 适用情况 | 局限 |
|---|---|---|---|---|
| 拓扑分析 | ||||
| Q Modularity | 最大化Q-modularity | V|^2 | 无向无权多分量 | 不适用小网络 |
| Edge-Betweenness | 最小化社区间连边的betweenness | V|*|E|^2 | 有向有权多分量 | 慢 |
| Leading Eigenvector | 对拉普拉斯矩阵第二小特征根对应的特征向量聚类 | V|^2+ |E| | 无向无权多分量 | |
| Fast Greedy | 使用社区合并算法来快速搜索最大Q-modularity | E|*log(|V|) | 无向有权多分量 | 不适用小网络 |
| Multi Level | 使用社区展开算法来快速搜索最大Q-modularity | V| | 无向有权多分量 | 不适用小网络 |
| 流分析 | ||||
| Walk Trap | 最大化社区间的流距离 | E|*|V|^2 | 无向有权单分量 | |
| Label Propagation | 每个节点取邻居中最流行的标签,迭代式收敛 | V| + |E| | 无向有权单分量 | 结果不稳定 |
| Info map | 最小化随机流的编码长度 | V|*(|V|+|E|) | 有向有权单分量 | |
| Role-based community | 划分出在流中地位类似的节点 | V|^3 | 有向有权单分量 | 结果不稳定 |
上表中的分量 component指在网络中的独立“团块”。有向网络里,分量有强弱之分,强分量(strong component )中任意一个节点都可到达另外一个节点,弱分量 weak component中如果忽略连边方向,则构成强分量。无向网里分量没有强弱之分。在网络中识别强分量的算法有Kosaraju算法,Tarjan算法及其变形Gabow算法等。在这里不展开叙述。 接下来,我们逐一讨论拓扑分析和流分析中的各种算法的具体思路。
拓扑分析
计算网络的模块化程度 Q-Modularity
Q-Modularity是一个定义在[-0.5,1)区间内的指标,其算法是对于某一种社区结构,考虑每个社区内连边数与期待值之差。实际连边越是高于随机期望,说明节点越有集中在某些社区内的趋势,即网络的模块化结构越明显。Newman在2004年提出这个概念最初是为了对他自己设计的社区划算法进行评估,但因为这个指标科学合理,而且弥补了这个方面的空白,迅速成为一般性的社区划分算法的通用标准。 Q的具体计算公式如下:
- [math]\displaystyle{ Q=\sum_{ij}{\left [ {\frac{A_{ij}}{2m}-\frac{k_{i}*k_{j}}{(2m)(2m)}}\right ]}\delta (c_{i},c_{j})=\sum_{i=1}^{c}(e_{ii}-a_{i}^{2}) }[/math]
- [math]\displaystyle{ e_{ii} = \sum_{j}{\frac{A_{ij}}{2m}\delta (c_{i},c{j})} }[/math]
- [math]\displaystyle{ a_{i}=\frac{k_{i}}{2m}=\sum_{j}{a_{ij}} }[/math]
其中[math]\displaystyle{ A }[/math]是网络G对应的邻接矩阵,如果从[math]\displaystyle{ i }[/math]到[math]\displaystyle{ j }[/math]存在边,则[math]\displaystyle{ A_{ij}=1 }[/math],否则为0。[math]\displaystyle{ m }[/math]是总连接数,[math]\displaystyle{ 2m }[/math]是总度数,[math]\displaystyle{ \frac{A_{ij}}{2m} }[/math]是两节点之间连接的实际概率。[math]\displaystyle{ k_{i} }[/math]和[math]\displaystyle{ k_{j} }[/math]分别是[math]\displaystyle{ i }[/math]和[math]\displaystyle{ j }[/math]的度数。如果我们保持一个网络的度分布但对其连边进行随机洗牌,任意一对节点在洗牌后存在连接的概率为[math]\displaystyle{ \frac{k_{i}*k_{j}}{(2m)(2m)} }[/math]。上式中中括号表达的就是节点之间的实际连边概率高于期待值的程度。后面跟着一个二元函数,如果节点ij属于同一个社区,则为1,否则为0,这就保证了我们只考虑社区内部的连边。刚才这个定义是以节点为分析单位。实际上,如果以社区为分析单位看Q指标,可以进一步将其化简为[math]\displaystyle{ e_{ii} }[/math]和[math]\displaystyle{ a_{i} }[/math]之间的差。其中[math]\displaystyle{ e_{ii} }[/math]是在第[math]\displaystyle{ i }[/math]个社区内部的link占网络总link的比例,[math]\displaystyle{ a_{i} }[/math]是第[math]\displaystyle{ i }[/math]个社区和所有其他社区的社区间link数。
上式已经清楚定义了[math]\displaystyle{ Q }[/math],但在实际计算里,上式要求对社区及其内部节点进行遍历,这个计算复杂度是很大的。Newman(2006)对上式进行了化简,得到矩阵表达如下:
我们定义[math]\displaystyle{ S_{ir} }[/math]为[math]\displaystyle{ n*r }[/math]的矩阵,[math]\displaystyle{ n }[/math]是节点数,[math]\displaystyle{ r }[/math]是社区数。如果节点[math]\displaystyle{ i }[/math]属于社区[math]\displaystyle{ r }[/math],则为1,否则为0。则有
- [math]\displaystyle{ \delta (c_{i},c_{j})=\sum {S_{ir}S_{jr}} }[/math]
于是有
- [math]\displaystyle{ Q=\frac{1}{2m}\sum_{ij}\sum_{r}{\left [ {A_{ij}-\frac{k_{i}*k_{j}}{2m}}\right ]}{S_{ir}S_{jr}}=\frac{1}{2m}T_{r}(S^TBS) }[/math]
其中[math]\displaystyle{ B }[/math]是modularity matrix,其元素为
- [math]\displaystyle{ B_{ij}={A_{ij}-\frac{k_{i}*k_{j}}{2m}} }[/math]
该矩阵的行列和都是0,因为实际网络和随机洗牌后的网络度分布是不变的。特别地,在仅仅有两个社区的情况下([math]\displaystyle{ r=2 }[/math]),可以[math]\displaystyle{ S }[/math]定义为一个[math]\displaystyle{ n }[/math]长的向量,节点属于一个社区为1,属于另一个社区为-1,Q可以写成一个更简单的形式:
- [math]\displaystyle{ Q = \frac{1}{2m}\sum_{ij}{B_{ij}S_{i}S{j}}=\frac{1}{2m}S^{T}BS }[/math]
通过对社区的划分可能空间进行搜索,可以得到最大化[math]\displaystyle{ Q }[/math]值的社区划分。在这个过程会涉及数值优化的部分,例如表一中的fast greedy和multilevel就是用不同方法进行快速搜索的例子。以fast greedy为例Newman(2006),它通过不断合并社区来观察Q的增加趋势,得到了一个在最差的情况下复杂度约为O( |E|*log(|V|) ),在最好的情况下接近线性复杂度的算法。
计算网络的连边紧密度 Edge betweenness
这个思路出现得比较早(Newman, 2001)。Freeman (1975) 提出过一个叫betweenness的指标,它衡量的是网络里一个节点占据其他n-1节点间捷径的程度。具体而言,首先对每一对节点寻找最短路径,得到一个[math]\displaystyle{ n * (n-1)/2 }[/math]的最短路径集合S,然后看这个集合中有多少最短路径需要通过某个具体的节点。Newman借鉴了这个标准,但不是用来分析节点而是分析连边。一个连边的edge betweenness就是S集合里的最短路径包含该连边的个数。
定义了连边的betweenness后,就可以通过迭代算法来进行社区划分了。具体做法是先计算所有连边的betweenness,然后去除最高值连边,再重新计算,再去除最高值连边,如此反复,直到网络中的所有连边都被移除。在这个过程中网络就逐渐被切成一个个越来越小的component。在这个过程中,我们同样可以用Q-modularity来衡量社区划分的结果。这种算法定义比较清晰,也不涉及矩阵数学等运算,但问题是计算复杂度比较大。
计算网络拉普拉斯矩阵的特征向量 Leading eigenvector
一个有n个节点的网络G可以被表达为一个[math]\displaystyle{ n\times n }[/math]的邻接矩阵[math]\displaystyle{ A }[/math]。在这个矩阵上,如果节点i和j之间存在连边,则[math]\displaystyle{ A_{ij}=1 }[/math],否则为0。当网络是无向的时候,[math]\displaystyle{ A_{ij}=A_{ji} }[/math]。另外我们可以构造[math]\displaystyle{ n\times n }[/math]的度矩阵(degree matrix)[math]\displaystyle{ D }[/math]。[math]\displaystyle{ D }[/math]对角线上的元素即节点度数,例如[math]\displaystyle{ D_{ii} }[/math]为节点i的度数,所有非对角线的元素都是0。无向网的分析不存在度数的选择问题,有向网则要根据分析目标考虑使用出度还是入度。将度数矩阵减去邻接矩阵即得到拉普拉斯矩阵,即[math]\displaystyle{ L=D-A }[/math]。
L的特征根[math]\displaystyle{ \lambda_0 \lt = \lambda_1 \lt = ...\lt = \lambda_{n-1} }[/math]存在一些有趣性质。首先,最小的特征根总等于0。因为如果将[math]\displaystyle{ L }[/math]乘以一个有n个元素的单位向量,相当于计算每一行的和,刚好是节点的度的自我抵消,结果等于0。其次,特征根中0 的个数即无向网G中分量的个数。这意味着如果除了最小特征根,没有别的特征根为0,则整个网络构成一个整体。
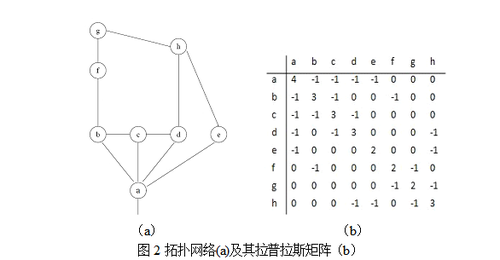
在这些特征根里,第二小的特征根(或者最小的非零特征根)[math]\displaystyle{ \lambda_1 }[/math]又叫做代数连通性 algebraic connectivity,其对应的特征向量叫做费德勒向量 Fidler vector。当[math]\displaystyle{ \lambda_1 \gt 0 }[/math],说明网络是一个整体。[math]\displaystyle{ \lambda_1 }[/math]越大,说明网络彼此间的链接越紧密。从这个定义来看,非常像前面讨论的Q-Modularity,实际上在Newman2006的文章里,确实讨论了二者在数学上的对应关系。例如对示例网络所对应的进行分析,可以得到拉普拉斯矩阵如下:
这个矩阵的特征根如下:{5.5, 4.5, 4.0, 3.4, 2.2, 1.3, 1.0, 0}。取[math]\displaystyle{ \lambda_1 =1 }[/math]时, Fidler vector={0.29, 0.00, 0.29, 0.29, 0.29, -0.58, -0.58, 0.00}。因为Fidler vector的值分别对应着图里的节点,于是可以写成{a:0.29, b: 0.00, c:0.29, d:0.29, e:0.29, f:-0.58, g:-0.58, h:0.00}。仅仅从元素的正负号就可以看出,该分析建议我们把f和g节点与其他节点分开,更细致的,对元素值大小的考察则建议把矩阵分成三个社区,{{a, c, d, e}, {b, h}, {e, f}}。回到图中考察,我们发现这个社区分类基本是合理的。
通过fast greedy方法搜索网络模块化程度Q-Modularity的最大值
因为以上两种方法都是基于Q-modularity的,只不过是搜索策略的不同,所以在此不展开讨论。
流分析
随机游走算法Walk Trap
P. Pons 和 M. Latapy 2005年提出了一个基于随机游走的网络社区划分算法。他们提出可以使用两点到第三点的流距离之差来衡量两点之间的相似性,从而为划分社区服务。其具体过程如下:首先对网络G所对应的邻接矩阵A按行归一化,得到概率转移矩阵(transition matrix)P。使用矩阵计算表达这个归一化过程,可以写作
- [math]\displaystyle{ P = D^{-1}A }[/math]
其中A是邻接矩阵,D是度矩阵。利用P矩阵的马可夫性质可知,它的t次方的元素Pijt就代表着随机游走的粒子经过t步从节点i到j的概率。其次,定义两点ij间的距离如下:
- [math]\displaystyle{ r_{ij}=\sqrt{\sum_{k=1}^{n}\frac{(P_{ik}^{t}-P_{jk}^t)^2}{d(k)}}= \left \| D^{-\frac{1}{2}}P_{i\cdot }^t - D^{-\frac{1}{2}}P_{j\cdot }^t \right \| }[/math]
其中t是流的步长。步长必须恰当选择,因为如果[math]\displaystyle{ t }[/math]太小,不足以体现网络的结构特征,如果[math]\displaystyle{ t }[/math]太大,则[math]\displaystyle{ P_{ij}^t }[/math]趋近于与[math]\displaystyle{ j }[/math]的度数[math]\displaystyle{ d(j) }[/math]成正比, 随机游出发点[math]\displaystyle{ i }[/math]的拓扑信息被抹去。作者建议的[math]\displaystyle{ t }[/math]经验值为3到5之间。[math]\displaystyle{ k }[/math]是某一个目标节点。所以这个公式描述的是经过[math]\displaystyle{ t }[/math]步,[math]\displaystyle{ ij }[/math]到目标节点[math]\displaystyle{ k }[/math]的平均流转移概率(因为这个概率与中间节点[math]\displaystyle{ k }[/math]的度数[math]\displaystyle{ d(k) }[/math]成正比,所以要除以[math]\displaystyle{ d(k) }[/math]来去除这个影响)。[math]\displaystyle{ ij }[/math]到网络所有其他点之间的距离差别越小,说明[math]\displaystyle{ ij }[/math]很可能位于及其类似的位置上,彼此之间的距离也越接近。值得注意的是,这个思路如果只考虑一个或少数的目标节点,是不合适的。因为[math]\displaystyle{ r_{ij} }[/math]实际上只是结构对称性。有可能[math]\displaystyle{ ij }[/math]在网络的两端,距离很远,但到中间某个节点的距离是相等的。但因为公式要求k要遍历网络中除了[math]\displaystyle{ ij }[/math]以外的所有节点,这个时候[math]\displaystyle{ ij }[/math]如果到所有其他节点的流距离都差不多,比较可能是[math]\displaystyle{ ij }[/math]本身就是邻居,而不仅仅是结构上的对称。如公式所示,[math]\displaystyle{ r_{ij} }[/math]表达可以写成矩阵表达,其中[math]\displaystyle{ P_{i\cdot }^t }[/math]是第[math]\displaystyle{ P }[/math]的[math]\displaystyle{ t }[/math]次方后第[math]\displaystyle{ i }[/math]行。
定义了任意两点之间的距离[math]\displaystyle{ r_{ij} }[/math]后,就可以将其推广,得到社区之间的距离[math]\displaystyle{ r_{C_1C_2} }[/math]了:
- [math]\displaystyle{ r_{C_1C_2}=\left \| D^{-\frac{1}{2}}P_{C_1\cdot }^t - D^{-\frac{1}{2}}P_{C_2\cdot }^t \right \|=\sqrt{\sum_{k=1}^{n}\frac{({P_{C_1k}^t-P_{C_2k}^t})^2}{d(k)}} }[/math]
容易看出,这个距离与节点之间的距离很相似,只不过这次是计算两个社区分别到目标节点k的流距离,而计算单个社区C到节点k的流距离时,又是对社区C内所有节点到k流距离取平均。
一旦从流结构中提取了节点相似性,社区划分就是一个比较简单的聚类问题。例如可以采取合并式聚类法如下:先将每个节点视为一个社区,然后计算所有存在连边的社区之间的流距离。然后,取两个彼此连接且流距离最短社区进行合并,重新计算社区之间的距离,如此不断迭代,直到所有的节点都被放入同一个社区。这个过程社区的数目不断减小,导致出现一个树图分层(dendrogram)结构。在这个过程中,可以使用Q-modularity的变化来指导搜索的方向。
标签扩散算法label propagation
这种算法的思路源于冯诺依曼在50年代提出的元胞自动机模型(cellular automata)和Bak等人在2002年左右做的沙堆模型。该算法的基本原理如下:首先,给全网每个节点分配一个不重复的标签(label);其次,在迭代的每一步,让一个节点采用在它所有的邻居节点中最流行的标签(如果最佳候选标签超过一个,则在其中随机抽一个),;最后,在迭代收敛时,采用同一种标签的节点被归入同一个社区。 这个算法的核心是通过标签的扩散来模拟某种流在网络上的扩散。其优势是算法简单,特别适用于分析被流所塑造的网络。在大多数情况下可以快速收敛。其缺陷是,迭代的结果有可能不稳定,尤其在不考虑连边的权重时,如果社区结构不明显,或者网络比较小时,有可能所有的节点都被归入同一个社区。
流编码算法 the Map Equation
Rosvall和Axelsson 2009年提出了一种很有意思的方法来研究网络中的流动。其核心思想是,好的社区划分要令网络上流的平均描述长度最短。他们认为,分析有向加权网络的一个好的视角是观察某类实体(货币、能量、信息)在网络上的流动。即使没有实体流动的数据,我们也可以根据网络的基本结构来推测随机游走的粒子的轨迹,然后对得到的“平均流”进行信息编码。对“平均流”的描述长度最短的编码机制,就对应着对社区的一种最有效划分。
首先要讨论的是节点层编码。最简单的方式是给每个节点分配一个独特的二进制签名。但这种编码方式并不高效,因为节点被访问的概率并不一样。为了改进,我们可以引入一个Huffman编码表(code book),在这个编码表上,每个节点都对应一个独立的二进制编码,但码长与节点被访问的概率(通过转移矩阵P在无穷步后的收敛结果来计算)相反。这样,“平均流”的信息长度就大大被降低了。
其次,我们还可以通过引入两层编码,节点编码和社区编码,来进一步降低信息长度。有了社区编码的好处是,两个或多个社区内部的节点编码是可以重复的,这就进一步降低了信息长度。需要注意的是,两层编码并不意味着像国际电话区号那样,在每个节点前加一个社区前缀码,因为这样的话其实就和单层编码没有什么区别了。这里的两层编码实际上是在利用流的“局域性”。只需要我们标识出社区的入口(即社区编码)和出口(定义在社区间连边上的编码),在此区域内访问的节点,可以直接使用节点层的编码,不用考虑社区编码。例如:11-0000-11-01-101-100-101-01-0001-0-110-011-00-110-00-111-… 在这个流中,加粗的0前面,节点都在一个社区里游走,所以直接使用节点编码,0001是一个社区出口连边(exit)编码,使用了这个编码意味着节点要跳转社区,接下来0这个社区编码被使用,意味着流进入0社区,在这里面再次直接使用节点编码,直到跳出0社区(0社区的exit被使用)。
在这个两层编码体系中,包括三类码表(code book)。第一个是主码表(master code book),决定每个社区的编码;第二个是传送门码表(exit code book),决定每个社区的出口连边的编码;第三个是节点码表(node code book),决定每个社区内的节点的编码。一旦对网络的社区划分P(partition)给定,就存在一个社区码表,一个传送门码表,和m个节点码表,其中m是社区的个数。最后,社区划分的目标就是要最小化所有码表的总长,或者按论文中的说法,平均随机游走中的一步所耗费的信息成本。
这个思路以一种很有趣的方式利用了网络社区的定义。网络社区的存在,意味着社区内的流动较多,跨越社区的流动较少。因此,一个好的社区划分意味着主码表和传送门码表被调用的次数都很少,描述的信息配额(quota)主要用于描述社区内的流动。相反,如果待分析的是一个随机的网络,或者研究者构造了一种低效的社区划分,那么主码表和传送门码表被调用的次数将会很多。特别是传送门码表,也就是错误的社区划分会大大加大这个码长。
一个总结了以上思想的公式可以表达如下,作者称之为the map equation。
其中M即对网络的某种社区划分得到m个社区。L是该划分所对应的信息描述长度。qi->代表进出第i个社区的概率(先考虑无向网络),因此q->代表社区间跳转的总概率。H(Q)是社区间跳转行为的香农信息量。Pi->代表第i个社区内节点间跳转的总概率,H(Pi)是第i个社区内节点间跳转行为的香农信息量。在公式的两个部分,信息量都用其被使用的频率进行加权。经过展开化简,可以得到简化形式如下:
最后,使用某种社区划分的搜索策略(主要有细分与合并两种)来寻找该描述长度的最小值即可。值得注意的是,在实际计算中,节点层的信息量(第三项)是不需要考虑的。
流层级算法 Role-based Similarity
Cooper和Barahona 在2010年提出了一个算法,可以揭示网络中流的层级关系。他们认为,通过对网络的邻接矩阵A进行分析,可以得到一个节点从一步到k步的出流或入流的画像(flow profile),在任意两个节点之间比较这种流画像,就可以得到节点之间的相似性,从而为社区划分服务。
具体过程如下:先得到网络的邻接矩阵A,这个时候V=AKI中的元素Vi就代表第i个节点在k步的所有出流之和。类似地,U=(AT)KI中的元素Ui就代表第i个节点在k步的入流之和。
- [math]\displaystyle{ X=\begin{bmatrix} x_1\\ \vdots \\ x_N \end{bmatrix}\equiv\underset{k_{max}}{ \underbrace{[\cdots (\beta A^T)^k1\cdots}}|\underset{k_{max}}{ \underbrace{\cdots (\beta A)^k1\cdots]}} }[/math]
如公式所示,我们可以构造n * k的矩阵Xin,其元素Xinij代表第i个节点在第k步的入流;也可以构造Xout,其元素Xoutij代表第i个节点在第k步的出流。把Xin和Xout横着拼在一起,就是X。其维度为n * 2k。在X矩阵上,第i行正好描述了节点i在k步内的所有入流和出流的信息。因此,可以通过计算第i行和j行的Cosine距离或者Manhattan距离等来定义节点相关性rij,最后得到的相关性矩阵,就可以用于聚类。
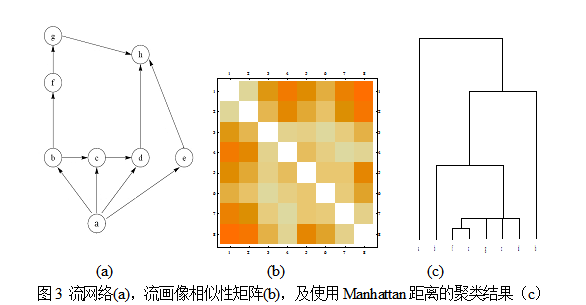
图3展示了将role-based similarity方法用于分析一个示例流网络的结果。发现分类的结果确实反映了流的层级关系。值得注意的是,虽然在论文中作者建议使用Cosine距离,但我发现在这个实例网络上,使用Manhattan距离的结果能更清晰地揭示流层级结构。因此,具体的分析要看数据的情况,这也是应用这种算法需要考虑的局限之一。
总结
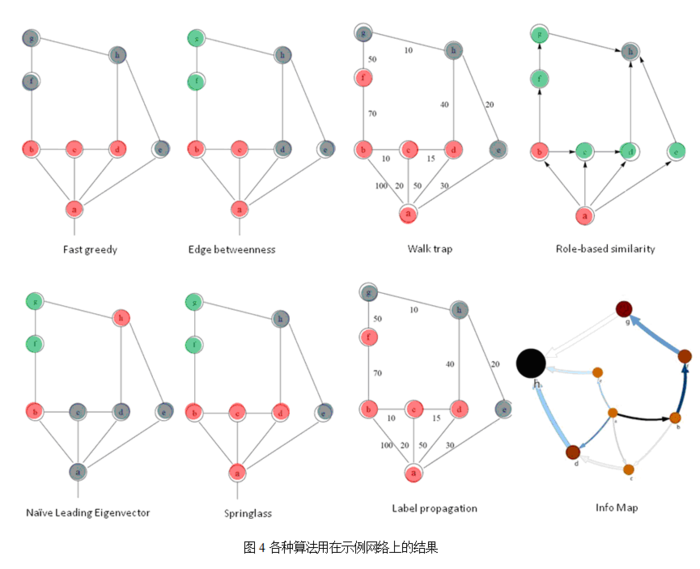
本文中我们总结了构建点击流网络之后,使用社区划分算法来对点进行聚类的不同思路。主要可以分为拓扑分析和流分析两种,从数学角度看,前者以频谱分析(Spectral analysis)为主要手段,后者以马可夫链(Markov chain)为主要建模工具。其中流编码算法较为独特,以信息论为主要工具。但值得注意的是,由于编码算法仍然是在处理流,所以本质上只是对马可夫链的一种处理。例如在图4中,编码算法没有能区分开节点,而是将所有的节点归为一个区,每个节点被访问的流概率恰好等于其Page rank值(与节点的大小和颜色深度成正比)。而我们知道Page rank也仍然是基于马可夫链的。这个时候平均每走一步要消耗2.71比特信息。
编辑推荐
集智文章
网络遇见大数据:在大型静态数据集中恢复动态网络
导语:我们正身处于大数据时代,从基础物理学到生命以及社会科学,几乎所有学科都孕育出了体量巨大的数据集,数以千计的变量纠缠其中,隐藏着许多我们未曾发现的关系与自然法则。近日发表在 Physics Reports 的综述文章,介绍了一个从大型静态数据集中恢复动态网络的统一框架,为挖掘大数据中蕴含的深层次信息提供了一种新思路。
推荐算法削弱了我们的判断力?让行为科学还你清爽信息流
导语:我们每天在网络平台上看到的信息,很大程度上是由运营平台的商业公司所编写的算法决定的。但在工具理性的背后,确实存在着网络用户对新闻平台的不满与抱怨:点开全文毫无意义的标题党、缺少“石锤”容易翻转的假新闻都在影响着网络媒介的生态。
2020年6月,一组来自柏林马克斯·普朗克人类发展研究所、布里斯托大学与哈佛大学法学院的研究者,从行为科学的角度分析了相关问题,并给出了他们的干预措施。这一研究成果发表在了 Nature Human Behaviour 上。
本中文词条由薄荷编辑,如有问题,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。