论虚拟实在的力学
作者: Email:
摘要
得益于计算机科学,特别是计算机模拟技术的发展,我们现在可以创造一个栩栩如生、活灵活现的虚拟世界,这使得人们拥有了虚实两个世界里的生活经验。我们已经进入了一个虚实混合的时代,需要新的物理学来描述这个虚实混合的宇宙。本文中,提出了一些关于基础物理学的统一及其发展方向的一些个人看法。文章包含三部分:(1)超变换。带模拟器的时空变换,它描述了处于两个不同世界中的物体间的时空变换关系;在这一部分,给出了自然的一个新图景,虚拟世界网,称作“超宇宙”;信息可以从“超宇宙”的一个世界到另一个世界。(2)相似力学。以分形几何与流体动力学的形式统一基本相互作用、相对论与量子力学的一个概念框架;在这一部分,长程相互作用被统一成平方反比作用,而短程相互作用则被看成“旋”的化合与分解。(3)人工宇宙。人工实在的物理基础;在这一部分,我们扮演造物主的角色以微观水平上的扩展的元胞自动机和宏观水平上的模拟力学的方式,创造各种各样的虚拟世界。本文的结果,作为一个物理理论,仅仅是个开端,但它大大加深了我们对自然界的认识,并提供了物理学研究的一个新视角和一套新的方法论。
谨以本文献给2005世界物理年以纪念相对论诞生100周年和爱因斯坦逝世五十周年。
引言
计算机科学的发展不仅改变了人们的生活,也改变了人们的思想。得益于计算机模拟技术的进步,我们现在可以创建一个栩栩如生、活灵活现的虚拟世界。科学家可以利用它搞研究,教师可以用它来辅助教学,而游戏玩家则可以用它来娱乐消遣。所有上面这些人都拥有虚实两个世界里的生活经验。此外,在某些艺术作品中,特别是在电影《黑客帝国》1中,我们称之为实在的这个世界被怀疑是由电脑控制的虚拟世界。我们难以辨别我们生活的这个世界是真实的还是虚拟的。总之,我们已经进入了虚实混合的时代,需要新的物理学来描述这个虚实混合的宇宙。现在,我们以下面这个问题开始我们的研究之旅:如果伟大的物理学家,阿尔伯特·爱因斯坦,生活在我们这个时代并观看了电影《黑客帝国》,那么,他会告诉我们什么呢?
图 1 爱因斯坦在观看电影《黑客帝国》。 图的左半边是真实世界而图的右半边是虚拟世界。本文中我们将给出爱因斯坦和尼奥之间的时空变换关系。
一、 超变换
模拟中的矛盾
设想一个模拟试验。我们要模拟太阳系的运行。我们可以在编程的时候设定万有引力定律的形式。比如我们可以让模拟试验中的引力常数小于我们这个世界中的引力常数,我们还可以让万有引力定律成为立方反比律,而非平方反比律。这样一来,被模拟的太阳系中的行星的速率将小于我们这个世界中的行星的速率。设想有一个物理学家生活在那个被模拟的世界里。通过长期的观察,他可以发现他那个世界里的万有引力定律,那么,它的形式必然不同于我们这个世界里的万有引力定律的形式,即,它的引力常数较小且为立方反比律。这就是说,物理定律的形式在被模拟世界与模拟世界之间不是不变的。
这样,我们就在下面这两个命题之间遇到了矛盾:“这两个世界是同样真实的”和“物理规律在这两个世界之间是不变的”。哪个对呢?
基本原理
我们坚持前者并提出如下两条基本原理:
- 所有世界同样真实;
- 被模拟事件与模拟事件共存。
前者意味着,如果一个人没有来自其他世界的启示,他就无法辨别他所存在的这个世界是真实的还是虚拟的,就像没有参照系,一个人无法辨别他是运动的还是静止的一样。第一条原理是广义相对性原理的推广,称为超广义相对性原理,它表明了真实性的相对性,即,真实性是相对的。对于一个世界而言,我们称其为真实还是虚拟依赖于我们是否生活在其中:我们称我们生活于其中的世界是真实的,而称其它世界为虚拟的。例如,如果我们生活在世界A中,我们就称它是真实的,而称另一个世界是虚拟的。但是,如果我们的意识从世界A转移进入世界B,那时,我们将称世界B是真实的而称世界A是虚拟的。因此,真实性是相对的,就像运动是相对的一样;两个世界在真实性上是平权的。一般而言,所有虚拟世界在真实性上都是平权的,没有绝对真实的世界,就像没有绝对静止的参照系一样。如果我们坚持第一条原理(同真原理),我们就不得不放弃如下命题:“物理规律在两个世界之间是不变的”。一般而言,不同世界中的物理规律的形式可以是不同的。认识到这一点,是人类认识自然过程中的一个飞跃,即:真实性不等于物理定律。
第二个原理陈述了一个事实,称作共存原理。迄今为止,主要有两类模拟器可资利用:电脑和人脑。对于电脑而言,假设在电脑模拟的世界(被模拟世界)里有一个闪烁的小球,则它在电脑所在的这个世界(模拟世界)里的对应物为电脑数字电路中的0和1(高低电平)的组合。事实上,对于被模拟世界中的任何物体,在模拟世界中都有它的对应物(即数字电路中高低电平的组合)。对于人脑而言,假设某人的幻想中有一个漂亮的女孩,则她在真实世界(即幻想者所在的这个世界)中的对应物为他大脑中进行的生物化学反应。事实上,对于一个人幻想中的任何东西,在真实世界中都有它的对应物(脑中进行的生化反应)。总而言之,被模拟事件与模拟事件共存。第二条原理说“被模拟事件与模拟事件共存”,并不意味着被模拟事件与模拟事件以相同的形式存在。以某人幻想中的女孩为例,她在被模拟世界中的存在形式是一个漂亮的女孩,然而在模拟世界中她的对应物的存在形式却是生化反应。
超变换
基于上面两条原理,我们来推导 “带模拟器的时空变换”,它也被称作“超变换”。
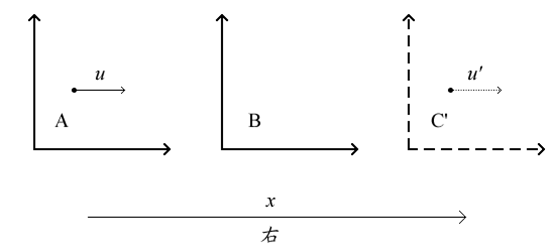
设模拟世界为R(真实世界),被模拟世界为V(虚拟世界)。设真实世界R中有一个模拟器B,它模拟着虚拟世界V。设世界R中有一个物体A,它位于模拟器B的左边,并以速度向右(向着B)运动。在世界V中有一个物体C’,它位于模拟器B的右边并以速度向右(远离B)运动。如图2所示。我们将给出物体A与C’之间的时空变换关系。
图 2 用来推导超时空变换的三个相对运动的物体。图中,B是位于真实世界R中的模拟器,它模拟着虚拟世界V。物体A在真实世界R中,并以相对于B的速度u向着B运动,而虚拟世界中的物体C’以相对于B的速度u’远离B运动。我们将推导物体A与C’之间的时空变换关系。
根据第一条原理,真实世界中的物体A与虚拟世界中的物体C’同样真实,所以,它们之间的时空变换是有意义的。
根据第二条原理,被模拟事件与模拟事件之间存在一一映射,而这一映射可被看作是模拟器上连接真实世界R和虚拟世界V的一个通道。设这一通道用字母P来表示,则P存在两个端点:一端开口于真实世界R,用PR来表示;而另一端开口于虚拟世界V,用PV来表示。PR和PV分别是模拟器B在真实世界R和虚拟世界V中的代理。因此,速度u可被定义成在真实世界中,物体A相对于PR的速度,而速度u'则可定义成在虚拟世界中,物体C’相对于PV的速度。
为了得到A与C’之间的时空变换,我们首先需要知道通过通道P的变换关系。一般地,设通过模拟器B上的通道P的时空变换关系为 [math]\displaystyle{ \hat{P}_B }[/math],而世界R中从A到B的时空变换关系为 [math]\displaystyle{ \hat{T}_{AB}^R }[/math] ,世界V中从B到C’的时空变换关系为 [math]\displaystyle{ \hat{T}_{BC}^V }[/math] ,那么,从A到C’的时空变换关系为:
[math]\displaystyle{
\hat{T}_{AC}=\hat{T}_{AB}^R\cdot\hat{P}_B\cdot\hat{T}_{BC}^V
}[/math] (1)
其中,“·”表示变换的复合。方程(1)就是带模拟器的时空变换的一般形式。
下面,我们将在某些简单的假设下考虑带模拟器的时空变换的具体形式。首先,考虑通道P两端之间的时空变换关系。设PR处的事件用[math]\displaystyle{ (x_B, y_B, z_B, t_B) }[/math]表示,PV处的事件用[math]\displaystyle{ (x_B^{\prime}, y_B^{\prime}, z_B^{\prime}, t_B^{\prime}) }[/math]表示,PV处测量的长度[math]\displaystyle{ {\Delta}x^{\prime} }[/math]在PR处测得的长度为[math]\displaystyle{ {\Delta}x }[/math]。一般说来,[math]\displaystyle{ {\Delta}x^{\prime} }[/math]和[math]\displaystyle{ {\Delta}x }[/math]之间存在空间缩放因子[math]\displaystyle{ f_s={\Delta}x^{\prime}/{\Delta}x }[/math],它表示模型与原型之间的比例关系。设通道P的长度为0,即PR和PV在“超空间”中彼此重合,则 [math]\displaystyle{ f_s={\Delta}x^{\prime}/{\Delta}x=x^{\prime}/x }[/math],于是,
[math]\displaystyle{ x_B^{\prime} = f_s\cdot{x_B} }[/math],[math]\displaystyle{ y_B^{\prime}=f_s\cdot{y_B} }[/math],[math]\displaystyle{ z_B^{\prime}=f_s\cdot{z_B} }[/math] (2)
设有一事件过程,该过程在世界V中持续的时间为[math]\displaystyle{ {\Delta}t^{\prime} }[/math],而在R中模拟该过程所用的时间为[math]\displaystyle{ {\Delta}t }[/math]。一般说来,[math]\displaystyle{ {\Delta}t^{\prime} }[/math]和[math]\displaystyle{ {\Delta}t }[/math]之间存在一个时间缩放因子[math]\displaystyle{ f_t={\Delta}t^{\prime}/{\Delta}t }[/math],它由模拟器B的运行频率决定。设穿越通道P所用的时间为0,即,对于一个事件过程而言,在R中开始模拟它的时间与它在V中开始的时间相同,则[math]\displaystyle{ f_t={\Delta}t^{\prime}/{\Delta}t=t^{\prime}/t }[/math],于是,
[math]\displaystyle{ t^{\prime}_B=f_tt_B }[/math] (3)
合并(2)和(3),我们得到穿越通道P的变换关系:
[math]\displaystyle{
\hat{P}_B=
\left\{\begin{array}{ll}
x^{\prime}_B=f_sx_B&\\
y^{\prime}_B=f_sy_B&\\
z^{\prime}_B=f_sz_B&\\
t^{\prime}_B=f_tt_B&\end{array}
\right.
}[/math] (4)
通过规定(如果我们可以的话)两个世界中的任何一个世界中的空间和时间单位,我们就可以将[math]\displaystyle{ f_s }[/math]和[math]\displaystyle{ f_t }[/math]的取值设为1,从而使[math]\displaystyle{ \hat{P}_B }[/math]成为恒等变换,
[math]\displaystyle{ \hat{P}_B=1 }[/math] (5)
于是:
[math]\displaystyle{
\hat{T}_{AC}=\hat{T}_{AB}^R\cdot\hat{T}_{BC}^V
}[/math] (6)
这就是从A到C’的时空变换关系。
宇称破缺
看个例子。如果世界R中的变换是Lorentz变换2,那么在R中必存在“光速不变原理”。设R中的光速为,则从A到[math]\displaystyle{ P_R }[/math]的变换是:
[math]\displaystyle{
\hat{T}_{AB}^R=
\left\{\begin{array}{ll}
x_B=\frac{c}{\sqrt{c^2-u^2}}(x_A+ut_A)&\\
y_B=y_A&\\
z_B=z_A&\\
t_B=\frac{c}{\sqrt{c^2-u^2}}(t_A+\frac{ux_A}{c^2})
&\end{array}
\right.
}[/math] (7)
如果V中也遵循Lorentz变换,则V中必有“光速不变原理”成立。设V中的光速为[math]\displaystyle{ c^{\prime} }[/math],则从[math]\displaystyle{ P_V }[/math]到[math]\displaystyle{ c^{\prime} }[/math]的变换是:
[math]\displaystyle{
\hat{T}_{BC}^V=
\left\{\begin{array}{ll}
x^{\prime}_C=\frac{c^{\prime}}{\sqrt{c^{\prime2}-u^{\prime2}}}(x^{\prime}_B+u^{\prime}t^{\prime}_B)&\\
y^{\prime}_C=y^{\prime}_B&\\
z^{\prime}_C=z^{\prime}_B&\\
t^{\prime}_C=\frac{c^{\prime}}{\sqrt{c^{\prime2}-u^{\prime2}}}(t^{\prime}_B+\frac{u^{\prime}x^{\prime}_B}{c^{\prime2}})
&\end{array}
\right.
}[/math] (8)
设[math]\displaystyle{ P_B }[/math]可被设为恒等变换,则:
[math]\displaystyle{
\hat{P}_B=
\left\{\begin{array}{ll}
x^{\prime}_B=x_B&\\
y^{\prime}_B=y_B&\\
z^{\prime}_B=z_B&\\
t^{\prime}_B=t_B
&\end{array}
\right.
}[/math] (9)
将[math]\displaystyle{ \hat{T}_{AB}^R }[/math]、[math]\displaystyle{ \hat{T}_{BC}^V }[/math]和[math]\displaystyle{ \hat{P}_B }[/math]代入[math]\displaystyle{ \hat{T}_{AC} }[/math],我们得到:
[math]\displaystyle{
\hat{T}_{AC}=
\left\{\begin{array}{ll}
x^{\prime}_C=\frac{cc^{\prime}}{\sqrt{(c^2-u^2)(c^{\prime2}-u^{\prime2})}}((1-\frac{uu^{\prime}}{c^2})x_A+(u-u^{\prime}t_A))&\\
y^{\prime}_C=y_A&\\
z^{\prime}_C=z_A&\\
t^{\prime}_C=\frac{cc^{\prime}}{\sqrt{(c^2-u^2)(c^{\prime2}-u^{\prime2})}}((1-\frac{uu^{\prime}}{c^{\prime2}})t_A+(\frac{u}{c^2}-\frac{u^{\prime}}{c^{\prime2}}x_A))
&\end{array}
\right.
}[/math] (10)
这就是从A到C’的时空变换关系。
以[math]\displaystyle{ x^{\prime}_C }[/math]、[math]\displaystyle{ y^{\prime}_C }[/math]、[math]\displaystyle{ z^{\prime}_C }[/math]和[math]\displaystyle{ t^{\prime}_C }[/math]为自变量,反解[math]\displaystyle{ \hat{T}_{AC} }[/math]中的方程,我们可以得到[math]\displaystyle{ \hat{T}_{AC} }[/math]的[math]\displaystyle{ \hat{T}_{CA} }[/math]逆变换。公式[math]\displaystyle{ \hat{T}_{AC} }[/math]和[math]\displaystyle{ \hat{T}_{CA} }[/math]表示的是处于两个不同世界中的物体之间的时空变换关系。
由[math]\displaystyle{ \hat{T}^R_{BA} }[/math],我们可以通过微分运算得到R中的速度变换公式由[math]\displaystyle{ \hat{V}^R_{BA} }[/math]。同样,我们也可以通过微分运算从[math]\displaystyle{ \hat{T}^R_{BC} }[/math]得到V中的速度变换公式[math]\displaystyle{ \hat{V}^R_{BC} }[/math]。
现在我们考虑A和C’之间的相对速度。设由[math]\displaystyle{ \hat{V}^R_{BA} }[/math]得到的C’相对于A的速度为[math]\displaystyle{ v_{AC} }[/math],而由[math]\displaystyle{ \hat{V}^V_{BC} }[/math]得到的A相对于C’的速度为[math]\displaystyle{ v^{\prime}_{CA} }[/math]。因为两个世界中的时空变换公式不相同,所以一般说来,速度变换的公式[math]\displaystyle{ \hat{V}^R_{BA} }[/math]和[math]\displaystyle{ \hat{V}^V_{BC} }[/math]也就不相同。因此,[math]\displaystyle{ v_{AC} }[/math]就不一定等于[math]\displaystyle{ -v^{\prime}_{CA} }[/math]。
例如,从(7)和(8)我们可以得到:
[math]\displaystyle{
v_{AC}=\frac{u^{\prime}-u}{1-\frac{uu^{\prime}}{c^2}}
}[/math] (11)
和
[math]\displaystyle{
v^{\prime}_{CA}=\frac{u-u^{\prime}}{1-\frac{u^{\prime}u}{c^{\prime2}}}
}[/math] (12)
若[math]\displaystyle{ c\ne{c^{\prime}} }[/math],则[math]\displaystyle{ v_{AC}\ne{v^{\prime}_{CA}} }[/math]。
作为一个一般命题:
[math]\displaystyle{ v=v^{\prime} }[/math] (命题1)
(对于两个相对运动的物体A和B,A相对于B的速度和B相对于A的速度必是等大反向的),对于分处在两个世界中的物体而言,不一定总是成立的。
注意到这一点后,我们不得不澄清我们所使用的符号。前面的u是A相对于B的速度,须重写为[math]\displaystyle{ u_{BA} }[/math],而[math]\displaystyle{ u^{\prime} }[/math]前面的是C’相对于B的速度,须重写为[math]\displaystyle{ u^{\prime}_{BC} }[/math]。
世界分类
事实上,即使对于同一个世界中的两个物体,我们也没有足够的理由认为(命题1)总是成立。在现存的时空变换关系中,比如在伽利略变换或洛仑兹变换中,(命题1)只是一个先验的假设。
一般地,设某世界中从A到B的时空变换关系为[math]\displaystyle{ \hat{T}_{AB} }[/math],而B相对于A的速度为[math]\displaystyle{ u_{AB} }[/math],即:
[math]\displaystyle{
\hat{T}_{AB}=(x_B,y_B,z_B,t_B)=f(x_A,y_A,z_A,t_A,u_{AB})
}[/math] (13)
存在两条得到[math]\displaystyle{ \hat{T}_{BA} }[/math]的途径:其一是通过反解[math]\displaystyle{ \hat{T}_{AB} }[/math]中的方程,结果用[math]\displaystyle{ \hat{T}^r_{BA} }[/math]来表示,即:
[math]\displaystyle{
\hat{T}^r_{BA}=(x_A,y_A,z_A,t_A)=f^{-1}(x_B,y_B,z_B,t_B,u_{AB})
}[/math] (14)
另一条途径是通过交换[math]\displaystyle{ \hat{T}_{AB} }[/math]中的事件符号,并用[math]\displaystyle{ u_{BA} }[/math]代替[math]\displaystyle{ u_{AB} }[/math],结果用[math]\displaystyle{ \hat{T}^s_{BA} }[/math]来表示,即:
[math]\displaystyle{
\hat{T}^s_{BA}=(x_A,y_A,z_A,t_A)=f(x_B,y_B,z_B,t_B,u_{BA})
}[/math] (15)
哪个对呢?前者是直接的数学运算,是正确的,而后者是否成立依赖于我们能否从[math]\displaystyle{ u_{AB} }[/math]得到[math]\displaystyle{ u_{BA} }[/math]。在现存的时空变换关系中,比如伽利略变换或洛仑兹变换中,[math]\displaystyle{ u_{BA} }[/math]只是先验地被认为等于[math]\displaystyle{ -u_{AB} }[/math],而这对于伽利略或洛仑兹变换来说是自洽的,即,在[math]\displaystyle{ u_{BA}=-u_{AB} }[/math]的条件下,[math]\displaystyle{ \hat{T}^r_{BA}=\hat{T}^s_{BA} }[/math]。但是,如果[math]\displaystyle{ \hat{T}_{AB} }[/math]是不同于伽利略或洛仑兹变换的其它形式,那么在[math]\displaystyle{ u_{BA}=-u_{AB} }[/math]的条件下,[math]\displaystyle{ \hat{T}^r_{BA} }[/math]就不一定等于[math]\displaystyle{ \hat{T}^s_{BA} }[/math]。
根据如下命题:
[math]\displaystyle{ \hat{T}^r_{BA}=\hat{T}^s_{BA} }[/math]当[math]\displaystyle{ u_{BA}=-u_{AB} }[/math] (命题2)
是否成立,世界可以被分成两类:“变换对称世界”和“变换非对称世界”。前者满足(命题2)而后者不满足(命题2)。如果我们这个世界遵循洛仑兹变换的话,那么它就是一个“变换对称”世界。
世界风
设想有两个物体,一个处于“变换对称”世界中,另一个处于“变换非对称”世界中,现在,我们考虑它们之间的时空变换关系。例如:
[math]\displaystyle{ \hat{T}_{BA}^R= \left\{\begin{array}{ll} x_A=\frac{1}{\sqrt{1-\frac{u^2_{BA}}{c^2}}}(x_B-u_{BA}t_B)&\\ t_A=\frac{1}{\sqrt{1-\frac{u^2_{BA}}{c^2}}}(t_B-\frac{u_BA}{c^2}x_B) &\end{array} \right. }[/math] [math]\displaystyle{ \hat{T}_{BC}^V= \left\{\begin{array}{ll} x^{\prime}_C=\frac{1}{\sqrt{1-\frac{u^{\prime2}_{BA}}{c^{\prime2}}}}(x_B-u_{BC}t_B)&\\ t^{\prime}_C=\frac{1}{\sqrt{1-\frac{u^{\prime2}_{BA}}{c^{\prime2}}}}(\frac{u^{\prime}_BC}{c^{\prime2}}x_B-t_B) &\end{array} \right. }[/math] (16)
注意[math]\displaystyle{ \hat{T}_{BC}^V }[/math]中的[math]\displaystyle{ t^{\prime}_C }[/math],它的形式不同于通常的洛仑兹变换,这使得V是一个“变换非对称”世界。
由(16),我们可以得到速度变换公式:
[math]\displaystyle{ \hat{V}_{BA}^R= \left\{\begin{array}{ll} v_A=\frac{v_B-u_{BA}}{1-\frac{u_{BA}v_B}{c^2}} &\end{array} \right. }[/math] [math]\displaystyle{ \hat{V}_{BC}^V= \left\{\begin{array}{ll} v_C=\frac{v_B-u^{\prime}_{BC}}{\frac{u^{\prime}_{BC}v_B}{c^{\prime2}}-1} &\end{array} \right. }[/math] (17)
令[math]\displaystyle{ c^{\prime}=0.5c }[/math],[math]\displaystyle{ u_{BA}=0.3c }[/math],[math]\displaystyle{ u^{\prime}_{BC}=0.7c^{\prime}=0.35c }[/math],则由(17),我们得到:
[math]\displaystyle{ v_{AC}=\frac{v_B-u_{BA}}{1-\frac{u_{BA}v_B}{c^2}}=\frac{0.35c-0.3c}{1-\frac{0.35c*0.3c}{c^2}}=0.0559c }[/math]
[math]\displaystyle{ v_{CA}=\frac{v_B-u^{prime}_{BC}}{\frac{u^{prime}_{BC}*v_B}{c^{\prime2}}-1}=\frac{0.3c-0.35c}{\frac{0.3c*0.35c}{(0.5c)^2}-1}=0.0862c }[/math] (18)
在(18)中,C’相对于A的速度[math]\displaystyle{ v_{AC}=0.0559c\gt 0 }[/math],表示“从A的观点看,C’运动的比A快,A无法追上C’(在R中)”;而同时,A相对于C’的速度[math]\displaystyle{ v_{CA}=0.0862c\gt 0 }[/math],表示“从C’的观点看,A运动的比C’快,A可以追上C’(在V中)”。这里,关于“物体A和C’是否能够相遇”,A和C’看法不一。这听上去像一个悖论,然而却是事实。
再令[math]\displaystyle{ c^{\prime}=0.5c }[/math],[math]\displaystyle{ u_{BA}=0.3c }[/math],[math]\displaystyle{ u^{\prime}_{BC}=-0.7c^{\prime}=0.35c }[/math],即将前面的A相对于B的速度和C’相对于B的速度都反个方向,那么,由(17)我们得到:
[math]\displaystyle{ v_{AC}=\frac{v_B-u_{BA}}{1-\frac{u_{BA}v_B}{c^2}}=\frac{-0.35c+0.3c}{1-\frac{0.35c*0.3c}{c^2}}=-0.0559c }[/math]
[math]\displaystyle{ v_{CA}=\frac{v_B-u^{prime}_{BC}}{\frac{u^{prime}_{BC}*v_B}{c^{\prime2}}-1}=\frac{-0.3c+0.35c}{\frac{(-0.3c)*(-0.35c)}{(0.5c)^2}-1}=-0.0862c }[/math] (19)
在(19)中,C’相对于A的速度[math]\displaystyle{ v_{AC}=-0.0559c\lt 0 }[/math],意味着“从A的观点看,C’跑得比A快,C’可以追上A(在R中)”;而同时,A相对于C’的速度[math]\displaystyle{ v_{CA}=-0.0862c\lt 0 }[/math],意味着“从C’的观点看,A跑得比C’快,C’追不上A(在V中)”。这里,关于“物体A和C’能否相遇”,A和C’的看法仍不一样。
同时考虑(18)中的和(19)中的,我们将发现一个有趣的现象:如果所有速度都朝右,我们将会看到A和C’在世界V中相遇,而如果所有的速度都向左,我们将会看到C’和A在世界R中相遇,这意味着“向右,A跑得比C’快,而向左,C’跑得比A快”。
形象地说,就像一个胖子和一个瘦子在风中赛跑。如果顺风,胖子比瘦子跑得快,因为大体积可以得到更大的风的助力;如果逆风,瘦子比胖子跑得快,因为小体积可以遭受更小的风的阻力。这种由于两个世界中的时空变换关系不同而造成的类似于风的现象,称为“世界风”。
超宇宙
在上面的推导中,B是一个模拟器,C’是一个由B模拟的虚拟世界中的物体。如果C’仍是一个模拟器,它又模拟了另外一个虚拟世界V’,而在V’中,有一个物体D’’向右(远离C’)运动,那么,A和D’’之间的时空变换关系又是什么呢?下面我们将“带模拟器的时空变换”推广到递归模拟的情形。
现在,考虑一个虚拟世界链:
[math]\displaystyle{
W_1\to{W_2}\to\dots\to{W_n}
}[/math] (20)
其中,“[math]\displaystyle{ \hat{P_{S_1}} }[/math]”表示左边的世界中有一个模拟器,它模拟了右边的世界。箭头“[math]\displaystyle{ \hat{P_{S_2}} }[/math]”称为“模拟箭头”,它表示模拟关系。模拟箭头左边的世界称为“父世界”,而模拟箭头右边的世界称为“子世界”。设W1中有模拟器S1,通过它的通道变换用[math]\displaystyle{ \hat{P_{S_1}} }[/math]表示,W2有模拟器S2,通过它的通道变换用[math]\displaystyle{ \hat{P_{S_2}} }[/math]表示,等等;直至Wn-1中的模拟器Sn-1,它模拟着世界Wn,而通过它的通道变换用[math]\displaystyle{ \hat{P_{S_{n-1}}} }[/math]来表示。那么,位于世界W1中的物体A1和位于世界Wn中的物体An之间的时空变换关系就是这些虚拟世界中的各自变换的复合变换:
[math]\displaystyle{
\hat{A_{A_1A_n}}=\hat{T^{W_1}}\cdot\hat{P_{S_1}}\cdot\hat{T^{W_2}}\cdot\hat{P_{S_2}}\dots\hat{P_{S_{n-1}}}\cdot\hat{T^{W_n}}
}[/math] (21)
如果各模拟器的通道变换可以被设置成恒等变换,那么,(21)可被简化成:
[math]\displaystyle{
\hat{A_{A_1A_n}}=\hat{T^{W_1}}\cdot\hat{T^{W_2}}\dots\hat{T^{W_n}}
}[/math] (22)
这就是处于递归虚拟世界中的两个物体之间的时空变换关系。
虚拟世界链有三种逻辑状态: [math]\displaystyle{ \underbrace{\dots\to{W_{i-1}}\to{W_i}\to{W_{i+1}}\to\dots}_{(i)} }[/math],[math]\displaystyle{ \underbrace{W_1\to{W_2}\to\dots\to{W_n}\to{W_1}}_{(ii)} }[/math],[math]\displaystyle{ \underbrace{W_1\to\dots\to{W_i}\dots\to{W_n}\dots\to{W_i}}_{(iii)} }[/math] 这里我们引入一个新概念“超宇宙”。虚拟世界链的三种逻辑状态分别对应超宇宙结构的三种基本类型。第一种基本类型称为L (line)型超宇宙,它是两端开口的结构。第二种基本类型称为O(cylcle)型超宇宙,它是一个闭的结构。第三种基本类型称为P(polliwog)型超宇宙,它是一端开口一端封闭的结构。
对于第二种基本类型的超宇宙结构来说,虚拟世界链开始于W1,当到达虚拟世界Wn时,Wn中有一个模拟器Sn,它所模拟的世界恰好是W1。
根据(22)有:
[math]\displaystyle{
\hat{A_{A_1A_{n+1}}}=\hat{T^{W_1}}\cdot\hat{T^{W_2}}\dots\hat{T^{W_n}}\cdot\hat{T^{W_1}}=\hat{T^{W_1}}
}[/math] (23)
于是有:
[math]\displaystyle{
\hat{T^{W_1}}\cdot\hat{T^{W_2}}\dots\hat{T^{W_n}}=\hat{1}
}[/math] (24)
和
[math]\displaystyle{
\hat{T^{W_2}}\dots\hat{T^{W_n}}\cdot\hat{T^{W_1}}=\hat{1}
}[/math] (25)
对于第三种基本类型的超宇宙结构来说,虚拟世界链起始于W1,当到达Wn时,Wn中有一个模拟器Sn,它模拟着世界Wi,其中。
根据(22)有:
[math]\displaystyle{
\hat{T^{W_{i+1}}}\dots\hat{T^{W_n}}\cdot\hat{T^{W_i}}=\hat{1}
}[/math] (26)
和
[math]\displaystyle{
\hat{T^{W_i}}\dots\hat{T^{W_n}}=\hat{1}
}[/math] (27)
对于第二、第三种基本类型的超宇宙结构来说,由于存在(24)、(25)、(26)、(27)这些限制,各虚拟世界中的时空变换关系就不能是任意的形式,它们要满足这些限制条件。
超宇宙结构的存在,显示出了自然界的“自模拟”属性,它意味着整个超宇宙的运行可以被它的一个子宇宙的一部分所模拟。自模拟属性是“存在”的自相似性。约束条件(24)、(25)、(26)、(27)称为“自模拟约束”。在上面的推导中,如果V=R,则意味着由B所模拟的虚拟世界恰好就是B所在的那个世界,那么,和的形式相同。在此情况下,A, B和C’之间的时空变换关系就是处于同一个世界中的三个物体之间的时空变换关系。
图 3 超宇宙结构(一部分)示意图。图中每个矩形代表一个模拟器,每个椭圆代表一个虚拟世界。实线表示“包含”关系,即某世界包含某模拟器,而虚线表示“模拟”关系,即某模拟器模拟某世界。Wn-1---Sn-1…Wn---Sn…Wn+1---Sn+1…Wn+2是L型超宇宙的一个例子;Wn---Sn…Wn+1---Sn+1…Wn+2---Sn+2…Wn是O型超宇宙的一个例子;Wn-1---Sn-1…Wn---Sn…Wn+1---Sn+1…Wn+2---Sn+2…Wn+3---Sn+3…Wn是P型超宇宙的一个例子;超宇宙(Super Universe,简称superverse),也叫“模拟多宇宙” (Simulational Multiverse,简称simuverse),它的一个节点(即一个虚拟世界),被称作一个“人工宇宙”(Artificial Universe,简称artiverse)。
现在想象每个世界中有多个模拟器,我们就会得到一幅图景——它是一个虚拟世界的网络,在该网络上模拟器是“边”,虚拟世界是“节点”,而三种基本类型L、O、P的结构是叶子,如图 3 所示。信息从超宇宙的一个世界流向另一个世界,而我们的世界不过是超宇宙上的一个节点而已。模拟我们这个世界的那个模拟器,我们称之为“本模拟器”。
验证实验
我们设计了两个虚实混合的实验来检验超变换理论。一个是粒子衰变实验,另一个是粒子追赶实验。图 4 给出了这两个实验的示意图。
图片206欠缺
图 4 两个虚实混合实验的示意图。OA处的红线是发射实粒子的位置。OC处的绿线(在电脑屏幕上)是接受(或发射)虚粒子的位置。PR(红色小圈)是接受实粒子的靶标,它连着一台计算机,该计算机上正在运行着能够产生虚拟粒子的模拟程序。PR同时也是一个能够发射实粒子的装置,该装置可由计算机上运行着的模拟程序触发,当有一个向左运动的虚粒子到达PV时。PV(绿色小圈)是电脑屏幕左边线的中点,模拟程序产生的虚粒子就是从这里以一定的速度开始向右运动的。
1. 粒子衰变
这个实验是被设计来检验复合变换(公式10)的正确性的。设有一个粒子从OA(R中的红线)处发射出来,并以速度u向右运动。设它的固有寿命为[math]\displaystyle{ t_0 }[/math]。OA与OB之间的距离为d,OB与OC’(计算机屏幕上的绿线)之间的距离为[math]\displaystyle{ d^{\prime} }[/math]。当粒子到达[math]\displaystyle{ P_R }[/math]时,它轰击到靶上,同时一个模拟程序被触发,在V(计算机模拟的虚拟世界)中生成一个虚粒子,并把真实粒子剩余的寿命赋予该虚粒子。该虚粒子从[math]\displaystyle{ P_V }[/math](计算机屏幕左边线的中点)出发,以速度[math]\displaystyle{ u^{\prime}(=u) }[/math]向右运动。设V中的时空变换关系也是洛仑兹变换,不过,其中的光速为[math]\displaystyle{ c^{\prime} }[/math]。现在设是一个常数[math]\displaystyle{ d^{\prime} }[/math],问:d应为多长才能在OC’处恰好接收到(虚)粒子。我们可根据公式(10)算出该距离d,如果它与实验事实相符,就验证了超变换(复合变换)的正确性。
2. 粒子追赶实验
这个实验被设计来检验超变换的速度变换公式。设[math]\displaystyle{ c^{\prime}=0.5c }[/math]。
首先,我们观察向右的粒子追赶。设想有一个实粒子以向右的速度[math]\displaystyle{ u=0.3c }[/math],从OA发出,与此同时(以OB为参照系),另一个虚粒子以向右的速度[math]\displaystyle{ u^{\prime}=0.7c^{\prime}=0.35c }[/math]从PV发出。根据(18)式,我们将看到A与C’在电脑屏幕(代表虚拟世界V)上相遇。
其次,我们观察向左的粒子追赶。设有个虚拟粒子以向左的速度[math]\displaystyle{ u^{\prime}=-0.7c^{\prime}=-0.35c }[/math]从OC’发出,与此同时(以OB为参照系),另一个实粒子以向左的速度[math]\displaystyle{ u=0.3c }[/math]从[math]\displaystyle{ P_R }[/math]发出。根据(19)式,我们将看到C’和A在真实世界R中相遇。
如果在实验中这些现象真的被观察到了,超变换的速度变换公式的正确性就得到了验证。
实践故事
故事1 游鱼和飞鸟——发生在自然中的故事
设想天空中有只飞鸟,湖水里有条游鱼。湖面上有个游泳者(B),他的一只眼睛在水里,而另一只眼睛在空气中。通过他的左眼,他看到鱼(A)从左边向它游来,而通过他的右眼,他看到鸟(C)在他右边离他飞去。用左眼,他测得鱼相对于他的速度为,用右眼,他测得鸟相对于他的速度为。因为水中和空气中的速度变换都遵循洛仑兹变换,但是,水中的光速和空气中的光速是不相等的,因此,这个游泳者会告诉我们,飞鸟相对于游鱼的速度和游鱼相对于飞鸟的速度并非等大反向。
故事2 警察和小偷——发生在未来的故事
设想在未来,由于人机接口技术的发展,人可以进入由电脑模拟的虚拟世界。设有一个警察(A)和一个小偷(C)。警察拿着一根警棍而小偷拥有一把手枪。警察和小偷曾在现实世界R中发生搏斗。在小偷开枪之前,他的手枪在搏斗中被打坏了,但不是大毛病。任何会使用手枪的人,用十分钟的时间(固有时间)就可以修好它。设小偷拿着那把被打坏了的手枪向东跑,而警察手提警棍在他后面追。当小偷遇到前面的一个模拟器B时,他进入虚拟世界V。进入虚拟世界后,小偷开始修理他的手枪。当警察赶到模拟器B时,如果该警察足够聪明并且知道超时空变换的话,他在决定是否进入虚拟世界V继续追赶小偷之前,会先算一算。如果他赶到模拟器B所用的(R世界中的)时间加上他进入虚拟世界V后,追上小偷所用的虚拟世界中的时间的总和,超过了小偷修好手枪所用的时间,那么,警察是不敢进入虚拟世界抓小偷的,因为警棍显然不是手枪的对手。
故事3 故事2的当代版本——发生在游戏中的故事
设想我们举行一场虚实混合的比赛。有两个参赛者,他们都是游戏玩家和长跑健将。但我们让他们玩的游戏却很平常:“警察抓小偷”。游戏玩家A扮演警察而游戏玩家C扮演小偷。我们设想游戏场景如下:
操场上有两条跑道。在跑道的终点处安放一台计算机。该计算机配置了一个很大的屏幕,两个游戏玩家都能看到它。该计算机还配置了两个键盘,分别供两个游戏玩家使用。两个游戏玩家首先在两条跑道上赛跑。当他们到达跑到终点时,各用一个键盘,开始计算机游戏的角逐:大名鼎鼎的警察捉小偷的游戏(注:一个简单的计算机游戏,其中小偷在前面跑,警察在后面追,意欲抓住小偷)。
玩家A(警察)让玩家C(小偷)先跑。过一小会儿,玩家A开始起跑去追玩家C。当玩家C到达终点线时,他通过按他键盘上的“回车”键进入计算机游戏;与此同时,有个小偷(游戏中的角色)出现在大屏幕左边线的中点,并开始沿着水平线向右(即向着大屏幕右边线的中点)跑去。当玩家A到达终点线时,他也通过按他键盘上的“回车”键进入游戏;与此同时,有一个警察(游戏中的角色),出现在大屏幕左边线的中点,并开始追赶小偷。同时,启动一个模拟修手枪的程序。
在这个游戏中,模拟器是计算机,而它的通道P就是计算机的电路;通道P在真实世界中的端口PR就是键盘上的“回车”键,而通道P在虚拟世界中的端口PV就是电脑屏幕左边线的中点。虚拟世界V中的时空变换关系被定义成电脑屏幕上移动着的物体与电脑屏幕左边线中点之间的时空变换关系。
我们制定游戏规则如下:如果玩家A进入计算机游戏并且捉住了玩家C扮演的小偷,就算玩家A赢;如果警察被小偷射杀,就算玩家C赢。获胜者将赢得1000元RMB,该奖金的一半由比赛举办方(即我们)支付,另一半由失败者支付。但是,在玩家A进入计算机游戏之前,如果两个游戏玩家中的任何一个主动认输的话,则认输者无须付钱,而获胜者将得到举办方支付的500元。
在这样的游戏规则下,在玩家A进入计算机游戏之前,两个玩家都必须计算一下,来决定是否认输以减小自己的损失。在此情形下,谁懂得超时空变换,谁就可以减少损失,多赢钱。
三个世界的统一
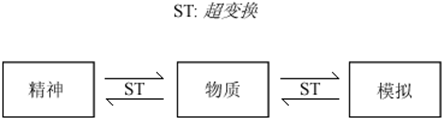
图 5 超变换桥接了3个世界:客观物质世界、主观精神世界和计算机虚拟世界。这三类世界被统一成虚拟实在。
上述文中共提到了三类模拟器:本模拟器,人脑和计算机。“本模拟器”是我们这个世界运行于其上的那个模拟器,它是一个“神”造的模拟器。人脑是我们这个世界演化的结果,而计算机是人造的模拟器。这三类模拟器模拟了三类世界:客观物质世界、主观精神世界和计算机虚拟世界。这三类世界经由“超变换”彼此联系,并被统一成虚拟实在:这使得给出自然的一个统一的描述成为可能。
讨论
1、存在的虚拟性。“同真原理”也可称为“庄子原理”。中国有一部古书名叫《庄子》3。在该书的第二篇,作者庄周讲述了一个故事:一天,他梦到自己变成了一只蝴蝶。在梦中,他完全忘记了自己是庄周,是一个人,而只知道自己是一只蝴蝶;而当他醒来的时候,他发现自己是庄周,是一个人,而不是一只蝴蝶。于是,他就对下面这个问题产生了困惑:我到底是一人而做梦变成蝴蝶呢,还是我本来是一只蝴蝶而现在做梦变成了人呢?庄子可能是第一个意识到真实性的相对性,即存在的虚拟性的人。至此,如果有人说:“我们生活在某人的梦中”,那已不再是个玩笑话了。
2、思想的真实性。现在做一个思想实验。闭上眼睛,想象有一个金属球在绕着你转动。首先想象它在顺时针转,转动数圈后,试着让它突然开始逆时针转。要完成这个变化,你会觉得吃力。即是说,你会清晰地感觉到,你想象中的金属球具有惯性,这意味着它和真实世界里的金属球一样,是有质量的。总之,你想象中的东西和你一样真实。
3、实在与物理定律。爱因斯坦认为处于不同参考系中的人们会感受到相同的“物理实在”,而我们更进一步,认为处于不同世界中的人们将感受同样的“实在”。请注意我们和爱因斯坦的区别。爱因斯坦使用“物理实在”这个词,而我们使用“实在”这个词。即是说,同样的“实在”并不意味着同样的物理规律,即“实在”不等于物理定律,这是我们的自然观的一个实质性的进步。爱因斯坦受限于他的时代,不可能意识到“实在”与物理定律之间的差异。然而今天,得益于模拟技术的发展,我们可以创造一个有着不同于我们这个世界的物理规律的世界。我们已经并且正在扮演着上帝的角色,也许只是部分地,然而这一事实却足以大大地加深我们对于自然的理解。
4、信息守恒律。在超宇宙图景中,物体从一个世界转移进入另一个世界,实际上是物体在这两个不同世界中的表示。一次转移操作对应一个再创造的过程。“物体C从世界A转移到世界B”是指在B世界中根据C所携带的A世界中的信息,利用B中的元素再造一个C。确保物体C是物体C而非其它,就要求信息的守恒。
5、意识。设想在将来,由于人机接口技术的发展,人们可以进入由计算机模拟的虚拟世界。如果意识可以从一个世界转移进入另一个世界的话,它的本质必是信息的。即是说,意识的本质是信息流,是人脑作为一个模拟器的运行过程。此外,模拟关系联接了主观世界与客观世界,使得给出关于自然的一个统一的描述成为可能。模拟器是计算器,既能够运算的机器。由此可知,任何具有运算能力的东西,可能都有某种程度的意识。即是说,意识可能是宇宙物质的一个普遍属性(泛精神说)。
6、自由意志。自由意志的本质是两个有着不同物理规律的世界之间的关联。自由意志的出现需要两个因素:差异和关联。由于差异的存在,一个世界(通常指模拟世界)中的物理规律不能决定另一个世界(通常指被模拟世界)中发生的现象,这就确保了自由意志存在的(超)空间的存在。相反,如果两个世界中的物理规律相同,它们就可以被看作一个(更大的)世界,这样便不会有自由意志存在的余地。由于关联的存在,自由意志才能表现出来。如果两个不同(指物理规律不同)的世界之间没有关联,那么,一个人只能生活在两个世界中的一个,要么是这个世界,要么是那个世界,这样一来,对他而言,就好像只存在一个世界一样,因而也无法表现出自由意志。我们之所以有自由意志,是因为我们生活在两个不同(指物理规律不同)的世界的叠加态中,即我们同时生活在现实(客观世界)与幻想(主观世界)之中。如果我们只生活在一个世界中,我们不会有自由意志,即便是有,它也不会表现出来。因此,上面提到的两个因素,对于确保自由意志的存在,是缺一不可的。
7、超宇宙 超宇宙是一种垂直结构的多元宇宙(可被称为“垂直宇宙”),相对于来自量子力学的多世界解释的“平行宇宙”而言。
(2005年2月20日)
二、相似力学
超广义相对论,基于“同真”和“共存”两条原理,统一了三个世界:“客观物质世界”、“主观精神世界”和“计算机虚拟世界”,给出了自然的一个新图景:虚拟世界网,称作“超宇宙”。然而,对于超宇宙中的一个具体节点,即一个宇宙(世界),特别是我们所在的这个世界中的规律,却没有一个统一的认识,因而是不完备的。不同宇宙间的物理规律可以是不同的,那么一个特定宇宙中的物理规律就应该是相同的。基于这个想法,我们提出了“狭义超广义相对论”,它是超广义相对论的一个特例。它是把超广义相对论的原理应用到超宇宙的一个具体节点,即我们这个世界而得到的物理理论。它致力于解决不同观测尺度上的物理规律的统一性问题,因此,也叫“尺度相对论”。
基本原理与物质结构
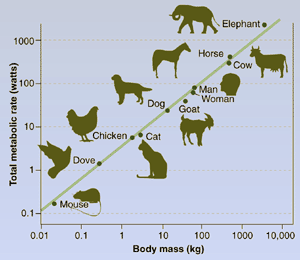
度量的相对性 我们一切关于数量多少的概念都来源于度量。度量是一个比较的过程,即拿一个单位测度作为标准(参照),拿它去和被观测对象比,由含它的多少,来确定被观测对象的数量。度量中,总是拿一个标准作为参照的性质,称作“度量的相对性”。这里的“度量”,包括空间度量、时间度量、速度度量和能量度量。“度量的相对性”即是指,(空间)大小、(时间)长短、(运动)快慢和(能量)高低都是相对的。人体比泰山小,却比蚂蚁大;人的寿命不如乌龟的寿命长,却比苍蝇的寿命长得多;人比蜗牛跑得快,但却赶不上猎豹的速度;人比兔子更有力气,却推不动大象。上面这些例子都说明了大小、长短、快慢和能量的高低都是相对的。所谓“尺有所短,寸有所长”,关键在于比较对象,或说“观察尺度”。
由“度量的相对性”可以推出宇宙物质的无限可分的结构,推理过程如下:因为,度量是相对的,所以,不存在绝对的“大”和“小”;如果宇宙的物质结构不是无限可分的,那么必然存在绝对的“大”和“小”,从而与度量的相对性矛盾;故此,宇宙的物质结构是无限可分的。
基本原理
1、狭义同真原理(同律原理):一切尺度遵守相同的物理规律;
2、狭义共存原理(统计原理):宏观状态与微观状态共存。
由上面的“度量的相对性”,得到了宇宙无限可分的物质结构。那么处于不同尺度上的物质结构及其遵循的物理定律又有什么关系呢?“同律原理”告诉我们,不同尺度上的物质结构是相似的,因为它们遵循着相同的物理规律。由此可知,以人存在的尺度为中心,向上有无数个“大人世界”,其中,以太阳系为原子的那个“大人世界”,是大尺度方向上,离我们最近的“大人世界”,以后,所提到的“大人世界”,如无特别说明,则指离我们最近的那个大人世界。同理,向下有无数个“小人世界”,其中,以原子为太阳系的那个“小人世界”,是小尺度方向上,离我们最近的“小人世界”,以后,所提到的“小人世界”,如无特别说明,则指离我们最近的那个“小人世界”。因此,宇宙的物质结构是一个无限可分的分形结构。
由分形结构的“自相似性”可知,任何层次的“微观粒子”,都是类似太阳系或叫原子的“有核绕转”结构。在空间尺度缩放的同时,时间尺度也在缩放,也就是说,“小人世界”中的时间单位,比我们这个世界中的时间单位要短,而“大人世界”中的时间单位,比我们这个世界中的时间单位要长。但是,空间尺度缩放的比例与时间尺度缩放的比例是不同的,因此,各尺度世界中的光速也就是不同的。设我们这个世界中的光速是c,则“小人世界”中的光速就是[math]\displaystyle{ c^2 }[/math],称为“快光”,而“大人世界”中的光速就是[math]\displaystyle{ \sqrt{c} }[/math],称为“慢光”。
然而,大人世界中的人们,并不觉得“慢光”慢,我们所谓“慢光”,是相对于我们这个世界中的光速来说的,而对于大人世界而言,因为其中的一切过程都放慢了,因此,“慢光”在他们的那个世界中仍是最快的。同样,小人世界中的人们,也不觉得“快光”快,因为,在他们的世界中,一切过程都加快了。对某一尺度而言,其中的光速,是该尺度上的最大信号速度,从而导致了该尺度上“相互作用的局域性”。
狭义共存原理(统计原理)则表明存在两个描述物理现象的尺度,一个宏观尺度,一个微观尺度。且存在一个尺度变换,可以把微观状态的描述变换到宏观状态。因此,狭义超广义相对论,又叫“尺度相对论”。
四种相互作用的统一
20世纪30年代以来,人类对微观物质世界的探索前沿已经推进到了粒子物理领域。六十年代初期,随着大型加速器的建造和探测技术的发展,实验上发现了大量的新的“基本粒子”。到那时,共有五种“力”进入了人们的视野:静电力、磁力、引力、强核力和弱核力。在这些力中,静电力和磁力已经被法拉第/麦克斯韦等人的工作统一为电磁力4;电磁力与弱核力又通过量子电动力学、费曼规则和重正化等手段被统一为电弱力5(由格拉肖、温伯格、萨拉姆等人的工作完成);沿着类似的方向,在量子色动力学(QCD)中,人们建立和发展了强子结构理论,连同电弱统一理论,形成了粒子物理的标准模型6-8。
标准模型认为自然界中存在四种基本相互作用:强(力程1fm,相对强度1)、弱(力程<[math]\displaystyle{ 10^{-3} }[/math]fm,相对强度[math]\displaystyle{ 10^{-12} }[/math])、电磁(力程∞,相对强度[math]\displaystyle{ 10^{-2} }[/math])和引力(力程∞,相对强度[math]\displaystyle{ 10^{-37} }[/math]),和三种基本粒子:规范玻色子(自旋为1)、费米子(自旋为1/2)、希格斯粒子(自旋为0)。大统一理论(GUT)就致力于统一这些不同存在尺度上的各种相互作用和粒子;弦论、膜论和超引力理论等就是它的一些典型代表8。然而,这些相互作用真的可以统一吗?又如何统一呢?
平方反比律。相互作用的形式是由空间的维数决定的。三维空间中唯一合理的作用形式是平方反比作用。证明如下:
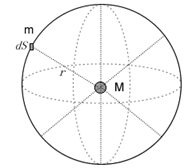
图 6 平方反比力是“媒介子流”面密度下降的结果。球面的面积为:[math]\displaystyle{ 4\pi{r^2}\propto{r^2} }[/math],随着[math]\displaystyle{ r^2 }[/math]增长,因此,“媒介子流”的面密度随着[math]\displaystyle{ r^2 }[/math]下降。所以,三维空间中正比于“媒介子流”面密度的相互作用,必是平方反比的。
如图6所示,设两个物体M与m之间的相互作用力,是通过彼此交换“媒介子”而实现的;物体发射和接收“媒介子”的能力正比于其物质的含量;物体所受到的作用力正比于它所接受到的“媒介子”数。
那么,由物体M发射的“媒介子流”,在三维空间中均匀扩散,其前锋是一个球面。因此,“媒介子流”前锋球面的表面积随着扩散距离r的平方而增大,造成“媒介子流”在其上的面密度,随着扩散距离r的平方而减小。所以,单位物质的量,所接受到的“媒介子”的数目,也就随距离的平方而减小,于是就有:
[math]\displaystyle{
F=K\frac{Mm}{r^2}
}[/math] (a)
这正是平方反比力公式的形式,其中,K是比例常数。
狭义超广义相对论中的一个重要观点就是,物理定律的形式是由空间的维数决定的。上述推导过程中,应用了三个原则:(1)局域性原则,即在各尺度上,相互作用都是局域的,是通过交换有限速度的“媒介子”实现的,不存在瞬时的超距作用;(2)简单性原则,即,作用的强度正比于物质含量的一次方;(3)对称性原则,即,空间中的各方向是对称的,空间是各向同性的。在三维空间中,满足这三个原则的作用力公式,只有平方反比作用式(a)。同理,在二维空间中,满足此三原则的作用力公式,必是一次方反比式,而四维空间中的则是立方反比公式,依此类推。
引力和电磁。 它们都是平方反比作用,是同一种力在不同尺度上的表现,因而是相对的。我们所谓“引力”,对于大人来说就是电磁力;而我们所谓电磁力,对于小人来说,就是引力。因此,可以预言,必有反引力(斥力)存在。由物质组成的星系与由反物质组成的星系,必是互斥的,因而,我们的太阳系才没有和反物质组成的太阳系,相互吸引、碰撞乃至湮灭。对于大人来说,太阳相当于原子核,行星相当于电子。行星在绕太阳运转的轨道间发生跃迁时,会发射慢光波,它是大人世界里的光波,它的速度为[math]\displaystyle{ \sqrt{c} }[/math](设为我们这个世界中的光波)。类似地,在小人们看来,原子核就是太阳,电子就是行星。电子与核子之间的通讯,类似于太阳光照射到地球上来,因此,电子与核子间的通讯靠的是“快光”,即小人世界中的光。
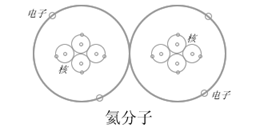
强相互作用与弱相互作用。它们本质上都不是相互作用,而是“反应”。因为强弱相互作用只在核反应和粒子衰变反应中出现,可见它们的本质都是“反应”,正如化学反应一样。因为三维空间中只存在平方反比作用,因此,强弱相互作用的“短程”性质,正表明它们不是相互作用。以往认为它们具有和引力与电磁平等的地位,是自然界中的“基本相互作用”的认识,是错误的。它们的“短程力”性质,更像化学反应,而不是相互作用。正如两个原子化合生成分子时,需要它们彼此接近,只有当在它们外围旋转的电子轨道彼此重合时,它们才能发生反应一样,两个核子发生反应的距离也在核子半径的水平上。即只有当绕核子旋转的“核电子”的轨道发生重合时,核子才发生核反应(见图2)。正如我们不把化学反应认为是基本相互作用一样,我们也不该把核反应和粒子衰变反应当成基本相互作用。粒子表与元素周期表的类比,更加确认了强弱相互作用的“反应”本质。
图7 氦原子的“核中核”结构示意图。
综上可知,三维空间中只存在一种基本相互作用(interaction),即平方反比相互作用,它是长程力。而一切短程“相互作用”,本质上都是“反应”(reaction)。在相互作用中,费米子是作用的主体,玻色子是媒介,而希格斯粒子不存在。
相对论与量子力学的统一
相对论与量子力学作为二十世纪物理学大厦的两大支柱,在各自的应用领域中取得了辉煌的成就,然而它们之间却存在着深刻的矛盾。这矛盾主要体现在两点上:(1)确定性与随机性。相对论是严格的确定论,爱因斯坦顽固地坚持“上帝不掷色子”,而量子则表现出某种固有的随机性(uncertainty),比如海森堡的不确定关系。(2)局域性与非局域性。相对论是严格局域性的理论,认为存在最大的信号传播速度,而量子中则表现出非局域的关联(non-local correlation),比如纠缠态(entanglement)。
这种针锋相对的矛盾深深地困扰着物理学家,以至于不少人认为,它们之中必有一个是错的。然而真是这样吗?这里我们将说明,相对论与量子力学之间看似深刻的矛盾,其实只是表面的,它们本质上可以在狭义超广义相对论的概念框架下统一起来。
先从量子力学的测不准效应说起。这里之所以称其为“测不准效应”而不是“不确定原理”,是想强调,它只是一种观测效应,而不是什么原理。正如“尺缩钟慢”是一种“运动相对性”效应一样,测不准只是一种“尺度相对性”效应。
我们测不准电子的位置,但却可以精确地测定行星的轨道。这一事实启示我们,测得“准”与“不准”取决于观测者与被观测对象之间的相对尺度。由此可以推知,对于小人世界中的人们而言,因为在他们看来,电子就像行星一样大,所以他们完全可以测准电子的轨道,就像我们可以测准行星的轨道一样。同样,我们地球的轨道,对于大人世界中的人们来说,就像电子轨道一样测不准。因而,测不测得准,是相对的,从而,确定性与随机性是一对相对的概念,不存在绝对的确定与随机,就像不存在绝对的静止与运动一样。故,量子力学的随机性并不和相对论的确定性相矛盾,而恰恰是一种“尺度相对论”效应。
再看局域性与非局域性。它们也是相对的。如前所述,两个相对静止的粒子(比如电子和质子)之间的通讯靠的是“快光”,即小人世界中的光。因此,在我们这个世界看来,存在非局域关联的两个粒子,在小人世界看来,它们之间的相互作用仍是局域的。我们之所以认为这种关联是非局域的,是因为联系它们的媒介子的速度,超过了我们这个世界中的光速,而小人们之所以认为它们之间的联系是局域的,是因为联系它们的媒介子的速度,并没有超过小人世界中的光速。
类似地,我们这个世界中的局域相互作用,在大人世界看来,可能就是非局域的。
正是由于在不同的尺度上,最大的信号速度是不同的,所以,在某个尺度上看来是非局域的相互作用,而在一个更小的尺度看来,可能就是局域的;同样地,在某个尺度看来是局域的相互作用,而在一个更大的尺度看来,可能就是非局域的。
因此,局域与否,是相对的,不存在绝对的局域与非局域正如不存在绝对的运动与静止一样。故,量子力学的非局域性并不和相对论的局域性相矛盾,而恰恰是一种“尺度相对论”效应。
再来看看量子的另外一种表现形式:离散。“离散”和“连续”是一对相对的概念。即在某个尺度看来是离散的现象,在另一个尺度看来可能就是连续的;反之亦然。比如,柏油路面在蚂蚁看来是崎岖不平的,但对于汽车轮胎而言却是光滑平坦的。离散现象,只在特定的尺度上才能观察到。对于更大的尺度而言,会因为仪器的分辨率不够,而观察到连续;对于更小的尺度而言,会因为间隔的跨度过大(超过了那个尺度上的人类史),而无法被观察到。因此,没有绝对的离散和连续,就像没有绝对的静止和运动一样。离散和连续的差异是一种“尺度相对论”效应。
超光速的问题 每一个存在尺度,都有一个最大信号传播速度,那就是该尺度上的光速。对于该尺度而言,光速是不可超越的,然而对于更小的尺度而言,有更快的光速(快光)存在。尺度越小,其中的光速就越快。因此,能否超光速,是相对的。每个尺度都无法超越自身的光速,然而,对于比它更小的尺度而言,该尺度上的光速却不构成障碍。光速最大也只是一种“尺度相对论”效应。
最小作用量子的问题 普朗克常数规定了我们这个世界的最小作用量子。然而由于度量的相对性,对于更小的和更大的尺度而言,它都不是最小的作用量子。尺度越小,能量密度越高。因此,最小作用量子只具有相对的意义,它只在特定的尺度上有意义,它的存在,不能据以否定物质无限可分的结构。
物质波的本质
物质波是什么?波函数又是什么?对量子力学中物质波和波函数本质的理解,也一直是困扰物理学家的一个难题。这里我们将给出答案。物质波的本质是“有核绕转”体系位置中心在三维空间中的运动轨迹,是位置中心的一种波动,同时也是体系作用量的波动。波函数则是人为构造的描述“有核绕转”体系作用量波动性的经验公式,是在希尔伯特空间(构型空间)中对“有核绕转”体系作用量波动的一种近似描述。它的模平方反映的是,某时刻的空间某位置到“有核绕转”体系位置中心的距离,正比于在该处发现“有核绕转”体系的概率。
证明如下:
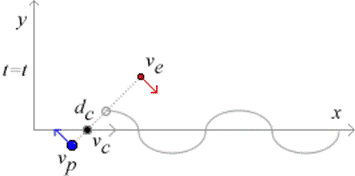
图 8 运动的“有核绕转”体系位置中心的轨迹是波。
如图所示,设有自由的“有核绕转”体系(自由粒子),它不受外力作用,只存在核与外围粒子间的平方反比吸引力,那么,该体系将绕它们共同的质心旋转。设,体系质心具有速度[math]\displaystyle{ v_c }[/math],则在整个运动过程中,体系的动量、能量以及绕质心旋转的角动量均守恒。设,核与质心的距离为[math]\displaystyle{ d_F }[/math],外围粒子与质心的距离为[math]\displaystyle{ d_e }[/math],则,核与外围粒子间的距离为[math]\displaystyle{ d=d_F+d_e }[/math]。设,体系绕质心旋转的角速度为[math]\displaystyle{ w }[/math],核绕质心旋转的线速度为[math]\displaystyle{ v_F }[/math],外围粒子绕质心旋转的线速度为[math]\displaystyle{ v_e }[/math],则有[math]\displaystyle{ w=\frac{v_F}{d_F}=\frac{v_e}{d_e} }[/math]。以质心的运动方向为x轴正方向,建立坐标系,则质心的纵坐标y恒为0。体系的位置中心是核与外围粒子间连线的中点,简称“位心”。设,体系“位心”到其质心的距离为[math]\displaystyle{ d_c }[/math],则有,[math]\displaystyle{ d_c=\frac{d_e-d_F}{2} }[/math]。设,体系外围粒子的质量为[math]\displaystyle{ m_e }[/math], 核的质量为[math]\displaystyle{ m_p }[/math],且[math]\displaystyle{ m_p=km_e=km }[/math]。试求“有核绕转”体系位置中心的运动轨迹。
解:设外围粒子的坐标为[math]\displaystyle{ x_e(t) }[/math]和[math]\displaystyle{ y_e(t) }[/math]。因为体系质心的速度[math]\displaystyle{ v_c }[/math]沿x轴正方向,故有,外围粒子的运动轨迹为:
[math]\displaystyle{
\left\{\begin{array}{ll}
x_e(t)=d_ecos(wt)+v_ct&\\
y_e(t)=d_esin(wt)
&\end{array}
\right.
}[/math] (28)
设核的坐标为[math]\displaystyle{ x_p(t) }[/math]和[math]\displaystyle{ y_p(t) }[/math]。则有,
[math]\displaystyle{
\left\{\begin{array}{ll}
x_F(t)=-d_Fcos(wt)+v_ct&\\
y_F(t)=-d_Fsin(wt)
&\end{array}
\right.
}[/math] (29)
由(28)和(29),可得体系位置中心的坐标为:
[math]\displaystyle{
\left\{\begin{array}{ll}
x_c=\frac{1}{2}(x_e+x_F)=\frac{1}{2}(d_e-d_F)cos(wt)+v_ct&\\
y_c=\frac{1}{2}(y_e+y_F)=\frac{1}{2}(d_e-d_F)sin(wt)
&\end{array}
\right.
}[/math] (30)
把[math]\displaystyle{ d_c=\frac{d_e-d_F}{2} }[/math]代入(30),得,
[math]\displaystyle{
\left\{\begin{array}{ll}
x_c(t)=d_ccos(wt)+v_ct&\\
y_c(t)=d_csin(wt)
&\end{array}
\right.
}[/math] (31)
这就是“有核绕转”体系位置中心运动轨迹的参数方程。
由(31)可知,若体系两部分的质量相等,则体系的位心与质心重合,[math]\displaystyle{ d_c }[/math]等于0,从而,体系不表现波动性;反之,若体系两部分的质量不相等,则体系的位心与质心不重合,[math]\displaystyle{ d_c }[/math]不等于0,从而,体系位置中心的轨迹就是波。一般而言, “有核绕转”体系的质量大部分集中在核上,因此,位心与质心不重合,从而体系的位置中心就会表现出波动性。
不确定关系。体系两部分间的距离d,是体系在位置空间中的跨度,表征了体系位置的不确定度;体系两部分间的相对速度v=wd,是体系在速度空间中的跨度,表征了体系速度的不确定度。而将速度不确定度乘以体系的质量,就得到体系动量的不确定度。由于整个运动过程中,体系的角动量守恒,根据角度动量的定义有,
[math]\displaystyle{
L=mwd^2=d\cdot{mwd}=\Delta{r}\cdot\Delta{p}=constant
}[/math] (32)
可见,位置不确定度和动量不确定度之间存在着此消彼长的反比关系,即,位置的不确定度越小,则动量的不确定度越大,反之亦反;而这正是海森堡不确定关系的含义。由此可知,不确定关系是体系角度量守恒的结果。
换个角度看,也是体系能量守恒的结果。因为,体系的内力是保守吸引力,所以,体系两部分间的距离越大(位置不确定度越大),则体系的势能比重越高,动能比重越低(动量不确定度越小),反之,体系两部分间的距离越小(位置不确定度越小),则体系的势能比重越低,动能的比重越高(动量不确定度越大)。
总之,体系的动量不确定度和位置不确定度之间存在此消彼长的关系。
熟悉如何从波函数推导出不确定关系的读者,应该能够体会到此处推导的简明性。从波函数推导出不确定关系是一个冗长晦涩的过程9,而对于不确定关系起因的解释10,更是千奇百怪,莫衷一是。就拿海森堡自己所给出的“正宗”解释来说,也带有浓重的主观唯心主义色彩,比如,他认为不确定来源于测量仪器对待测体系的干扰。后来,他的解释被人演义成主观意识因素所起的作用,彻底陷入主观唯心主义。
由上面的推导可以看出,不确定关系是自由的“有核绕转”体系角动量(或说能量)守恒的必然结果,推导过程简单且物理意义明确。
体系作用量的波动 由(31)对t求导,可得体系位置中心的速度[math]\displaystyle{ v_g }[/math]为:
[math]\displaystyle{
\left\{\begin{array}{ll}
v_{g_x}=-d_cwsin(wt)&\\
v_{g_u}=d_cwcos(wt)
&\end{array}
\right.
}[/math] (33)
则体系位置中心的作用量为:
[math]\displaystyle{ S_c=\vec{p}\cdot\vec{r}-E\cdot{t}=m_c\vec{v_g}\cdot\vec{r_g}-E\cdot{t}=m_c[v_{g_x}r_{g_x}+v_{g_y}r_{g_y}]-\frac{1}{2}m_cv_c^2t =m_c[(-d_cwsin(wt)+v_c)(d_ccos(wt)+v_ct)+d_c^2wsin(wt)cos(wt)-\frac{1}{2}v_c^2t] =m_c[d_cv_ccos(wt)+d_cv_cw(1-t)sin(wt)+\frac{1}{2}v_c^2t-\frac{1}{2}d_c^2w^2] }[/math] (34)
其中,[math]\displaystyle{ m_c=(k+1)m }[/math],是体系的总质量。
由(34)式可见,体系的作用量[math]\displaystyle{ S_c }[/math]是随时间t波动的。而薛定谔波动方程所描述的自由粒子的波函数为,
[math]\displaystyle{
\psi(r,t)=Ae^{pr-Et}=Ae^{S}
}[/math] (35)
比较(34)和(35)就会发现,薛定谔波动方程所描述的波函数是在希尔伯特空间中对“有核绕转”体系作用量波动的一种近似。薛定谔建立波动方程的初衷是为了用新的观点(波动的观点)来研究原子的结构。他拿自由粒子和平面波作类比,人为地引入一个虚指数函数,使自由粒子的作用量波动起来,从而以类似驻波的概念解释了原子结构的稳定性。而由此付出的代价就是,把原本物理意义明确的3维实空间中的波动引到了神秘莫测的复空间中。至于(35)中的普朗克常数,则反映了我们当前观测水平下,仪器所能达到的分辨率。我们现在认清了物质波动的本质和来源之后,原则上,就不再需要那个人为引入的复函数了。然而,作为一套经验公式,量子力学的公式体系在处理某些实际问题时仍有一定的使用价值。
距离函数 方程(31)是“有核绕转”体系位置中心运动轨迹的参数方程。对于一个确定的时刻t,它给出了“有核绕转”体系在空间中的平均位置。据此,我们可以定义距离函数如下:
[math]\displaystyle{
d(x,y,t)=\sqrt{(x-x_c)^2+(y-y_c)^2}
=\sqrt{(x(t)-d_ccos(wt)+v_ct)^2+(y(t)-d_csin(wt))^2}
\approx\propto{1-|\psi(x,y,t)|^2}=1-\psi\prime\psi
}[/math](36)
它表示在t时刻的空间某位置(x, y)处到“有核绕转”体系位心的距离,反映了在该处发现“有核绕转”体系的概率,而这个概率,约正比于薛定谔方程中波函数的模平方。
“有核绕转”体系的位心代表了体系整体的位置,方程(31)表明,在t时刻,体系的位心有一个确定的位置,在空间位置(x, y)处发现体系的概率负比于该位置到体系位心的距离。因为,距离的远近是相对的,所以波函数的模平方放大一个倍数(相当于改变距离的度量单位),不会改变在空间某位置处发现体系位置中心的概率,因此,波函数可以被归一化。
由此可见,距离远近的相对性是量子力学波函数可以被归一化的基础,而距离函数则是波恩几率诠释的对象的实质。此外,还需注意,位心毕竟是位心,它只在平均(统计)的意义下给出“有核绕转”体系整体的位置。事实上,在位心处,既没有核,也没有外围粒子。因此,通过“有核绕转”体系的位置中心来整体地把握体系的运动(就像我们这个尺度上的人们做微观物理实验时那样),得到的终归还是一个统计结果。
以氢原子为例,我们做实验可以观测到氢原子的波动性,是因为在我们的观测尺度上,是通过氢原子的位置中心来整体地把握氢原子的运动的。然而,对于小人世界中的人们来说,他们不会通过氢原子的位心来把握氢原子的运动,因为,在他们看来,氢原子就像太阳系一样大,所以他们会直接确定质子和电子的位置,就如我们直接确定太阳和地球的位置一样。因此,他们得到的并不是统计结果。即,是否得到统计结果,是相对的。我们观测到统计结果是一种“尺度相对论”效应。
德布罗意关系、薛定谔方程和波恩诠释 物质波的概念最早是由德布罗意在1924年提出的11。他受光子波粒二象性的启发,猜测物质粒子可能也有波动性。他的想法在1927年被戴维逊和革末的电子衍射实验所证实12。德布罗意物质波概念的提出作为成功运用类比思维的例子,被物理学界传为佳话。德布罗意通过类比建立了著名的德布罗意关系式:
[math]\displaystyle{ \lambda\cdot{p}=h }[/math](37)
将(37)和(32)作一比较就会发现,德布罗意关系实际上是不确定关系的另一种表述形式。换言之,它和海森堡不确定关系本质上是一回事儿。它们都是“有核绕转”体系角动量和能量守恒的结果。
薛定谔方程是薛定谔在1926年建立的13。他也是运用类比思维的结果。薛定谔拿自由粒子的运动和平面波的传播作类比,建立了以他的名字命名的波动方程。波函数的概念便由此而来。然而,从直接意义上看,薛定谔波动方程中的波与德布罗意关系中的波不是同一个波。比如,德布罗意关系中所给出的波长具有长度的量纲,有直接的物理意义。而薛定谔波动方程中的波,因为是复空间里的波动,其波长就没有直接的物理意义。由此可见,德布罗意关系中的波与薛定谔方程中的波,从直接意义上看,不是同一个波。薛定谔方程中的波实际上是人为构造的“有核绕转”体系作用量波动的经验公式。
波恩对波函数的解释14,称为“哥本哈根”正统诠释。然而,波恩所解释的波,是一种几率(幅)的波动,从直接意义上看,它既不同于德布罗意关系中的波(波长具有长度量纲的波动),也不同于薛定谔方程中的波(复空间中作用量的波动)。波恩所解释的几率实际上反映的是空间某处到“有核绕转”体系位置中心的距离。正是由于波恩的解释才引出了波函数归一化的问题。实际上,单纯地看德布罗意关系中的波,或是薛定谔方程中的波,都不需要归一化。因为,德布罗意是通过与光波类比建立关系式的,就像光波不需要归一化一样,德布罗意物质波,也不需要归一化。同样,薛定谔是通过和普通平面波(比如机械波或者电磁波等)类比建立方程的,所以,薛定谔波动方程中的波,就像平面波一样,不需要归一化。然而,在没有认识到物质波动性来源(即没有认识到微观粒子“有核绕转”结构的普遍性)的时候,为了统一地理解波粒二象性,波恩才提出了波函数的几率解释,于是才引出了波函数的归一化问题。
综上可知,从直接意义上看,德布罗意关系中的波、薛定谔方程中的波和波恩几率诠释中的波,这三个波,含义各不相同。但是,它们本质上又是从不同的侧面对同一种波,即“有核绕转”体系位置中心波动的反映。德布罗意关系反映的是“有核绕转”体系角动量(或能量)的守恒性,薛定谔波动方程反映的是“有核绕转”体系作用量的波动性,而波恩解释反映的则是某时刻空间某处到“有核绕转”体系位置中心的距离。
波粒二象性 从上面的推导可知,“有核绕转”体系运动起来之后,就会自发地表现出整体(位心)的波动性(波的本质就是周期性的传播)。反过来,能够在运动中自发地表现波动性的物体,也一定是“有核绕转”体系。电子在原子中的轨道上,表现出类似驻波的性质,由此,可以推知电子也是“有核绕转”体系。推而广之,所有微观粒子(玻色子除外,解释见后)都是“有核绕转”体系。
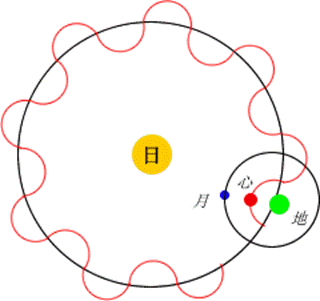
再与太阳系做个比较,地球绕着太阳转,月亮绕着地球转。地月质量之比约为80:1,地月体系的位心与质心不重合,那么,地月位心的轨迹必是盘绕在地球质心轨道周围的驻波(如图9所示)。此外,太阳系由10来颗行星组成,由此可以推测太阳本身可能也不是一个单一的球体,它可能是由十几二十个小球融合而成的复合球体(像原子核那样),那么这个复合球体的特征,应该可以在太阳的活动中表现出来,比如太阳黑子可能就是这些小球间的缝隙,而水星在近日点的进动可能就是这个复合球体的密度不均匀性造成引力不均的结果。
图 9 地月位心轨迹的示意图。
物质波的本质是“有核绕转”体系位置中心的波动,它很好地体现了波动性与粒子性的统一:一方面,位置中心在运动中自发地表现出波动性;另一方面,在一个确定的时刻位置中心又有一个确定的位置,因而表现出了整体的粒子性。然而,如前所述,位心毕竟是位心,它只在平均(统计)意义上代表粒子整体的位置。因此,整个粒子只是在统计意义上,有确定的位置而已,因此,实验得到的仍是统计结果。
认清了物质波和波函数的本质,我们就可以对各种各样的对波函数的解释,做出评价了。下面仅就有代表性的两个观点做出评述。一个是薛定谔的波包解释,它过分地强调了波动性的一面,面临波包扩散的难题,而由位心波动可知,由于“有核绕转”体系内部存在相互吸引作用,所以体系是不会扩散的。另一个是爱因斯坦的统计系综解释,它过分地强调了粒子性的一面,认为物质波是大量粒子聚集、相互影响而表现出来的一种集体行为,而实际上,物质波的本质是一种合成运动(转动与平动的叠加运动),是(“有核绕转”结构的)单个粒子就能表现出来的波动性,是粒子固有的波动性,并不依赖于大量粒子的聚集。因此,上述两种解释,各执一偏,不中肯綮。
正如前面所说,由于度量的相对性,这种波动性是否显著也是相对的。对于小人们来说,电子大如行星,因而他们不关心电子的波动性。同理,对大人们来说,我们的地球小如电子,而我们的太阳系,也不过是一个原子。因此,如果大人造一个巨大的光栅,取一束太阳系照射过去,也可以观察到太阳系们的衍射现象。由此可知,波动性与粒子性是相对的,它们不过是一种“尺度相对论”效应而已。
尺度变换、对称破缺、不确定性与时间之矢 有了前面物质波的讨论,现在可以具体地说一下尺度变换了。“尺度变换”,其实很简单,就是一个求统计平均(求和)的操作过程。因为,求和运算是个多对一的映射,因此,是个不可逆的过程,对称性便由此破缺,随机性便由此产生。道理很简单:我们知道1 + 1 = 2,但是,若问你2等于几,答案却不一定是1 + 1,因为,1.5 + 0.5也等于2,0.8+1.2也等于2。可见,知道两个数可以唯一地确定它们的和,而知道一个和却不能确定它原来的两个加数。物质波的本质是一个很好的例子,可以用来说明,随机性正来源于尺度变换。
由“狭义共存原理”可知,存在两个描述物质运动状态的尺度:微观尺度和宏观尺度。从微观尺度上,可以直接描述“有核绕转”体系各部分的运动,并不需要以位心近似的方式去描述整体,从而不出现不确定性。然而,如果由于尺度的原因,不得不从宏观的尺度以位心近似的方式整体地把握“有核绕转”体系的运动时,我们就不得不进行统计平均——求位心——(这通常由我们的测量仪器自动完成,我们一般不需要显式地做这件事),这是一个不可逆的单向物理过程,因为,知道“有核绕转”体系两个部分的位置可以唯一地确定它的位心,而反过来,知道体系的位心,却无法确定它的两个部分的位置,随机性就由此产生了。
时间之矢的概念在近些年,被不少人讨论过,如霍金在《时间简史》6、普里高津在《确定性的终结》15等。时间箭头本是一个简单的事实,因为,我们每个人都能感觉到时间一去不复返的单向性。我们总是从昨天到今天再到明天地这么过着。可时间为什么是单向的呢?这个问题似乎就不是那么简单了。要得到此问题的答案,需要从物理过程的可逆性说起。物理过程的可逆性又与支配物理过程的物理规律的确定性有关。如果物理规律是确定的,就像牛顿定律一样,那么原则上物理过程是可逆的。由于牛顿力学的成功,18世纪曾流行一种机械的世界观,认为宇宙是一架巨大的钟表。拉普拉斯就曾认为,如果给定某个时刻所有粒子的位置和动量,他就能准确地算出宇宙的过去和未来,于是,时间在他眼里便如无物。后来,热力学的出现和发展,似乎为时间的单向性找到了原理性的解释,那就是热力学第二定律,即熵增原理。如果把宇宙看成一个孤立的系统(这似乎是合理的,因为宇宙被定义成这个世界中的一切,那么根据定义,宇宙之外就不该再有东西存在,如果还有,就可以把它划归到这个宇宙中来,因此,认为宇宙是个孤立系统,听起来是合理的),那么熵增原理中熵变化的单向性,就是时间单向性的物理根据。然而,这只是一种简单的对应,并没有说明时间单向性的原理,更加没有说明熵何以增加。
这里将说明,熵增加和时间之矢正是来自于尺度变换。众所周知,熵是系统微观状态数的度量,而熵增原理的应用依赖于充分大的随机性,即所谓的“各态历经”。如前所述,随机性正来源于尺度变换,而这正是熵增原理得以应用的前提,而且熵增原理也只有在宏观尺度上描述微观体系时才用得着。如果,你可以直接在微观状态下,观测和控制体系的运动(如麦克斯韦妖的本领),那么,熵对你而言就是一个无用的概念(注:如果你不再深究更微观的尺度的话),而且一切过程对你而言都是可逆的,因此,你的眼中也不会有单向的时间。
综上所述,物理过程没有绝对的可逆与不可逆,物理现象也没有绝对的确定与随机,它们的差异取决于观测的尺度。我们观测电子的运动是随机的,但是在小人们看来,电子的运动(包括轨道和动量)就是完全确定的。故此,时间可不可逆也是相对的,时间的单向性是一种“尺度相对论”效应。
场的本质
场是什么?场就是“媒介子流”,而力线就是对媒介子流轨迹的直观描述。
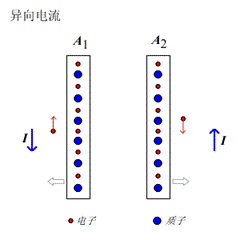
磁场是什么?磁场是电场的一种“运动相对论”(爱因斯坦的狭义相对论)效应,是空间收缩而引起的一种观测效应。
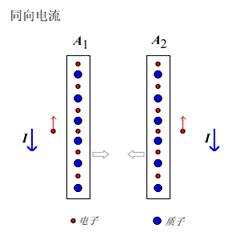
如图10所示,设A1中的质子和A2中的质子之间的相互作用力为[math]\displaystyle{ F_{F1}^{F2} }[/math],电子间的作用力为[math]\displaystyle{ F_{e1}^{e2} }[/math],A1中的质子和A2中的电子之间的作用力为[math]\displaystyle{ F_{F1}^{e2} }[/math],A1中的电子和A2中的质子之间的相互作用力为[math]\displaystyle{ F_{e1}^{F2} }[/math],则,
[math]\displaystyle{
F_{yin}=F_{F1}^{e2}+F_{e1}^{F2},F_{chi}=F_{F1}^{F2}+F_{e1}^{e2}
}[/math] (38)
图 10 导体A1和A2通以同向电流时,它们相互吸引,而通以异向电流时它们互相排斥。
在通电流之前,由于两导体中带有等量的正电荷与负电荷,所以有,
[math]\displaystyle{
F_{F1}^{e2}=F_{e1}^{F2}=F_{F1}^{F2}=F_{e1}^{e2}
}[/math] (39)
因此,
[math]\displaystyle{
F_{yin}=F_{chi}
}[/math] (40)
在通上电流之后,两导体中的电子发生了定向运动(不妨设两导体中的电流大小相同)。
先看,同向电流时的情形。通以同向电流时,两导体中的质子之间仍相对静止,两导体中的电子之间也相对静止。因此,[math]\displaystyle{ F_{F1}^{F2} }[/math]和[math]\displaystyle{ F_{e1}^{e2} }[/math]都不发生变化,从而两导体间的斥力,[math]\displaystyle{ F_{chi}=F_{F1}^{F2}+F_{e1}^{e2} }[/math],不变,即:
[math]\displaystyle{
F_{repulsive}^{\prime}=F_repulsive=F_{F1}^{F2}+F_{e1}^{e2}
}[/math] (41)
其中,[math]\displaystyle{ F_repulsive^{\prime} }[/math]是通电之后的排斥力。
而导体A2中的电子相对于导体A1中的质子有一个定向的速度,那么由于电量守恒(即电量是个“运动相对性”不变量)和相对论的“尺缩效应”,由导体A1中的质子发射出来并由A2中的电子接收的媒介子流的面数密度看上去增加了,结果便是[math]\displaystyle{ F_{F1}^{e2} }[/math]增加了。下面是一个简明的推导过程。
根据“运动相对论”的尺缩公式,
[math]\displaystyle{
L=L_0\sqrt{1-\frac{v^2}{c^2}}\cong{L_0}(1-\frac{1}{2}\frac{v^2}{c^2})=L_0(1-\frac{1}{2}\beta^2)
}[/math] (42)
有:
[math]\displaystyle{
\Delta{L}=L-L_0=-\frac{1}{2}\beta^2L_0
}[/math] (43)
令
[math]\displaystyle{
L\downarrow=|\frac{\Delta{L}}{L_0}|=|-\frac{1}{2}\beta^2|=\frac{1}{2}\beta^2
}[/math] (44)
则“[math]\displaystyle{ L\downarrow }[/math]”是长度的减少因子。
根据媒介子流面数密度的定义,有:
[math]\displaystyle{
\because{D_a}=\frac{Q}{A}=\frac{Q}{LL_0},L\downarrow=\frac{1}{2}\beta^2
}[/math]
[math]\displaystyle{
\therefore{D_a}\uparrow=\frac{1}{2}\beta^2
}[/math] (45)
其中,“[math]\displaystyle{ {D_a}\uparrow }[/math]”是媒介子流面数密度的增加因子。
因此,
[math]\displaystyle{
F_{F1}^{e2}\uparrow=\frac{1}{2}\beta^2,F_{e1}^{F2}\uparrow=\frac{1}{2}\beta^2
}[/math] (46)
于是
[math]\displaystyle{
F_{attractive}\uparrow=(F_{F1}^{e2}+F_{e1}^{F2})\uparrow=\frac{1}{2}\beta^2
}[/math] (47)
结果有
[math]\displaystyle{
F_{attractive}^{\prime}=F_{attractive}(1+\frac{1}{2}\beta^2)=F_{attractive}+\frac{1}{2}\beta^2)F_{attractive}\gt F_{repulsive}
}[/math] (48)
其中,是通电后的引力。于是我们便观察到两个导体之间的吸引现象,看上去就像它们之间有磁场一样。
其次,我们看两个导体中通以反向电流的情形。此时,两个导体中的质子相对静止,于是,[math]\displaystyle{ F_{F1}^{F2} }[/math]不变。两个导体中电子的相对速度为2v(这里用的是伽利略速度合成公式,因为导体中电子定向运动的速度不是很快),于是,长度收缩因子为
[math]\displaystyle{
L\downarrow=|\frac{\Delta{L}}{L_0}|=|-\frac{1}{2}(\frac{2v}{c})^2|=2\beta^2
}[/math] (49)
于是有:[math]\displaystyle{ F_{e1}^{e2}\uparrow=2\beta^2 }[/math]。
故此,
[math]\displaystyle{
F_{repulsive}^{\prime}=F_{F1}^{F2}+F_{e1}^{e2}==F_{F1}^{F2}+(1+2\beta^2)F_{e1}^{e2}=F_{repulsive}+2\beta^2F_{e1}^{e2}=F_{repulsive}+\beta^2F_{repulsive}
}[/math]
考虑到
[math]\displaystyle{
F_{attractive}^{\prime}=F_{F1}^{e2}(1+\frac{1}{2}\beta^2)+F_{e1}^{F2}(1+\frac{1}{2}\beta^2)=F_{attractive}+\frac{1}{2}\beta^2F_{attractive}
}[/math]
和
[math]\displaystyle{
F_{repulsive}=F_{attractive}
}[/math]
我们得到
[math]\displaystyle{
F_{repulsive}^{\prime}\gt F_{attractive}^{\prime}
}[/math] (50)
于是,我们便观察到两个导体之间的净排斥力,而这一现象通常被解释成两个导体之间存在磁场。
由此可见,磁场是电场的一种“运动相对论”(狭义相对论)观测效应,即“动电生磁”。从来就没有脱离电场而存在的磁场,因此,磁荷和磁单极子是不存在的。
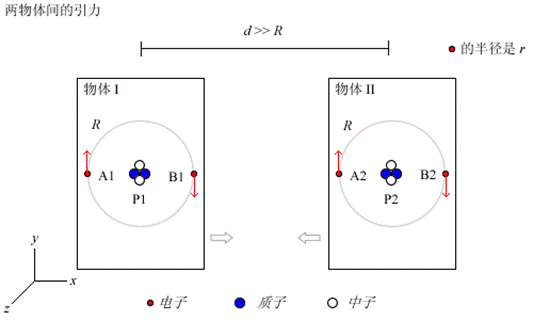
什么是引力?引力是我们周围最普通的一种力。根据爱因斯坦的广义相对论,引力可以看作时空的弯曲16, 17。在2005年,Gupta教授(I.E.T., Lucknow, India)提出了引力的另一解释,即引力是静电力的二阶相对论效应18。下面的图表就是根据Gupta教授的想法绘制的。
图 11 引力场产生机制的示意图。设两物体(物体I和物体II)包含类氦的原子;两物体间的距离d远大于原子的半径R。为简单起见,设两原子(分别位于两个物体中)如图放置,其中,A1和B1是物体I中的电子,而A2和B2是物体II中的电子;物体I中的两个质子合称P1,而物体II中的两个质子合称P2。由于尺缩效应而产生的两个物体中的原子中的电子与质子间的净的吸引(+)与排斥(-)因子如下表。
表 1 由长度收缩效应而带来的、两物体原子中的电子和质子之间的净的吸引(+)与排斥(-)因子
如图11和表1所示,在长度收缩公式中,当考虑洛仑兹速度叠加时,就会出现净的吸引力。牛顿的引力公式可以从库仑静电力公式推导出来:
[math]\displaystyle{
F={1/(4\pi\varepsilon)}\cdot{q_1}[q_2f]/d^2
={1/(4\pi\varepsilon)}(\frac{1}{2}N_Am_1e)[N_Am_2e\cdot{K(v/c)^{\pi_1}(r/R)^{\pi_2}}]
=G\cdot{m_1}m_2/d^2
}[/math] (51)
而引力常数G 的理论估计值为:
[math]\displaystyle{
G={(\frac{1}{2}N_Ae)^2/(4\pi\varepsilon)}\cdot{K(v/c)^{\pi_1}(v/R)^{\pi_2}}
}[/math] (52)
这些公式的详细推导与估算过程,可以参见Gupta的论文18。
据Gupta教授的观点,两个介观物体(比如两个分子)间的、由于电荷分布而产生的范德华力,可以被看作是静电力的零阶相对论效应,即不体现任何相对论效应;“磁力”可以被认为是静电力的一阶相对论效应,因为它体现了狭义相对论的尺度收缩;而两个宏观物体间的相互作用则可以看作静电力的二阶狭义相对论效应,因为它考虑了速度的相对论性叠加(洛仑兹速度变换)。这一观点可以从概念上统一(长程)相互作用,即将长程相互作用统一成静电力及其狭义相对论效应。但这一观点仍有尚未解决的问题,因为两个中子间的相互作用无法用类似解释两个原子间的相互作用的方式去解释,除非认为中子也是具有像原子一样的有核结构。根据狭义超广义相对论,我们知道所有的(实)粒子都有着“有核绕转”结构。这样一来,力就可以统一为平方反比作用和它的狭义(运动)相对论效应,于是就完成了长程相互作用的统一。
质量“真”的增大了吗?物体质量随其速度的增加而增大,是“运动相对论”的一个重要推论。然而真是这样吗?迄今,我们关于质量增加的证据,主要来自加速器实验。在加速器中,发现粒子越来越难被加速,用荷质比公式一算,好像粒子的质量增加了。然而事实如何呢?这要从粒子被加速的原理说起。粒子在外场中被加速,其动量的增加来源于媒介子流对它的冲击力。做个比喻,就像溪流冲滚一块鹅卵石。鹅卵石滚动的速度不会超过溪流的速度。而当鹅卵石滚动的速度越来越快时,它和溪流之间的速度差就会越来越小,溪流对它的冲击力也就越来越小,结果便是它越来越难被加速。如果你认定冲力恒定的话,你就会认为它的质量越来越大。而实际上,它的质量并没有变,只是冲力越来越小的缘故。由此可见,质量和电量一样(它们都是平方反比量),也是个“运动相对论”不变量。
电量和质量 电量和质量本质是同一种物理量,那就是平方反比量,它们是同一种量在不同尺度上的表现。如果物质不是无限可分的,那么,如果电量是分立的,质量也就是分立的。事实上,如前所述,物质是无限可分的,因此,离散和连续是相对的,是一种“尺度相对论”效应。电荷的分立性,是由于我们仪器的分辨率不够造成的。事实上,在量子色动力学中,电荷的分数性质已显端倪,如夸克就被认为具有三分的电荷等。这已经是对原来的电荷整数分立性观点的挑战,相信随着仪器分辨率的提高,终将认识到分立性的相对性。
自旋是什么?自旋就是粒子的“自转”,同时也是“有核绕转”体系中外围粒子的公转。因此,自旋角动量与轨道角动量,是相对的,取决你的观测尺度。在宏观尺度看,是自旋角动量的,换到微观尺度看,可能就是轨道角动量,反之亦反。这就是它们遵从相同的对易关系的原因。自旋作为一种角动量,反映的是粒子的一种“极性”,确切地说,是方向性。我们对于费米子的测量,为什么总是得到自旋只有正负两个值呢?原因是这样的,角动量虽然可以有很多方向,但是作为磁矩耦合到一起时,却只有两种平衡态的排列方式:顺磁和逆磁,前者是稳定平衡,能量较低,后者是不稳定平衡,能量较高,因此,就只能测得自旋的正负两个值。
同位旋是什么?同位旋是在错误的方向上引入的一个错误的概念。它作为一种处于经验阶段的、唯象理论中的概念,其存在有一定的历史意义,但却不能当真,一旦认清物质结构的本质之后,就应该及时摒弃它。
光“真”的存在吗?
这是一个高级话题。据《圣经》中的“创世记”一章记载,上帝创造的第一个事物就是光。上帝说:“要有光”,于是便有了光。然而,光真的存在吗?这要从“玻色子”与“费米子”的区别说起。
费米子和玻色子 量子力学中称自旋为半整数的粒子为费米子,而自旋为整数的粒子为玻色子,因为它们遵循不同的统计规律:玻色子遵循玻色-爱因斯坦统计,而费米子遵循费米-狄拉克统计。费米子和玻色子的一个重要区别,就是是否遵守“泡利不相容原理”。这是一个本质的区别,区分出了粒子的“虚实”。费米子是“实”粒子,因为,只有“实”粒子才会占据空间,才具有排他性,而虚粒子没有。因此,从实体论的角度说,玻色子是不存在的。玻色子总是从一个费米子发出,被另一个费米子吸收,充当的是两个费米子之间的媒介,反映的是费米子之间的联系,它不具有实体论地位。拿男女关系做个比喻,两个费米子好比男人和女人,那么玻色子就是他们之间的“爱情”。爱情是“虚”的,它不具有实体论地位,它不占据我们的三维空间,它仅仅反映两个实体之间的联系。
因此,我们说,作为媒介子的玻色子是虚粒子,它们在三维空间中都是不存在的(不占体积)。从这个意义上说,光是不存在的。一切费米子都是“有核绕转”体系,而玻色子不是。那么,光为什么也会表现出波动性呢?比如,可以发生干涉和衍射。前面不是说过,波动性是“有核绕转”体系结构的反映吗?岂非自相矛盾?
光为何波动? 原因是这样的,光作为一种媒介子反映的是费米子之间的联系,双缝干涉实验也好,单缝衍射实验也好,出现明暗相间的条纹,都是“缝”和“屏”上的费米子相互作用的结果(当然,还包括了光源和你眼睛中的费米子,如果你做观测的话)。因此,光波实验中的波动性,本质上,不是光子的波动性,而是“缝”和“屏”上的费米子的波动性。光的波动性只是一种表象而已,不是本质,它只是一种方便的理解方式,不能当真。另一方面,光作为费米子之间的媒介子,可以把一个费米子的波动性传播到另一个费米子,从而导致费米子之间的相互干涉。类似地,电磁波作为光的等价物,其波动性也是相互作用着的费米子的波动性的反映,不再赘述。
光的本质 “不识庐山真面目,只缘身在此山中”,如果,要认清光的本质,需要超出我们这个世界,到运行我们这个世界的那个模拟器上去看,扮演一把上帝的角色。实际上,超广义相对论已经给了我们扮演上帝角色的视角,我们就到那里去看看吧。我们这个世界运行在一个元胞自动机上,而光就是“上帝”为我们这个元胞自动机设定的邻域更新规则,即,如何由邻近元胞的状态,更新当前元胞状态的规则。
光速为何不变且最大? 认清了光的本质,就可以解释光速为何是不变的了。因为运行我们这个世界的模拟器,作为一个运算系统,执行程序指令,是需要时间的,而且判定当前元胞的邻居的状态,并据以更新当前元胞的状态,需要固定的指令周期,同时,元胞间可以发生影响的距离也是预先设定的,因此,由前者去除后者所得的商,也是固定的,而这个商,就是光速。故此,光速是不变的。又由于状态空间中一切由元胞构成的物体的运动,都是由它(邻域更新规则)驱动的,因此,光也是最快的。因为光只是更新状态的规则,因此,它不占据状态空间。那么它以什么方式存在呢?这就要看下面的“超对称”了。
超对称 超对称是一个伟大的概念。它原本是为了统一“基本相互作用”而提出的。它是想用一个更大的群,把费米子和玻色子都包含进来,即,让玻色子和费米子都成为该群的一个表示。把粒子看成群的表示的思想,是美妙的,是对称性引导物理定律的一个典范。然而,对称性是一把双刃剑,它既可以正确地引导物理定律的发展,也可以误导物理定律的发展,取决于运用是否得当。如果有人试图把所有的化学分子,都看作某群的一种表示,他的做法,和把所有粒子都看成群表示的做法一样的有道理或没道理。但不管怎样,把群表示和基本相互作用的规律联系起来的做法,是没道理的。基本相互作用的规律是由空间的维数决定的,跟群表示无关。但是“超对称”确是一个伟大的概念,如果你意识到它的本质的话。
超对称的实质是程序的代码与数据之间的对称,因为无论是程序代码还是状态数据,都占据计算系统的内存空间,也就是说,从占据内存空间这一点上看,它们是平等的,体现了某种对称关系。因为我们这个世界运行在一个以元胞自动机规则更新的模拟器上,因此,超对称表明了规则与状态之间的对称,从而创造了一个“自在”的开放演化系统。
超对称是荒诞而深刻的,它的荒诞程度不亚于两个量纲不同的物理量相加,而它的深刻程度足以称得上是物理思想的一次革命。超对称不只存在于粒子领域,实际上,在生物学领域也发挥着重要作用:它是生命得以存在和繁衍的基本保证。大家知道,遗传物质是DNA,而DNA是一种双螺旋结构。双螺旋结构的DNA物质,至少包含了两方面的信息:关于生命物质构成的信息和关于生命功能执行的信息。早在沃森和克里克发现双螺旋结构之前,冯诺依曼在能够自我繁殖的机器的设想中,就从逻辑分析出发,提出了生命遗传物质应该包含“构成”和“功能”两方面信息的思想,而这就是“超对称”思想的发轫。关于超对称,在人工宇宙部分再详细讨论。
弦和旋 弦论中把不同的粒子表示成弦的不同的振动模式的想法19,是美妙的,可以作为理论创作的一件艺术品去赏玩,然而,却不能当真,因为它没有坚实的物质基础。相比之下,“有核绕转”结构(以后简称“旋”)是有着坚实物质基础的模型,至少,我们所知的太阳系和原子都是这样的结构。所有(实)粒子(即费米子)都是“旋”的看法,满足尺度变换的不变性,可以统一物质的相互作用。从逻辑上看,物质之间的相互作用不外乎两种方式:通过媒介的相互作用和直接接触的相互作用。在三维空间中,通过媒介的相互作用(即长程作用),只有平方反比作用一种,它的形式是由空间的维数决定的,而“旋”就是该作用下自然形成的一种“有核绕转”结构。而一切直接接触的相互作用(短程作用),都可以看成是“旋”的化合与分解。
旋与质点 “旋”,作为一个概念,表示普遍存在的粒子的“有核绕转”结构。“旋”不同于牛顿的质点模型,因为质点模型只是一个没有任何内部结构的几何点,它唯一的属性就是一个人为设定的质量。而“旋”有着递归的、无限可分的“有核绕转”结构。质点可以看作“旋”的远距离近似,因为当从远处观察时,“旋”的丰富的内部结构,由于距离远的缘故,是看不见的。然而,当从近处观察时,“旋”的结构的细节就不可忽视了。相比粒子的质点模型而言,粒子的“旋”模型具有某种优势,因为它避免了质点模型中来自粒子的“几何点表示”的零体积所带来的奇异性(奇点),但“旋”仍可以被看作一个点,当所关心的尺度远大于“旋”的直径的时候。
(2005年9月30日)
三、人工宇宙
(从人到神的跃变)
据《旧约》记载,造物主创造我们这个世界用了六天的时间。他先后创造了光、空气、植物等物。然而,圣经并未告诉我们造物主是从哪里来的,也未告诉我们创造过程的细节。在本节,我们将根据超广义相对论所提供的关于自然的新图景,给出关于创造过程的一些线索。这里我们将扮演“上帝”的角色,创造各种各样的虚拟世界。事实上,每个人都可以成为“上帝”,创造一个世界也不是很难:我们所需要的仅仅是一部自动机和一些程序设计的技巧。让我们从运行我们这个世界的那个模拟器的结构说起吧。
微观尺度:扩展的元胞自动机
元胞自动机与格子宇宙 关于元胞自动机的一个介绍性的定义,见参考文献20。这里元胞自动机被定义成一个八元组:
[math]\displaystyle{
CA=\{S,P,Q,C,I,D,N,U\}
}[/math] (53)
其中,S是一个空间,P是空间S的某种划分,S和P合称元胞空间;S的每一部分(即P的一个元素)称为一个元胞;Q是元胞状态的集合;C是元胞空间的边界条件;I是元胞空间的初始配置(构象);D是空间此刻的配置,即,在时步n,元胞状态在元胞空间中的分布;N是邻居规则;U是更新规则。
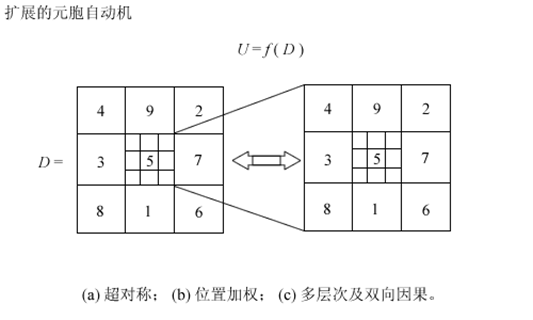
元胞自动机的扩展 为了创造一个栩栩如生的世界,我们从三个方面对上述的普通元胞自动机进行扩展:超对称、位置加权和多层次及双向因果(图 12)。因此,一个扩展的元胞自动机被定义成一个九元组:
[math]\displaystyle{
ECA=\{S,P,Q,C,I,D_l,N_F,U, R(D,U)\}
}[/math] (54)
其中,[math]\displaystyle{ D_l }[/math]是格子宇宙在观察尺度l所呈现的构象,[math]\displaystyle{ N_F }[/math]是位置加权的邻居规则,而[math]\displaystyle{ R(D,U) }[/math]是构象D和更新规则U之间的一个关系(超对称关系)。
图 12 扩展元胞自动机的示意图
(a)超对称:状态与规则之间的对称。在超空间中,状态和规则可以统一起来,即,它们可以存在于同一个存在水平并相互作用。
(b)位置加权:不同的位置被赋予不同的权重用来限定邻居对当前元胞的影响能力。这一做法可以增加或降低系统的对称程度,以使方形配置具有圆形配置的对称性,或者反之亦然。
(c)多层次及双向因果:元胞空间的自相似性在多层次上的体现。双向因果不同于还原主义之处在于,不仅底层的微观状态可以决定表层的宏观状态,而且表层的宏观状态可以反过来作用于底层的微观状态。双向因果使宏观状态从纯粹被动的模式变成一个可以主动起作用的模式。
光速与狭义相对论 在元胞自动机的游戏中,对于一个有限的物体而言,如果它每一时步移动一个元胞的距离,那么该物体具有最大的速度。已经证明,在元胞空间中,没有东西可以比此速度更快。因此,这一速度被称作光速。这一速度最大且不变的性质是狭义相对论的基础16。
宏观层次:模拟动力学
相应于超宇宙递归模拟的结构,模拟动力学是以迭代的方式对物理现象的模拟,它是人工宇宙的动力学。在模拟动力学中,系统的演化是一个过程,而一个系统的结构是该迭代过程的一个作为结果出现的吸引子。
相互作用与变换
现在考虑真实世界R中的物体A与虚拟世界V中的物体C’之间的相互作用。如我们目前所知,这两个物体之间的唯一的关联就是超变换,即,如果它们之间存在相互作用的话,那么,该作用必然要被表示成某种变换。事实上,作用的效果就是导致粒子/物体的运动或者是运动状态的改变,而这一效果可以被某一变换完成就像在计算机图形学中所作的那样21。因此,一个“相互作用”等价于一个“变换”。
惯性的起源
相互作用在亚里士多德的时代,被称作“力”,并被认为是运动的原因。伽利略可能是首先注意到物体惯性的人22,而笛卡尔指出物体的运动不需要一个持续的“推力”23。后来,伟大的物理学家,埃萨克·牛顿,给出了运动的三定律,并在他的第一定律中,澄清了“力”不是物体运动的原因,而是物体运动状态发生改变的原因24。换言之,如果没有这样的“原因”,物体将由于惯性而保持它的运动状态。
至于惯性的起源,迄今仍是一个谜。通过著名的水桶试验25,牛顿试图证明水的绝对运动(后来,他实验中所观察到的离心力被认为是“惯性力”)。但是,马赫不同意牛顿的观点,认为一个物体的惯性是宇宙中其他物体对该物体作用的结果26。现在,我们给出惯性起源的一个新解释,即惯性起源于“本模拟器”作为一个自动机的运行,即“本模拟器”的自动性就是惯性的起源。
模拟表示
现在考虑一个物理世界的模拟。我们所遇到的第一个问题就是如何表示被模拟世界中的粒子。一个自然的想法便是把粒子表示成被模拟空间中的一个点。但如果这样,我们将无处放置粒子的物理属性,因为一个点只有一个属性,即它在被模拟空间中的位置。当然,我们在编程时,可以人为地设置某些物理属性,即,我们定义一个变量并赋一个物理量给它,然后,将这个变量和一个几何点关联起来。但是这一做法将导致另一缺陷——奇点——,像牛顿的质点模型那样。在牛顿的质点模型中,因为一个点的体积为零,任何有限的质量赋予它之后,都会导致无穷大的密度,即奇异性。
考虑到上述缺陷,我们把一个粒子表示成被模拟空间中的一个点集。粒子/物体的“点集表示”统一了核与场的图像。粒子表示成一个点集,而场则表示成在某一变换下的点的“部分流”。而粒子/物体的运动则表示成在另一变换下的点集整体的流动。部分变换造成了点集的一部分的快速的流动,而全局变换则使得整个点集发生相对慢速的流动。
点集中的每一个点,如果在更精微的尺度观察,仍是一个点集。即,点集具有自相似性。两种类型的电荷表示成“点流”的两个方向:向心与离心。参照分形几何理论27,粒子可以被表示成被模拟空间中的一个波雷尔集,而物体,作为粒子的集合,可以被表示成粒子点集的并集。如此一来,物理属性可以表示成点集上的某种测度。通过定义不同的测度,不同的物理量就可以被模拟出来。
粒子/物体的运动被表示成作用在它上面的变换就像在计算机图形学中所做的那样21。粒子/物体间的关系被表示成分形空间(F(S),h(d))中两个点集之间的豪斯道夫距离,分形空间(F(S),h(d))定义在距离空间(S,d)上。在模拟动力学中,时间维被模拟器的运行所占据,故此,在动力学方程中,只有空间变量是显式的,而时间是隐式的,作为下角标出现。
迭代公式
单个粒子/物体 设粒子/物体由被模拟空间S中的点集P(波雷尔集)表示,则它的运动方程为:
[math]\displaystyle{
P_{n+1}=\hat{T}(\mu(P,q))\cdot{P_n}, n=0,1,2,\dots
}[/math] (55)
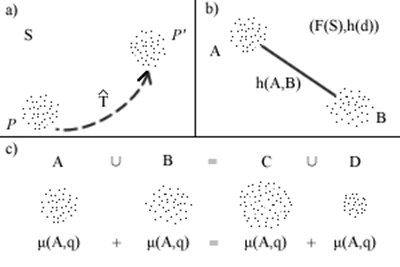
其中,[math]\displaystyle{ P_n }[/math]是粒子/物体P在迭代过程中的时步n的状态,而[math]\displaystyle{ P_{n+1} }[/math]是P在时步n+1的状态;[math]\displaystyle{ \hat{T} }[/math]是作用在[math]\displaystyle{ P_n }[/math]上的一个变换,它是变量[math]\displaystyle{ \mu(P,q) }[/math]的函数,而[math]\displaystyle{ \mu(P,q) }[/math]是点集P的q维豪斯道夫测度;“[math]\displaystyle{ \cdot }[/math]”表示[math]\displaystyle{ \hat{T} }[/math]变换作用于点集P上。粒子运动的一个例子见图13 a)。
两个粒子/物体 设两个粒子/物体被分别表示成被模拟空间中的两个点集A和B(波雷尔集),则它们的动力学方程为:
[math]\displaystyle{
(A\cup{B})_{n+1}=\hat{T}(\mu(A,q),\mu(B,q),h(A,B))\cdot(A\cup{B})_n, n=0,1,2,\dots
}[/math] (56)
其中,[math]\displaystyle{ (A\cup{B})_n }[/math]是两个粒子/物体A和B在迭代过程中的时步n的状态(位置),而[math]\displaystyle{ (A\cup{B})_{n+1} }[/math]则是A和B在时步n+1的状态;[math]\displaystyle{ \hat{T} }[/math]是作用在[math]\displaystyle{ (A\cup{B})_n }[/math]上的变换,它是变量[math]\displaystyle{ \mu(A,q) }[/math]、[math]\displaystyle{ \mu(B,q) }[/math]和[math]\displaystyle{ h(A,B) }[/math]的函数,而[math]\displaystyle{ \mu(A,q) }[/math]和[math]\displaystyle{ \mu(B,q) }[/math]是点集A和B的q维豪斯道夫测度,[math]\displaystyle{ h(A,B) }[/math]则是A和B之间定义在分形空间[math]\displaystyle{ (F(S),h(d)) }[/math]上的豪斯道夫距离,而[math]\displaystyle{ (F(S),h(d)) }[/math]中的d则是定义在被模拟空间S上的距离;“[math]\displaystyle{ \cdot }[/math]”表示变换[math]\displaystyle{ \hat{T} }[/math]作用在点集A和B的并集上。粒子间豪斯道夫距离的一个例子见图13 b)。
多粒子/物体 设这些粒子/物体分别由[math]\displaystyle{ A_1,A_2,\dots,A_N }[/math]表示,则它们的动力学方程是:
[math]\displaystyle{
(A_1\cup\dots\cup{A_N})_{n+1}=\hat{T}(\mu(A_1,q),\dots,\mu(A_N,q),h_k(A_i,A_j),k=1,\dots,C_N^2)\cdot(A_1\cup\dots\cup{A_N})_n
}[/math] (57)
其中,[math]\displaystyle{ (A_1\cup\dots\cup{A_N})_n }[/math]是这些粒子/物体在迭代过程中时步n的状态(位置),而[math]\displaystyle{ (A_1\cup\dots\cup{A_N})_{n+1} }[/math]是这些物体在时步n+1的状态;[math]\displaystyle{ \hat{T} }[/math]是作用在[math]\displaystyle{ (A_1\cup\dots\cup{A_N})_n }[/math]上的变换,它是变量[math]\displaystyle{ \mu(A_1,q) }[/math]、…、[math]\displaystyle{ \mu(A_N,q) }[/math]和[math]\displaystyle{ h_k(A_i,A_j) }[/math]的函数,而[math]\displaystyle{ \mu(A_1,q) }[/math]…、[math]\displaystyle{ \mu(A_N,q) }[/math]是点集[math]\displaystyle{ A_1,A_2,\dots,A_N }[/math]的q维豪斯道夫测度,[math]\displaystyle{ h_k(A_i,A_j) }[/math],[math]\displaystyle{ k=1,\dots,C_N^2 }[/math]则是这些物体间定义在分形空间[math]\displaystyle{ (F(S),h(d)) }[/math]上的豪斯道夫距离,而[math]\displaystyle{ (F(S),h(d)) }[/math]中的d则是定义在被模拟空间S上的距离;“[math]\displaystyle{ \cdot }[/math]”表示变换[math]\displaystyle{ \hat{T} }[/math]作用在点集[math]\displaystyle{ A_1,A_2,\dots,A_N }[/math]的并集上。
对于多体问题,为了避免距离数目的组合爆炸以便更有效地进行计算,我们可以定义整个系统的一个合适的全局测度,如此一来,动力学方程可被写作:
[math]\displaystyle{
(A_1\cup\dots\cup{A_N})_{n+1}=\hat{T}(\mu_r(A_1\cup\dots,{A_N},q_r))\cdot(A_1\cup\dots\cup{A_N})_n
}[/math] (58)
其中,[math]\displaystyle{ \mu_r(A_1\cup\dots,{A_N},q_r) }[/math]是整个系统[math]\displaystyle{ A_1\cup\dots\cup{A_N} }[/math]的维豪斯道夫测度。
方程(55)、(56)、(57)和(58)分别是单体、两体和多体的模拟动力学的动力学方程。
碰撞:测度守恒律
粒子A占据空间的一部分,粒子B也一样。当它们相遇时,代表它们的点集在某种程度上彼此重合在一起。结果便是它们湮灭了,它们的并集作为一个新粒子生成,同时,它们的交集作为另一个新粒子被释放出来(图 13 c))。在这一过程中,点集的总大小守恒,从而导致了豪斯道夫测度的守恒。因为物理量被表示成了某种豪斯道夫测度,它们在这一过程中也守恒。因此,物理世界的守恒律就被模拟出来了。当一组粒子聚集形成一个物体时,这个物体就是代表这些粒子的点集的并集,而这些点集的交集被释放出来,而被释放出来的点集上的某种测度可以被称为(如我们这个世界中那样):结合能。
图 13 空间S中模拟动力学的图示。a) 粒子P在变换T的作用下从空间S中的位置P移动到P’处;b) h(A,B)表示粒子A与粒子B在分形空间(F(S),h(d))中的豪斯道夫距离;c) 粒子A与粒子B碰撞,湮灭,粒子C与粒子D生成。原来被A和B所占据的一部分空间因为它们的重合而被释放出来。释放了的部分为D,即有,D=A∩B。相应地,q维豪斯道夫测度在这一过程中守恒。
三类结构
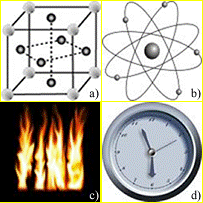
现在我们考虑被模拟世界中的系统结构。如我们在我们世界中所知道的那样,主要有三类结构:静态结构、周期运动结构和耗散结构。它们可以分别由迭代过程(动态系统)的三类吸引子来模拟。如图14所示,静态结构(图14 a)),如晶体,可由不动点吸引子模拟;周期运动结构(图14 b)),如原子,可由极限环吸引子模拟;而耗散结构(图14 c)),如火焰,可由混沌吸引子模拟。当然,还存在这些基本结构的混合结构,如钟表(图14 d))(静态结构与周期运动结构的混合结构),被模拟世界中的人们可以用这样的混合结构来计时,如我们在我们这个世界中所做的那样:看表计时。
图 14 模拟动力学中的系统结构。a) 静态结构,由不动点吸引子模拟;b) 周期运动结构,由极限环吸引子模拟;c) 耗散结构,由混沌吸引子模拟;d) 静态与周期运动结构的混合结构,可以用作计时器。
人工实在的层次与演化
人工宇宙:自存在系统,人工实在的物理基础。人工宇宙是该宇宙“超在物”的作品。
人工生命:自生产系统,可与环境发生相互作用的主动个体。人工生命是人工宇宙的演化结果。
人工智能:自反映系统。自反映是某种形成第二实在(主观世界)的能力,相对于该系统所在的第一实在(物质世界)而言。对于一个生物体而言,要具有智能,如下三点是必不可少的:(1)同时拥有第一实在(躯体世界)和第二实在(思想世界);(2)生活在这两个实在的叠加态中;(3)具有超变换的能力,即在这两个世界间跳跃的能力。人工智能是人工生命进化的结果。
人工社会:智能主体的自组织系统。智能主体间的相互依赖关系使它成为一个“类生系统”。人工社会是人工宇宙演化的结果。
科学与宗教的统一
- 科学与宗教 超广义相对论有望统一科学与宗教。 造物主是模拟器的制造者。对于我们所居住的这个“神”造的世界来说,我们是被创造出来的生灵,而对于生活在人造的虚拟世界中的生灵来说,我们就是他们的造物主。未来将是一个“神”(我们的造物主)、人(我们)和人工人(我们的创造物,包括机器人和虚拟生灵)杂居的时代。
- 宇宙和生命的起源 本文中共提到了三类模拟器:“本模拟器”、人脑和计算机。“本模拟器”即是我们这个世界运行于其上的那个模拟器,它是个“神”造的模拟器;人脑是我们这个世界中的物质长期演化的结果;而电脑则是人造的模拟器。这三类模拟器分别模拟了三类世界:客观物质世界、主观精神世界和计算机虚拟世界。同时考虑这三类世界以及生活在它们中的生灵,我们就会认识到,宇宙和生命的起源,既不是一个简单的创造,也不是一个简单的进化,而是它们的某种混合。因此,超广义相对论统一了“创世说”与“进化论”。(统一之后的观点可以称为:“创进论”)
- 造物主的非全知全能性 造物主是模拟器的制造者。因为模拟器是一个自动机,它的制造者可以通过设定一些简单的规则来创造一个世界,然而却不能完全地知道和决定模拟器的运行结果,这正是由于自动机的自动性。但是造物主有能力打破他所制定的规律,而直接对他所创造的世界施加影响,造成改变,而这种现象的出现,从被创造物的角度看,就称之为“神迹”。造物主作为他所创造的世界的“超在物”,当他位于“超存在”的位置时,相对于它的创造物而言,有着更强大的能力。然而,当他进入他所创造的世界时,为了存在,它也必须遵守它自己制定的游戏规则。因此,造物主和被创造物是相对的,它们作为存在物是平权的。
四、讨论与结论
讨论
- 真实性的量化 既然真实性不是绝对的而是相对的,事件的真实性在某种程度上就是可比较的,这将导致真实性的量化。
- 物理与数学 微积分的发明支持了经典力学的建立,而复分析的发展支持了量子力学的建立。现在,非线性科学的出现,特别是分形几何与动态系统理论的出现,将支持模拟动力学的建立。 经典力学的公式形式是实微分方程,量子力学的公式形式是复的偏微分方程,而模拟动力学的公式形式是迭代方程。模拟动力学的公式形式,与经典和量子力学的显著不同之处在于,它的动力学方程中没有时间变量。
- 两个视角:“在”与“外” 在超宇宙的图景中,物理研究有两个视角:“在”与“外”。“在”的视角即是被模拟世界中的视角,而“外”的视角即是模拟世界中的视角。在相似力学中,两个视角是“微观”与“宏观”;在运动相对论中,两个视角即“运动者一方”和“旁观者一方”。模拟动力学的动力学方程是在“外”的视角建立的。当视角从“外”转到“在”的时候,它或许可以退化到经典力学或量子力学的形式。从今以后,物理学研究,特别是基础物理的研究,有了一个可供选择的建立物理方程的视角。从“在”视角上看,力学是相对的,而从“外”视角上看,力学是绝对的。
- 超物理学。超物理学是物理学、元物理学和哲学的统一。超物理学主要包括两个分支:超宇宙学和心物理学。超宇宙学是虚拟现实概念的发展,旨在给出递归虚拟世界的一个统一的描述。心物理学是心灵学的重定义,旨在给出物质世界和精神世界的一个统一的描述。
- 悖论与存在 悖论不等于不存在。悖论通常发生在自反映的情形中,比如罗素的集合学悖论。悖论仅存在于“在”视角,而对于一个站在“外”视角上的旁观者来说,很多悖论根本就不存在。
- 为何存在? “存在”对每个人而言,都只是一个简单的事实。我们没有选择是否出生以及生于何时何地的权利。所以绝大部分人都接受“存在”这一事实。然而,总有一些人喜欢问为什么。这些人通常是理性主义者而相信逻辑。这里有一个答案给他们。试着回答下面这个问题: “不存在”存在吗?如果“不存在”存在,那么,它便不是不存在,即,结果是只有存在;如果“不存在”不存在,那么,结果也是只有存在。故此,“存在”是逻辑的必然结果。
结论
真实性是相对的;真实性不等于物理定律。宇宙可能具有多个存在水平。超宇宙作为一个虚拟世界网,是一个大分形。我们的世界可能运行在一个模拟器上。模拟是宇宙建模的一种方法论。“超变换”桥接了三个世界:客观物质世界、主观精神世界和计算机虚拟世界,这使我们有可能给出自然的一个统一的描述。我们的世界是一个由递归的“有核绕转” 结构(“旋”)组成的大分形。我们这个世界基本作用的形式是由空间的维数决定的。我们这个世界中唯一的长程相互作用是平方反比作用,而一切短程相互作用都可以看成是不同存在层次上的“旋”的化合与分解。人工宇宙的创建要采取微观与宏观相结合的手段:在微观水平上可以采取扩展的元胞自动机的形式,而在宏观水平上,可以采取模拟动力学的形式。物理研究存在两个视角:“在”与“外”。在超广义相对论中,两个视角分别为:“被模拟世界”与“模拟世界”;在狭义超广义相对论中,两个视角分别为:“微观水平”与“宏观水平”;而在狭义相对论中,两个视角分别为:“运动者一方”与“旁观者一方”。两个视角的存在是真实性的相对性的反映。
(2005年12月30日)
参考文献
- http://www.thematrix.com
- A. Einstein, Ann. Phys. 17, 891 (1905).
- The complete works of Chuang Tzu, translated by Burton Watson, Columbia University Press, New York, (1968). Or see the translation by Lin Yutang at this website http://www.clas.ufl.edu/users/gthursby/taoism/cz-text2.htm
- 郭硕鸿,《电动力学》, 第二版,高等教育出版社,北京,1997.
- David Griffith, “Introduction to Elementary Particles”, John Wiley, New York, 1987.
- Stephen Hawking, “A Brief History of Time”, Bantam Books, New York, 1988
- Stephen Hawking, “The universe in a nutshell”, Bantam Books, New York, 2001.
- Brian R. Greene, “The Elegant Universe”, Brockman Vintage Press, 1999.
- W. Heisenberg, “Die Physikalischen Prinzipien der Quantent theorie”, 4 Auflage, Verlag von S. Hirzel, 1944.
- 曾谨言,《量子力学》,第三版,科学出版社,北京,2000.
- L. De Broglie, The Beginnings of Wave Mechanics, (in “Wave Mechanics, the first fifty years”, 1973, editted by W. C. Price), University of London King’s College, Butterworth & Co.
- G. J. Davisson, L. H. Germer, Phys. Rev., 30, 705, (1927)
- S. Schrödinger, Ann. D. Phys., 4, 1926.
- M. Born, Zeit. Physik, 38 (1926) p. 803.
- I. Prigogine, “The End of Certainty”, The Free Press, New York, 1997.
- A. Einstein, H. A. Lorentz, H. Minkowski, H. weyl, “The Principle of Relativity”, Dover, 1923
- A. Einstein, “The Meaning of Relativity”, 5th Ed., MJF Books, New York, 1997.
- http:// www.arxiv.org/physics/0505194.
- P. C. W. Davies, J. R. Brown, “Superstrings: a theory of everything?”, Cambridge University Press, 1988., Contributors: Oscar Klein; John Schwarz & Michael Green; Edward Witten & John Ellis & Abdus Salam & Steven Weinberg; David Gross; Sheldon Glashow & Richard Feynman.
- B. Chopard, M. Droz, “Cellular Automaton Modeling of Physical Systems, Cambridge University Press, Cambridge, 1998
- Donald Hearn and M. Pauline Baker, “Computer Graphics with OpenGL” 3rd Ed., Pearson Prentice Hall, USA , 2004.
- Galileo, “Dialogues Concerning Two New Sciences”, (1638) or “Two New Sciences”, MacMillan, 1914.
- R. Dugas, “A History of Mechanics”, Routledge & Kegan Paul, 1955.
- I. Newton, “Mathematical Principles of Natural Philosophy”, University of California Press, 1946.
- I. Newton, Mathematical Principles of Natural Philosophy, University of California Press, 1946 (p.10).
- E. Mach, The Science of Methanics, Open Court, 1919, pp.223-224
- K. J., Falconer, “Fractal Geometry: Mathematical Foundation and Applications”, Wiley, New York, 1990.