负熵
在信息论和统计学中,负熵( negentropy)被用于度量与正态分布之间的距离。“负熵 negative entropy”这一概念是埃尔温·薛定谔 Erwin Schrödinger在他1944年的科普著作《生命是什么? What is Life?》中首次提出,[1]后来莱昂·布里渊 Léon Brillouin把这个短语缩写为“负熵 negentropy”。[2][3]1974年,阿尔伯特·圣捷尔吉 Albert Szent-Györgyi提出用“syntropy”(这个可能源于20世纪40年代意大利数学家Luigi fantappi的术语)来代替“negentropy”以建立一个生物学和物理学的统一理论。虽然巴克敏斯特·福乐 Buckminster Fuller试图推广这一思想,但是迄今为止负熵仍更为人们广泛使用。
在《生命是什么? What is Life?》的一项注释中,Schrödinger解释了他使用这个短语的原因,如下:
... if I had been catering for them [physicists] alone I should have let the discussion turn on free energy instead. It is the more familiar notion in this context. But this highly technical term seemed linguistically too near to energy for making the average reader alive to the contrast between the two things.如果我只为了迎合物理学家们,那么我就会让讨论转向热力学自由能 free energy。在这个语境中,自由能是物理学更熟悉的概念。但是,这个高度专业的术语在语言学上似乎太接近于能量 energy,以至于普通读者无法生动地看到两者之间的区别。
2009年,Mahulikar 和 Herwig 将动态有序子系统的负熵重新定义为有序子系统相对于周围混沌的特定熵赤字。[4]因此,根据单位质量的熵定义负熵的 SI 单位为(J kg−1 K−1) ,其中(K−1)的定义基于单位能量的熵。这个定义表明: 1)动态有序存在的尺度不变的热力学表示,2)动态有序存在和演化的专门物理原理,3)Schrödinger关于负熵的数学解释。
信息论 Information theory
在信息论和统计学中,负熵可用来度量某个分布到正态分布的距离。[5][6][7] 在所有具有给定均值和方差的分布中,正态分布或高斯分布的熵最大。负熵也用来度量具有与它相同均值和方差的给定分布和正态分布之间熵的差距。因此,负熵总是非负的,在任何线性可逆的坐标变换下都是不变的,当且仅当分布表现为高斯分布 Gaussian distribution时才变为零。
负熵定义为:
- [math]\displaystyle{ J(p_x) = S(\varphi_x) - S(p_x)\, }[/math]
其中,[math]\displaystyle{ S(\varphi_x) }[/math]表示与[math]\displaystyle{ p_x }[/math]具有相同均值和方差的高斯密度的微分熵,[math]\displaystyle{ S(p_x) }[/math]表示[math]\displaystyle{ p_x }[/math]的微分熵:
- [math]\displaystyle{ S(p_x) = - \int p_x(u) \log p_x(u) \, du }[/math]
负熵通常用于统计和信号处理。它与网络熵有关,网络熵常用于独立成分分析 independent component analysis。[8][9]
一个分布的负熵等于 [math]\displaystyle{ p_x }[/math] 和具有与 [math]\displaystyle{ p_x }[/math] 相同均值和方差的正态分布的 Kullback-Leibler 散度(参见正态分布的微分熵 Differential entropy和最大化)。特别地,负熵总是非负的。
统计学负熵与吉布斯自由能的关联 Correlation between statistical negentropy and Gibbs' free energy
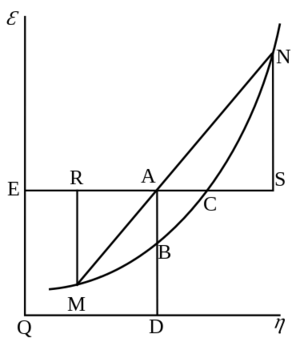
存在一个与自由能(自由焓 free enthalpy)密切相关的物理量,它具有熵的单位并且与我们所知的统计学和信息论中的负熵同构。1873年,约西亚·威拉德·吉布斯 Josiah Willard Gibbs创建了一个图表,说明了自由能对应于自由焓的概念。在图表上,我们可以看到称为熵的容量 capacity for entropy的物理量。这个量表示在不改变内能 internal energy体积的情况下可增加的熵值。[10] 换句话说,它是在假定条件下可能的最大熵与实际熵之间的差异。它恰好符合统计学和信息论中负熵的定义。1869年,Massieu 在等温过程 isothermal process[11][12][13](两个量只有一个图形符号不同)中引入了一个类似的物理量,[14]后来 Planck 把这个概念引入到等温-等压 isothermal-isobaric process过程中。近期,Massieu–Planck 提出的热力学势,也被称为自由熵,[15]已被证明在所谓的统计力学熵表述中发挥了重要作用,应用于分子生物学[16] 和热力学非平衡过程。[17]
- [math]\displaystyle{ J = S_\max - S = -\Phi = -k \ln Z\ }[/math]
- 其中:
- [math]\displaystyle{ S }[/math] 代表熵
- [math]\displaystyle{ J }[/math] 代表负熵(吉布斯“熵的容量”)
- [math]\displaystyle{ \Phi }[/math] 代表 Massieu 势
- [math]\displaystyle{ Z }[/math] 代表配分函数
- [math]\displaystyle{ k }[/math] 代表波兹曼常数 Boltzmann constant
特别地,数学上的负熵(负熵函数,在物理学中解释为自由熵)是 LogSumExp 的凸共轭(在物理学中解释为自由能)。
布里渊信息负熵原理 Brillouin's negentropy principle of information
1953年,Léon Brillouin推导出一个一般性方程,证明了改变一个信息的比特值至少需要 kT ln (2)的能量。这与理想情况下 Leó Szilárd 的引擎所产生的能量相等。在他的书中,[18]他进一步探讨了这个问题并得出结论: 任何条件下一个比特的改变(测量、关于是/否问题的决定、擦除、显示等等)都需要消耗同等的能量。
参见
注释
- ↑ Schrödinger, Erwin, What is Life – the Physical Aspect of the Living Cell, Cambridge University Press, 1944
- ↑ Brillouin, Leon: (1953) "Negentropy Principle of Information", J. of Applied Physics, v. 24(9), pp. 1152–1163
- ↑ Léon Brillouin, La science et la théorie de l'information, Masson, 1959
- ↑ Mahulikar, S.P. & Herwig, H.: (2009) "Exact thermodynamic principles for dynamic order existence and evolution in chaos", Chaos, Solitons & Fractals, v. 41(4), pp. 1939–1948
- ↑ Aapo Hyvärinen, Survey on Independent Component Analysis, node32: Negentropy, Helsinki University of Technology Laboratory of Computer and Information Science
- ↑ Aapo Hyvärinen and Erkki Oja, Independent Component Analysis: A Tutorial, node14: Negentropy, Helsinki University of Technology Laboratory of Computer and Information Science
- ↑ Ruye Wang, Independent Component Analysis, node4: Measures of Non-Gaussianity
- ↑ P. Comon, Independent Component Analysis – a new concept?, Signal Processing, 36 287–314, 1994.
- ↑ Didier G. Leibovici and Christian Beckmann, An introduction to Multiway Methods for Multi-Subject fMRI experiment, FMRIB Technical Report 2001, Oxford Centre for Functional Magnetic Resonance Imaging of the Brain (FMRIB), Department of Clinical Neurology, University of Oxford, John Radcliffe Hospital, Headley Way, Headington, Oxford, UK.
- ↑ Willard Gibbs, A Method of Geometrical Representation of the Thermodynamic Properties of Substances by Means of Surfaces, Transactions of the Connecticut Academy, 382–404 (1873)
- ↑ Massieu, M. F. (1869a). Sur les fonctions caractéristiques des divers fluides. C. R. Acad. Sci. LXIX:858–862.
- ↑ Massieu, M. F. (1869b). Addition au precedent memoire sur les fonctions caractéristiques. C. R. Acad. Sci. LXIX:1057–1061.
- ↑ Massieu, M. F. (1869), Compt. Rend. 69 (858): 1057.
- ↑ Planck, M. (1945). Treatise on Thermodynamics. Dover, New York.
- ↑ Antoni Planes, Eduard Vives, Entropic Formulation of Statistical Mechanics, Entropic variables and Massieu–Planck functions 2000-10-24 Universitat de Barcelona
- ↑ John A. Scheilman, Temperature, Stability, and the Hydrophobic Interaction, Biophysical Journal 73 (December 1997), 2960–2964, Institute of Molecular Biology, University of Oregon, Eugene, Oregon 97403 USA
- ↑ Z. Hens and X. de Hemptinne, Non-equilibrium Thermodynamics approach to Transport Processes in Gas Mixtures, Department of Chemistry, Catholic University of Leuven, Celestijnenlaan 200 F, B-3001 Heverlee, Belgium
- ↑ Leon Brillouin, Science and Information theory, Dover, 1956
本中文词条由Jxzhou翻译,CecileLi审校,舒寒、薄荷编辑,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。