阈值模型
此词条暂由Potatozh初译,未经审校,带来阅读不便,请见谅。
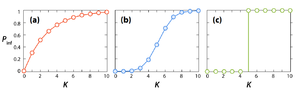
For disease epidemics it is customary to assume that a susceptible individual has a constant probability to receive the infection from a peer upon every exposure, independently of whether other infected individuals are simultaneously in contact or other exposures have occurred in the past. While generally reasonable for the transmission of pathogens [although exceptions may occur [1] ], this hypothesis is clearly unrealistic in most situations where a social meme is spreading: a piece of information is more credible if arriving from different sources; the push to adopt a technological innovation is stronger if neighboring nodes in the social network have already adopted it. These considerations lead naturally to the introduction of “threshold models” for spreading phenomena, where the effect of multiple exposures changes from low to high as a function of their number. Figure 14 displays the probability of infection (adoption) Pinf after K attempts in the different scenarios. In the case of SIR each attempt has a fixed probability $p$ of success and $P_{inf}=1-(1-p)^K$.
疾病传播过程中,习惯上假定易感个体在每次接触已感染个体时以常数概率被感染,而与过去是否同时接触其他感染个体或发生其他接触暴露无关。 上述假定通常对于疾病传播是合理的(尽管可能会发生例外情况),但是在含有社会模因传播的多数情况下,这种假设显然是不真实的:在信息传播过程中,往往多渠道传播过来的信息会相对更加可靠;在某项技术创新的传播中,如果社会网络中某个节点的多个周围邻居已经接受该技术创新,则此节点接受该技术创新的动力会更强。综合以上考虑,则就很自然地会导致在针对信息扩散现象引入“阈值模型”,其中多次暴露的影响随其数量的增加从低到高变化。左图显示了感染(接受信息)的可能性$P_{inf}$在不同情况下进行$K$尝试后的结果。对于SIR(图(a)),每次尝试都有固定的成功概率$p$和$P_{inf}=1-(1-p)^K$。
Watts阈值模型
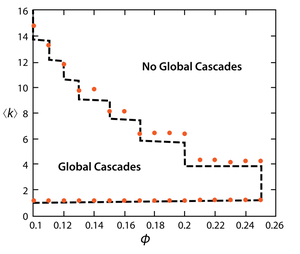
Threshold models have a long tradition in the social and economical sciences [2] [3]. In the context of spreading phenomena on complex networks, a seminal role has been played by the model introduced by Watts (2002)[4]. Each individual can be in one of two states (S and I) and is endowed with a quenched, randomly chosen threshold value $\Phi_i$. In an elementary step an individual agent in state S observes the current state of its neighbors and adopts state I if at least a threshold fraction $\Phi_i$ of its neighbors is in state I; else it remains in state S.No transition from I back to S is possible. Initially all nodes except for a small fraction are in state S. Out of these initiators a cascade of transitions to the I state is generated. The nontrivial question concerns whether the cascade remains local, i.e., restricted to a finite number of individuals, or it involves a finite fraction of the whole population. Given an initial seed, the spreading can occur only if at least one of its neighbors has a threshold such that $\Phi_i\leq1/k_i$. A cascade is possible only if a cluster of these “vulnerable” vertices is connected to the initiator. For global cascades to be possible it is then conjectured that the subnetwork of vulnerable vertices must percolate throughout the network. The condition for global cascades can then be derived applying on locally treelike networks the machinery of generating functions for branching processes. In the simple case of a uniform threshold $\Phi$ and an Erdős-Rényi pattern of interactions the phase diagram as a function of the threshold $\Phi$ and of the average degree $\left<k\right>$ is reported in Fig. 15. For fixed $\Phi$, global cascades occur only for intermediate values of the mean connectivity $1<\left<k\right><1/\Phi$. The transition occurring for small $\left<k\right>$ is trivial and is not due to the spreading dynamics: the average cascade size is finite for $\left<k\right><1$ because the network itself is composed of small disconnected components: the transition is percolative with power-law distributed cascade size. For large $\left<k\right>>1/\Phi$ instead, the propagation is limited by the local stability of nodes.
阈值模型在社会和经济科学中具有悠久的传统(Granovetter,1978;Morris,2000)。在复杂网络上传播现象的背景下,Watts(2002)引入的Watts阈值模型发挥了开创性的作用。 每个人都可以处于两种状态之一,即易感态和感染态(S和I),并具有随机分配的“阈值”$\Phi_i$。在模型的基本步骤中,处于状态S的个体观察其邻居的当前状态来决定自己采用的状态,如果其邻居中有至少$\Phi_i$比例的个体处于状态I,则其决定采用的状态为I;否则仍保持为S状态。网络中状态为S的个体一旦转变为I态,则不再能转换回到S状态。在传播初始阶段,随机选择很少部分的节点处于I状态,作为种子节点,其余节点都处于S状态。这些种子节点会产生级联过程,使网络中节点由S状态转变为I状态。一个非平庸的问题是这样的级联过程是否是仅限于局域上有限数量的个体转变为I状态,还是全局范围有限部分的个体转变为I状态。对于初始种子只有一个的情况下,仅当其邻居中的至少一个个体的采纳阈值为$\Phi_i\leq1/k_i$时,才可能发生信息传播,而这样的邻居可以称为易受攻击(vulnerable)的节点。只有将这些“易受攻击的”节点簇(cluster)连接到种子节点时,级联才可能发生。而如果想使全局级联成为可能,则很自然地可以推测这些易受攻击节点的子网络必须遍及整个网络。全局级联的条件可以通过在局部树状网络上使用分支过程的生成函数理论来推导得出。当假设每个节点的阈值$\Phi_i$为相同的常数值$\Phi$时,左图中显示了ER网络上以阈值$\Phi$和平均度$k$为参数空间的信息传播范围的相图。对于固定的$\Phi$,全局级联仅限于当平均度$\left<k\right>$满足$1<\left<k\right><1/\Phi$时才可能发生。平均度$\left<k\right>$很小时,没有产生全局范围级联的结果是平庸的,没有全局级联这是因为当平均度太小时,网络本身是由小的不连通的部分组成的。相反,对于较大的平均度$\left<k\right>>1/\Phi$,传播则是受节点的局部稳定性限制的。
参考文献 References
- ↑ Joh R I, Wang H, Weiss H, et al. Dynamics of indirectly transmitted infectious diseases with immunological threshold[J]. Bulletin of mathematical biology, 2009, 71(4): 845-862.
- ↑ Granovetter M. Threshold models of collective behavior[J]. American journal of sociology, 1978, 83(6): 1420-1443.
- ↑ Morris S. Contagion[J]. The Review of Economic Studies, 2000, 67(1): 57-78.
- ↑ Watts D J. A simple model of global cascades on random networks[J]. Proceedings of the National Academy of Sciences, 2002, 99(9): 5766-5771.
此页参考来源: Pastor-Satorras R, Castellano C, Van Mieghem P, et al. Epidemic processes in complex networks[J]. Reviews of modern physics, 2015, 87(3): 925.