路德维希·玻尔兹曼 Ludwig Edward Boltzmann
概述
路德维希·爱德华·玻尔兹曼(奥地利,1844年2月20日-1906年9月5日),物理学家、化学家和哲学家。他最伟大的功绩之一是发展了通过原子(当时甚至还不是一个公认的存在)的性质来解释和预测物质的物理性质的统计热力学,并且从统计概念出发,完美地阐释了热力学第二定律。
基本信息
| 类别 | 信息 |
|---|---|
| 姓名 | 路德维希·玻尔兹曼 Ludwig Edward Boltzmann |
| 出生日期 | 1844年2月20日 |
| 出生地 | 维也纳,奥地利帝国(1867年改组为奥匈帝国) |
| 去世日期 | 1906年9月5日 |
| 死亡地点 | 杜伊诺,的里雅斯特,奥匈帝国 |
| 死因 | 上吊自杀 |
| 国籍 | 奥地利 |
| 母校 | 维也纳大学 |
| 博士生导师 | 维也纳大学 |
| 母校 | Josef Stefan |
| 学术顾问 | Robert Bunsen,Leo Königsberger,Gustav Kirchhoff,Hermann von Helmholtz |
| 博士生 | Paul Ehrenfest,Philipp Frank,Gustav Herglotz,Franc Hočevar,Ignacij Klemenčič |
| 杰出学生 | Lise Meitner,Stefan Meyer |
| 成就 | 玻尔兹曼常数,玻尔兹曼方程,玻尔兹曼分布,细致平衡(精细平衡),H-定理,麦克斯韦-玻尔兹曼分布,斯特凡-玻尔兹曼常数,斯特凡-玻尔兹曼定律,麦克斯韦-玻尔兹曼统计,玻尔兹曼因子,认识论的理想主义 |
| 主要研究方向 | 物理学,哲学 |
| 所在机构 | 格拉茨大学,维也纳大学,慕尼黑大学,莱比锡大学 |
| 签名 |
路德维希·爱德华·玻尔兹曼 Ludwig Eduard Boltzmann(1844年2月20日—1906年9月5日),奥地利物理学家、哲学家。他最伟大的功绩是发展了统计力学,并且从统计意义出发解释了热力学第二定律。1877年,他给出了熵的定义,即玻尔兹曼熵公式:[math]\displaystyle{ S = k_{\rm B} \ln \Omega \! }[/math],将熵解释为系统统计无序性的度量。[1] 马克斯·普朗克 Max Planck命名kB为玻尔兹曼常数 Boltzmann constant。[2]
统计力学是现代物理学的支柱之一。它描述了宏观观察量(如温度和压力)如何与围绕平均值波动的微观参数相联系。它将热力学量(比如热容)与微观行为联系起来,而在经典热力学中,唯一可行的选择就是测量各种材料的热力学量,然后列成表格。[3]
个人简介
童年时光与教育经历
玻尔兹曼出生在维也纳郊区的埃尔德伯格。祖父是一名钟表制造商,从柏林搬到维也纳。父亲路德维希·格奥尔格·玻尔兹曼是一名税务官员,母亲卡塔琳娜·波恩芬德来自萨尔茨堡。他在家里接受了启蒙教育。[4]高中时光在上奥地利的林茨度过。玻尔兹曼15岁时,他的父亲去世了。[5]
从1863年开始,玻尔兹曼在维也纳大学学习数学和物理。他于1866年获得博士学位,1869年获得任教资格。波尔兹曼与物理研究所所长约瑟夫·斯特凡 Josef Stefan密切合作。正是斯特凡把玻尔兹曼引入了麦克斯韦的研究。[5]
学术生涯
1869年,25岁的玻尔兹曼经斯特凡的推荐,被任命为斯蒂里亚省格拉茨大学的数学物理正教授。[6]1869年,他在海德堡与罗伯特·本森 Robert Bunsen和里奥·柯尼斯堡 Leo Königsberger一起工作数月,1871年在柏林与古斯塔夫·基尔霍夫 Gustav Kirchhoff和赫尔曼·冯·赫姆霍尔兹 Hermann von Helmholtz进行合作。1873年玻尔兹曼加入维也纳大学担任数学教授,直至1876年。
1872年,远在女性可以被奥地利大学录取之前,他遇到了亨里埃特·冯·艾根特勒 Henriette von Aigentler,这是一位有抱负的格拉茨数学和物理女教师。然而她被拒绝旁听大学讲座。玻尔兹曼支持她上诉的决定,之后上诉成功。1876年7月17日,路德维希·玻尔兹曼与亨里埃特结婚;他们共育有三女一子:亨里埃特 Henriette (1880年)、艾达 Ida (1884年)、爱尔莎 Else (1891年)、亚瑟·路德维希 Arthur Ludwig (1881年)。[7]玻尔兹曼回到格拉茨担任实验物理学的主席。他在格拉茨的学生中有斯凡特·阿伦尼乌斯 Svante Arrhenius和瓦尔特·能斯特 Walther Nernst。[8][9]
他十分享受在格拉茨度过的14个春秋,正是在那里,他发展了他的自然界的统计概念。
玻尔兹曼于1890年被任命为德国巴伐利亚慕尼黑大学理论物理学主席。
1894年,波尔兹曼接替他的老师约瑟夫·斯特凡 Joseph Stefan成为维也纳大学理论物理学教授。
晚年生活与逝世缘由
晚年的玻尔兹曼致力于维护自己所创立的理论。[10] 在维也纳,他和一些同事相处不很融洽,尤其是恩斯特·马赫 Ernst Mach (1895年成为哲学和科学史教授)。1895年,格奥尔格·赫尔姆 Georg Helm和威廉·奥斯特瓦尔德 Wilhelm Ostwald 在吕贝克的一次会议上提出了他们关于能量学的观点。他们认为宇宙的主要组成部分是能量,而不是物质。会议辩论中,玻尔兹曼的观点赢得了其他支持原子理论的物理学家的赞同。[11] 在威廉·奥斯特瓦尔德的邀请下,玻尔兹曼于1900年前往莱比锡大学,填补辞世的古斯塔夫·海因里希·维德曼 Gustav Heinrich Wiedemann留下的空缺,出任物理学首席教授。在马赫因健康原因退休以后,玻尔兹曼于1902年返回维也纳。[10] 1903年,玻尔兹曼与古斯塔夫·冯·埃舍里希 Gustav von Escherich、埃米尔·穆勒 Emil Müller一同创立了奥地利数学学会。他的门生包括:卡尔·普里贝拉姆 Karl Přibram(经济学家),保罗·埃伦费斯特 Paul Ehrenfest(理论物理学家),丽斯·迈特纳 Lise Meitner(物理学家,被爱因斯坦称为“德国居里夫人”)。[10]
在维也纳大学,玻尔兹曼教授物理和哲学。他有关自然哲学的讲座颇受欢迎。开课当天,即使已经事先安排了最大的讲堂,现场依然是座无虚席,观者如山。讲座取得巨大成功,轰动全国,奥匈帝国皇帝也邀请玻尔兹曼入宫进行招待。[12]
1906年,玻尔兹曼日渐恶化的精神状况迫使他辞去教职。后人对他当时的症状进行分析得出了躁郁症的结论。[10][13]四个月后,在和妻女的度假过程中,他选择上吊自杀结束自己的痛苦和生命,终年63岁。[14][15][16][13]
他葬在维也纳中央弗里德霍夫墓园。墓碑上刻着玻尔兹曼熵公式: [math]\displaystyle{ S = k \cdot \log W }[/math][10]
哲学观点
玻尔兹曼的气体动力学理论似乎假定了原子和分子的真实性,但几乎所有德国哲学家和许多科学家,如恩斯特·马赫和物理化学家威廉·奥斯特瓦尔德,都不相信它们的存在。[17] 在19世纪90年代,玻尔兹曼试图形成一个折中立场,使原子主义者和反原子主义者都可以在不争论原子存在与否的情况下研究物理学。他的解决方案是使用赫兹的理论,即原子是‘Bilder’,即模型或图片。原子论者可以认为这些图像是真实的原子,而反原子论者则认为这些图像代表了一种有用但不真实的模型,然而这两类人都不完全满意。此外,由于玻尔兹曼关于原子和分子真实存在的假设,特别是对于热力学第二定律的统计解释,奥斯特瓦尔德和许多“纯热力学”的捍卫者试图努力驳斥气体动力学理论和统计力学。
在世纪之交,玻尔兹曼的理论受到另一种哲学的威胁。一些物理学家,包括马赫的学生古斯塔夫·乔曼,把赫兹的理论解释为——所有的电磁行为都是连续的,就好像没有原子和分子的存在,同样所有的物理行为最终都是电磁性质的。1900年左右的这一运动使玻尔兹曼深感沮丧,因为这可能意味着他的动力学理论和热力学第二定律的统计解释的终结。
1901年马赫在维也纳辞职后,玻尔兹曼回到学校,并决定自己成为一名哲学家,以驳斥哲学上对物理学的异议,但他很快又受到了打击。1904年,在圣路易斯举行的一次物理会议上,大多数物理学家似乎都拒绝接受原子,他甚至没有被邀请参加物理部分。相反,他被困在“应用数学”的讨论会,他猛烈地攻击哲学,特别是在所谓的达尔文主义的基础上,但实际上是根据拉马克的后天特征遗传理论,人们从过去继承了糟糕的哲学,科学家很难克服这种遗传。
1905年,玻尔兹曼与德-奥哲学家弗朗茨·布伦塔诺 Franz Brentano进行了广泛的通信,希望能更好地掌握哲学,显然,这样他就能更好地驳斥哲学在科学上的相关性,但他对这种方法也逐渐感到沮丧。
物理学贡献
玻尔兹曼最重要的科学贡献是在动力学理论上,包括推动应用麦克斯韦-玻尔兹曼分布 Maxwell–Boltzmann distribution 描述气体中分子的速度。直至今日,麦克斯韦-玻尔兹曼统计 Maxwell–Boltzmann statistics 和玻尔兹曼分布 Boltzmann distribution 仍然是经典统计力学基石之一。他们也适用于解释其他不需要量子统计的现象,另外提供了关于温度内涵的洞见。
自1808年,约翰·道尔顿 John Dalton 提出原子理论以来、包括詹姆斯·克拉克·麦克斯韦 James Clerk Maxwell(苏格兰)和乔赛亚·威拉德·吉布斯 Josiah Willard Gibbs(美)在内,大多数化学家都认同玻尔兹曼对原子和分子的看法,但很多物理学家直到几十年后才认同这一观点。玻尔兹曼与当时著名的德国物理学杂志的编辑有长期的争执,后者拒绝让玻尔兹曼将原子和分子作为方便的理论结构之外的任何东西。玻尔兹曼去世几年后,佩兰 Perrin基于爱因斯坦 Einstein1905年的理论研究,对胶体悬浮液进行了研究(1908-1909),证实了阿伏伽德罗数 Avogadro's number和玻尔兹曼常数的值,使世界相信微小粒子确实存在。
普朗克曾说:“熵和概率之间的对数关系是由玻尔兹曼在他的气体动力学理论中首次提出的”。[18] 也就是著名的熵公式:[19][20][math]\displaystyle{ S = k_B \ln W }[/math],其中kB 是玻尔兹曼常数,W 代表德文中宏观状态出现的概率,[21]更准确一些来说,是对应于系统宏观状态的可能微观状态的数量——在一个系统的(可观察的)热力学状态下的(不可观测的)“方式”的数量,可以通过分配不同的位置和动量给不同的分子来实现。玻尔兹曼的范式是N个相同粒子的理想气体,其中Ni处于第i个微观位置和动量条件(范围)。W 可以用排列公式计算:[math]\displaystyle{ W = N! \prod_i \frac{1}{N_i!} }[/math],其中i 的范围包含所有可能的分子状态,[math]\displaystyle{ ! }[/math]代表阶乘。分母中的“修正”解释了相同条件下难以区分的粒子。
玻尔兹曼也被认为是量子力学的先驱之一,因为他在1877年提出了物理系统的能级可以是离散的。
玻尔兹曼方程
建立玻尔兹曼方程是用来描述理想气体的动力学规律的。
其中 ƒ 代表某一时刻单个粒子位置和动量的函数分布(见麦克斯韦-玻尔兹曼方程|麦克斯韦-玻尔兹曼分布),F 代表力,m 代表粒子的质量,t 是时间,v 是粒子的平均速度。
该方程描述了单粒子相空间中一团点密度分布的位置和动量概率分布的时空变化(见哈密顿力学 Hamiltonian mechanics)。左边的第一项表示分布函数的显式时间变化,而第二项给出空间变化,第三项描述作用于粒子的任何力响。方程右边表示碰撞的影响。
原则上,在给定适当的边界条件下,上述方程完全描述了气体粒子系综的动力学。这个一阶微分方程看似简单的,因为ƒ可以表示一个任意的单粒子分布函数。另外,作用在粒子上的力直接取决于速度分布函数ƒ。然而玻尔兹曼方程是出了名的难以进行积分。大卫·希尔伯特 David Hilbert花了数年时间试图解决这个问题,但没有实现任何真正的突破。
玻尔兹曼假设的碰撞项的形式是近似的。然而,对于理想气体,玻尔兹曼方程的标准查普曼-恩斯库格解是非常精确的;只有在激波条件下才会得到错误的结果。
玻尔兹曼多年来一直试图用他的气体动力学方程——著名的“H”定理来“证明”热力学第二定律。然而,他在公式化碰撞项时所做的关键假设是“分子混沌”,该假设打破了时间反转对称性,这对于任何可能指向第二定律的内容都是必要的。玻尔兹曼表面上的成功仅仅来自概率假设,所以他与洛施密特 Loschmidt和其他人就洛施密特悖论 Loschmidt's paradox 的长期争论最终以他的失败告终。
最后,在20世纪70年代E.G.D. Cohen和J. R. Dorfman证明了玻尔兹曼方程在高密度上的系统(幂级数)推广在数学上是不可能的。因此,稠密气体和液体的非平衡统计力学 nonequilibrium statistical mechanics侧重于格林-久保亮五关系 Green–Kubo relations、涨落定理 Fluctuation theorem 和其他方法。
玻尔兹曼:“热力学第二定律是无序定律”
波尔兹曼认为热力学第二定律或“熵定律”是无序定律(或动态有序状态是“无限不可能的”)。
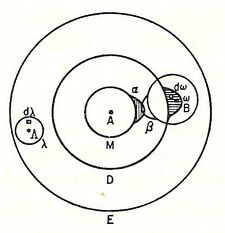
具体来讲,玻尔兹曼试图将其简化为随机碰撞函数,或机械粒子随机碰撞后的概率定律。继麦克斯韦之后[22] ,玻尔兹曼把气体分子模拟成一个盒子里碰撞的台球,并指出每一次碰撞非平衡态速度分布(多组分子运动的速度和方向相同)会越来越无序,并导致最终的宏观均匀和微观最无序或最大熵状态(宏观均匀的状态对应所有场势或梯度的消失)。[23]因此,他认为,热力学第二定律描述了这样一个事实结果:在一个机械碰撞粒子的世界里,无序状态是最有可能的。因为可能的无序状态比有序状态要多得多,一个系统几乎总是会处于最无序状态——具有最多可接近的微观状态的宏观状态,如处于平衡状态的盒子里的气体——或向最无序状态移动。因此,玻尔兹曼总结道,一个动态有序的状态,即分子以“相同的速度和相同的方向”运动,是“最不可思议的可能情况…… 一种无限不可能的能量配置”。[24]
玻尔兹曼完成了证明热力学第二定律只是一个统计事实的壮举。能量的逐渐无序化类似于一叠最初有序排列的卡牌重复洗牌过程中变得无序,也正如经历了无数次洗牌而重归初始有序状态的卡牌一样,我们的宇宙最终将在某一时刻回到最初的状态。(当人们试图估计宇宙正在消亡的时间线时,这种乐观的结论就显得有些平淡了,因为时间线很可能在它自然发生之前就已经过去了。)[25]熵增加的趋势似乎对初学热力学的人们造成困难,但从概率论的观点出发就很容易理解。考虑两个普通的骰子,都是正面朝上的。摇骰子后,发现这两个6面都朝上的概率很小(1/36);因此,我们可以说,骰子的随机运动,就像分子由于热能的混乱碰撞,会导致系统从概率较小的状态变为概率较大的状态。数以百万计的骰子,就像热力学计算中数以百万计的原子一样,它们全部为6的概率变得如此之小,以至于系统必须移动到一个更可能的状态。[26]然而,数学上出现所有骰子结果都是6或者都不是6的几率都很小,由于统计数据会趋于平衡,每36对骰子会有一对6出现,而洗过的牌有时会呈现出某种临时的顺序,即使整个牌是无序的。
获奖经历与荣誉
1885年,他成为奥地利帝国科学院的成员,1887年,他成为格拉茨大学的校长。1888年,他被选为瑞典皇家科学院成员,1899年被选为皇家学会外国成员。[27]另外许多事物都以他的名字命名。
另见
- 能量学
- 玻尔兹曼大脑
参考文献及注释
- ↑ Klein, Martin (1970). "Boltzmann, Ludwig". In Preece, Warren E. (in English). Encyclopædia Britannica (hard cover). 3 (Commemorative Edition for Expo 70 ed.). Chicago: William Benton. p. 893a. ISBN 0852291353.
- ↑ Partington, J.R. (1949), An Advanced Treatise on Physical Chemistry, vol. volume 1, Fundamental Principles, The Properties of Gases, London: Longmans, Green and Co., p. 300
{{citation}}:|volume=has extra text (help) - ↑ Gibbs, Josiah Willard (1902). Elementary Principles in Statistical Mechanics. New York: Charles Scribner's Sons.
- ↑ Simmons, John; Simmons, Lynda (2000). The Scientific 100. Kensington Publishing Corp.. p. 123. ISBN 9780806536781.
- ↑ 5.0 5.1 James, Ioan (2004). Remarkable Physicists: From Galileo to Yukawa. Cambridge University Press. p. 169. ISBN 9780521017060. https://archive.org/details/remarkablephysic00jame.
- ↑ Južnič, Stanislav (December 2001). "Ludwig Boltzmann in prva študentka fizike in matematike slovenskega rodu" [Ludwig Boltzmann and the First Student of Physics and Mathematics of Slovene Descent]. Kvarkadabra.net (in Slovenian) (12). Retrieved 17 February 2012.
{{cite journal}}: CS1 maint: unrecognized language (link) - ↑ https://www.boltzmann.com/ludwig-boltzmann/biography/
- ↑ Jäger, Gustav; Nabl, Josef; Meyer, Stephan (April 1999). "Three Assistants on Boltzmann". Synthese. 119 (1–2): 69–84. doi:10.1023/A:1005239104047.
Paul Ehrenfest (1880–1933) along with Nernst, Arrhenius, and Meitner must be considered among Boltzmann's most outstanding students.
- ↑ "Walther Hermann Nernst". Archived from the original on 2008-06-12.
Walther Hermann Nernst visited lectures by Ludwig Boltzmann
- ↑ 10.0 10.1 10.2 10.3 10.4 Cercignani, Carlo (1998) Ludwig Boltzmann: The Man Who Trusted Atoms. Oxford University Press.
- ↑ Max Planck (1896). "Gegen die neure Energetik". Annalen der Physik. 57 (1): 72–78. Bibcode:1896AnP...293...72P. doi:10.1002/andp.18962930107.
- ↑ The Boltzmann Equation: Theory and Applications, E.G.D. Cohen, W. Thirring, ed., Springer Science & Business Media, 2012
- ↑ 13.0 13.1 Nina Bausek and Stefan Washietl. "Tragic deaths in science: Ludwig Boltzmann — a mind in disorder". Paperpile. Retrieved 2020-04-26.
- ↑ "Eureka! Science's greatest thinkers and their key breakthroughs", Hazel Muir, p.152,
- ↑ Boltzmann, Ludwig (1995). "Conclusions". In Blackmore, John T.. Ludwig Boltzmann: His Later Life and Philosophy, 1900-1906. 2. Springer. pp. 206–207. ISBN 978-0-7923-3464-4. https://books.google.com/books?id=apip-Jm9WuwC&pg=PA207.
- ↑ Upon Boltzmann's death,Friedrich ("Fritz") Hasenöhrl became his successor in the professorial chair of physics at Vienna.
- ↑ Bronowski, Jacob (1974). "World Within World". The Ascent Of Man. Little Brown & Co. p. 265. ISBN 978-0-316-10930-7. https://archive.org/details/ascentofmanbron00bron.
- ↑ Max Planck, p. 119.
- ↑ The concept of entropy was introduced by Rudolf Clausius in 1865. He was the first to enunciate the second law of thermodynamics by saying that "entropy always increases".
- ↑ An alternative is the information entropy definition introduced in 1948 by Claude Shannon.[1] It was intended for use in communication theory, but is applicable in all areas. It reduces to Boltzmann's expression when all the probabilities are equal, but can, of course, be used when they are not. Its virtue is that it yields immediate results without resorting to factorials or Stirling's approximation. Similar formulas are found, however, as far back as the work of Boltzmann, and explicitly in Gibbs (see reference).
- ↑ Pauli, Wolfgang (1973). Statistical Mechanics. Cambridge: MIT Press. ISBN 978-0-262-66035-8., p. 21
- ↑ Maxwell, J. (1871). Theory of heat. London: Longmans, Green & Co.
- ↑ Boltzmann, L. (1974). The second law of thermodynamics. Populare Schriften, Essay 3, address to a formal meeting of the Imperial Academy of Science, 29 May 1886, reprinted in Ludwig Boltzmann, Theoretical physics and philosophical problem, S. G. Brush (Trans.). Boston: Reidel. (Original work published 1886)
- ↑ Boltzmann, L. (1974). The second law of thermodynamics. p. 20
- ↑ "Collier's Encyclopedia", Volume 19 Phyfe to Reni, "Physics", by David Park, p. 15
- ↑ "Collier's Encyclopedia", Volume 22 Sylt to Uruguay, Thermodynamics, by Leo Peters, p. 275
- ↑ "Fellows of the Royal Society". London: Royal Society. Archived from the original on 2015-03-16.
拓展阅读
- Roman Sexl & John Blackmore (eds.), "Ludwig Boltzmann – Ausgewahlte Abhandlungen", (Ludwig Boltzmann Gesamtausgabe, Band 8), Vieweg, Braunschweig, 1982.
- John Blackmore (ed.), "Ludwig Boltzmann – His Later Life and Philosophy, 1900–1906, Book One: A Documentary History", Kluwer, 1995.
- John Blackmore, "Ludwig Boltzmann – His Later Life and Philosophy, 1900–1906, Book Two: The Philosopher", Kluwer, Dordrecht, Netherlands, 1995.
- John Blackmore (ed.), "Ludwig Boltzmann – Troubled Genius as Philosopher", in Synthese, Volume 119, Nos. 1 & 2, 1999, pp. 1–232.
- Blundell, Stephen; Blundell, Katherine M. (2006). Concepts in Thermal Physics. Oxford University Press. p. 29. ISBN 978-0-19-856769-1. https://books.google.com/books?id=vuBHXwAACAAJ.
- Boltzmann, Ludwig Boltzmann – Leben und Briefe, ed., Walter Hoeflechner, Akademische Druck- u. Verlagsanstalt. Graz, Oesterreich, 1994
- Brush, Stephen G. (ed. & tr.), Boltzmann, Lectures on Gas Theory, Berkeley, California: U. of California Press, 1964
- Brush, Stephen G. (ed.), Kinetic Theory, New York: Pergamon Press, 1965
- Brush, Stephen G. (1970). "Boltzmann". In Charles Coulston Gillispie. Dictionary of Scientific Biography. New York: Scribner. ISBN 978-0-684-16962-0. https://archive.org/details/dictionaryofsci001gill.
- Brush, Stephen G. (1986). The Kind of Motion We Call Heat: A History of the Kinetic Theory of Gases. Amsterdam: North-Holland. ISBN 978-0-7204-0370-1.
- Cercignani, Carlo (1998). Ludwig Boltzmann: The Man Who Trusted Atoms. Oxford University Press. ISBN 9780198501541. https://archive.org/details/ludwigboltzmannm0000cerc.
- Darrigol, Olivier (2018). Atoms, Mechanics, and Probability: Ludwig Boltzmann's Statistico-Mechanical. Oxford University Press. ISBN 978-0-19-881617-1. https://books.google.com/books?id=APBIDwAAQBAJ&pg=PA376.
- Ehrenfest, P.& Ehrenfest, T. (1911) "Begriffliche Grundlagen der statistischen Auffassung in der Mechanik", in Encyklopädie der mathematischen Wissenschaften mit Einschluß ihrer Anwendungen Band IV, 2. Teil ( F. Klein and C. Müller (eds.). Leipzig: Teubner, pp. 3–90. Translated as The Conceptual Foundations of the Statistical Approach in Mechanics. New York: Cornell University Press, 1959.
- Everdell, William R (1988). "The Problem of Continuity and the Origins of Modernism: 1870–1913". History of European Ideas. 9 (5): 531–552. doi:10.1016/0191-6599(88)90001-0.
- Everdell, William R (1997). The First Moderns. Chicago: University of Chicago Press. https://archive.org/details/firstmodernsprof00ever.
- Gibbs, Josiah Willard (1902). Elementary Principles in Statistical Mechanics, developed with especial reference to the rational foundation of thermodynamics. New York: Charles Scribner's Sons.
- Johnson, Eric (2018). Anxiety and the Equation: Understanding Boltzmann's Entropy. The MIT Press. ISBN 978-0-262-03861-4.
- Klein, Martin J. (1973). "The Development of Boltzmann's Statistical Ideas". In E.G.D. Cohen. The Boltzmann Equation: Theory and Applications. Acta physica Austriaca Suppl. 10. Wien: Springer. pp. 53–106. ISBN 978-0-387-81137-6. https://archive.org/details/boltzmannequatio00schm.
- Lindley, David (2001). Boltzmann's Atom: The Great Debate That Launched A Revolution In Physics. New York: Free Press. ISBN 978-0-684-85186-0. https://archive.org/details/isbn_9780684851860.
- Lotka, A. J. (1922). "Contribution to the Energetics of Evolution". Proc. Natl. Acad. Sci. U.S.A. 8 (6): 147–51. Bibcode:1922PNAS....8..147L. doi:10.1073/pnas.8.6.147. PMC 1085052. PMID 16576642.
- Meyer, Stefan (1904) (in German). Festschrift Ludwig Boltzmann gewidmet zum sechzigsten Geburtstage 20. Februar 1904. J. A. Barth. https://archive.org/details/festschriftludw00meyegoog.
- Planck, Max (1914). The Theory of Heat Radiation. P. Blakiston Son & Co. https://archive.org/details/theoryofheatradi00planrich. English translation by Morton Masius of the 2nd ed. of Waermestrahlung. Reprinted by Dover (1959) & (1991).
- Tolman, Richard C. (1938). The Principles of Statistical Mechanics. Oxford University Press. Reprinted: Dover (1979).
外部链接
- Uffink, Jos (2004). "Boltzmann's Work in Statistical Physics". Stanford Encyclopedia of Philosophy. Retrieved 11 June 2007.
- Ruth Lewin Sime, Lise Meitner: A Life in Physics Chapter One: Girlhood in Vienna gives Lise Meitner's account of Boltzmann's teaching and career.
- Eftekhari, Ali, "Ludwig Boltzmann (1844–1906)." Discusses Boltzmann's philosophical opinions, with numerous quotes.
- Rajasekar, S.; Athavan, N. (2006-09-07). "Ludwig Edward Boltzmann". arXiv:physics/0609047.
编者推荐
为什么时间是一条单行道 ? Why time is one-way street?
爱因斯坦对热力学第二定律不是很关心,但是他很关心空间和时间的问题,他曾说过,将时间和空间放到一起就会构成一个共同体就是时空,时间和空间是紧密联系在一起的。我们都知道空间的坐标都是对称的,物理定律也都是对称的,为什么我们的世界却如此的不对称呢?对于时间的不对称,我们会产生很多困惑:
- 时间是什么?
- 时间的本质是什么?
- 时间可以倒流吗?
- 宇宙的命运是什么?
- 为什么时间是单行道?
斯坦福大学理论物理学主任,弦理论创始人之一,Leonard Susskind老师从玻尔兹曼盒子,到分形流,以及时间流向的说法,为你解释宇宙和时间的奥秘。
其他
- 知乎朋友「贾明子」魔鬼眼中的自然界。https://zhuanlan.zhihu.com/c_116602381?group_id=884931161871237120
本中文词条由Swarma参与编译,栗子CUGB审校,糖糖编辑,如有问题,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。