鸟群算法 Boids
鸟群算法( Boids)是模拟鸟类群集行为的人工生命项目,由克雷格·雷诺兹 Craig Reynolds于1986年开发。该模型常用于计算机动画或计算机辅助设计的计算机三维几何。他关于这个主题的论文发表在1987年的 ACM SIGGRAPH(美国计算机协会计算机图形专业组组织的计算机图形学顶级年度会议)会议记录上。[1]“ boid”是“ bird-oid object”的缩写,指一个类鸟对象。[2]恰巧,“boid”也是纽约都市方言中“bird”的发音。
算法介绍
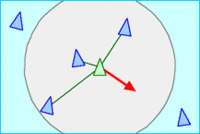
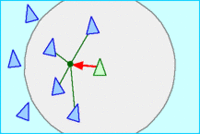
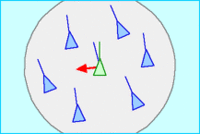
与大多数人工生命模拟一样,Boids 是涌现行为的一个例子; 也就是说,Boids 的复杂性来自于遵循一系列简单规则个体 agents(这里是 Boids)的相互作用。在最简单的Boids世界中适用的规则如下,其描述了鸟群中的个体如何根据周边同伴的位置和速度移动:
- 分离 Separation: 移动以避开群体拥挤处
- 对齐 Alignment: 朝着周围同伴的平均方向前进
- 靠近 Cohesion: 朝着周围同伴的平均位置(质心)移动
每个 boid 个体都可以得知整体的几何参数,但群体要求其只对其周围某个小邻近范围作出反应。该邻近范围由一个距离(从该个体的中心算起)和一个角度(从其飞行方向算起)决定。此范围外的同伴不予考虑。该临近范围可以认为是一个有限知觉的模型(就像浑水中的鱼一样);但更恰当的想法可能是,其定义了鸟群影响了个体转向的区域范围。
当然也可以添加更复杂的规则,如避障和寻找目标。
该基本模型自Reynolds提出以来,已用多种方法扩展。例如,Delgado-Mata [3]等人扩展基本模型以加入恐惧的影响。因为动物之间靠嗅觉来传递情感,所以他利用一种可自由膨胀气体中的粒子来模拟信息素。哈特曼 Hartman和贝内斯 Benes[4]我们为这种结盟引入了互补的力量,称之为领导力更替。这个力决定了这个鸟成为领导者或者试图逃脱群体的概率。
Boids 的运动可以表现为混乱(分裂的群体和狂野的行为)或有序。意想不到的行为比如群体分散和避开障碍后的集聚,可以被认为是涌现的。
Boids 框架通常用于计算机图形学,提供鸟群和其他生物(如鱼群)的逼真表现。例如,在1998年的电子游戏《半条命 Half-Life》中,游戏结束时Xen中出现的类似鸟类的飞行生物就使用了该框架(游戏文件中命名为“ boid”)。
Boids 模型可用于集群机器人 Swarm Robotics中简单的无人地面车辆(UGV)[5] 或微型飞行器 Micro Aerial Vehicles(MAV)[6]群体的直接控制和稳定。为了异质 UAV-UGV 群体的稳定性,Saska 等人将该模型用于板载相对定位。[7]
在当时提出时,Reynolds的方法相比于传统的计算机动画电影技术是一个巨大的进步。第一部利用了此模型的动画片是《史丹利和史黛拉: 破冰 Stanley and Stella in: Breaking The Ice》(1987),之后是蒂姆·伯顿 Tim Burton的故事片《蝙蝠侠归来 Batman Returns》(1992),电脑合成的蝙蝠群和成群的企鹅行进穿过哥谭市 Gotham City的街道。[8]
Boids 模型已经被用于其他有趣应用。该系统已应用于互联网多频道广播电台的自动节目编排,它也被用于可视化信息和优化任务。[9]以及可视化信息[10]和优化任务。[11]
代码实现
以下内容是使用BOIDS三层模型对鸟群运动进行了模拟,可以通过调节不同的参数获取到不同的实验现象,可以在这个基础上修改模型规则,以更好的模拟集群运动,本文提供一个模板。代码来源是沐雨橙风fire所写的博客。
# -*- coding:utf-8 -*-
import argparse
import math
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from scipy.spatial.distance import squareform, pdist
from numpy.linalg import norm
width, height = 1920, 1080
N = 100 # number of birds
minDist = 100.0 # min dist of approach
maxRuleVel = 0.3 # max magnitude of velocities calculated by "rules"
maxVel = 3.0 # max magnitude of final velocity
class Birds:
"""
Simulates flock behaviour of birds, using the realistic-looking Boids model (1986)
"""
def __init__(self):
self.N = N
self.minDist = minDist
self.maxRuleVel = maxRuleVel
self.maxVel = maxVel
# Computing initial position and velocity
self.pos = [width / 2.0, height / 2.0] + 10 * np.random.rand(2 * N).reshape(N, 2)
# Create an array of N random variable angles in the range [0. 2pi]
angles = 2 * math.pi * np.random.rand(N)
# Random velocity vector [x,y] coordinates zip grouped
self.vel = np.array(list(zip(np.sin(angles), np.cos(angles))))
def savef(self):
with open("douban.txt", "a") as f:
f.write(str(self.pos.reshape(1, N*2)))
print str(self.pos.reshape(1, N*2))
f.close()
def tick(self, frameNum, pts, beak):
"""
Update the simulation by one time step
"""
# get pairwise distances
self.distMatrix = squareform(pdist(self.pos))
# apply rules:
self.vel += self.apply_rules()
self.limit(self.vel, self.maxVel)
self.pos += self.vel
self.apply_bc()
# update data
pts.set_data(self.pos.reshape(2 * self.N)[::2],
self.pos.reshape(2 * self.N)[1::2])
vec = self.pos + 10 * self.vel / self.maxVel
beak.set_data(vec.reshape(2 * self.N)[::2],
vec.reshape(2 * self.N)[1::2])
self.savef()
#print self.pos.reshape(2 * self.N)
#np.savetxt("x.txt", self.pos.reshape(1, 2*N))
def limit_vec(self, vec, max_val):
""" Limit magnitude of 2D vector """
mag = norm(vec)
if mag > max_val:
vec[0], vec[1] = vec[0] * max_val / mag, vec[1] * max_val / mag
def limit(self, x, max_val):
""" Limit magnitide of 2D vectors in array X to maxValue """
for vec in x:
self.limit_vec(vec, max_val)
def apply_bc(self):
""" Apply boundary conditions """
deltaR = 2.0
for coord in self.pos:
if coord[0] > width + deltaR:
coord[0] = - deltaR
if coord[0] < - deltaR:
coord[0] = width + deltaR
if coord[1] > height + deltaR:
coord[1] = - deltaR
if coord[1] < - deltaR:
coord[1] = height + deltaR
def apply_rules(self):
# apply rule #1 - Separation
D = self.distMatrix < 20.0
vel = self.pos * D.sum(axis=1).reshape(self.N, 1) - D.dot(self.pos)
self.limit(vel, self.maxRuleVel)
# different distance threshold
D = self.distMatrix < 50.0
# apply rule #2 - Alignment
vel2 = D.dot(self.vel)
self.limit(vel2, self.maxRuleVel)
vel += vel2
# apply rule #1 - Cohesion
vel3 = D.dot(self.pos) - self.pos
self.limit(vel3, self.maxRuleVel)
vel += vel3
return vel
def tick(frameNum, pts, beak, birds):
""" Update function for animation """
birds.tick(frameNum, pts, beak)
return pts, beak
def main():
print('Starting flock simulation...')
# Create birds
birds = Birds()
# Setup plot
fig = plt.figure()
ax = plt.axes(xlim=(0, width), ylim=(0, height))
pts, = ax.plot([], [], markersize=10, c='k', marker='o', ls='None')
beak, = ax.plot([], [], markersize=4, c='r', marker='o', ls='None')
anim = animation.FuncAnimation(fig, tick, fargs=(pts, beak, birds), interval=20)
# TODO: add a "button press" event handler to scatter birds
#anim.save('basic_animation.mp4', fps=30, extra_args=['-vcodec', 'libx264'])
plt.show(anim)
if __name__ == '__main__':
main()
参见
- 群体智能 Swarm intelligence
参考文献
- ↑ Reynolds, Craig (1987). Flocks, herds and schools: A distributed behavioral model.. Association for Computing Machinery. pp. 25–34. doi:10.1145/37401.37406. ISBN 978-0-89791-227-3.
- ↑ Banks, Alec; Vincent, Jonathan; Anyakoha, Chukwudi (July 2007). "A review of particle swarm optimization. Part I: background and development". Natural Computing. 6 (4): 467–484. CiteSeerX 10.1.1.605.5879. doi:10.1007/s11047-007-9049-5.
- ↑ Delgado-Mata, Carlos; Martinez, Jesus Ibanez; Bee, Simon; Ruiz-Rodarte, Rocio; Aylett, Ruth (2007). "On the use of Virtual Animals with Artificial Fear in Virtual Environments". New Generation Computing. 25 (2): 145–169. doi:10.1007/s00354-007-0009-5.
- ↑ Hartman, Christopher; Benes̆, Bedr̆ich (July 2006). "Autonomous boids". Computer Animation and Virtual Worlds. 17 (3–4): 199–206. doi:10.1002/cav.123.
- ↑ Min, Hongkyu; Wang, Zhidong (2011). Design and analysis of Group Escape Behavior for distributed autonomous mobile robots. IEEE International Conference on Robotics and Automation (ICRA). doi:10.1109/ICRA.2011.5980123.
- ↑ Saska, Martin; Jan, Vakula; Libor, Preucil (2014). Swarms of micro aerial vehicles stabilized under a visual relative localization. IEEE International Conference on Robotics and Automation (ICRA). doi:10.1109/ICRA.2014.6907374.
- ↑ Saska, Martin; Vojtech, Vonasek; Tomas, Krajnik; Libor, Preucil (2012). Coordination and Navigation of Heterogeneous UAVs-UGVs Teams Localized by a Hawk-Eye Approach (PDF). IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS).
- ↑ Lebar Bajec, Iztok; Heppner, Frank H. (2009). "Organized flight in birds" (PDF). Animal Behaviour. 78 (4): 777–789. doi:10.1016/j.anbehav.2009.07.007.
- ↑ Ibáñez, Jesús; Gómez-Skarmeta, Antonio F.; Blat, Josep (2003). DJ-boids: emergent collective behavior as multichannel radio station programming. pp. 248–250. doi:10.1145/604045.604089.
{{cite conference}}: Unknown parameter|booktitle=ignored (help) - ↑ Moere, A V (2004). Time-Varying Data Visualization Using Information Flocking Boids. pp. 97–104. doi:10.1109/INFVIS.2004.65.
{{cite conference}}: Unknown parameter|booktitle=ignored (help) - ↑ Cui, Zhihua; Shi, Zhongzhi (2009). "Boid particle swarm optimisation". International Journal of Innovative Computing and Applications. 2 (2): 77–85. doi:10.1504/IJICA.2009.031778.
外部链接
- Live In-Browser 3D Simulation of Bird Flocking Behavior in Unity3D – Open Source implementation for Windows, Linux and Mac
编者推荐
集智相关课程
透过人工鸟群Boid模型学习List的使用
讲师:张江(北师大系统科学学院教授、博士生导师,集智俱乐部、集智学园创始人。)
本课程通过数个案例教会大家如何去动手搭建一个多主体仿真模型,以及如何利用NetLogo去实现。从生命游戏到人工鸟群,从模拟经济系统到病毒沿网络的传播,通过循序渐进的案例,该课程带你逐步走入NetLogo多主体建模的神奇世界。
集智相关文章
张江:乌合之众还是群智涌现?鸟群知道答案
生命如何起源,智能如何涌现,因果如何反转,复杂谜题,引人深思。2019年7月13日,集智俱乐部创始人张江教授在混沌大学授课,详细解读了复杂系统中的混沌、涌现与进化,此文整理自课堂内容。
其他
动画片《Stanley and Stella in: Breaking the Ice (1987)》
Craig Reynolds 与 Symbolics Graphics 和 Whitney / Demos Production 的同事合作制作的利用 boids 模型的小短片,讲述了飞鸟与鱼相爱,鸟儿冲破冰面与鱼相见的故事。影片最早于87年在 SIGGRAPH 电子剧院展出。
本中文词条由Dorr参与编译,木子二月鸟审校,薄荷编辑,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。