模块度
模块度 Modularity是对网络结构或图像结构的一种度量。它是一种衡量网络模板(也称为节点集或社团)划分质量的标准。如果模板度高,则说明节点集内部连接紧密,而节点集与节点集之间连接稀疏。模块度是检测社团结构 Community Structure的常用优化方法。不过,受分辨率的限制,该方法不适用于检测小社团。
起源
许多重要的科学问题可以通过网络来呈现,并进行实证研究。 生物模式和社会模式、万维网、代谢网络、食物网、神经网络和病理网络这类现实问题,都可以通过数学表示和拓扑学研究来发现一些意想不到的结构特征。 这些网络大都具有某种社团结构,这种结构能够帮助人们更加理解网络中的动态过程。 例如,与连接稀疏的社会群体相比,连接紧密的社会群体之间传播信息或谣言的速度更快。 如果一个网络由若干个单独节点组成,这些节点之间通过链接相互联系,这表示节点之间有一定程度的相互作用,故将社团定义为内部连接紧密的节点组(而组与组之间连接稀疏)。对于一般的网络而言,由于社团可能具有完全不同的属性,如节点度、集聚系数、介数中心性、度分布等,所以如何检测网络中的社团极为重要。 模块度就是这样一种度量,当模块度最大时,就能够检测到给定网络的社团结构。
定义
模块度是指落在同一组的边的比例 ,即对这些边进行随机分配所得到的期望概率(将边随机分配是为了保持每个节点的节点度不变)。其中,落在同一组的边的比例=组内的总边数÷网络中的总边数。无权图和无向图的模块度取值都在[math]\displaystyle{ [-1/2,1] }[/math]范围内。如果节点组中的连边数量超过了随机分配时所得到的期望连边数量,模块度为正数。没有超过,则为负数。将给定网络的节点划分为若干模块,模块度反映的是模块内部连边的集中程度,而不是各模块之间所有节点链路的随机分布情况。
模块度的计算方法
模块度的计算有很多种方法。考虑一个含有[math]\displaystyle{ n }[/math]个节点、[math]\displaystyle{ m }[/math] 条连边的网络,这样的图网络能够用一个成员变量[math]\displaystyle{ s }[/math]划分为两个社团。如果节点[math]\displaystyle{ v }[/math]属于社团1,即设 [math]\displaystyle{ s_v = 1 }[/math],或节点 [math]\displaystyle{ v }[/math]属于社团2,即设[math]\displaystyle{ s_v = -1 }[/math]。 将图网络的邻接矩阵表示为 [math]\displaystyle{ A }[/math]。
[math]\displaystyle{ A_{{vw}}=0 }[/math]意味着节点[math]\displaystyle{ v }[/math] 和[math]\displaystyle{ w }[/math] 之间没有连边;[math]\displaystyle{ A_{vw} = 1 }[/math]则意味着节点v和节点w之间存在连边。
为便于理解,我们以无向网络为例。即有 [math]\displaystyle{ A_{vw} = A_{wv} }[/math]成立(需要指出的是,两个节点之间也可能存在多条连边,但这里仅讨论最简单的情况。)
模块度[math]\displaystyle{ Q }[/math]可定义为:在具有与给定网络相同度序列的随机化网络中,模板度等于在落在社团1或社团2中连边的比例—在社团1和社团2中将连边随机分布后所得到的概率期望。
两个节点间随机连边的概率期望求法
配置模型是一个特定网络的随机实现,我们利用配置模型的相关定义来计算连边随机分布后的概率期望。给定一个具有 [math]\displaystyle{ n }[/math]个节点的网络,其中设每个节点[math]\displaystyle{ v }[/math]的节点度为 [math]\displaystyle{ k_v }[/math],配置模型将每个连边切断并一分为二,切断的点称为末梢点。然后每一条半边(称为存根)随机与其他半边(除了自身)随机相连变成一条完整连边,并允许出现同一节点自我相连成环、两个节点间存在多条连边的情况。因此,即使网络的节点度序列保持不变,配置模型仍然是一个完全随机的网络。
现考虑节点[math]\displaystyle{ v }[/math]和节点[math]\displaystyle{ w }[/math],各自的节点度分别为 [math]\displaystyle{ k_v }[/math]和[math]\displaystyle{ k_w }[/math],在随机重新连边的网络中,利用上述方法计算这两个节点间所期望的完整连边数量。
其中,所有单边的数量为:
- [math]\displaystyle{ l = \sum_{u} k_{u} =2m }[/math]
我们考虑有[math]\displaystyle{ k_v }[/math] 条半边的节点[math]\displaystyle{ v }[/math] ,并设一个相关指示变量[math]\displaystyle{ I_i }[/math],其中。在给定[math]\displaystyle{ i = 1, \ldots, k_v }[/math]的随机化网络中,节点[math]\displaystyle{ v }[/math]的第[math]\displaystyle{ i }[/math]条半边恰好连接到节点[math]\displaystyle{ w }[/math](具有[math]\displaystyle{ k_w }[/math]条半边)的某条半边,此时[math]\displaystyle{ I_i = 1 }[/math]。如果没有连接到,则[math]\displaystyle{ I_i = 0 }[/math]。因为节点v的第i条半边可以等概率连接到剩下的任何 [math]\displaystyle{ 2m-1 }[/math]条半边,且[math]\displaystyle{ k_w }[/math]条半边也可以自我连接到节点[math]\displaystyle{ w }[/math]。
故可用公式:
- [math]\displaystyle{ p(I_i = 1) = E[I_i] = \frac{k_w}{2m-1} }[/math]
- [math]\displaystyle{ J_{vw} = \sum_i^{k_v}I_i }[/math]
- [math]\displaystyle{ E[J_{vw}] = E[\sum_iI_i] = \sum_i^{k_v}E[I_i] = \frac{k_v k_w}{2m - 1} }[/math]
对于有着大量连边的随机化网络,我们进行以下处理:当[math]\displaystyle{ m }[/math]很大时,我们将分母[math]\displaystyle{ 2m-1 }[/math]化简为[math]\displaystyle{ 2m }[/math],即利用 [math]\displaystyle{ \frac{k_v k_w}{2m} }[/math] 近似计算两个节点之间所期望的连边数量。此外,如果随机化网络的规模十分大,忽略发生同一节点自我相连成环、两个节点间存在多条连边的情况。我们设两个节点之间最多只有一条连边,此时 [math]\displaystyle{ J_{vw} }[/math] 变成二进制指示符变量,其期望值为 [math]\displaystyle{ J_{vw}=1 }[/math]的概率。这意味着,在节点v和节点w之间存在连边的期望概率为[math]\displaystyle{ \frac{k_v k_w}{2m} }[/math]。
因此,节点[math]\displaystyle{ v }[/math]和节点[math]\displaystyle{ w }[/math]之间的实际边数与它们在随机化网络下连边数的期望之差为[math]\displaystyle{ A_{vw} - \frac{k_v k_w}{2m} }[/math]。
公式表达一
按照模块度的定义,对于所有的节点对进行求和,即得模块度的计算公式为:
- [math]\displaystyle{ Q = \frac{1}{2m} \sum_{vw} \left[ A_{vw} - \frac{k_v k_w}{2m} \right] \frac{s_{v} s_{w}+1}{2} }[/math]
需要注意的是,上式只适用于将网络划分为两个社团的情况。将网络划分为两个社团,再将每个子社团进一步划分为两个较小的子社团,使得模块度达到最大化的划分方法称为层次划分。层次划分是一个能够识别网络中多个社团的可行方法。通常设将网络划分为c个社团。
公式表达二
模块度可以表示为:
- [math]\displaystyle{ Q = \frac{1}{2m} \sum_{vw} \left[ A_{vw} - \gamma\frac{k_v k_w}{2m}\right] \delta(c_{v}, c_{w}) }[/math]
其中:[math]\displaystyle{ Avw }[/math]为共引网络相邻矩阵的一个元素;[math]\displaystyle{ k_v }[/math]为节点[math]\displaystyle{ v }[/math]的度;[math]\displaystyle{ m }[/math]为网络中的连边总数;[math]\displaystyle{ c_v }[/math]为节点[math]\displaystyle{ v }[/math]被分配到的社团,如果[math]\displaystyle{ c_v=c_w }[/math],则函数[math]\displaystyle{ (c_v,c_w) }[/math]为1,否则为0。函数[math]\displaystyle{ Q }[/math]最大化即可得到最优社团划分。注意:[math]\displaystyle{ \gamma }[/math]是[math]\displaystyle{ Q }[/math]中的分辨率参数,标准模块函数中的[math]\displaystyle{ \gamma=1 }[/math]。较大的[math]\displaystyle{ \gamma }[/math]参数可检测出较小但较多的社团,较小的[math]\displaystyle{ \gamma }[/math]参数可检测出较大但较少的社团。需要说明的是,虽然社团数量的分布受到参数[math]\displaystyle{ \gamma }[/math]的影响,但动力学特性的显示几乎与社团分辨率无关。(摘自集智俱乐部微信公众号文章《Nature通讯:科学家兴趣转移愈发频繁,但对科研生涯可能不利》)
在标准模块函数中,[math]\displaystyle{ γ=1 }[/math],则有:
- [math]\displaystyle{ Q = \frac{1}{(2m)}\sum_{vw} \left[ A_{vw} - \frac{k_v k_w}{(2m)} \right] \delta(c_{v}, c_{w}) =\sum_{i=1}^{c} (e_{ij}-a_{i}^2) }[/math]
定义 [math]\displaystyle{ e_{ij} }[/math]为连接社团 [math]\displaystyle{ i }[/math]和 社团[math]\displaystyle{ j }[/math]的连边总数,则有:
- [math]\displaystyle{ e_{ij}= \sum_{vw} \frac{A_{vw}}{2m} 1_{v\in c_i} 1_{w\in c_j} }[/math]
[math]\displaystyle{ a_i }[/math]表示连接到社区[math]\displaystyle{ i }[/math]的连边总数,则有
- [math]\displaystyle{ a_i=\frac{k_i}{2m}= \sum_{j} e_{ij} }[/math]
公式表达三
模块度的另一种计算公式为:
- [math]\displaystyle{ Q = \frac{1}{2m} \sum_{vw} \sum_r \left[ A_{vw} - \frac{k_v k_w}{2m} \right] S_{vr} S_{wr} = \frac{1}{2m} \mathrm{Tr}(\mathbf{S}^\mathrm{T}\mathbf{BS}), }[/math]
在光谱优化算法中常被用到。如果节点[math]\displaystyle{ v }[/math]属于节点组[math]\displaystyle{ r }[/math] 则定义[math]\displaystyle{ Svr=1 }[/math],若不属于则为0。之后利用该公式进行代换计算:
- [math]\displaystyle{ \delta(c_v,c_w) = \sum_r S_{vr} S_{wr} }[/math]
其中[math]\displaystyle{ S }[/math]是包含元素[math]\displaystyle{ Svr }[/math]的矩阵(非方阵),而[math]\displaystyle{ B }[/math]是包含元素[math]\displaystyle{ B_{vw} = A_{vw} - \frac{k_v k_w}{2m} }[/math]的模块化矩阵。
由于模块化矩阵的所有行和列都为0,因此也可以说不可分割的网络模块度为0。利用[math]\displaystyle{ sv = ±1 }[/math]代表节点[math]\displaystyle{ v }[/math]所属于哪个节点组,我们有:
- [math]\displaystyle{ Q = {1\over 4m} \sum_{vw} B_{vw} s_v s_w = {1\over 4m} \mathbf{s}^\mathrm{T}\mathbf{Bs} }[/math]
其中,[math]\displaystyle{ s }[/math]为包含</math>s_v</math>的列向量。
该函数与辛流形的汉密尔顿函数 Hamiltonian的形式相同,故可创建出简单的算法,例如使用模拟退火算法 Simulated Annealing来使模块度最大化。 模块化的一般形式等价于一个 Potts 自旋玻璃,在这种情况下也可以发展类似的算法。
多社团检测实例
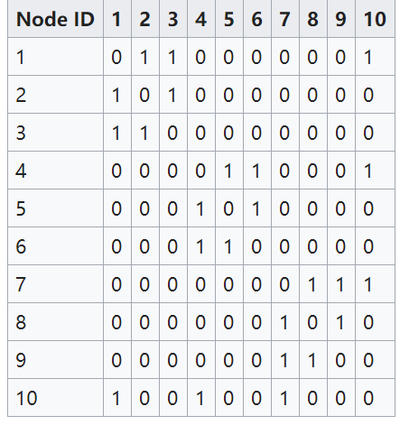
我们考虑一个有10个节点和12条边的无向网络,下面是邻接矩阵 Adjacency Matrix。
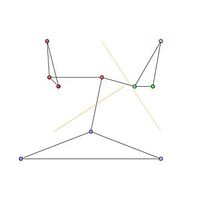
图中的社团由图1中的红色、绿色和蓝色节点簇表示。最佳社团划分如图2所示。
多分辨率算法
在利用模块度衡量社团划分质量的过程中,有两种主要的解决分辨率限制的方法: 在每个节点上以自循环的形式增加一个阻力 r,通过增加或减少坏节点形成社团; 或在模块化定义的空格项前加上一个参数γ>0,该参数控制社区内部链接与零模型之间的相对重要性。 将这些参数值的模块度优化到适当的范围内,就有可能恢复整个网络的中尺度,从宏观尺度上所有节点属于同一个社团,从微观尺度上每个节点都形成自己的社团,因而将其命名为多分辨率算法。 然而,当社团之间的规模差异很大时,这些算法也有局限性。
分辨率限制
将一个给定网络与该网络相对应的随机零模型进行对比,随机模型通常具有相同度序列、且其连边随机连接。模块度通过比较社团内部的连边数量与所期望的连边数量来判断给定网络是否具有较强的社团结构。(参见:网络科学导论。)这个随机零模型隐含地假设每个节点可以连接到网络的任何其他节点。 然而,如果网络规模非常大,这种假设是不合理的。因为通过一个节点的视角看到了网络的一小部分,却忽略了网络的大部分。 这说明随着网络规模的增大,两组节点之间的期望边数会减少。 因此,如果网络足够大,模块化零模型中两组节点集之间的期望边数可能小于一条。 在该种情况下,模块度将两组节点集之间存在单边作为节点集之间强相关性的标志。若对模块度进行优化,将导致两组节点集的合并,独立于社团群众。 因此,即使是内部连边密度最高、可识别性最好的弱互联完全图,在网络规模足够大的情况下,也可以通过模块度优化进行合并。 因此,即使小型社团能够被准确定义,在大型网络中优化模块度的方法也并不适用于他们。 对于依赖全局零模型的模块度优化方法来说,这种偏差是不可避免的。
模块度最大化算法
由于网络所有可能的社团划分方法十分多,假设网络的节点数和边数分别为n和m,则所有可能的社团划分数是一个以n为指数的数。因此,NP-hard问题被提出,其研究如何在所有可能的划分中找出最优划分。针对这一问题,目前一些相应算法已被提出,其可以在合理的时间内找出模块度最大化的近似最优划分。
经典贪婪算法
模块度最大化问题是一个经典的最优化问题,马克·纽曼 Mark NewMan 基于贪婪思想提出了模块度最大化的贪婪算法 Fast NewMan(FN) 。贪婪思想的目标是找出目标函数的整体最优值或者近似最优值,它将整体最优化问题分解为局部最优化问题。找出每个局部最优值,最终将局部最优值整合成整体的近似最优值。初始时,FN算法将网络中的每个节点都看成独立的小社团。然后考虑所有相连社区两两合并的情况,计算每种合并带来的模块度的增量。基于贪婪原则,选取使模块度增长最大或者减小最少的两个社团,将它们合并成一个社团。如此循环迭代,直到所有结点合并成一个社区。随着迭代的进行,网络总的模块度是不断变化的,在模块度的整个变化过程中,其最大值对应网络的社团划分就视为最优社团划分。 贪婪算法FN具体步骤:
- 去掉网络中所有的边,网络的每个节点都单独作为一个社团;
- 网络中的每个连通部分作为一个社团,将还未加入网络的边分别重新加回网络,每次加入一条边,如果加入网络的边连接了两个不同的社团,则合并两个社团,并计算形成新社团划分的模块度增量。选择使模块度增量最大或者减小最少的两个社区进行合并。
- 如果网络的社区数大于1,则返回步骤 2,继续迭代,否则转到步骤 4;
- 遍历每种社区划分对应的模块度值,选取模块度最大的社区划分作为网络的最优划分。
该算法中,需要注意的是,每次加入的边只是影响网络的社团划分。而每次计算网络划分的模块度时,都是在网络完整的拓扑结构上进行的,即网络所有的边都存在的拓扑结构上。
快速模块度优化算法
为了降低算法的时间复杂度,文森特·布隆代尔 Vincent Blondel等人提出了另一种层次贪婪算法,名为Louvain modularity。该算法包括两个阶段,第一阶段合并社团,算法将每个节点当作一个社团,基于模块度增量最大化标准决定哪些相邻的社团应该被合并。经过一轮扫描后开始第二阶段,算法将第一阶段发现的所有社团重新看成节点,构建新的网络,在新网络上重复进行第一阶段,这两个阶段重复运行,直到网络社团划分的模块度不再增长,得到网络的社团近似最优划分。 这个简单算法具有以下几个优点:
- 该算法的步骤比较直观并且易于实现;
- 不需要提前设定网络的社团数,并且该算法可以呈现网络的完整的分层社团结构,能够发现在线社交网络的分层虚拟社区结构,获得不同分辨率的虚拟社区;
- 计算机模拟实验显示:在稀疏网络上,该算法在合理的时间内可以处理结点数超过10^9的网络,因此十分适合在线社交网络这样超大规模的网络中检测最优的社团划分。
进一步阅读
编者推荐
文献推荐
网络中群落结构的发现和分析是近年来物理学界非常关注的一个课题,但由于计算量大,目前提出的大多数方法都不适合大型网络。这篇文章提出了一种新的聚类算法来检测群落结构,它比很多同类型的算法收敛地更快。作为这个算法应用的一个例子,这篇文章使用它来分析一个大型在线零售商网站上的销售项目网络,如果这些项目经常被同一个买家购买,那么网络中的项目就会被连接。该网络有超过40万个顶点和200万条边,该算法可以从这个网络中提取出有意义的社区,揭示了顾客购买习惯中存在的大规模模式。
这篇文章提出并研究了一种在网络节点自然划分为子群时发现社团结构的算法,同时提出了一个度量算法发现的社团结构的强度的方法。
这篇文章论证了模块度可以用特征矩阵的特征向量来表示网络(称之为“模块性矩阵”),且在较短的运行时间,通过特征向量的社团检测算法返回的结果质量明显高于同类算法,并通过数据集的应用程序来说明这个方法。
基于模块度的社团检测包含许多被广泛使用的、有效的启发式方法来识别单层和多层网络中的结构。最近,一种用于模块度优化的传播方法为非平凡结构的识别提供了一种有用的指导,而其他优化方法则没有这种方法,这篇文章将模块度传播扩展到多层网络中。
集智文章推荐
近期,一个由北京师范大学、中国科学院、美国波士顿大学、以色列巴伊兰大学多位学者组成的研究团队,在Nature Communications上发表文章,以1893年至2010年间发表在美国物理学会(APS)期刊上的482566篇为例,通过书目耦合方法建立共引网络,描述了科学家文章之间的关系,并运用社团结构分析的方法将不同的研究兴趣具体化,进一步研究了科学家兴趣转移的趋势及动力学问题,提出了一个能解释科研兴趣转移机制主要特征的开发-探索模型。
这篇文章的重点是网络科学家的合著网络,两个科学家共同发表过至少一篇论文,他们之间就形成了合著关系。在此之前,只有Newman的团队分析过网络科学家的合著关系网络,但他们当时网络只包含1589位科学家,而这篇文章的研究涵盖了20年内的52406位科学家以及329181个合著关系。
本中文词条由趣木木用户参与编译,苏格兰用户审校,乐多多编辑,欢迎在讨论页面留言
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。