双重差分
双重差分法 Difference in differences(DID[1] 或 DD[2])是一种用于计量经济学和社会科学定量研究的统计技术,它试图利用观察性研究数据来模拟实验研究设计,通过研究自然实验[3]中的“治疗组”和“对照组”之间的差异性效果。它通过比较治疗组和对照组的结果变量在一段时间的平均变化,计算出治疗(即解释变量或自变量)对结果(即反应变量或因变量)的影响。虽然该方法旨在减轻外部因素和选择偏差的影响,但取决于治疗组的选择方式,该方法仍可能受到某些偏差的影响(例如,均值回归、反向因果关系和遗漏变量偏差)。
与受试者治疗效果的时间序列估计(分析随时间变化的差异)或治疗效果的横截面估计(衡量治疗组和对照组之间的差异)不同,双重差分法使用面板数据来衡量治疗组和对照组的结果变量随时间变化的差异。
一般定义
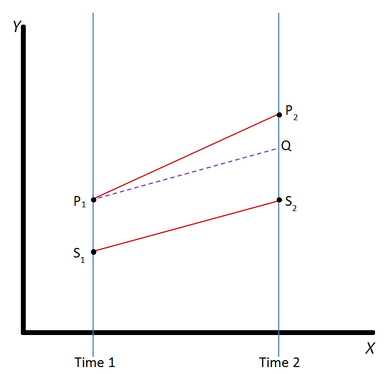
双重差分法要求从治疗组和对照组在两个或两个以上不同时间段测量数据,特别是“治疗”前以及“治疗”后的至少一个时间段。在图中的示例中,治疗组的结果用线P表示,对照组的结果用线S表示。两组的结果(因)变量都是在时间1,即任何一组接受治疗(即自变量或解释变量)前测量的,分别由点P1和S1表示。治疗组之后接受或经历治疗,并在时间2再次测量两组。并非所有治疗组和对照组在时间2的差异(即P2和S2的差异)都可以解释为是治疗的效果,因为治疗组和对照组在时间1的开始时间不同。因此,DID计算出两组的结果变量之间的“正常”差异(如果两组均未接受治疗,差异仍然存在),由虚线Q表示(注意:P1到Q的斜率与S1到S2的斜率相同)。治疗效果是观察结果(P2)和“正常”结果(P2和Q之间的差异)之间的差异。
正式定义
考虑以下模型
- [math]\displaystyle{ y_{it} ~=~ \gamma_{s(i)} + \lambda_t + \delta I(\dots) + \varepsilon_{it} }[/math]
其中, [math]\displaystyle{ y_{it} }[/math]是个体[math]\displaystyle{ i }[/math]和时间[math]\displaystyle{ t }[/math]的因变量,[math]\displaystyle{ s(i) }[/math]是[math]\displaystyle{ i }[/math]所属的组(即治疗组或对照组) 。 [math]\displaystyle{ I(\dots) }[/math]则是哑变量的简称,当[math]\displaystyle{ (\dots) }[/math]中所描述的事件为真时等于1,否则等于0。在时间与[math]\displaystyle{ Y }[/math]的分组图中,[math]\displaystyle{ \gamma_s }[/math]是[math]\displaystyle{ s }[/math]组的图形的垂直截距,而[math]\displaystyle{ \lambda_t }[/math]是根据平行趋势假设,两组共享的时间趋势(见下文假设)。[math]\displaystyle{ \delta }[/math]是治疗效果,[math]\displaystyle{ \varepsilon_{it} }[/math]是残差项。
考虑按组和时间划分的因变量和虚拟指标的平均值:
- [math]\displaystyle{ \begin{align} n_s & = \text{ number of individuals in group } s \\ \overline{y}_{st} & = \frac{1}{n_s} \sum_{i=1}^n y_{it} \ I(s(i) ~=~ s), \\ \overline{\gamma}_s & = \frac{1}{n_s} \sum_{i=1}^n \gamma_{s(i)} \ I(s(i) ~=~ s) ~=~ \gamma_s, \\ \overline{\lambda}_{st} & = \frac{1}{n_s} \sum_{i=1}^n \lambda_t \ I(s(i) ~=~ s) ~=~ \lambda_t, \\ D_{st} & = \frac{1}{n_s} \sum_{i=1}^n I(s(i) ~=~\text{ treatment, } t \text{ in after period}) \ I(s(i) ~=~ s) ~=~ I(s ~=~\text{ treatment, } t \text{ in after period}) , \\ \overline{\varepsilon}_{st} & = \frac{1}{n_s} \sum_{i=1}^n \varepsilon_{it} \ I(s(i) ~=~ s), \end{align} }[/math]
为简单起见,假设 [math]\displaystyle{ s=1,2 }[/math],[math]\displaystyle{ t=1,2 }[/math]。请注意, [math]\displaystyle{ D_{st} }[/math]不是随机的,它只是编码了组和时期的标记方式。那么
- [math]\displaystyle{ \begin{align} & (\overline{y}_{11} - \overline{y}_{12}) - (\overline{y}_{21} - \overline{y}_{22}) \\[6pt] = {} & \big[ (\gamma_1 + \lambda_1 + \delta D_{11} + \overline{\varepsilon}_{11}) - (\gamma_1 + \lambda_2 + \delta D_{12} + \overline{\varepsilon}_{12}) \big] \\ & \qquad {} - \big[ (\gamma_2 + \lambda_1 + \delta D_{21} + \overline{\varepsilon}_{21}) - (\gamma_2 + \lambda_2 + \delta D_{22} + \overline{\varepsilon}_{22}) \big] \\[6pt] = {} & \delta (D_{11} - D_{12}) + \delta(D_{22} - D_{21}) + \overline{\varepsilon}_{11} - \overline{\varepsilon}_{12} + \overline{\varepsilon}_{22} - \overline{\varepsilon}_{21}. \end{align} }[/math]
严格外生性假设 Strict exogeneity assumption则意味着
- [math]\displaystyle{ \operatorname{E} \left [ (\overline{y}_{11} - \overline{y}_{12}) - (\overline{y}_{21} - \overline{y}_{22}) \right ] ~=~ \delta (D_{11} - D_{12}) + \delta(D_{22} - D_{21}). }[/math]
在不失一般性的前提下,假设[math]\displaystyle{ s = 2 }[/math]是治疗组,[math]\displaystyle{ t = 2 }[/math]是后一期,则[math]\displaystyle{ D_{22}=1 }[/math] and [math]\displaystyle{ D_{11}=D_{12}=D_{21}=0 }[/math],得到 DID 估计量
- [math]\displaystyle{ \hat{\delta} ~=~ (\overline{y}_{11} - \overline{y}_{12}) - (\overline{y}_{21} - \overline{y}_{22}), }[/math]
这可以解释为[math]\displaystyle{ D_{st} }[/math]所示的治疗效果。下面展示了如何将这个估计值解读为普通最小二乘回归中的系数。本节描述的模型是过度参数化的; 为了弥补这一点,可以将哑变量的一个系数设置为0,例如,我们可以设置[math]\displaystyle{ \gamma_1 = 0 }[/math]。
假设
普通最小二乘法 Ordinary least squares(OLS)模型的所有假设同样适用于DID。此外,使用DID方法还需要满足平行趋势假设。平行趋势假设认为在[math]\displaystyle{ s=1 }[/math]和[math]\displaystyle{ s=2 }[/math]中 [math]\displaystyle{ \lambda_2 - \lambda_1 }[/math]的值都是相同的。鉴于上面的正式定义准确地代表了现实,这个假设自动成立。然而,符合[math]\displaystyle{ \lambda_{st} ~:~ \lambda_{22} - \lambda_{21} \neq \lambda_{12} - \lambda_{11} }[/math]的模型可能更加符合现实。为了增加平行趋势假设成立的可能性,双重差分法往往与匹配法[4]相结合。这就涉及将已知的“治疗”单元与模拟的反事实“控制”单元进行“匹配”: 即得到未接受治疗的特征等效单元。通过将结果变量定义为时间差异(治疗前后的观察结果的变化) ,并根据类似的治疗前历史对大样本中的多个单元进行匹配,所得出的ATE结果(即ATT:受治疗者的平均治疗效果)提供了一个稳健的治疗效果差异估计。这样做有两个统计学目的:首先,以治疗前协变量为条件,平行趋势假设很可能成立; 其次,这种方法减少了对有效推论所必需的相关可忽略性假设的依赖。
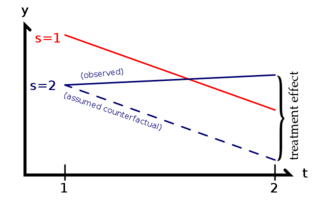
如右图所示,治疗效果是观察到的y值与未治疗的情况下y值的平行趋势之间的差异。DID的致命缺点是当一组中治疗以外的某些因素发生了变化,而另一组在治疗的同时没有变化,这意味着违反了平行趋势假设。
为了保证DID估计的准确性,假定两组个体的组成在一段时间内保持不变。在使用 DID 模型时,必须考虑和处理可能影响结果的各种问题,如自相关[5]和 Ashenfelter 倾斜。
实现
DID 方法可以根据下表实现,其中右下角的单元格是 DID 估计器。
| [math]\displaystyle{ y_{st} }[/math] | [math]\displaystyle{ s=2 }[/math] | [math]\displaystyle{ s=1 }[/math] | Difference |
|---|---|---|---|
| [math]\displaystyle{ t=2 }[/math] | [math]\displaystyle{ y_{22} }[/math] | [math]\displaystyle{ y_{12} }[/math] | [math]\displaystyle{ y_{12}-y_{22} }[/math] |
| [math]\displaystyle{ t=1 }[/math] | [math]\displaystyle{ y_{21} }[/math] | [math]\displaystyle{ y_{11} }[/math] | [math]\displaystyle{ y_{11}-y_{21} }[/math] |
| Change | [math]\displaystyle{ y_{21}-y_{22} }[/math] | [math]\displaystyle{ y_{11}-y_{12} }[/math] | [math]\displaystyle{ (y_{11}-y_{21})-(y_{12}-y_{22}) }[/math] |
运行回归分析也会得到相同的结果。考虑 OLS 模型
- [math]\displaystyle{ y ~=~ \beta_0 + \beta_1 T + \beta_2 S + \beta_3 (T \cdot S) + \varepsilon }[/math]
其中[math]\displaystyle{ T }[/math]是表示时期的哑变量,当[math]\displaystyle{ t=2 }[/math]时[math]\displaystyle{ T=1 }[/math];[math]\displaystyle{ S }[/math]是表示群体成员的哑变量,当[math]\displaystyle{ s=2 }[/math]时[math]\displaystyle{ S=1 }[/math]。综合变量[math]\displaystyle{ (T \cdot S) }[/math]是一个哑变量,表示当[math]\displaystyle{ S=T=1 }[/math]时的情况。虽然这里没有严格说明,但这是模型形式定义的适当参数化。此外,该部分中的组和周期平均值与模型参数估计有关,如下所示
- [math]\displaystyle{ \begin{align} \hat{\beta}_0 & = \widehat{E}(y \mid T=0,~ S=0) \\[8pt] \hat{\beta}_1 & = \widehat{E}(y \mid T=1,~ S=0) - \widehat{E}(y \mid T=0,~ S=0) \\[8pt] \hat{\beta}_2 & = \widehat{E}(y \mid T=0,~ S=1) - \widehat{E}(y \mid T=0,~ S=0) \\[8pt] \hat{\beta}_3 & = \big[\widehat{E}(y \mid T=1,~ S=1) - \widehat{E}(y \mid T=0,~ S=1)\big] \\ & \qquad {} - \big[\widehat{E}(y \mid T=1,~ S=0) - \widehat{E}(y \mid T=0,~ S=0)\big], \end{align} }[/math]
其中[math]\displaystyle{ \widehat{E}(\dots \mid \dots ) }[/math]代表在样本上计算的条件平均值,例如,[math]\displaystyle{ T=1 }[/math] 是后时期的指标, [math]\displaystyle{ S=0 }[/math]是对照组的指标。请注意,[math]\displaystyle{ \hat{\beta}_1 }[/math] 是对反事实的估计,而不是对照组的影响。对照经常被用作反事实的替代(见合成控制方法,以便更深入地理解这一点)。因此,[math]\displaystyle{ \hat{\beta}_1 }[/math]可以被解释为对照组和干预(治疗)的反事实的影响。同样,由于平行趋势假设,[math]\displaystyle{ T=1 }[/math]时,治疗组和对照组之间也存在相同的差异,即[math]\displaystyle{ \hat{\beta}_2 }[/math]。上述描述不应该被解释为仅是对照组对\hat{\beta}_1的(平均)效应,或者仅仅是治疗组和对照组在前期的差异,[math]\displaystyle{ \hat{\beta}_2 }[/math]。正如 Card 和 Krueger 所说,结果变量的一阶差分([math]\displaystyle{ (\Delta Y_i = Y_{i,1} - Y_{i,0}) }[/math])消除了对时间趋势(即[math]\displaystyle{ \hat{\beta}_1 }[/math])形成无偏估计的需要([math]\displaystyle{ \hat{\beta}_3 }[/math]),这意味着[math]\displaystyle{ \hat{\beta}_1 }[/math]实际上并不取决于治疗组或对照组[6]。一致地,治疗组和对照组之间的差异将消除治疗差异(即,[math]\displaystyle{ \hat{\beta}_2 }[/math])的需要,进而形成对[math]\displaystyle{ \hat{\beta}_3 }[/math]的无偏估计。这种细微差别对于了解用户何时认为(微弱)违反平行预趋势或在存在非共同冲击或混杂事件的情况下违反适当的反事实近似假设是非常重要的。为了看清该符号与前面章节之间的关系,如上所述,考虑小组每个时间段只有一个观察值,那么
- [math]\displaystyle{ \begin{align} \widehat{E}(y \mid T=1,~ S=0) & = \widehat{E}(y \mid \text{ after period, control}) \\ [3pt] \\ & = \frac{ \widehat{E}(y \ I(\text{ after period, control}) )}{ \widehat{P}(\text{ after period, control})} \\ [3pt] \\ & = \frac{ \sum_{i=1}^n y_{i,\text{after}} I(i \text{ in control}) } { n_{\text{control}} } = \overline{y}_{\text{control, after}} \\ [3pt] \\ & = \overline{y}_{\text{12}} \end{align} }[/math]
等等,对于[math]\displaystyle{ T }[/math]和[math]\displaystyle{ S }[/math]的其他值,这相当于
- [math]\displaystyle{ \hat{\beta}_3 ~=~ (y_{11} - y_{21}) - (y_{12} - y_{22}). }[/math]
但这是正式定义和上表中给出的治疗效果的表达式。
Card和Krueger (1994)的研究示例
关于DID,最著名的研究之一便是 Card 和 Krueger 在1994[7]年发表的关于新泽西州最低工资的文章。Card 和 Krueger 比较了1992年2月和1992年11月新泽西州最低工资从4.25美元上升到5.05美元之后,新泽西州和宾夕法尼亚州快餐部门的就业情况。仅在治疗前后观察新泽西州的就业情况变化,将无法控制一些被忽略变量,例如该地区的天气和宏观经济状况。通过将宾夕法尼亚州作为双重差分模型的对照,任何由新泽西州和宾夕法尼亚州的共同变量所引起的偏差都会被隐含的控制,即使这些变量是不可被观测到的。假设新泽西州和宾夕法尼亚州随着时间的推移有平行的趋势,那么宾夕法尼亚州的就业变化就可以解释为新泽西州在没有提高最低工资的情况下,会产生的变化,反之亦然。证据表明,提高最低工资并没有导致新泽西州就业率的下降,这与一些经济理论的说法恰恰相反。下表显示了 Card 和 Krueger 对就业治疗效果的估计,以 FTEs (或全职人力工时)衡量。Card 和 Krueger 估计,新泽西州0.80美元的最低工资增长导致了2.75个全职雇员的就业增加。
| 新泽西州 | 宾夕法尼亚州 | 差异 | |
|---|---|---|---|
| 二月 | 20.44 | 23.33 | −2.89 |
| 十一月 | 21.03 | 21.17 | −0.14 |
| 变化 | 0.59 | −2.16 | 2.75 |
另见
参考文献
- ↑ Abadie, A. (2005). "Semiparametric difference-in-differences estimators". Review of Economic Studies. 72 (1): 1–19. CiteSeerX 10.1.1.470.1475. doi:10.1111/0034-6527.00321.
- ↑ Bertrand, M.; Duflo, E.; Mullainathan, S. (2004). "How Much Should We Trust Differences-in-Differences Estimates?" (PDF). Quarterly Journal of Economics. 119 (1): 249–275. doi:10.1162/003355304772839588.
- ↑ Angrist, J. D.; Pischke, J. S. (2008). Mostly Harmless Econometrics: An Empiricist's Companion. Princeton University Press. pp. 227–243. ISBN 978-0-691-12034-8. https://books.google.com/books?id=ztXL21Xd8v8C&pg=PA227.
- ↑ Basu, Pallavi; Small, Dylan (2020). "Constructing a More Closely Matched Control Group in a Difference-in-Differences Analysis: Its Effect on History Interacting with Group Bias" (PDF). Observational Studies. 6: 103–130.
- ↑ Bertrand, Marianne; Duflo, Esther; Mullainathan, Sendhil (2004). "How Much Should We Trust Differences-In-Differences Estimates?" (PDF). Quarterly Journal of Economics. 119 (1): 249–275. doi:10.1162/003355304772839588.
- ↑ Card, David; Krueger, Alan B. (1994). "Minimum Wages and Employment: A Case Study of the Fast-Food Industry in New Jersey and Pennsylvania". American Economic Review. 84 (4): 772–793. JSTOR 2118030.
- ↑ Card, David; Krueger, Alan B. (1994). "Minimum Wages and Employment: A Case Study of the Fast-Food Industry in New Jersey and Pennsylvania". American Economic Review. 84 (4): 772–793. JSTOR 2118030.
进一步阅读
- Angrist, J. D.; Pischke, J. S. (2008). Mostly Harmless Econometrics: An Empiricist's Companion. Princeton University Press. pp. 227–243. ISBN 978-0-691-12034-8. https://books.google.com/books?id=ztXL21Xd8v8C&pg=PA227.
- Cameron, Arthur C.; Trivedi, Pravin K. (2005). Microeconometrics: Methods and Applications. Cambridge university press. pp. 768–772. doi:10.1017/CBO9780511811241. ISBN 9780521848053. https://api.semanticscholar.org/CorpusID:120313863.
- Imbens, Guido W.; Wooldridge, Jeffrey M. (2009). "Recent Developments in the Econometrics of Program Evaluation". Journal of Economic Literature. 47 (1): 5–86. doi:10.1257/jel.47.1.5.
- Bakija, Jon; Heim, Bradley (August 2008). "How Does Charitable Giving Respond to Incentives and Income? Dynamic Panel Estimates Accounting for Predictable Changes in Taxation". NBER Working Paper No. 14237. doi:10.3386/w14237.
- Conley, T.; Taber, C. (July 2005). "Inference with 'Difference in Differences' with a Small Number of Policy Changes". NBER Technical Working Paper No. 312. doi:10.3386/t0312.
外部链接
- 差异估计差异,医疗经济学家网站
编者推荐
集智课程
因果科学读书会第三季:因果+X
“因果”并不是一个新概念,而是一个已经在多个学科中使用了数十年的分析技术。通过前两季的分享,我们主要梳理了因果科学在计算机领域的前沿进展。如要融会贯通,我们需要回顾数十年来在社会学、经济学、医学、生物学等多个领域中,都是使用了什么样的因果模型、以什么样的范式、解决了什么样的问题。我们还要尝试进行对比和创新,看能否以现在的眼光,用其他的模型,为这些研究提供新的解决思路。
“因果+X”就是要让因果真正地应用于我们的科学研究中,不管你是来自计算机、数理统计领域,还是社会学、经济学、管理学领域,还是医学、生物学领域,我们希望共同探究出因果研究的范式,真正解决因果的多学科应用问题,乃至解决工业界的问题。
计算社会经济学的内容与方法
准确和及时的感知社会经济发展状态,对理解社会结构演化和制定经济发展策略非常重要。近年来,私营部门积累的大规模数据,以低获取成本、实时更新和高时空分辨率等优势,弥补了传统经济普查的不足。统计机器学习算法的飞速发展,也极大的提高了对未来发展态势的准确预测。作为新数据和新方法催生的一门交叉学科,计算社会经济学将有机会更好的回答一些新的社会经济问题,比如:从在线社会网络的结构中,能不能推断出一个人的财富状况?除了翻阅统计年鉴,怎样快速的感知陌生城市的社会经济状态?在国家和区域的经济发展中,有没有最优的产业升级路径和策略?
该课程中,电子科技大学博士生高见,将系统性的介绍计算社会经济学的主要研究内容和分析方法,阐述大规模社会经济数据(包括卫星遥感数据、手机通讯数据、社交媒体数据等)在解决全球贫困问题、刻画区域经济结构、推断个体财富和应急抢险救灾中的具体应用。
本中文词条由小猴子翻译,薄荷编辑,如有问题,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。