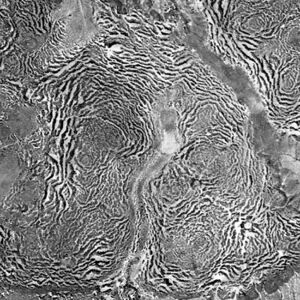
斑图生成

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
跳到导航 跳到搜索


树突生长计算模型中的模式形成。

概述

斑图（或称模式）即复杂系统中个体状态的组合形成的一些更大尺度的集体结构。斑图可以是时间或空间上的，波纹、斑点、分形、对称等都是斑图。斑图是自组织形成的，其涌现与演化过程和对称性破缺有关。

斑图生成学关注自组织中可见的、统计有序的结果，以及自然界中相似斑图背后的共同原理。


在发育生物学 Developmental Biology中，斑图生成指的是细胞命运中复杂组织的产生过程。斑图生成由基因控制的。基因在斑图生成中所起的作用属于形态发生的一个方面，即由相似的基因演化出不同的生命结构，当下也属于演化发育生物学所探究的问题。模式生物黑腹果蝇（第一个应用到形态发生研究的物种）的胚胎的斑图生成过程和蝴蝶的眼点清楚地体现了这一机制，而后者的发育过程是标准（果蝇）机制的一种变体。


实例

在生物、化学、物理和数学 [1] 中都有斑图生成的实例，并且我们可以用计算机图形学 Computer Graphics轻松地来模拟，下面依次进行介绍。


生物学

动物标记、动物分节和叶序等生物学斑图是以不同的方式形成的。[2]


在发育生物学中，斑图生成描述了胚胎组织发育中最初相同的细胞逐步呈现出复杂形态和功能的机制。[3] 以果蝇为例，胚胎发育 Embryogenesis涉及到细胞命运的协调控制。[4][5][6]斑图生成是由遗传基因所控制，通常涉及一个场中的每个细胞沿着形态发生素梯度感知和响应其位置，然后通过细胞信号通路进行短距离的细胞间通信以完善初始斑图。在此背景下，细胞场 A Field of Cells是指通过响应同一组位置信息线索而影响其细胞命运的一组细胞。这个概念模型最早在20世纪60年代被描述为法旗模型 French Flag Model。[7][8]更一般来说，生物体的形态是由进化发育生物学 Evolutionary Developmental Biology的机制，如改变胚胎中特定发育事件的时间和位置所决定的。[9]


生物系统中可能存在的斑图生成机制包括：阿兰 · 图灵 Alan Turing[10]提出的经典反应—扩散 Reaction–Diffusion模型和最近发现的弹性不稳定机制，后者被认为是高等动物大脑皮层上褶皱模式等形成的原因。[11][12]


菌落生长

细菌菌落在生长过程中形成的斑图种类繁多，其形状取决于生长环境。特别是包括培养基环境的严酷程度、营养物质的缺乏等在内的各种外部压力，会增强了所产生斑图的复杂性。[13] 对于其他生物，如粘液霉菌，则显示出由化学信号动力学驱动的非同寻常的斑图。[14]细胞体现（延伸和粘附）也会对发育模式产生影响。[15]


植被斑图

虎皮纹灌木是一种在干旱条件下形成的植被模式。

虎皮纹灌木[16] 和冷杉波纹[17]等植被斑图形成的原因不同。在尼日尔等干旱国家，植物生长受到降雨的限制，虎皮纹灌木由干旱斜坡上的带状灌木组成。每一条大致水平的植被带都可以从紧靠其上方的裸露地带吸收雨水。[16] 相比之下，在受到大风摧残后的植被再生过程中，山坡上的森林会出现冷杉波纹。当较外层树木倒下时，曾经受到它们庇护的内层树木会暴露在外，进而这部分植被更容易受到破坏。因此，树林空隙往往向背风面扩大。同时在迎风坡，幼树在生长过程中则受到存活下来的高大树木自然形成的风影区保护。[17] 因此在平坦的地形中，植被除了条带状之外，还出现了其他的斑图形态—例如六边形缝隙斑图和六边形点状斑图。在这种情况下，植被斑图是在当地植被生长和朝向生长位置的水分输送之间的正反馈回路驱动下形成的。[18][19].


化学

在化学和化学工程领域，斑图生成的研究进展良好，其中包括温度和浓度斑图。[20]由伊利亚·普利高津 Ilya Prigogine和其合作者开发的布鲁塞尔器 Brusselator模型就是一个展示出图灵不稳定性 Turing Instability的例子。[21]化学体系中的斑图生成通常涉及振荡化学动力学 Oscillatory Chemical Kinetics或自催化反应 Autocatalytic Reactions，[22]如别洛乌索夫-扎波茨基反应 Belousov–Zhabotinsky Reaction或布里格斯-劳舍反应 Briggs–Rauscher Reaction。在工业应用中，如化学反应堆，斑图生成可能导致温度热点，进而会降低产量或造成灾害性安全问题，如热失控。[23][20] 斑图生成的出现可以用底层的反应—扩散系统的数学建模与模拟来研究。[20][22]

  • 别洛乌索夫-扎波茨基反应（BZ反应）是一类作为非平衡热力学经典例子的反应，会促成非线性化学振荡器的建立。（这些振子中唯一共同的元素是溴和酸。）这类反应对于理论化学很重要，因为它们表明化学反应不必受平衡热力学行为的支配。这些反应远未达到平衡，并在相当长的一段时间内保持非平衡状态，并无序地发展。从这个意义上说，它们为非平衡的生物学现象（需要澄清？）提供了一个有价值的化学模型；因此，BZ反应本身的数学模型和模拟具有理论意义，揭示某类现象作为噪声驱动的秩序的性质。


BZ反应的一个本质内容就是所谓的“可激发性”；在刺激因素的影响下，斑图可以在原本完全静止的介质中形成。一些时钟反应，如Briggs-Rauscher和BZ，使用三（联吡啶）氯化钌作为催化剂，可以在光的影响下激发产生自组织活动。


物理学

20世纪80年代，卢贾托 Lugiato和勒弗 Lefever开发了一个光在光学谐振腔中传播的模型，该模型通过利用非线性效应形成斑图。


如伯纳德涡流 Bénard Cells、激光、条状云或卷状云、冰柱上的涟漪、泥路上的洗衣板等图案以及凝固中的树突、液晶，孤子 Solitons等。


瑞利-伯纳德对流是一种自然对流，当从下方加热流体时，出现在流体表面水平层中，其中流体会产生一种形似细胞的规则对流斑图，称为伯纳德涡流。由于无论是进行理论分析还是实验研究都很方便，瑞利-伯纳德对流是研究最广泛的对流现象之一。这一对流斑图是自组织非线性系统中研究最透彻的一例。


浮力和重力的影响是对流细胞斑图出现的原因。最初的运动是密度较小的流体从受热的底层上涌。这种上升流自发地组织成一种规则的细胞斑图。


在数学和物理学中，孤子或孤立波是一种自我增强的波包，在以恒定速度传播时保持其形状。孤子是由于介质中非线性和色散效应的抵消而产生的。（色散效应是某些系统的一种特性，在这种系统中，波的速度取决于它的频率。）孤子是描述物理系统的一类广泛存在的弱非线性色散偏微分方程的解。


1834年，约翰·斯科特·罗素 John Scott Russell（1808-1882）在苏格兰联合运河观测到一个孤波，首次描述了孤波现象。之后他在一个波浪槽中再现了这一现象，并将其命名为“转化波”。


数学

例如最密堆积（球填充）和覆盖。数学是其他斑图生成机制的基础。


在几何学中，球填充是在一个包含空间内不重叠的球的排列。球通常都具有相同的尺寸，填充空间一般指三维的欧几里得空间。然而，球填充问题可以推广到不相等的球、其他维度的空间（二维的问题变成圆填充，高维的问题变成超球填充）或非欧几里得空间，如双曲空间。


一个典型的球填充问题是找到一种安排，在其中球填充尽可能多的空间。球体所占空间的比例称为排列密度。由于在无限空间中填充的局部密度可能随测量的体积而变化，因此问题通常是使在足够大的体积上测量的平均密度或渐近密度最大化。


对于三维尺寸相等的球体，最密的填充使用大约74%的体积。随机排列的等量球体的密度通常在64%左右。


计算机图形学

利用图像锐化和虚化产生的斑图近似反应-扩散模型。

一些类型的自动机已经用来生成类似有机外观的纹理，为三维物体提供更真实的阴影效果。[24][25]


KPT6是流行的Photoshop插件，包一个名为“KPT反应”的过滤器。反应该根据提供的种子图像产生反应-扩散风格的图案。


在数字图像处理中，只要有一点耐心，通过在图形编辑器中反复锐化和模糊图像，就可以用卷积函数实现类似于“KPT反应”的效果。如果使用其他滤波器，如浮雕或边缘检测，可以实现不同类型的效果。


计算机经常被用来模拟导致斑图生成的生物、物理或化学过程，它们可以以逼真的方式显示结果。使用反应—扩散或MClone等模型的计算是基于科学家们为模拟研究现象而设计的实际数学方程。

参考文献

  1. ↑ Ball, 2009.
  2. ↑ Ball, 2009. Shapes, pp. 231–252.
  3. ↑ Ball, 2009. Shapes, pp. 261–290.
  4. ↑ Eric C. Lai (March 2004). "Notch signaling: control of cell communication and cell fate". Development. 131 (5): 965–73. doi:10.1242/dev.01074. PMID 14973298.
  5. ↑ Melinda J. Tyler, David A. Cameron (2007). "Cellular pattern formation during retinal regeneration: A role for homotypic control of cell fate acquisition". Vision Research. 47 (4): 501–511. doi:10.1016/j.visres.2006.08.025. PMID 17034830.{{cite journal}}: CS1 maint: uses authors parameter (link)
  6. ↑ Hans Meinhard (2001-10-26). "Biological pattern formation: How cell[s] talk with each other to achieve reproducible pattern formation". Max-Planck-Institut für Entwicklungsbiologie, Tübingen, Germany.
  7. ↑ Wolpert L (October 1969). "Positional information and the spatial pattern of cellular differentiation". J. Theor. Biol. 25 (1): 1–47. doi:10.1016/S0022-5193(69)80016-0. PMID 4390734.
  8. ↑ Wolpert, Lewis (2007). Principles of development (3rd ed.). Oxford [Oxfordshire]: Oxford University Press. ISBN 978-0-19-927536-6. 
  9. ↑ Hall, B. K. (2003). "Evo-Devo: evolutionary developmental mechanisms". International Journal of Developmental Biology. 47 (7–8): 491–495. PMID 14756324.
  10. ↑ S. Kondo, T. Miura, "Reaction-Diffusion Model as a Framework for Understanding Biological Pattern Formation", Science 24 Sep 2010: Vol. 329, Issue 5999, pp. 1616-1620 DOI: 10.1126/science.1179047
  11. ↑ Mercker, M; Brinkmann, F; Marciniak-Czochra, A; Richter, T (4 May 2016). "Beyond Turing: mechanochemical pattern formation in biological tissues". Biology Direct. 11: 22. doi:10.1186/s13062-016-0124-7. PMC 4857296. PMID 27145826.
  12. ↑ Tallinen et al. Nature Physics 12, 588–593 (2016) doi:10.1038/nphys3632
  13. ↑ Ball, 2009. Branches, pp. 52–59.
  14. ↑ Ball, 2009. Shapes, pp. 149–151.
  15. ↑ Duran-Nebreda, Salva; Pla, Jordi; Vidiella, Blai; Piñero, Jordi; Conde-Pueyo, Nuria; Solé, Ricard (2021-01-15). "Synthetic Lateral Inhibition in Periodic Pattern Forming Microbial Colonies". ACS Synthetic Biology. 10 (2): 277–285. doi:10.1021/acssynbio.0c00318. ISSN 2161-5063.
  16. ↑ 16.0 16.1 Tongway, D.J., Valentin, C. & Seghieri, J. (2001). Banded vegetation patterning in arid and semiarid environments. New York: Springer-Verlag. ISBN 978-1461265597. 
  17. ↑ 17.0 17.1 D'Avanzo, C. (22 February 2004). "Fir Waves: Regeneration in New England Conifer Forests". TIEE. Retrieved 26 May 2012.
  18. ↑ Meron, E (2019). "Vegetation pattern formation: the mechanisms behind the forms". Physics Today. 72 (11): 30–36. doi:10.1063/PT.3.4340.
  19. ↑ Meron, E (2018). "From Patterns to Function in Living Systems: Dryland Ecosystems as a Case Study". Annual Review of Condensed Matter Physics. 9: 79–103. doi:10.1146/annurev-conmatphys-033117-053959.
  20. ↑ 20.0 20.1 20.2 Gupta, Ankur; Chakraborty, Saikat (January 2009). "Linear stability analysis of high- and low-dimensional models for describing mixing-limited pattern formation in homogeneous autocatalytic reactors". Chemical Engineering Journal. 145 (3): 399–411. doi:10.1016/j.cej.2008.08.025. ISSN 1385-8947.
  21. ↑ Prigogine, I.; Nicolis, G. (1985), Hazewinkel, M.; Jurkovich, R.; Paelinck, J. H. P. (eds.), "Self-Organisation in Nonequilibrium Systems: Towards A Dynamics of Complexity", Bifurcation Analysis: Principles, Applications and Synthesis, Springer Netherlands, pp. 3–12, doi:10.1007/978-94-009-6239-2_1, ISBN 9789400962392
  22. ↑ 22.0 22.1 Gupta, Ankur; Chakraborty, Saikat (2008-01-19). "Dynamic Simulation of Mixing-Limited Pattern Formation in Homogeneous Autocatalytic Reactions". Chemical Product and Process Modeling. 3 (2). doi:10.2202/1934-2659.1135. ISSN 1934-2659.
  23. ↑ Marwaha, Bharat; Sundarram, Sandhya; Luss, Dan (September 2004). "Dynamics of Transversal Hot Zones in Shallow Packed-Bed Reactors†". The Journal of Physical Chemistry B. 108 (38): 14470–14476. doi:10.1021/jp049803p. ISSN 1520-6106.
  24. ↑ Greg Turk, Reaction–Diffusion
  25. ↑ Andrew Witkin; Michael Kassy (1991). "Reaction–Diffusion Textures" (PDF). Proceedings of the 18th Annual Conference on Computer Graphics and Interactive Techniques: 299–308. doi:10.1145/122718.122750. ISBN 0897914368. S2CID 207162368.


参考书目

  • Ball, Philip (2009). Nature's Patterns: a tapestry in three parts. 1:Shapes. 2:Flow. 3:Branches. Oxford. ISBN 978-0199604869. 


外部链接

  • SpiralZoom.com, an educational website about the science of pattern formation, spirals in nature, and spirals in the mythic imagination.
  • '15-line Matlab code', A simple 15-line Matlab program to simulate 2D pattern formation for reaction-diffusion model.


编者推荐

集智视频

集智学园

从涌现到斑图

集智斑图中级课程，由张江教授讲解涌现的本质。


涌现的本质究竟是什么？我们为什么会对涌现现象感到神秘莫测？答案就在于，大量个体会在斑图的世界中搭建一套全新的虚拟宇宙，而涌现恰恰发生于观察者对虚拟个体的界定与识别。


Pattern Formation

David Feldman

课程难度为中级，由David Feldman讲授。本节课程将主要围绕反应-扩散系统 reaction-diffusion systems，一种斑图生成 pattern formation动力学系统，说明了简单的动力学系统可以生成奇怪吸引子，无序或看起来无序的行为，蝴蝶效应，以及惊人复杂的模式。


我们已经展现了动力学系统可以具有混沌现象——不可预测的非周期性行为——但实际上动力学系统不止如此。本节课程将主要围绕反应-扩散系统，一种斑图形成动力学系统，说明了简单的动力学系统可以生成奇怪吸引子，无序或看起来无序的行为，蝴蝶效应，以及惊人复杂的斑图。


扩散，即物质弥漫最终产生随机运动的倾向，化学物质会从高密度区域运动向低密度地区，逐渐磨平浓度差异。扩散方程为:，D为扩散常数，即物质扩散得多快，是拉普拉斯算子:，u=u(x, y)是化学物质在(x, y)点的浓度。


反应-扩散系统是一种确定性的、空间扩展的动力学系统，描述了了两种化学物质的反应和扩散，它们的浓度分别为 u(x,y) 和 v(x,y)，相交于 f(u, v) 和 g(u, v)。该系统具有局部规则：，“下一个”u和v仅取决于其当前值和该点的导数。通常，u是活跃因素（activator），催化自身的增长；v是抑制因素，随着u的抑制而增长；v比u扩散得块，因此存在稳定的空间结构，不过依赖于扩散率 diffusion rates和系统几何学 system geometry。


反应扩散的结果可见于Experimentarium Digitale site以及Belousov Zhabotinsky实验 。比混沌系统更进一步，具有局部规则的简单的空间扩展性动力学系统就可生成稳定的全局斑图和结构。本节研究的反应-扩散系统仅仅是斑图形成系统的众多例子之一。


CSDN社区

斑图的matlab程序




本中文词条由11编译，CecileLi、 栗子CUGB审校，糖糖编辑，如有问题，欢迎在讨论页面留言。


本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。

取自“https://wiki.swarma.org/index.php?title=斑图生成&oldid=32351”