耗散律
所谓流网络中的耗散律是指每个节点的总流量[math]\displaystyle{ T_i }[/math]与该节点的耗散流[math]\displaystyle{ D_i }[/math]之间存在着幂律关系:
[math]\displaystyle{ D_i\propto T_i^{\gamma} }[/math]
其中[math]\displaystyle{ \gamma }[/math]是耗散律指数。耗散律指数在流网络中起着重要的作用,因为它关系到网络的集中化程度、鲁棒性以及生长。
各种流网络的耗散律
耗散律是各种流网络普遍具有的实证规律,下面我们针对不同的流网络分别来考察该实证规律。
生态流网络
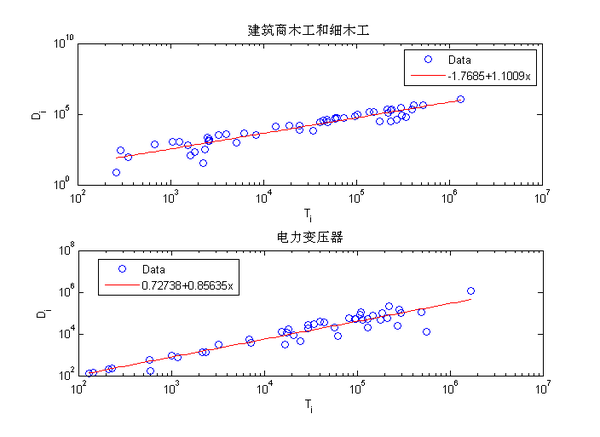
生态流网络描述的是多个物种之间的能量输运的网络,其中每个节点的耗散是指该物种由于呼吸、死亡等因素损失到环境中的能量。
图示为Mangwet和Baywet网络的耗散律[1]。
下表列出了19个生态流网络的耗散律指数与拟合优度[1][2]
| Network | γ | R2 |
|---|---|---|
| Baywet | 0.917 | 0.953 |
| Mangdry | 0.978 | 0.983 |
| Gramdry | 0.973 | 0.997 |
| Gramwet | 0.977 | 0.998 |
| CypDry | 0.957 | 0.949 |
| CypWet | 0.965 | 0.988 |
| Mondego | 0.979 | 0.997 |
| StMarks | 0.985 | 0.950 |
| Michigan | 0.995 | 0.999 |
| Narragan | 0.813 | 0.942 |
| ChesUp | 0.952 | 0.991 |
| ChesMiddle | 0.851 | 0.761 |
| Chesapeake | 0.985 | 0.985 |
| ChesLower | 0.926 | 0.971 |
| CrystalC | 0.959 | 0.995 |
| CrystalD | 0.963 | 0.996 |
| Maspalomas | 1.150 | 0.737 |
| Rhode | 1.200 | 0.963 |
国际贸易网
国际贸易网可以按照不同种产品细分为单种产品的贸易网,上图所示为2000年国际贸易网数据中,两类产品的贸易网络所形成的耗散律。它们的耗散律幂指数分别为1.1和0.86。
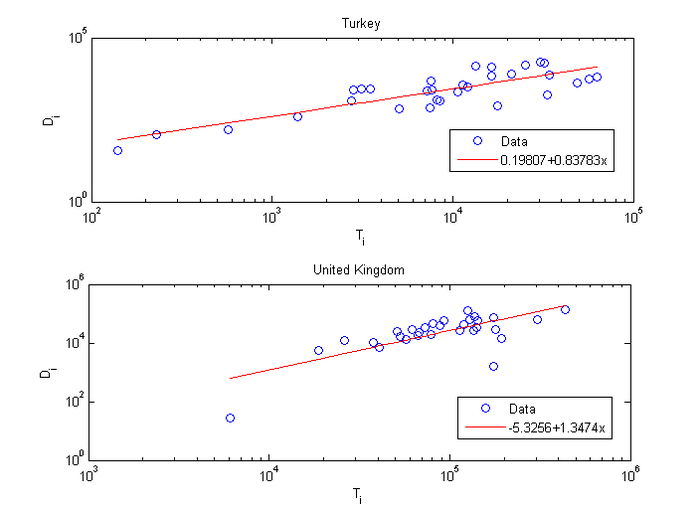
投入产出网
下图展示的是不同国家的投入产出表货币流的耗散律:
英国的耗散律指数大于1,土耳其的小于1。
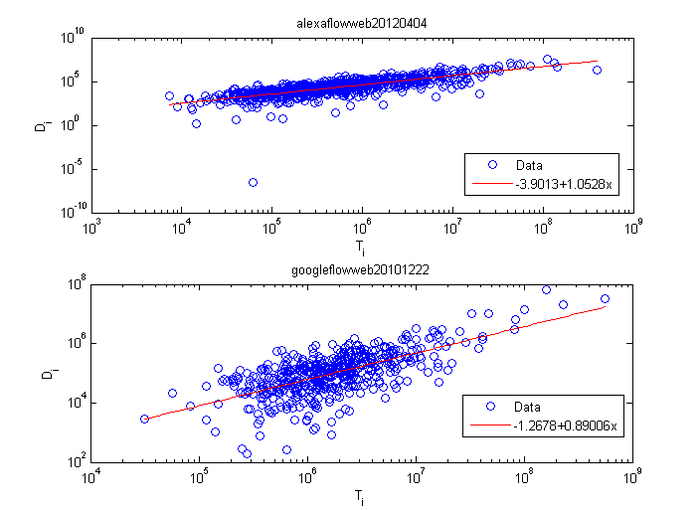
点击流网络
下图展示的是两个点击流网络的耗散律
耗散律指数及其意义
我们看到,不同流网络都遵循耗散律,但是有些网络的耗散律指数较大,有些则较小。如果我们将网络中的节点按照流量大小排序,则耗散律指数越大,那么大节点的耗散流比例也就会越大,这是因为若耗散律[math]\displaystyle{ D_i\propto T_i^{\gamma} }[/math]成立,则:
[math]\displaystyle{ \frac{D_i}{T_i}\propto T_i^{\gamma-1} }[/math]
上式左边表示耗散流占i节点总流量的比例,右侧为Ti的γ-1次幂,若γ>1,则随着流量Ti的增大则节点耗散的比例会增大,因此大节点会浪费更多的流。而当γ<1的时候,则耗散的比例会随着Ti的增大而减小,因此小节点的耗散比例要大于大节点。
耗散律指数能够影响整个流网络的异速标度律指数,因此耗散律指数越小,流网络越趋近于去中心化。而且耗散律指数能够影响流网络的鲁棒性。耗散律指数越大,则整个网络就越鲁棒,这是因为大量小节点分散了网络的流量。最后,耗散律指数可以影响网络的异速生长幂指数。
参考文献
- ↑ 1.0 1.1 Zhang, Jiang (2012). "Common Patterns of Energy Flow and Biomass Distribution on Weighted Food Webs".
{{cite journal}}: Cite journal requires|journal=(help); More than one of|first1=and|first=specified (help); More than one of|last1=and|last=specified (help); line feed character in|title=at position 43 (help) - ↑ Zhang, Jiang; Wu, Lingfei (2013). "Allometry and Dissipation of Ecological Flow Networks". Plos One.