伊辛模型 Ising Model

ISING模型简介

可以毫不夸张地说，Ising模型是统计物理中迄今为止唯一的一个同时具备:表述简单、内涵丰富、应用广泛这三种优点的模型。Ising模型的提出是为了解释铁磁物质的相变，即磁铁在加热到一定临界温度以上会出现磁性消失的现象，而降温到临界温度以下又会表现出磁性。这种有磁性、无磁性两相之间的转变，是一种连续相变（也叫二级相变）。Ising模型假设铁磁物质是由一堆规则排列的小磁针构成，每个磁针只有上下两个方向（自旋）。相邻的小磁针之间通过能量约束发生相互作用，同时又会由于环境热噪声的干扰而发生磁性的随机转变（上变为下或反之）。涨落的大小由关键的温度参数决定，温度越高，随机涨落干扰越强，小磁针越容易发生无序而剧烈地状态转变，从而让上下两个方向的磁性相互抵消，整个系统消失磁性，如果温度很低，则小磁针相对宁静，系统处于能量约束高的状态,大量的小磁针方向一致,铁磁系统展现出磁性。而当系统处于临界温度[math]\displaystyle{ T_C }[/math]的时候，Ising模型表现出一系列幂律行为和自相似现象。

由于Ising模型的高度抽象，人们可以很容易地将它应用到其他领域之中。例如，人们将每个小磁针比喻为某个村落中的村民，而将小磁针上、下的两种状态比喻成个体所具备的两种政治观点（例如对A,B两个不同候选人的选举），相邻小磁针之间的相互作用比喻成村民之间观点的影响。环境的温度比喻成每个村民对自己意见不坚持的程度。这样，整个Ising模型就可以建模该村落中不同政治见解的动态演化（即观点动力学 opinion dynamics）。在社会科学中，人们已经将Ising模型应用于股票市场、种族隔离、政治选择等不同的问题。另一方面，如果将小磁针比喻成神经元细胞，向上向下的状态比喻成神经元的激活与抑制，小磁针的相互作用比喻成神经元之间的信号传导，那么，Ising模型的变种还可以用来建模神经网络系统，从而搭建可适应环境、不断学习的机器（Hopfield网络或Boltzmann机）。

Ising模型之所以具有如此广泛的应用并不仅仅在于它的模型机制的简单性，更重要的是它可以模拟出广泛存在于自然、社会、人工系统中的临界现象。所谓的临界现象，是指系统在相变临界点附近的时候表现出的一系列的标度现象 Scaling phenomena，以及系统在不同尺度之间的相似性。临界系统之中不同组成部分之间还会发生长程的关联，这种通过局部相互作用而导致长程联系的现象恰恰是真实复杂系统，如社会、经济、认知神经系统的复杂性所在。因此，Ising模型不仅仅是一个统计物理模型，它更是一个建模各种复杂系统模型的典范。

ISING模型简史

Ising模型最早的提出者是Wilhelm Lenz (1920)。后来，他让他的学生Ernst Ising对一维的Ising模型进行求解，但是并没有发现相变现象，因此也没有得到更多物理学家的关注。随后，著名的统计物理学家Lars Onsager于1944年对二维的ISING模型进行了解析求解，并同时发现了二维ISING模型中的相变现象，从而引起了更多学者的注意。之后，随着物理学家Landau、Ginzburg等人的努力，人们发现了Ising模型与量子场论之间的联系，并创立了平行的“统计场论”

模型表述

考虑一个如下图所示的晶格世界:

网格上的小磁针

假设第[math]\displaystyle{ i }[/math]个节点是一个小磁针（或者一个村民），每个小磁针有上下两种状态（村民有上,下两种意见），我们用[math]\displaystyle{ s_i }[/math]来表示这个状态，并且

[math]\displaystyle{ s_i=\left\{\begin{array}{ll} +1 & \\ -1 & \end{array}\right. }[/math]

表示磁针朝上或者朝下。网格上相邻的两个小磁针可以发生相互作用。

总能量

我们可以通过总能量的概念来刻画这种相互作用：即如果两个相邻方格的小磁针状态一致（例如都是朝上），则系统的总能量减1单位，否则如果不同就加1单位。外界还可能存在磁场，如果小磁针方向与外场方向一致，则能量也会降低。我们定义总能量：

[math]\displaystyle{ E_{\{s_i\}}=-J\sum_{\lt i,j\gt }{s_is_j}-H\sum_{i}^N{s_i} }[/math]

其中[math]\displaystyle{ J }[/math]为一个能量耦合常数，[math]\displaystyle{ E_{\{s_i\}} }[/math]表示系统处于状态组合[math]\displaystyle{ \{s_i\} }[/math]下的总能量。求和下标[math]\displaystyle{ \lt i,j\gt }[/math]表示对所有相邻的两个小磁针进行求和。我们看到，如果[math]\displaystyle{ s_i=s_j }[/math]，则总能量就会减少J。H表示外界磁场的强度,它是一个参数，如果外界磁场向上H为正，否则为负。如果某个小磁针的方向与外场一致，则总能量减少一个单位。

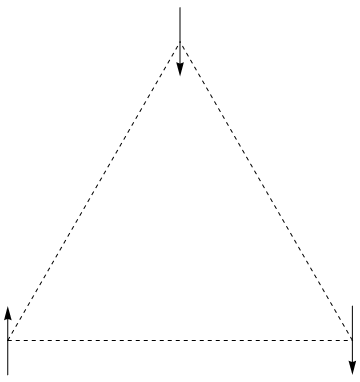
例如，假设系统中仅仅有3个小磁针，它们彼此相连（虚线表示构成邻居关系）形成一个三角形，如图：

每个小磁针有+1,-1两种可能状态，那么所有的状态组合就包括：

[math]\displaystyle{ \{s_i\}=\{+1+1+1,+1+1-1,+1-1+1,+1-1-1,-1-1+1,-1+1+1,-1+1-1,-1-1-1\} }[/math]

那么这8种状态组合，每一个都对应一个唯一的能量值，它们分别是：

[math]\displaystyle{ E_{\{+1+1+1\}}=-J(1\times 1 + 1\times 1+ 1\times 1)-H(1+1+1)=-3J-3H, }[/math]

[math]\displaystyle{ E_{\{+1+1-1\}}=-J((1\times 1)+(1\times (-1))+((-1)\times 1))-H(1+1-1)=J-H, }[/math]

[math]\displaystyle{ E_{\{+1-1+1\}}=J-H, E_{\{+1-1-1\}}=J+H,E_{\{-1+1+1\}}=J-H, }[/math]

[math]\displaystyle{ E_{\{-1+1-1\}}=J+H, E_{\{-1-1+1\}}=J+H, E_{\{-1-1-1\}}=-3J+3H }[/math]

系统中小磁针的相互之间以及与外场方向一致的话，则系统的能量就低。所以+1+1+1为能量最小的状态。沿用村民的比喻来说，系统的能量相当于村民观点存在的冲突的数量。如果两个相邻的村民意见不一致，总冲突数就+1，否则就减1。而外场建模了观点的媒体宣传效应,如果村民的观点与舆论宣传一致，则能量越低，因此也越和谐。

温度

但是，系统的演化并不完全由总能量决定。由于小磁针处于噪声环境中，热涨落又会引起小磁针的状态随机反转。我们可以用温度[math]\displaystyle{ T }[/math]来衡量这种环境影响的随机性。T越高，则小磁针发生反转的概率就会越大。

这样，有两种力作用在小磁针上，一种力来源于小磁针邻居以及外场对它的影响，这种影响倾向于使得相邻的邻居彼此状态一致以及与外场尽量一致，即尽量使得系统的总能量达到最小。另外一种力则来源于环境噪声的扰动，它迫使小磁针无视邻居的作用而发生随机的状态反转。于是，每个小磁针就挣扎于这两种不同的力量之间。不难想象，假如温度[math]\displaystyle{ T }[/math]趋于0，则每个小磁针都会与外场相一致，那么，最终系统将处于全是+1或者全是-1的状态（取决于外场H是正还是负）。假如T特别高，而相互作用强度J特别小，则邻居间的作用可以忽略，每个小磁针都完全随机地取值。

这样，整个Ising模型就有两个外生给定的参数[math]\displaystyle{ T,H }[/math]来表示环境的温度和磁场强度。在村民的比喻中,温度相当于村民进行观点选择的自由程度，温度越高，村民选择观点越随机，而不受自己周围邻居的影响；否则村民的选择严重依赖于邻居和媒体宣传。

蒙特卡罗模拟

具体算法

下面我们来讨论Ising模型的计算机模拟。有趣的是，Ising模型的模拟方法与我们熟悉的模拟方法很不同，它并没有为每个小磁针制定状态转变的规则，而是先让每个小磁针的状态发生随机变化，再根据能量来依概率接受这种状态变化。

具体作法是：在每一个仿真周期，模拟程序会根据当前的状态组合[math]\displaystyle{ s_{i}(t) }[/math]，进行小的改进（例如随机翻转某一个小磁针），得到一个新的状态组合[math]\displaystyle{ s_i' }[/math]。 但是系统下一时刻的状态并不是直接取为该状态组合，而是以概率发生：

[math]\displaystyle{ s_i(t+1)=\left\{\begin{array}{ll} s_i' & \mbox {with probability } \mu, \\ s_i(t) & \mbox {with probability }1-\mu.\end{array}\right. }[/math]

其中,概率[math]\displaystyle{ \mu }[/math]按照如下公式计算：

[math]\displaystyle{ \mu=\min{\{\exp{((E(s_i(t))-E(s_i'))/(kT))},1\}} }[/math]

也就是说，系统会按照概率[math]\displaystyle{ \mu }[/math]接受新的状态组合[math]\displaystyle{ s_i' }[/math]。其中[math]\displaystyle{ \mu }[/math]与新状态组合能量与当前能量的差值以及温度有关。如果状态组合[math]\displaystyle{ s_i' }[/math]的能量值大于原状态组合[math]\displaystyle{ s_i(t) }[/math]的能量值，则[math]\displaystyle{ \mu\lt 1 }[/math]但不为0，所以系统有可能接受这个状态组合。如果[math]\displaystyle{ E(s_i')\lt E(s_i(t)) }[/math]，则[math]\displaystyle{ \mu=1 }[/math]，则系统肯定会接受状态组合[math]\displaystyle{ s_i' }[/math]。这样，系统会更加倾向于往能量减少的状态组合方向演化，但是也会以一定的概率演化到能量大的状态组合，这种演化到能量较大的状态组合的概率由参数T确定。如果T越大，则系统接受一个能量较高状态组合的概率也会越大，也就是说系统越随机。否则系统会比较规矩地沿着能量下降的方式演化，系统相对秩序。

按照这个接受概率规则，每一时刻，系统生成一个新的候选状态组合，然后再根据能量的大小决定是否接受它。于是，就进行了一步系统演化。按照上述算法，系统可以最终达到如下的概率分布状态：

[math]\displaystyle{ p(\{s_i\})=\frac{1}{Z}\exp(-\frac{E_{\{s_i\}}}{kT}) }[/math]

这个分布就是著名的玻尔兹曼分布，其中[math]\displaystyle{ k }[/math]为玻尔兹曼常数，等于[math]\displaystyle{ 1.3806488\times 10^{23} }[/math]，[math]\displaystyle{ Z }[/math]为归一化因子：

[math]\displaystyle{ Z=\sum_{\{s_i\}}\exp(-\frac{E_{\{s_i\}}}{kT}) }[/math]

其中，求和符号是针对所有可能的状态组合的。这样可以保证概率归一：

[math]\displaystyle{ \sum_{\{s_i\}}p(\{s_i\})=1 }[/math]

在统计物理中，[math]\displaystyle{ Z }[/math]又称为系统的配分函数，它是温度[math]\displaystyle{ T }[/math]和外场[math]\displaystyle{ H }[/math]的函数，即：[math]\displaystyle{ Z(T,H) }[/math]。这个函数非常重要，因为它决定了系统的各种热力学性质。

在玻尔兹曼分布中，每个状态组合出现的概率将会与该状态组合下的总能量的负值呈现指数关系。也就是说，能量越小，该状态组合的出现概率也就越大。反之，出现概率会随着能量增加而快速衰减。并且温度T会对衰减速度起到调节作用。这里出现概率的具体含义是指：如果针对同样参数和初始条件的Ising模型进行多次重复试验。运行很长时间后，我们观察这些Ising模型处于什么样的状态组合，则某一状态组合在若干实验中的出现频率会接近波尔兹曼分布。用统计物理的术语来说，这些试验就称为一个系综。

因为已知在现实的铁磁物质中，系统与环境的热交换构成了一个统计物理中的正则系统，系统最终会达到玻尔兹曼分布的状态，所以为了模拟真实的铁磁物质，Ising模型也应该达到这个稳态分布。我们可以从数学上证明，上述随机过程的稳态分布就是根据统计力学计算出来的分布结果。这种模拟方法就是Ising模型的马尔科夫链-蒙特卡罗模拟方法 Markov Chain Monte Carlo(MCMC），也叫做Metropolis-Hastings算法。

细致平衡条件

和另一种常用的MCMC技巧吉布斯采样 Gibbs Sampling类似，它的状态转移矩阵也满足细致平衡条件 Detailed Balance Equations：

若[math]\displaystyle{ p_x }[/math]与[math]\displaystyle{ p_y }[/math]分别为状态[math]\displaystyle{ x }[/math]，[math]\displaystyle{ y }[/math]在平稳分布中的概率，[math]\displaystyle{ p(x,y) }[/math]与[math]\displaystyle{ p(y,x) }[/math]分别为前述设定的状态转移概率（转移概率矩阵中的元素），则有

[math]\displaystyle{ p_x p(x,y)=p_y p(y,x) }[/math]

值得注意的是，如果我们只定义马尔科夫链的转移概率矩阵满足对于任意的状态链[math]\displaystyle{ \{x_0,x_1,....x_n\} }[/math]，存在

[math]\displaystyle{ \frac{p(x_0,x_1)p(x_1,x_2)...p(x_{n-1},x_n)}{p(x_1,x_0)p(x_2,x_1)...p(x_n,x_{n-1})} = \frac{p(x_0,x_n)}{p(x_n,x_0)} }[/math]

则该马尔科夫链形成的唯一平稳分布自然满足细致平衡条件的要求。

模拟结果

状态组合

首先，我们可以将+1对应为黑色，-1对应为白色，从而用图表示出在不同温度下系统达到稳态的模拟结果，如下图：

在图中，不同的行对应了不同的温度值。第一行的温度[math]\displaystyle{ T\gt T_C }[/math]，第二行[math]\displaystyle{ T\approx T_C }[/math]，第三行[math]\displaystyle{ T\lt T_C }[/math]。其中，[math]\displaystyle{ T_C }[/math]为临界温度，我们将在后面介绍如何计算该数值。当温度小于临界值的时候，Ising模型中大多数磁针都取相同的颜色，系统处于较为秩序的状态。当温度大于临界值的时候，每个小磁针的颜色会比较混乱无序，系统处于随机的状态。而当温度接近临界的时候，系统的运行介于随机与秩序之间，也就是进入了混沌边缘地带。我们将这种状态称为临界状态。

需要明确的是，上述截图仅仅是在成千上万种可能状态组合中的一种，但是却是最可能的一种（即概率较大的一种）。因为根据玻尔兹曼分布表达式，原则上讲，无论T和H为多少，任何一种状态组合[math]\displaystyle{ \{s_i\} }[/math]都有可能，但是可能性会随着状态组合的能量增加而迅速衰减。因此我们会以较大的概率看到那些能量小的状态。

热力学量

除了从图形定性地看出Ising模型的运行以外，我们还可以研究模型的热力学性质，从而考察这些宏观量在稳态条件下如何依赖于参数，并与实验结果进行比较。以下结果都是对2维Ising模型的模拟或计算结果。

平均磁矩

首先，可以定义平均磁矩这个量。如果将所有小磁针+1或-1的状态进行代数和，可以得到：

[math]\displaystyle{ M_{\{s_i\}}=\sum_{i=1}^N{s_i} }[/math]

其中[math]\displaystyle{ N }[/math]为系统中所有小磁针的个数。[math]\displaystyle{ M_{\{s_i\}} }[/math]就是系统中在给定状态[math]\displaystyle{ s_i }[/math]条件下，总的磁矩（每个小磁针向上或者向下都是矢量）。在稳态条件下，系统满足平衡分布，那么，对所有可能的状态按照它们出现的概率进行加权平均就得到了整个系综的平均磁矩（即对所有可能的实验结果求平均）：

[math]\displaystyle{ \langle M\rangle =\sum_{\{s_i\}}{M_{\{s_i\}}p_{\{s_i\}}}=\frac{1}{Z} \sum_{\{s_i\}}{M_{\{s_i\}}\exp (-E_{\{s_i\}}/(kT))} }[/math]

对应的每个小磁针的平均磁矩为：

[math]\displaystyle{ m=\frac{\langle M\rangle}{N} }[/math]

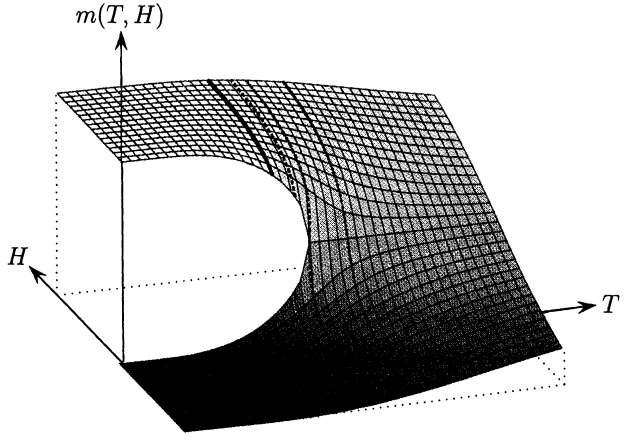
通过计算机模拟实验，也可以通过平均场近似方法解析地给出平均磁矩随参数[math]\displaystyle{ H }[/math]和[math]\displaystyle{ T }[/math]的变化情况：

注意，这张图在[math]\displaystyle{ H=0 }[/math]的位置发生了断裂，这意味着系统在此参数附近存在着突变的现象。另外，当我们从[math]\displaystyle{ H=0 }[/math]这个截面观察该图形，会发现，当[math]\displaystyle{ T }[/math]比较小的时候，[math]\displaystyle{ m }[/math]的值同时存在两个分支，一个大于0，一个小于0。这表明，当外界磁场消失以后，如果温度足够低低于临界数值[math]\displaystyle{ T_C }[/math]的话，小磁针的平均方向可能朝上也可能朝下，系统出现了对称性破缺。图中豁口的交汇点对应的恰恰是临界温度[math]\displaystyle{ T_C }[/math]的位置。如果[math]\displaystyle{ T\gt T_C }[/math]，则[math]\displaystyle{ m }[/math]始终为0，系统处于对称的状态。进一步，我们还可以画出[math]\displaystyle{ m }[/math]在不同参数T下随参数H的变化图：

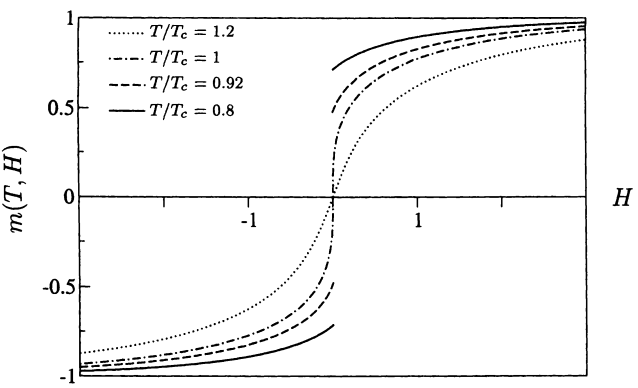
这张图更加清晰地揭示出系统发生了相变。首先，我们看到当[math]\displaystyle{ T\lt T_c }[/math]的时候，m随H的曲线发生了断裂。也就是说当H值连续地从小于0变到大于0的时候，热力学量[math]\displaystyle{ m }[/math]从小于0不连续地变到了大于0。这种热力学函数随参数发生不连续的变化现象称为一级相变。当[math]\displaystyle{ T=T_C }[/math]的时候，这条[math]\displaystyle{ m }[/math]对[math]\displaystyle{ H/\lt math\gt 的曲线又连接到了一起，没有在\lt math\gt H=0 }[/math]的点发生断裂。但如果我们考察m-H曲线的斜率会发现，斜率是无穷大。当热力学量随某一参数的变化连续，但是导数发散的时候，我们称该系统正在发生二级相变，也叫连续相变。

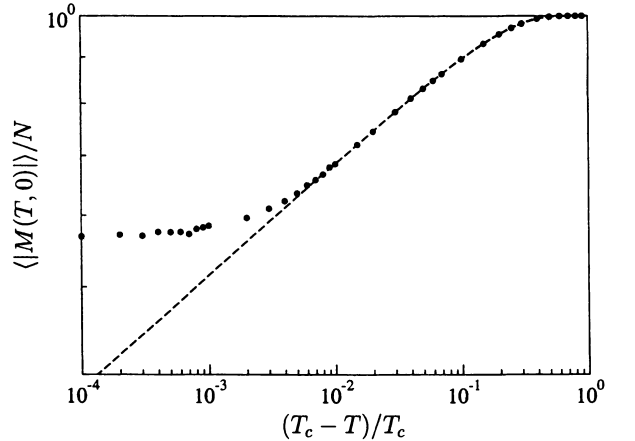
为了更深入地理解[math]\displaystyle{ m }[/math]值在临界点[math]\displaystyle{ T=T_C, H=0 }[/math]附近的行为，我们将研究[math]\displaystyle{ m }[/math]与归一化的温度([math]\displaystyle{ (T_C-T)/T_C }[/math])的关系如下图：

上图表示了[math]\displaystyle{ m }[/math]随归一化温度呈现出幂律规律的变化，可以用如下公式表示：

[math]\displaystyle{ m_0\sim (\frac{T_C-T}{T_C})^{\frac{1}{\beta}} }[/math]

其中该关系的幂指数[math]\displaystyle{ \beta }[/math]模拟数值接近于8。

磁导率

除了磁矩的平均值，我们还可以计算出磁矩的涨落，我们将这个平均涨落称为磁导率，定义如下：

[math]\displaystyle{ \chi{(T,H)}=\frac{\langle M^2\rangle -\langle M\rangle^2}{NkT} }[/math]

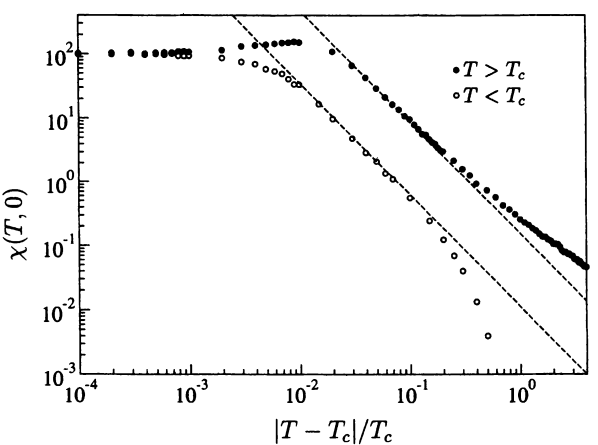
类似地，我们将磁导率与归一化温度曲线画在双对数坐标下得到一条直线(当[math]\displaystyle{ H=0 }[/math])：

图中的黑色曲线表示[math]\displaystyle{ T\gt T_C }[/math]的结果，开放圆圈表示[math]\displaystyle{ T\lt T_C }[/math]的结果。这个幂律行为可以用公式：

[math]\displaystyle{ \chi\sim (|T-T_C|/T_C)^{-\gamma} }[/math]

表示,其中指数[math]\displaystyle{ \gamma }[/math]约等于7/4。

比热

按照类似的方法，我们还可以定义系综的平均能量：

[math]\displaystyle{ \langle E\rangle =\frac{1}{Z} \sum_{\{s_i\}}{E_{\{s_i\}}\exp (-E_{\{s_i\}}/(kT))} }[/math]

能量的平均涨落就是比热：

[math]\displaystyle{ c=\frac{\langle E^2\rangle-\langle E\rangle^2}{NkT^2} }[/math]

在0外场情况下，比热在临界点附近也呈现出与归一化温度的幂律关系：

[math]\displaystyle{ c\sim (|T-T_C|/T_C)^{-\alpha} }[/math]

关联强度

每个小磁针都是一个随机变量，我们可以计算任意两个小磁针i,j的统计关联性，从而考察相隔任意距离的两个小磁针是否具有联系。 具体地，我们定义关联强度为：

[math]\displaystyle{ g(i,j)=\langle (s_i-\langle s_i\rangle)(s_j-\langle s_j\rangle)\rangle=\langle s_is_j\rangle-\langle s_i\rangle \langle s_j\rangle }[/math]

通过模拟我们发现，相关函数仅仅与两个小磁针之间的距离[math]\displaystyle{ r }[/math]有关，并且当温度远离临界温度的时候，相关函数与距离的函数呈现指数衰减：

[math]\displaystyle{ g(r_{ij})\sim \exp(-r/r_0) }[/math]

其中，[math]\displaystyle{ r_0 }[/math]为一常数，称为特征尺度。也就是说，任意两个磁针的统计相关性会随着它们彼此之间的距离增长而快速衰减，只要距离稍大于特征关联尺度，则关联性就会接近于0。但是，在临界温度附近，两磁针之间的统计相关性却呈现出幂律的形式，即：

[math]\displaystyle{ g(r_{ij})\sim r^{-(d-2+\eta)} }[/math]

其中[math]\displaystyle{ d }[/math]为Ising模型所在空间的维度，[math]\displaystyle{ \eta }[/math]为幂律指数。幂律衰减会比指数衰减慢很多，这也就意味着两磁针之间的关联长度会很长。假如我们仍然用指数函数来拟合相关性的衰减，即假设[math]\displaystyle{ g(r_{ij})\sim \exp(-r/r_0) }[/math]在临界温度的时候仍然成立,那么[math]\displaystyle{ r_0 }[/math]就可以写为：

[math]\displaystyle{ r_0\sim |\frac{T_C-T}{T_C}|^{-\nu} }[/math]

所以，当[math]\displaystyle{ T\rightarrow T_C }[/math]的时候，特征尺度[math]\displaystyle{ r_0\rightarrow \infty }[/math]。也就是说，小磁针彼此发生了长程相关：局部的空间涨落会通过某种合作机制传递并影响了相隔很远的小磁针。

临界相变

通过上述的讨论，我们已经对Ising模型的提出、模拟办法以及得到的一系列模拟、计算结果进行了粗略的介绍。我们看到，Ising模型的美妙之处就在于从一个相对简单而干净的模型出发，仅通过两个自由参数[math]\displaystyle{ H }[/math]和[math]\displaystyle{ T }[/math]，就可以复制出真实铁磁物质的相变行为。尤其是当系统处于临界参数的时候，即温度[math]\displaystyle{ T=T_C }[/math]，外界磁场强度H为0，系统展现出来的是二级相变（连续相变）。系统一切宏观热力学量都展现出标度行为，我们将这种特殊的相变称为临界相变，而将系统所体现出来的标度（幂律）行为、长程相关等现象统称为临界现象。

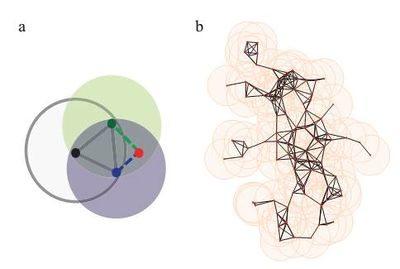
临界现象不仅仅是ISING模型、铁磁物质所独有的，它具有相当的普遍性。它会在很多复杂系统中体现出来，例如气-液相变过程、湍流，甚至股票市场、经济系统等。临界系统体现出的一个重要特征就是：自相似性和长关联性。Ising模型临界状态模拟图如下：

这是在外场[math]\displaystyle{ H=0 }[/math]，温度刚好等于临界温度的时候各个小磁针构成的一个构型。该图中，同一种颜色（即状态一致）的小磁针形成了彼此连通的团簇。这些团簇的尺寸有大有小。单独一个团簇具有一定的自相似性，它构成了一个分形。并且团簇的形态会在多个尺度重现类似的模式。假如我们将系统放大或者缩小，我们将无法分辨出不同之处，这就是无标度性这个名词的来源。

当系统处于临界状态的时候，它的行为会呈现出一定的普适性。即无论系统的微观作用规则如何，系统的临界参数、各种热力学量的临界指数（如[math]\displaystyle{ \alpha,\beta,\gamma }[/math]等）都相同。因此，人们将具有相同临界指数的模型类划分为普适类。拿Ising模型来说，无论Ising模型位于什么样的空间中（例如四方晶格、六角格、三角格等），它们的微观规则也可能略有不同，但是，所有这些Ising模型都属于同一个普适类，也就是说它们具有相同的临界温度和临界指数。

另外一个表现出临界行为以及临界相变的简单例子就是渗流模型。

ISING模型的重整化

目前，求解Ising模型的方法主要包括：模型的解析求解、平均场近似的方法、Landau的近似方法、以及重正化群的方法等。其中，重正化群方法与众不同，它是直接从模型达到临界后所展现出来的自相似性出发，写出重正化方程以及重正化算符。那么临界温度和各种临界指数就可以从该算符的线性化中求出。更有趣的是，由重正化群技术出发，我们自然可以得出所谓的“普适类”的概念：即存在一类Ising模型，虽然他们的微观规则很不相同，但是却具有相似的临界指数。实际上，这些模型都处于同一个普适类曲面上，即它们经过无穷多次重正化操作后都会收敛到相同的不动点。

更多应用

Ising模型目前应用非常广泛。本小节主要从社会科学和神经科学这两个方面介绍它的应用。

投票模型 Voter Model

在社会科学应用方面，我们主要介绍一个叫做投票的模型。假设有一个村落，每家每户都规则地排列在一个网格上。每个人都有自己的政治观点，假设第i个村民的政治观点是[math]\displaystyle{ s_i }[/math]，其中[math]\displaystyle{ s_i }[/math]可以在有限状态集合V中取值。我们用不同的颜色来表示不同人的政治观点，如下图所示：

这张图展示了模型的一个瞬间的状态，其中每个村民都有6种不同的政治观点，它们被表达为6种不同的颜色。

Voter模型的演化规则如下：每一个时刻，有n个村民会改变自己的政治观点，他们会随机地从自己周围的八个邻居中选择一个邻居，拷贝他的政治观点（被他的邻居说服了）。n越大，就会有越多的村民改变自己的观点，系统变化会很快，而n越小，则系统演化就会越慢。

随着模型的演化，相同观点的人们开始形成团簇，如图所示：

如果模型继续演化，则6种观点中的5个将会消失，只剩下一种观点，但具体是哪一个我们无法预测。但我们可以确定系统必然收敛到一种确定的政治观点，这是因为该模型等价于一个带吸收壁的随机游走，系统将最终收敛。

然而，如果我们稍作变化，只要每个村民在每个周期都会有一个小概率v发生政治观点的随机变化（并不拷贝邻居的颜色）。那么这个系统就将持续演化下去，不会停留在固定的状态上。不难看出，在这种改进的模型中，Voter模型与Ising模型很相似。其中，村民拷贝邻居的观点相当于Ising模型中，小磁针朝能量减小的方向演化。而每个村民按小概率v发生观点随机变化就相当于环境噪声的影响。如果适当地选择v参数的大小，Voter模型将会达到和ISING模型类似的效果，即存在着临界的概率[math]\displaystyle{ v_C }[/math]，使得系统处于临界状态。与ISING模型不同的是每个村民的状态取值可以更多。

对比Voter模型和Ising模型不难发现，Voter模型中并不存在能量，但是给出了每个微观个体状态转变的具体规则，而在Ising模型中，单个小磁针的状态改变没有具体的规则，但是系统整体定义了总能量，于是只有那些可以使得总能量变小的微观个体转变才更容易被接受。当运行起来以后，Voter模型与Ising具有相似的行为，这意味着这两种状态更新方式存在着一定的等价性。我们看到，Voter模型中每个村民拷贝某个邻居的观点相当于使得这两个格点的状态乘积尽量等于1（当有+1,-1两个状态的时候），也相当于降低系统整体的能量。反过来，要想降低Ising模型中的总能量，一种明智的方法就是使得两个相邻格点的小磁针状态一致。由此可见，这两种模型存在着天然的对应。也意味着，我们可以定义Voter模型的能量函数，也可以为Ising模型指定微观演化的规则。

与此类似的社会学模型还有很多，例如著名经济学诺贝尔奖得主Thomas C. Schelling的种族隔离模型也是一个类似的温度[math]\displaystyle{ T=0 }[/math]的Ising模型。种族隔离模型假设一个街区中随机分布着两种肤色的人，例如黑人和白人。假如一个黑人周围的白人过多，则黑人会搬家（移动到周边的方格），否则如果白人周围是黑人，他也会搬家。这样经过足够长时间的演化，系统将形成不同的肤色的区块。这个模型与Ising模型有很多相似的地方。

Hopfield神经网络模型

Ising模型的一个显著的性质就是，随着系统的演化，它的能量会自发地降低。我们前面已经提到这种让整体降低能量的方法实际上与拷贝邻居状态的微观原则一致。于是，我们可以设计一种微观的演化机制，而使得宏观的某种待优化的函数（例如能量）能够自然地被优化。这就是Hopfield网络模型的起源。

Hopfield网络是一个著名的神经网络模型，通过对网络进行训练，可以让它记住相应的模式，并在适当的条件下联想回忆提取出相关的模式。也就是说，Hopfield模型通过训练（改变相互连接的权重），可以将要记忆的模式映射为能量最小的状态，之后通过Ising模型的邻域相互作用规则自发演化到这种最小能量状态。Hopfield的构造如下，一个加权的网络，如下图，每个节点都是一个神经元，加权的连边表示神经元之间的突触连接。

假设每个神经元有两种状态：激活、未激活，分别用[math]\displaystyle{ s_i=+1,-1 }[/math]来表示。神经元i到j的连接权重用[math]\displaystyle{ w_{ij} }[/math]来表示。

在初始时刻，我们把输入向量映射为每个神经元的激活、未激活状态。然后，Hopfield网络的运行规则如下，在每一个仿真周期，每个神经元根据下述规则更新状态：

[math]\displaystyle{ s_i(t+1)=\left\{\begin{array}{ll} 1 & \mbox {if }\sum_{j}{w_{ij}s_j(t)}\gt \theta_i, \\ -1 & \mbox {otherwise.}\end{array}\right. }[/math]

这里[math]\displaystyle{ \theta_i }[/math]为阈值常数。根据这条规则，如果与神经元i相邻的所有神经元都激活，并且它们的连接权重为正的话，那么该神经元就有可能被激活。这就相当于最小化一个全局的能量函数，能量函数定义为：

[math]\displaystyle{ E_{\{s_i\}}=-\sum_{ij}w_{ij}s_is_j - \sum_{i} \theta_i s_i }[/math]

那么，Hopfield网络按照上述规则运行就会使得总能量尽量降低。相比较Ising模型，我们看到，Hopfield的能量函数与Ising模型非常相似，所不同的是相互作用强度因连接而异([math]\displaystyle{ w_{ij} }[/math])，同时外场:[math]\displaystyle{ \theta_i }[/math]也会因神经元不同而不同。因此，可以说Hopfield网络就是一个变种的Ising模型。

另外，要想让Hopfield网络完成联想记忆，还需要给该网络进行训练。所谓的网络训练，就是要通过一定的规则来改变神经元之间的连接权重[math]\displaystyle{ w_{ij} }[/math]。假设我们希望Hopfield网络能够记住一组特定的向量（例如[math]\displaystyle{ V_1,V_2,V_3,...,V_{m} }[/math])其中[math]\displaystyle{ m }[/math]为待学习的向量的个数，每一个向量可以写为：

[math]\displaystyle{ V_i=\lt 1,-1,1,\cdot\cdot\cdot,1\gt }[/math]

其中向量的长度为[math]\displaystyle{ n }[/math]。我们按照如下的规则来调解权重：

[math]\displaystyle{ w_{ij}=\sum_{\nu=1}^{m}V_{\nu}(i)V_{\nu}(j) }[/math]

[math]\displaystyle{ V_{\nu}(i) }[/math]表示要学习的第[math]\displaystyle{ \nu }[/math]个向量的第i个分量的值。

按照这种方式对整个网络进行训练之后，我们就得到了一组权重[math]\displaystyle{ w_{ij} }[/math]。之后，我们就用这组权重作为Hopfield网络中的连接权重，然后针对任意一个输入数据作为神经元的初始状态，按照Hopfield的运行规则演化，系统将逐渐收敛到已记忆过的向量[math]\displaystyle{ V_1,V_2,V_3,...,V_{m} }[/math]中的一个。

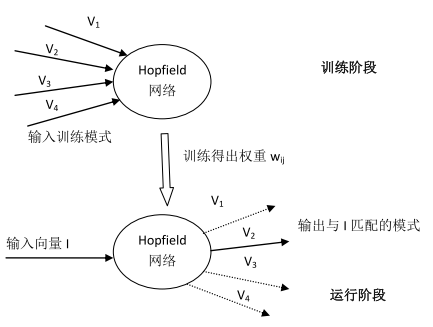
总结来看，Hopfield网络的运行分为两个阶段，它们的输入数粗示意图如下所示：

参考文献

Christen, Kim (2006). 复杂性和临界状态. 复旦大学出版社. ISBN 9787309052022. 

参见

• ISING模型的重正化
• 投票模型
• Hopfield网络

编者推荐

复杂网络上的Ising模型

集智文章

复杂网络上的Ising模型

本文将复杂网络与Ising模型结合，使用随机几何图模型，构造复杂网络，并在网络的基础上运行Ising模型。探索了其临界温度，发现临界温度与粒子数具有密切关联。同时发现相邻的集团之间，具有较强的独立性，并做了具体的数值分析。临界温度与独立性包涵了重要的现实意义，对于物质生长、凝聚具有解释效力；对于很多社会问题，也可以基于此模型给出解释 。

集智课程

相变与相变模型

本课程的主题是相变，它是一种涌现的模式，是系统表现出来的某种性质在不同情况下的变化。除了相变之外，在本课中还会向大家介绍大名鼎鼎的“Ising Model”，最后，还将简单介绍沙堆模型的相关内容。

平衡态伊辛模型的本征微观态及本征值

本课程中，展示了 Ising 模型的蒙特卡洛模拟验证了本征微观态相变理论与有限尺度标度理论，并在全球气温系统中进行了实证分析。

复杂系统中的关联

计算了理想玻色气体的关联函数与关联长度,得到高温时，关联长度较短，趋于临界点的时候，关联长度趋于无穷大的结论，并引入了复杂系统的单元-单元关联函数，通过Ising 模型计算模拟数据证实本征值满足有限尺度标度关系。

---

本中文词条由Jake参与编译，薄荷编辑，欢迎在讨论页面留言。

本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。