系统中的观察者(3)——物理中的观察者

物理中的观察者

测量

这一章，我们将走进形而下的世界，讨论物理学中的两大基石：量子力学和统计力学。与以往的物理教科书不同的是，我们将以一种观察者的视角重新看待这些学科，甚至将很多表面上丝毫不相干的学术理论重新联系到一起。需要事先指出的是，我们在这里讨论这两门学科并不想从观察者论的角度重新提出量子和统计的基础，更不想推翻它们，而是想尝试从观察者的角度去理解它们，以至于可以把这两门学科获得的很多知识最终为观察者理论所用。

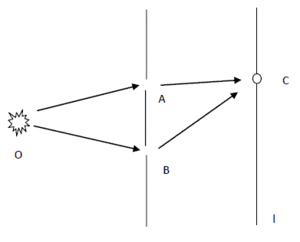
从物理的角度探讨观察者的问题始于我们对外在事物的测量，它可以用下面这张图来概括：

图3-1

按照传统的认识，一次测量就是一次从真实世界向观察者世界中的信息投射。之所以现实世界上面加了引号，以及其中的物体用虚线表示是因为按照量子力学的说法，这个世界并不像我们感受的那样真实。观察者的世界也就是观察者测量的结果才是真正真实、可靠的东西。假设一个所谓“真实的”客观世界并无太大意义，因此我们不如将上面的图转换成下面的图：

图3-2

我们不需要假设一个外界存在的世界，观察者面对的只是一次一次的测量，这些测量构造了一个观察者的世界。从这个角度来说，无论是量子力学还是统计力学都不过是在叙述观察者测量过程中的规律。

从量子力学到量子概率

量子物理起源于人们对微观物质运动规律的探讨，后来经过爱因斯坦、玻尔、薛定鄂、海森堡、狄拉克等人努力，量子力学作为一套能够成功描述微观粒子运动规律的数学产生了（参见《上帝掷骰子吗？》）。力学 mechanics与物理 physics的最大区别就在于力学给出的是一种抽象的数学结构或者框架，它虽然抽象自物理但却可以没有真实的物理对应。虽然物理学家发明了这套数学，但是很少有人真正相信它的真实含义和作用。人们更加倾向于认为量子力学不过是一套过渡规律，背后一定还存在着更底层的客观实在。
只有少数几个科学家在一开始就不去争论量子力学背后是否有更底层的客观实在，而是单从数学的角度为量子力学奠定基础，其中一个最有名的人就是伟大的数学家冯.诺依曼。他发现，其实量子力学的背后蕴藏着一种很深的数学体系，而这个数学体系对于传统的Kolmogrov的概率论进行了很大的修改，也就是说，其实量子力学真正的数学基础不是别的，正是一种全新的概率论，后人将这套概率论称之为“量子概率 quantum probability”。

目前市面上有很多关于量子力学的教科书和科普读物，几乎所有这些资料都给我们灌输了两个观点：量子力学告诉我们这个世界的底层是离散的；量子力学揭示出不确定性比确定性更加根本。虽然这两点并没有错，但是单凭这两点我们仍然无法判断量子力学作为一门数学相对于其他数学，例如离散数学和概率论的优势在哪。也就是说，这样一种普遍的观点完全没有抓住量子力学最终的根本所在。
笔者认为，量子力学的根本就蕴含在量子概率的运算法则之中，这套运算法则揭示出了另外一种被我们忽视的不确定性，这就是系统的属性依赖于观察者的观测作用的不确定性。为了更好的理解这种不确定性，让我们先用著名魔术师刘谦曾经在电视上表演的一个有趣的小魔术讲起。

图3-3 魔术师刘谦

有一次，刘谦表演猜数字的魔术。以前的猜数字魔术都是观众心中想一个数字，然后魔术师来猜。但是这次的魔术完全不一样，是刘谦先在心中想一个数字，并把它写在纸条上，然后反过来让观众来猜。比如某观众猜的数字是“5”，这个时候刘谦缓缓打开纸条让大家看，的确是数字5！再来一次，刘谦在纸上写好一个数字，另外一个观众猜“7”，打开一看，没错的确是7！刘谦号称，他能让观众具备“读心术”。

我虽然不知道刘谦的魔术是怎么变的，但是这个魔术的确像极了量子系统的行为。我们看到，这里面最让人费解的事情就在于刘谦写下数字的动作在前，观众猜数字的动作在后，而观众猜的数字具有很大的不确定性，所以刘谦之前猜出的数字应与观众之后说出的数字有很大的差异才对。可是，事实却是刘谦每次都能猜对。我们怎么解释呢？难道说因果规律反了？刘谦能够预测观众的未来？
其实有一种可能能很好的解释这个表面上的悖论，那就是刘谦之前根本没有在纸上写下任何字母，只有当观众说出他心目中的数字的时候，刘谦再用魔术的手法快速地在纸上写下观众说出的数字。
换句话说，也就是刘谦可以通过一张空白的纸条，来应付观众在动态的交互过程中的不确定性。这种不确定性就是我所说的交互的不确定性，也就是说系统的行为是完全依赖事后观察者对它的观察行为，它与传统概率所描述的不确定性是完全不同的。我认为，量子概率恰恰描述了这种交互性的不确定性！为了更好的理解量子概率和可交互的不确定性之间的关系，让我们从量子力学中最著名的双缝试验说起。

双缝试验与交互不确定性

图3-4 双缝干涉实验

这是一个经典的量子力学试验，假设O点是一个电子源能够源源不断地发射电子，电子经过AB屏的两个缝隙A和B后会发生干涉现象。从而在l屏上形成干涉条纹。我们可以减小O发射电子的强度，使得每次只能发射一个电子。这样，l屏上的干涉条纹就表示电子打到该点的概率。

假如我在A点处放一个探测电子是否经过A缝的仪器，只要我能读出电子是否已经经过了该点，这种测量行为就会直接干扰在C点发现电子的概率大小。如果电子是小球，我们知道这种观测行为是不会对小球到达C点的概率发生任何影响的。所以，量子力学所描述的对象具有交互不确定性。

为了更清楚地看出这种交互不确定性，让我们将双缝试验和之前所说的刘谦的魔术进行对比。假设刘谦的魔术仅仅限定在0和1两个数字之间。那么刘谦写下了一个数字在纸片上就相当于我们的粒子发射器发射出来一个电子。观众对这张纸上面的数字猜测是0还是1就相对在A,B屏的地方放置探测器考察粒子是经过了A还是经过了B。最后刘谦把纸条打开就相当于我们在l屏处观测电子，并且发现数字是0对应粒子达到了C点，是1则对应没达到。

如果观众不去猜纸条上的数字，刘谦直接打开纸条，就相当于我们不在AB屏的地方安置探测器，而直接观测C点的结果。如果观众猜纸条上的数字之后再去打开纸条就相当于我们从A,B处进行了一次观测之后再去考察电子飞到C点的情况。打开刘谦的纸条总能得到正确的结果是因为刘谦会利用魔术根据观众的观测，动态的更改纸条上的数字，同样在A点观测电子和不观测电子得到在C点完全不同的概率也是因为电子会根据观察者的观测行为动态地改变自身。

量子概率运算法则

为了使上面的讨论更加精确，让我们对量子概率运算法则进行一些简单的介绍。还是以双缝干涉实验的例子出发，我们先给出经典概率运算法则，之后再与量子概率运算法则进行对比。

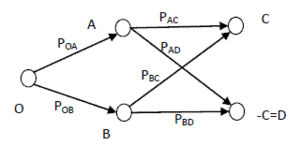
首先，我们可以把双缝试验改写成一个经典的马尔科夫链：

图3-5 描述粒子行为的马尔科夫链

设电子（经典粒子）从O点飞出，以P_OA的概率飞到A点或者以P_OB的概率飞到B点，然后再以概率P_AC飞到C点或者以P_AD的概率飞到不是C的点（我们暂且称之为D点）。那么，我们在C点发现电子的概率就应该是：

[math]\displaystyle{ P_{C} = P_{OA}P_{OC}+P_{OB}P_{BC} }[/math]　　　　　　(1)

假设电子可以源源不断地从O点飞出经过A或者B再打到C或者D点上。这个时候我们在A点放置一个探测器来测量电子到达A点的概率。

[math]\displaystyle{ P_{A} = P_{OA} }[/math]　　　　　　(2)

由于电子是经典粒子，所以观测电子的行为不会干扰最终在C点观测到电子的最终结果，因此电子到达C点的概率仍然是（1）式。
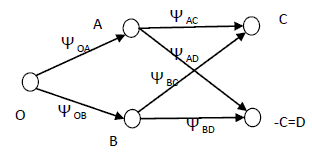
下面，我们进入了量子概率的世界（关于这部分运算，请参考《费曼物理学讲义3》和《量子计算和量子信息（一）》）。首先，对于电子量子的行为，我们仍然可以用类似的图形表示：

图3-6　　描述量子行为的复数概率图

与上图的不同之处就在于所有边上的条件概率都不再是一个[0,1]内的实数，而是一个复数，也就是这些条件“概率”可以写成复数的形式：

[math]\displaystyle{ \Psi = a +bi }[/math]　　　　　　　(3)

这些复数“概率”有一个学名叫做概率波振幅。你一定会好奇怪，为什么要写成复数呢？a和b分别表示什么意思？i又表示什么意思？对不起，估计没有人知道这个问题的答案，这恰恰就是量子力学困惑那么多物理、数学大师的地方所在。不管怎么样，物理学家告诉我们，只要你假设电子的概率可以取复数，那么概率的那些运算法则对概率波振幅都成立。比如，我们可以计算出电子到达C点的概率波振幅：

[math]\displaystyle{ \Psi_{C}=\Psi_{OA}\Psi_{AC}+\Psi_{OB}\Psi_{BC} }[/math]　　　　　　　(4)

量子力学还告诉我们，这个概率波振幅虽然满足概率运算的一切法则，可我们并不能直接观测到它，而只能间接地通过概率推测出它来。也就是说，我们在C点观测电子的概率是C点概率波振幅这个复数的模的平方，即：

[math]\displaystyle{ P_{C} = \mid \Psi_{C}\mid ^{2} }[/math]　　　　　　　(5)

让我们再来考虑在A点对电子的观测行为。首先，我们在A点观测到电子的概率是：

[math]\displaystyle{ P_{A} = \mid \Psi_{OA}\mid ^{2} }[/math]　　　　　　　(6)

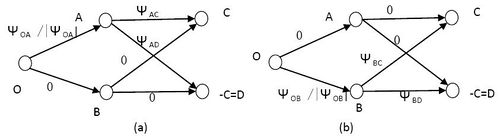
其次，量子力学还告诉我们，一旦我们知道了电子到达A点的概率，电子的状态就会发生严重的扭曲变形（也就是观测行为会影响电子的状态），使得电子在整个行程中的状态都会发生变化。当在A点观测到电子的时候（概率是P_A），概率图转变成(a)的情况，当在B点（概率是P_B）观测到电子的时候概率图变成(b)的情况。

图3-7 观测后的两张图

这样，综合(a)、(b)两种情况，只要在A,B发生测量，那么在C点观测到电子的概率就变为：

[math]\displaystyle{ P_{C} =P_{A}\frac{\mid \Psi_{OA}\Psi_{AC}\mid ^{2}}{\mid \Psi_{OA}\mid ^{2}}+P_{B}\frac{\mid \Psi_{OB}\Psi_{BC}\mid ^{2}}{\mid \Psi_{OA}\mid ^{2}}=\mid \Psi_{OA}\Psi_{AC}\mid ^{2}+\mid \Psi_{OB}\Psi_{BC}\mid ^{2} }[/math]　　　　　　　(7)

这样，对于任意的四个复数[math]\displaystyle{ \Psi_{OA},\Psi_{OB},\Psi_{AC},\Psi_{AB} }[/math]有：

[math]\displaystyle{ P_{C} =\mid \Psi_{OA}\Psi_{AC}+ \Psi_{OB}\Psi_{BC}\mid ^{2}\neq \mid \Psi_{OA}\Psi_{AC}\mid ^{2}+\mid \Psi_{OB}\Psi_{BC}\mid ^{2}=P_{C}' }[/math]　　　(8)

所以在中间AB屏测量电子的行为会严重干扰最终在C点测量粒子的概率。
为了让我们对这种复数的运算有更清晰、直观的认识，让我们来考察一种特殊的情况，即让AC和BC的概率波振幅相等：

[math]\displaystyle{ \Psi_{OA} = r_{1}(Cos\alpha +iSin\alpha)\lt br\gt \Psi_{OB} = r_{2}(Cos\beta +iSin\beta)\lt br\gt \Psi_{AC} = \Psi_{BC} = R(Cos\theta +iSin\theta) }[/math]　　　　　(9)

这样，我们可以计算得到：

[math]\displaystyle{ P_{C} =\mid \Psi_{OA}\Psi_{AC}+ \Psi_{OB}\Psi_{BC}\mid ^{2}=R^{2}(\mid \Psi_{OA}\mid^{2}+\mid \Psi_{OB}\mid^{2}+(\Psi_{OA}\Psi_{OB}^{*}+\Psi_{OB}\Psi_{OA}^{*}))=R^{2}(r_{1}^{2}+r_{2}^{2}+2r_{1}r_{2}Cos(\alpha-\beta)) }[/math]　　　　　　(10)

其中*表示复数的共轭运算，而：

[math]\displaystyle{ P_{C}' = \mid \Psi_{OA}\Psi_{AC}\mid ^{2}+\mid \Psi_{OB}\Psi_{BC}\mid ^{2} = R^{2}(r_{1}^{2}+r_{2}^{2}) }[/math]　　　　　(11)

比较这两个式子，我们发现，关键的因素就在于P_C和P_C’相差一个项：

[math]\displaystyle{ 2r_{1}r_{2}Cos(\alpha-\beta)) }[/math]　　　　　　(12)

这一项在量子力学中称为相干项，也就是互斥的两条路径[math]\displaystyle{ O\rightarrow A }[/math]和[math]\displaystyle{ O\rightarrow B }[/math]会发生相互干涉，使得最后的测量结果发生偏差。我们知道由于Cos函数可以取正值或者负值，所以最终的P_C有可能大于P_C’也有可能小于它。

量子测量理论

以上，我们把概率的运算全部复数化就得出了量子概率的计算结果，这种计算结果反映出一种观察者的测量作用对系统本身的干扰作用。冯.诺伊曼为量子力学建立数学基础（参见von Neumann 著《Mathematical foundations of quantum mechanics》）的过程中采用了略为不同的方法。首先，冯.诺伊曼没有定义一种关于复数的概率运算法则（事实上，上面讲述的复数概率运算思路属于物理学家费曼的路径积分法），而是扩充了系统的状态、事件以及事件运算法则等概念，也能得到和我们一模一样的结果。

但是，在冯诺伊曼的体系中，他明确提出来了一种测量运算的概念。所谓的一次测量就是指希尔伯特空间上的一个厄米(Hermite)矩阵，将这个矩阵作用到系统的状态上便能得到系统测量完后的结果，并且也能得出观察者所能得到的事件的概率。

与我们上面所说的可交互性不确定性解释不同，冯诺伊曼的解释更偏向电子在被测量之前根本就不是一个电子，而是一种充满着各种可能性的概率波，在被测量的一瞬间，这个概率波才从一个可能状态转变成了一种观察者已知的确定状态。换句话说，电子在被测量之前根本就不存在！一切关于电子的状态信息都是我们观测到的结果。

J.A. Wheeler曾经在他的著作《Quantum Theory and Measurement》中提到了一个非常有趣的21问游戏的例子来说明量子测量理论。

---

所谓的21问游戏是这样的：我随便想象一个人，然后你可以问我任意的问题，但是我的回答只能用“是”和“否”。比如我想好的人是希特勒。咱俩的对话如下：
　　你：这个人还活着吗？
　　我：否
　　你：他是男的吗？
　　我：是
　　你：他是中国人吗？
　　我：否
　　……
　　你：他是希特勒吗？
　　我：是
　　就这样，如果你能够通过问21个问题而猜出最后的答案，那么你就赢得了游戏。

---

在经典的概率世界中，我想好的人是一个确定的人。但是在量子的世界中，我开始并没有想好一个真正的人，也就是说那个人一开始并不存在。然后，你开始问一系列问题，我用一串随机的是和否来回答你，但是要保证前后回答的逻辑连贯一致性。当一串问题问下来，虽然我的头脑中开始的那个人物并不存在，但是由于我的回答需要保持逻辑连贯性，因此我的看起来随机的回答就会被你的问题本身而塑造、确定。最终，我很有可能被你问出来一个希特勒！

在这个小游戏中，每一个问题就相当于一次量子测量，所谓的真实答案并不是一个客观存在的预设，而是不断被这一次次的测量塑造而成的。

走向宏观世界

也许大多数人对于刚才所述的量子的古怪行为还算能接受，因为那毕竟发生在离我们非常遥远的微观世界中。然而，我写这篇文章的一个主要目的就在于将量子力学应用于宏观系统之中。我认为，我们身处的复杂系统到处存在着观察者的测量与被观测系统相互耦合的情况。

比如，J. R. Busemeyer 和Z. Wang就发现人类的决策就是一种类量子行为（请参看这个PPT），即可以用量子概率描述的宏观系统。他们设计了一组人类行为学试验，让人类被试作出类似电子的决策。

首先，他们让每个人类被试观察下列一组头像图片：

图3-8 Busemeyer和Wang的试验

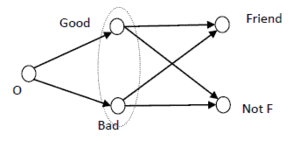
然后让被试在两组不同的实验条件下完成判断：是否会把这个人当做自己的朋友。在第一组实验中，试验者要求被试直接作出判断，会不会把这张脸当作自己的朋友。第二组试验则要求被试先把所有的脸归为两类：好人或者坏人，然后再根据这个归类的结果判断是否把这人当作自己的朋友。我们看到，这个试验很像电子经过双缝的试验，如图所示：

图3-9 人类被试的决策行为

被试的选择行为就相当于电子通过双缝的行为。试验员询问被试的问题就相当于对被试进行测量。第一组试验要求被试直接做出朋友或者不是朋友的选择就相当于在最后一个屏的地方测量电子，而不管被试是把这张脸分类成好人还是坏人。假设在这种情况下针对某一张脸测得是朋友的概率是P(F)。

在第二组情况下，试验员相当于进行了两次连续的测量，首先让被试做出分类为好人还是坏人的测量，之后再作出是否把此人当作朋友的测量，在这种情况下测得的朋友概率是P’(F)。

假如人类的决策是按照经典概率运算的法则，那么P(F)就应该等于P’(F)。但是J. R. Busemeyer 和Z. Wang却发现试验结果是P(F)>P’(F)。

假如按照量子概率法则对人类的决策行为却得出了很好的解释，这说明，我们完全有可能用量子概率的运算法则描述宏观的人类决策行为(参考此文)。

实际上，近年来把量子理论应用研究各种各样的复杂系统中的工作越来越多（参见Quantum Interaction的论文集）。还有相当多的学者研究如何将量子概率理论应用于复杂金融系统中，参见：《Quantum Finance》以及：《金融物理学》。

统计物理的精髓：观察者的信息

量子物理通过测量把隐藏在幕后的观察者搬到了前台，这是毋庸置疑的。但是，当我说统计物理其实也隐藏着对观察者测量作用的描述的时候，恐怕很多读者就会不同意了。实际上，我们将会看到，统计物理学之父——玻尔兹曼的一个最大的贡献就在于他发明了基于观察者的粗粒化方法，从而最终发现了观察者测量作用的一个非常重要的结果：忽略信息。

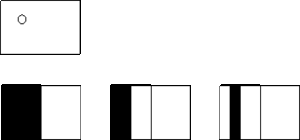
在这里，我们不对统计物理的细节进行过多说明，感兴趣的读者请参看我曾经写过的科普文章：生命之流(5)——连接上帝的纽带-熵 。我只是想引起大家注意的是，玻尔兹曼为了推导出气体分子的速度分布规律，引入了一种被后来称之为粗粒化方法（Coarse graining）的操作。如下面的两幅图所示：

图3-10 气体的微观态

如图，假如有6个小球分布在若干容器里（有3种状态）。由于我们观测系统的试验仪器分辨率很粗糙，不能精确的定位每一个小球处在哪一个小格子里。所以，我们只能观察到有多少个球在容器的黑线左边，多少个小球在黑线右边，所以只能得到如下图所示的三种对应的宏观状态：

图3-11 气体的宏观态

显然，通过宏观态，我们就能够得到对系统更加粗糙的描述，因此这样一种从微观过渡到宏观的过程也被称之为粗粒化过程。玻尔兹曼在讨论这样一种粗粒化过程的时候完全没有提观察者的事儿，但我们现在知道，其实这种从微观到宏观的过度就是观察者选择了不同的尺度来观察系统，而得到的不同描述恰恰正是观察者测量之后所获得的信息。

在以往对统计物理的解释中，观测被称之为一种忽略信息的过程（参见：生命之流(5)——连接上帝的纽带-熵）。然而这种信息忽略的说法似乎并不准确，因为按照我们现在对观察的理解，整个世界完全是由观察者观测出来的结果，也就是说原则上来讲并不存在着微观态，那不过是我们捏造出来一种说法而已，所以得到的宏观态并不能说是一种忽略信息的结果，而应该纯粹看作是观察者进行信息获取的结果。统计物理的成功向我们展示了：正是这样一种信息的获取过程却能推导出整个宏观热力学的很多结果。

从强力法则到标度不变性

近些年来越来越多的人把统计物理用于研究各式各样的复杂系统中，并发现了一些普适的规律。例如，经济系统中，如果把一个人所拥有的财富量记作x，拥有这么多财富量的人数记作p(x)，那么实证数据表明p(x)~x^-1.5，这被称之为帕累托律（Pareto Law）。在一本英文书中，如果把某一个单词w出现的次数记为f(w)，将所有出现过的单词按照f值的大小排序，记r(w)为该单词w在排序中的序数，那么f(w)~r(w)^-1，即w出现的频率与它的排序r呈反比，这被称之为Zipf律。还有城市的人口，地震的规模都呈现相似的分布特征，这被称之为幂律现象（Power law）。根据这个英文名，我则戏称这个法则为强力法则。

之所以称这些规律为强力法则，更主要的原因是这种现象在复杂系统中的普适性，从细胞生物体，到互联网，再到人际交往关系，幂律现象比比皆是（有关幂律的讨论，请参看计算士的科普文章：涌现4）。

进一步，人们发现，这些普遍存在的幂律现象背后有一种更深层次的普适规律，也就是标度不变性。为了解释这种标度不变性，让我们用分形的例子来说明：

图3-12 分形图案

观察者将观察的精度提高的过程就是从左图过渡到右图的过程，我们知道，当观察者的观测精度扩大9倍，那么它就能看到每一个黑色方格之内的细节，因此也就有了右图。我们说这个图形是标度不变的，也就是说在扩大9倍的图中，每一个1/9方格的内容都与原来的图一样。这样一种对原始图形不断放大的方法在物理中被称为重正化操作(Renormalization)。由此，我们看出，真实的复杂系统恰恰具有一种明显地依赖于观察者的行为，这就是：标度不变性，即系统不会随着我们观察者观察它的尺度而变化(参看科普小文：分形与尺度相对论)。

测量——联系空间标度和时间的纽带

为了更清楚地看出从观察者的角度出发来重新审视各种物理问题的重要性，让我们考察另外一个例子。

图3-13 对电子位置的测量

假设容器中有一个电子，我们想知道这个电子所在的精确位置。于是我们展开对电子的测量。第一次测量的时候，由于我们测量的精度非常粗糙，我们只能判断出电子在容器中心的左侧还是右侧，假如我们知道电子是在左侧；第二次，我们可以提高测量的精度了，从而精确到容器尺度的1/4。因为我们已经知道了电子在左侧，所以我们再对左侧的这个方格进行一次更精确的测量，假设这次电子仍然在左侧的1/4方格中。第三次，我们用更高的精度测量电子的位置，得到电子在右侧的1/8方格中，这个过程还可以无限延伸下去……。
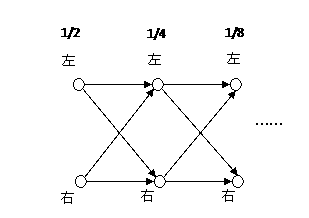
不难想象，这样一个采用不同精度对电子位置的测量过程可以用下图表示：

这张图表示在不同的尺度下对粒子所在位置进行测量。在1/2尺度下，询问粒子是在左侧还是在右侧，在1/4尺度下再次询问粒子在左侧还是右侧。其中箭头的方向表示测量所蕴含的因果方向，也就是如果我在1/2尺度下测量知道粒子在左侧，那就意味着该格子在1/4尺度下测量粒子要么在左侧要么在右侧。

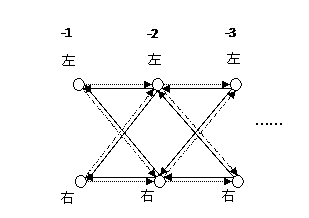
我们可以考虑一个类似的在时间上进行的电子双缝试验，如下图：

假设电子经过一系列装有双缝的屏幕从右侧飞向左侧。观察者从左侧往右侧测量，也就是说，观察者先要确认在最左侧的一步电子经过了左侧的缝隙还是右侧的缝隙；然后在获得了消息之后，再询问电子上一时刻是飞过了左缝还是右缝，然后再询问……。图中的实箭头表示电子的“运动方向”（根据量子力学，电子应没有运动轨迹，箭头仅仅为了表示方便），图中的虚箭头则表示观察者询问问题的方向。比较这两张图我们发现，他们在观测的结构上是完全等价的。

也就是说，在空间不同标度上对电子位置的测量完全等价于在不同时刻对一个电子经过若干双缝的情况进行测量。同时，我们还应注意到一个非常重要的事实：时间等价于观测标度的对数（参加两幅图上面在不同节点的数字标注）。

一旦我们将这两种描述联系起来，我们将有可能建立起量子概率和分形几何之间的深刻联系，从而可以互相借鉴对方的工具。比如，分形中的标度不变性就对应了在时间上测量的不变性。根据量子力学我们知道，任何一种时空上的对称性结构就对应了一种守恒性。所以，时间对称性结构自然会要求能量守恒。而我们看到了标度不变性与时间不变性的关系，那么也就意味着我们可以在标度的变换中找到某种守恒量，也许这种量可以称之为标度的哈密顿量，它在任何一种标度中都是守恒的。

总之，我们可以把量子测量理论中的很多概念平移到空间尺度的测量中，这就可能为复杂系统建立一套基于观察者的测量理论。

通过上面的论述，我们已经学会用一种从科学的背景——观察者的角度出发来看待现代物理学的本领。渐渐地发现，如果放弃真实不变的世界的说法，我们不仅得不出任何自相矛盾的结果，反而得出了对这个世界更加简洁而深刻的描述：观察者无论在时间还是空间上去测量，都会得出相似的结论（标度不变性和时间不变性）。

熵——对观测自身的测量

刚才的讨论仅仅局限在观察者对外在世界的测量，其实观察者还会对自身构建的世界进行测量。回想图2-2，输入给测量的信息不仅来自于非我的外界，还来自于我的内部世界。从内部世界的角度说，一次观测可以表示成下图：

单从观察者的角度看来，一次测量过程不仅仅是把所谓的“真实”映射为他头脑中的真相，而且也是观察者“任意创造”出来的可能性世界到真实观察世界的一次映射过程。如上图所示。这张图刚好描述了图2-2中从“我”这里输入给观察的信息。也就是说，在一次真正的观测之前，观察者的头脑中闪现出各种各样的可能想象。而一旦作出观察之后，所有的想象都灰飞烟灭了，最后只能塌缩成一种可能性，即观察者感受到的真实。这种从可能世界到真实世界的转化过程恰好跟重要的物理学量：熵，联系到了一起（参看生命之流(5)——连接上帝的纽带-熵）。

我们不就具体计算进行过多讨论，而只做出定性上的说明。观察者头脑中的可能世界决定了观察者会怎样进行测量得到有效的信息。可能性的世界越大，观察者就会寻问越多的问题。假设观察者在每次测量中都询问系统一个是否的问题，从而得到反馈的测量结果，那么，熵就对应了这些有效测量的次数。

从时间的角度来看，如果观察者的测量结果没有发生任何改变，那么熵也不会发生变化。所以，熵的变化与测量结果的变化深深地联系了起来。按照客观时间的观点（即存在着一个客观流逝的时间），时间上的每一次测量并不一定返回完全不同的结果，所以熵的变化也是不均匀的。但是，从观察者的角度来说，只有测量结果的变化才是真实的，所以熵增恰恰反映了一种真实的变化。也就是说，在观察者看来，熵的均匀变化定义了一种主观时间。

熵其实可以看作是观察者对自身测量结果的一种测量。也就是，熵的变化衡量了观察者的一系列测量动作的效率。也正因为此，熵这个物理量具有很强的自指性。

小结与展望

本章站在观察者的角度重新看待现代物理学的两大分支：量子力学和统计力学。我们发现，与其说这两套学说是在发现客观世界的一些本质规律，还不如说它们发现的是观察者观测世界的各种现象和规律。
量子力学已经把观察者的观测行为作为一个明确的假设放到了整个力学框架范围内，而统计物理中最重要的两个概念：标度不变性和熵也刚好是在描述观察者的观测行为。所以，采用观察者的视角来重新看待整个现代物理是再合适不过的。

当然，物理学的分支还相当庞杂，但是几乎所有的物理理论的根源都可以归结为某种观察者效应。例如，相对论中的相对性原理可以归结为观察者在不同的运动参照系下考察物理规律的不变性；力学中的各种对称性（空间对称、时间对称、旋转对称）都可以看作是观察者对于对称的偏好等等。

然而，物理学自从发现了量子力学以来就开始变得与众不同了。原因在于，观察者作为一个显式的因素被放到了理论框架中来。在此之上，量子场论以及量子引力等理论又进一步发展了量子力学。从观察者的角度来看，笔者认为这些更深层次的学科的意义也就在于进一步放松客观世界的假定。在量子力学中，虽然电子在被测量到之前已经不被视为一种客观实在的粒子，但是，毕竟我们还需要一个客观的波函数来描述电子的状态。我认为，到了量子场论的地步，即使波函数也会进一步消失，我们完全没有必要假设有一个客观存在的对应着电子的波，因为场论中涵盖了粒子的生灭过程。也许到了量子引力和终极理论那里，客观世界唯一的影子也不需要存在了，最终物理学将证明，一切都源于虚无。

然而，本人毕竟不是搞物理的，我也对这些进一步的物理问题兴趣不大，但是，我确信观察者理论对于这些问题具有一定的独特性和穿透性。希望对此理论感兴趣的朋友能够将其在物理学中的应用发扬光大。

相关页面

• 系统中的观察者(1)——引言
• 系统中的观察者(2)——基本框架
• 系统中的观察者(4)——人工智能的观察者
• 系统中的观察者(5)——自指
• 系统中的观察者(6)——互联网与观察之流

---

本中文词条由Jake编写，薄荷编辑，欢迎在讨论页面留言。

本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。