系统动力学

此词条暂由彩云小译翻译，未经人工整理和审校，带来阅读不便，请见谅。

Dynamic stock and flow diagram of model New product adoption (model from article by John Sterman 2001)新产品采用模式的动态库存和流程图（模式来自文章John Sterman 2001）

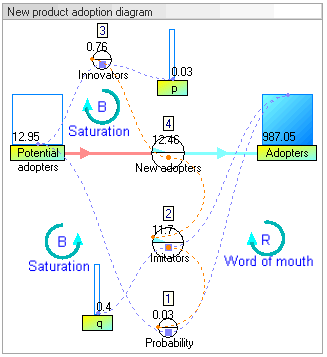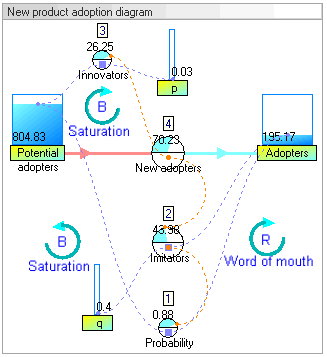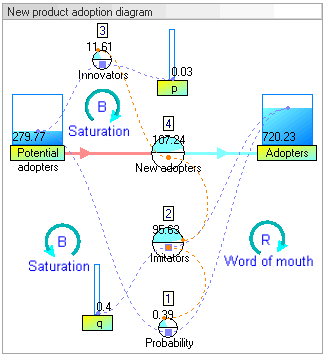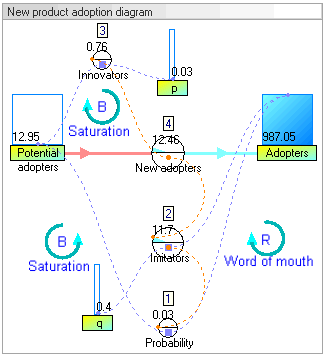
Dynamic stock and flow diagram of model New product adoption (model from article by John Sterman 2001)

新产品采用模式的动态库存和流程图(模式来自文章[ John Sterman 2001]])

System dynamics (SD) is an approach to understanding the nonlinear behaviour of complex systems over time using stocks, flows, internal feedback loops, table functions and time delays.

System dynamics (SD) is an approach to understanding the nonlinear behaviour of complex systems over time using stocks, flows, internal feedback loops, table functions and time delays.

系统动力学 System Dynamics，SD是利用存量、流量、内部反馈回路、表函数和时滞等信息来理解复杂系统随时间变化的非线性行为的一种方法。

概览 Overview

System dynamics is a methodology and mathematical modeling technique to frame, understand, and discuss complex issues and problems. Originally developed in the 1950s to help corporate managers improve their understanding of industrial processes, SD is currently being used throughout the public and private sector for policy analysis and design.

System dynamics is a methodology and mathematical modeling technique to frame, understand, and discuss complex issues and problems. Originally developed in the 1950s to help corporate managers improve their understanding of industrial processes, SD is currently being used throughout the public and private sector for policy analysis and design.

系统动力学是构建、理解和讨论复杂问题的一种方法论和数学建模技术。这一领域最初是在20世纪50年代发展起来的，目的是帮助企业管理者提高对工业过程的理解，现在被公共和私营部门用于政策分析和设计问题上。

Convenient graphical user interface (GUI) system dynamics software developed into user friendly versions by the 1990s and have been applied to diverse systems. SD models solve the problem of simultaneity (mutual causation) by updating all variables in small time increments with positive and negative feedbacks and time delays structuring the interactions and control. The best known SD model is probably the 1972 The Limits to Growth. This model forecast that exponential growth of population and capital, with finite resource sources and sinks and perception delays, would lead to economic collapse during the 21st century under a wide variety of growth scenarios.

Convenient graphical user interface (GUI) system dynamics software developed into user friendly versions by the 1990s and have been applied to diverse systems. SD models solve the problem of simultaneity (mutual causation) by updating all variables in small time increments with positive and negative feedbacks and time delays structuring the interactions and control. The best known SD model is probably the 1972 The Limits to Growth. This model forecast that exponential growth of population and capital, with finite resource sources and sinks and perception delays, would lead to economic collapse during the 21st century under a wide variety of growth scenarios.

20世纪90年代推出了更方便用户使用的版本——具有图形用户界面 GUI系统动力学软件，并应用于各种系统。SD模型通过以小时间增量更新所有变量，用正反馈和负反馈以及时间延迟来构造交互和控制，从而解决了同时性（互为因果）的问题。最著名的SD模型可能是1972年的”增长极限“模型。该模型预测，随着人口和资本的指数增长，在有限的资源和汇以及感知延迟的情况下，将导致21世纪各种增长情景下的经济崩溃。

System dynamics is an aspect of systems theory as a method to understand the dynamic behavior of complex systems. The basis of the method is the recognition that the structure of any system, the many circular, interlocking, sometimes time-delayed relationships among its components, is often just as important in determining its behavior as the individual components themselves. Examples are chaos theory and social dynamics. It is also claimed that because there are often properties-of-the-whole which cannot be found among the properties-of-the-elements, in some cases the behavior of the whole cannot be explained in terms of the behavior of the parts.

System dynamics is an aspect of systems theory as a method to understand the dynamic behavior of complex systems. The basis of the method is the recognition that the structure of any system, the many circular, interlocking, sometimes time-delayed relationships among its components, is often just as important in determining its behavior as the individual components themselves. Examples are chaos theory and social dynamics. It is also claimed that because there are often properties-of-the-whole which cannot be found among the properties-of-the-elements, in some cases the behavior of the whole cannot be explained in terms of the behavior of the parts.

系统动力学是系统理论的一个方面，是理解复杂系统动态行为的一种方法。该方法的基础是认识到，任何系统的结构，其组成部分之间的许多循环的、互锁的、有时是时间延迟的关系，在决定其行为方面往往与单个组件本身一样重要。例如混沌理论和社会动力学。它还声称，由于在元素的属性中往往存在无法找到的整体属性，在某些情况下，整体的行为不能用部分的行为来解释。

历史 History

System dynamics was created during the mid-1950s by Professor Jay Forrester of the Massachusetts Institute of Technology. In 1956, Forrester accepted a professorship in the newly formed MIT Sloan School of Management. His initial goal was to determine how his background in science and engineering could be brought to bear, in some useful way, on the core issues that determine the success or failure of corporations. Forrester's insights into the common foundations that underlie engineering, which led to the creation of system dynamics, were triggered, to a large degree, by his involvement with managers at General Electric (GE) during the mid-1950s. At that time, the managers at GE were perplexed because employment at their appliance plants in Kentucky exhibited a significant three-year cycle. The business cycle was judged to be an insufficient explanation for the employment instability. From hand simulations (or calculations) of the stock-flow-feedback structure of the GE plants, which included the existing corporate decision-making structure for hiring and layoffs, Forrester was able to show how the instability in GE employment was due to the internal structure of the firm and not to an external force such as the business cycle. These hand simulations were the start of the field of system dynamics.

System dynamics was created during the mid-1950s by Professor Jay Forrester of the Massachusetts Institute of Technology. In 1956, Forrester accepted a professorship in the newly formed MIT Sloan School of Management. His initial goal was to determine how his background in science and engineering could be brought to bear, in some useful way, on the core issues that determine the success or failure of corporations. Forrester's insights into the common foundations that underlie engineering, which led to the creation of system dynamics, were triggered, to a large degree, by his involvement with managers at General Electric (GE) during the mid-1950s. At that time, the managers at GE were perplexed because employment at their appliance plants in Kentucky exhibited a significant three-year cycle. The business cycle was judged to be an insufficient explanation for the employment instability. From hand simulations (or calculations) of the stock-flow-feedback structure of the GE plants, which included the existing corporate decision-making structure for hiring and layoffs, Forrester was able to show how the instability in GE employment was due to the internal structure of the firm and not to an external force such as the business cycle. These hand simulations were the start of the field of system dynamics.

系统动力学是在20世纪50年代中期由麻省理工学院的 Jay Forrester 教授创立的。1956年，Forrester 接受了新成立的 MIT斯隆管理学院授予的教授职位。他最初的目标是确定如何利用他在科学和工程方面的背景，以某种有用的方式，在决定企业成败的核心问题上发挥作用。Jay Forrester 对工程学背后的共同基础的洞察，导致了系统动力学的产生，在很大程度上，是由于他在20世纪50年代中期与通用电气 General Electric，GE的经理们的合作而触发的。当时，通用电气的经理们感到困惑，因为很明显肯塔基州电器厂的就业周期为三年。商业周期被认为不足以解释就业的不稳定性。通过手工模拟（或计算）通用电气工厂的股票流量反馈结构，包括现有的企业决策结构的雇用和裁员，Forrester 能够显示通用电气就业的不稳定性是由于公司的内部结构，而不是由于商业周期等外部力量。这些手工仿真是系统动力学领域的开端。

During the late 1950s and early 1960s, Forrester and a team of graduate students moved the emerging field of system dynamics from the hand-simulation stage to the formal computer modeling stage. Richard Bennett created the first system dynamics computer modeling language called SIMPLE (Simulation of Industrial Management Problems with Lots of Equations) in the spring of 1958. In 1959, Phyllis Fox and Alexander Pugh wrote the first version of

During the late 1950s and early 1960s, Forrester and a team of graduate students moved the emerging field of system dynamics from the hand-simulation stage to the formal computer modeling stage. Richard Bennett created the first system dynamics computer modeling language called SIMPLE (Simulation of Industrial Management Problems with Lots of Equations) in the spring of 1958. In 1959, Phyllis Fox and Alexander Pugh wrote the first version of

在20世纪50年代末和60年代初，Forrester 和一个研究生团队将系统动力学的新兴领域从手工仿真阶段转移到正式的计算机建模阶段。1958年春天，Richard Bennett 创造了第一个系统动力学计算机建模语言，叫做 SIMPLE (用大量方程模拟工业管理问题)。1959年，菲利斯 · 福克斯和亚历山大 · 普撰写了第一个版本的

DYNAMO (DYNAmic MOdels), an improved version of SIMPLE, and the system dynamics language became the industry standard for over thirty years. Forrester published the first, and still classic, book in the field titled Industrial Dynamics in 1961.

DYNAMO (DYNAmic MOdels), an improved version of SIMPLE, and the system dynamics language became the industry standard for over thirty years. Forrester published the first, and still classic, book in the field titled Industrial Dynamics in 1961.

Dynamo (DYNAmic MOdels)是 SIMPLE 的改进版本，系统动力学语言成为行业标准已有三十多年。1961年，弗雷斯特出版了第一本至今仍然是经典的著作《工业动力学》。

From the late 1950s to the late 1960s, system dynamics was applied almost exclusively to corporate/managerial problems. In 1968, however, an unexpected occurrence caused the field to broaden beyond corporate modeling. John F. Collins, the former mayor of Boston, was appointed a visiting professor of Urban Affairs at MIT. The result of the Collins-Forrester collaboration was a book titled Urban Dynamics. The Urban Dynamics model presented in the book was the first major non-corporate application of system dynamics.

From the late 1950s to the late 1960s, system dynamics was applied almost exclusively to corporate/managerial problems. In 1968, however, an unexpected occurrence caused the field to broaden beyond corporate modeling. John F. Collins, the former mayor of Boston, was appointed a visiting professor of Urban Affairs at MIT. The result of the Collins-Forrester collaboration was a book titled Urban Dynamics. The Urban Dynamics model presented in the book was the first major non-corporate application of system dynamics.

从1950年代后期到1960年代后期，系统动力学几乎完全适用于公司 / 管理问题。然而，在1968年，一个意想不到的事件使这个领域的范围扩大到公司模型之外。波士顿前市长约翰 · f · 柯林斯被任命为麻省理工学院城市事务的客座教授。柯林斯-福斯特合作的成果是出版了一本名为《城市动力学》的书。本书中提出的城市动力学模型是系统动力学的第一个主要的非企业应用。

The second major noncorporate application of system dynamics came shortly after the first. In 1970, Jay Forrester was invited by the Club of Rome to a meeting in Bern, Switzerland. The Club of Rome is an organization devoted to solving what its members describe as the "predicament of mankind"—that is, the global crisis that may appear sometime in the future, due to the demands being placed on the Earth's carrying capacity (its sources of renewable and nonrenewable resources and its sinks for the disposal of pollutants) by the world's exponentially growing population. At the Bern meeting, Forrester was asked if system dynamics could be used to address the predicament of mankind. His answer, of course, was that it could. On the plane back from the Bern meeting, Forrester created the first draft of a system dynamics model of the world's socioeconomic system. He called this model WORLD1. Upon his return to the United States, Forrester refined WORLD1 in preparation for a visit to MIT by members of the Club of Rome. Forrester called the refined version of the model WORLD2. Forrester published WORLD2 in a book titled World Dynamics.

The second major noncorporate application of system dynamics came shortly after the first. In 1970, Jay Forrester was invited by the Club of Rome to a meeting in Bern, Switzerland. The Club of Rome is an organization devoted to solving what its members describe as the "predicament of mankind"—that is, the global crisis that may appear sometime in the future, due to the demands being placed on the Earth's carrying capacity (its sources of renewable and nonrenewable resources and its sinks for the disposal of pollutants) by the world's exponentially growing population. At the Bern meeting, Forrester was asked if system dynamics could be used to address the predicament of mankind. His answer, of course, was that it could. On the plane back from the Bern meeting, Forrester created the first draft of a system dynamics model of the world's socioeconomic system. He called this model WORLD1. Upon his return to the United States, Forrester refined WORLD1 in preparation for a visit to MIT by members of the Club of Rome. Forrester called the refined version of the model WORLD2. Forrester published WORLD2 in a book titled World Dynamics.

系统动力学的第二个主要的非公司应用紧随第一个之后。1970年，Jay Forrester 应罗马俱乐部的邀请参加了在瑞士伯尔尼举行的一次会议。罗马俱乐部是一个致力于解决其成员所描述的”人类困境”的组织，即今后某个时候可能出现的全球危机，因为世界人口呈指数增长，对地球的承载能力(可再生和不可再生资源的来源及其处理污染物的汇)提出了要求。在伯尔尼会议上，Forrester 被问及是否可以用系统动力学来解决人类的困境。当然，他的回答是可以。在从伯尔尼会议回来的飞机上，弗雷斯特创建了世界社会经济系统系统动力学模型的初稿。他把这个模型叫做 WORLD1。回到美国后，弗雷斯特精炼了 WORLD1，为罗马俱乐部成员访问麻省理工学院做准备。称这个模型为 WORLD2的改进版本。在一本名为《世界动力学》的书中出版了 WORLD2。

Topics in systems dynamics

系统动力学主题

The elements of system dynamics diagrams are feedback, accumulation of flows into stocks and time delays.

The elements of system dynamics diagrams are feedback, accumulation of flows into stocks and time delays.

系统动力学图表的元素是反馈，流入库存的积累和时间延迟。

As an illustration of the use of system dynamics, imagine an organisation that plans to introduce an innovative new durable consumer product. The organisation needs to understand the possible market dynamics in order to design marketing and production plans.

As an illustration of the use of system dynamics, imagine an organisation that plans to introduce an innovative new durable consumer product. The organisation needs to understand the possible market dynamics in order to design marketing and production plans.

为了说明系统动力学的应用，设想一个组织计划推出一种创新的新型耐用消费品。组织需要了解可能的市场动态，以便设计市场营销和生产计划。

Causal loop diagrams

因果循环图

In the system dynamics methodology, a problem or a system (e.g., ecosystem, political system or mechanical system) may be represented as a causal loop diagram. A causal loop diagram is a simple map of a system with all its constituent components and their interactions. By capturing interactions and consequently the feedback loops (see figure below), a causal loop diagram reveals the structure of a system. By understanding the structure of a system, it becomes possible to ascertain a system’s behavior over a certain time period.

In the system dynamics methodology, a problem or a system (e.g., ecosystem, political system or mechanical system) may be represented as a causal loop diagram. A causal loop diagram is a simple map of a system with all its constituent components and their interactions. By capturing interactions and consequently the feedback loops (see figure below), a causal loop diagram reveals the structure of a system. By understanding the structure of a system, it becomes possible to ascertain a system’s behavior over a certain time period.

在系统动力学方法论中，一个问题或一个系统(例如，生态系统、政治系统或机械系统)可以表示为一个环路图。环路图是一个系统的简单映射，包含了系统的所有组成部分及其相互作用。通过捕捉相互作用和随之而来的反馈回路(见下图) ，环路图揭示了一个系统的结构。通过了解一个系统的结构，就有可能确定一个系统在一定时间段内的行为。

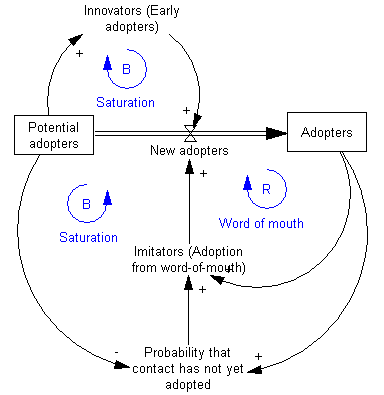
The causal loop diagram of the new product introduction may look as follows:

The causal loop diagram of the new product introduction may look as follows:

新产品介绍的环路图如下:

文件:Adoption CLD.svg

Causal loop diagram of New product adoption model

frame

框架

There are two feedback loops in this diagram. The positive reinforcement (labeled R) loop on the right indicates that the more people have already adopted the new product, the stronger the word-of-mouth impact. There will be more references to the product, more demonstrations, and more reviews. This positive feedback should generate sales that continue to grow.

There are two feedback loops in this diagram. The positive reinforcement (labeled R) loop on the right indicates that the more people have already adopted the new product, the stronger the word-of-mouth impact. There will be more references to the product, more demonstrations, and more reviews. This positive feedback should generate sales that continue to grow.

在这个图表中有两个反馈循环。右侧的正强化(标记为 r)循环表明，越多的人已经接受了新产品，口碑的影响就越强。将会有更多的产品参考，更多的演示和更多的评论。这种积极的反馈应该会产生持续增长的销售额。

The second feedback loop on the left is negative reinforcement (or "balancing" and hence labeled B). Clearly, growth cannot continue forever, because as more and more people adopt, there remain fewer and fewer potential adopters.

The second feedback loop on the left is negative reinforcement (or "balancing" and hence labeled B). Clearly, growth cannot continue forever, because as more and more people adopt, there remain fewer and fewer potential adopters.

左边的第二个反馈回路是负强化(或“平衡” ，因此标记为 b)。显然，增长不可能永远持续下去，因为随着越来越多的人采用，潜在的采用者越来越少。

Both feedback loops act simultaneously, but at different times they may have different strengths. Thus one might expect growing sales in the initial years, and then declining sales in the later years. However, in general a causal loop diagram does not specify the structure of a system sufficiently to permit determination of its behavior from the visual representation alone.

Both feedback loops act simultaneously, but at different times they may have different strengths. Thus one might expect growing sales in the initial years, and then declining sales in the later years. However, in general a causal loop diagram does not specify the structure of a system sufficiently to permit determination of its behavior from the visual representation alone.

两种反馈循环同时发挥作用，但在不同的时间，它们可能有不同的优势。因此，人们可能会认为，最初几年的销售额会增长，随后几年销售额会下降。然而，一般来说，环路图并没有充分指定系统的结构，以允许仅仅通过视觉表现来确定其行为。

Stock and flow diagrams

库存和流程图

Causal loop diagrams aid in visualizing a system’s structure and behavior, and analyzing the system qualitatively. To perform a more detailed quantitative analysis, a causal loop diagram is transformed to a stock and flow diagram. A stock and flow model helps in studying and analyzing the system in a quantitative way; such models are usually built and simulated using computer software.

Causal loop diagrams aid in visualizing a system’s structure and behavior, and analyzing the system qualitatively. To perform a more detailed quantitative analysis, a causal loop diagram is transformed to a stock and flow diagram. A stock and flow model helps in studying and analyzing the system in a quantitative way; such models are usually built and simulated using computer software.

因果循环图有助于将系统的结构和行为可视化，并对系统进行定性分析。为了进行更详细的定量分析，环路图被转换成库存和流程图。库存和流量模型有助于对系统进行定量研究和分析，这些模型通常是用计算机软件建立和模拟的。

A stock is the term for any entity that accumulates or depletes over time. A flow is the rate of change in a stock.

A stock is the term for any entity that accumulates or depletes over time. A flow is the rate of change in a stock.

库存是指随着时间的推移而累积或消耗的任何实体。流量是股票的变化率。

A flow is the rate of accumulation of the stock

A flow is the rate of accumulation of the stock

流量是存量的积累速率

In our example, there are two stocks: Potential adopters and Adopters. There is one flow: New adopters. For every new adopter, the stock of potential adopters declines by one, and the stock of adopters increases by one.

In our example, there are two stocks: Potential adopters and Adopters. There is one flow: New adopters. For every new adopter, the stock of potential adopters declines by one, and the stock of adopters increases by one.

在我们的示例中，有两种股票: 潜在的采用者和采用者。只有一种流动: 新的采用者。对于每一个新的采用者，潜在采用者的数量减少了一个，而采用者的数量增加了一个。

Stock and flow diagram of New product adoption model

frame

框架

Equations

方程式

The real power of system dynamics is utilised through simulation. Although it is possible to perform the modeling in a spreadsheet, there are a variety of software packages that have been optimised for this.

The real power of system dynamics is utilised through simulation. Although it is possible to perform the modeling in a spreadsheet, there are a variety of software packages that have been optimised for this.

通过仿真实现了系统动力学的真正威力。尽管在电子表格中执行建模是可能的，但是已经为此优化了各种软件包。

The steps involved in a simulation are:

The steps involved in a simulation are:

模拟涉及的步骤如下:

• Define the problem boundary

• Identify the most important stocks and flows that change these stock levels

• Identify sources of information that impact the flows

• Identify the main feedback loops

• Draw a causal loop diagram that links the stocks, flows and sources of information

• Write the equations that determine the flows

• Estimate the parameters and initial conditions. These can be estimated using statistical methods, expert opinion, market research data or other relevant sources of information.

• Simulate the model and analyse results.

In this example, the equations that change the two stocks via the flow are:

In this example, the equations that change the two stocks via the flow are:

在这个例子中，通过流量改变两种股票的方程是:

[math]\displaystyle{  \ \mbox{Potential adopters} = \int_{0} ^{t} \mbox{-New adopters }\,dt  }[/math]

[math]\displaystyle{  \ \mbox{Potential adopters} = \int_{0} ^{t} \mbox{-New adopters }\,dt  }[/math]

数学{潜在采纳者} int {0}{ t } mbox {-New adopters } ，dt / math

<！ -- 我不想标记这个巨大的贡献，但是这难道不应该像 t (0)-sum (t (i))的潜在采用者那样吗？是的

[math]\displaystyle{  \ \mbox{Adopters} = \int_{0} ^{t} \mbox{New adopters }\,dt  }[/math]

[math]\displaystyle{  \ \mbox{Adopters} = \int_{0} ^{t} \mbox{New adopters }\,dt  }[/math]

数学{ Adopters } int {0}{ t } mbox { New Adopters } ，dt / math

Equations in discrete time

离散时间方程

List of all the equations in discrete time, in their order of execution in each year, for years 1 to 15 :

List of all the equations in discrete time, in their order of execution in each year, for years 1 to 15 :

离散时间内所有方程式的列表，按每年执行的次序，从第1年到第15年:

[math]\displaystyle{ 1) \ \mbox{Probability that contact has not yet adopted}=\mbox{Potential adopters} / (\mbox{Potential adopters } + \mbox{ Adopters})  }[/math]

[math]\displaystyle{ 1) \ \mbox{Probability that contact has not yet adopted}=\mbox{Potential adopters} / (\mbox{Potential adopters } + \mbox{ Adopters})  }[/math]

Math 1) mbox { contact 尚未采用} mbox { Potential Adopters } / ( mbox { Potential Adopters } + mbox { Adopters }) / math

[math]\displaystyle{ 2) \ \mbox{Imitators}=q \cdot \mbox{Adopters} \cdot \mbox{Probability that contact has not yet adopted} }[/math]

[math]\displaystyle{ 2) \ \mbox{Imitators}=q \cdot \mbox{Adopters} \cdot \mbox{Probability that contact has not yet adopted} }[/math]

数学2) mbox { Imitators } q cdot mbox { Adopters } cdot mbox {概率，该联系人尚未采用} / math

[math]\displaystyle{ 3) \ \mbox{Innovators}=p \cdot \mbox{Potential adopters}  }[/math]

[math]\displaystyle{ 3) \ \mbox{Innovators}=p \cdot \mbox{Potential adopters}  }[/math]

数学3) mbox { Innovators } p cdot mbox { Potential adopters } / math

[math]\displaystyle{ 4) \ \mbox{New adopters}=\mbox{Innovators}+\mbox{Imitators}  }[/math]

[math]\displaystyle{ 4) \ \mbox{New adopters}=\mbox{Innovators}+\mbox{Imitators}  }[/math]

数学4) mbox { New adopters } mbox { Innovators } + mbox { Imitators } / math

[math]\displaystyle{ 4.1) \ \mbox{Potential adopters}\ -= \mbox{New adopters } }[/math]

[math]\displaystyle{ 4.1) \ \mbox{Potential adopters}\ -= \mbox{New adopters } }[/math]

4.1) mbox { Potential adopters } - mbox { New adopters } / math

[math]\displaystyle{ 4.2) \ \mbox{Adopters}\ += \mbox{New adopters } }[/math]

[math]\displaystyle{ 4.2) \ \mbox{Adopters}\ += \mbox{New adopters } }[/math]

4.2) mbox { Adopters } mbox { New Adopters } / math

[math]\displaystyle{ \ p=0.03  }[/math]

[math]\displaystyle{ \ p=0.03  }[/math]

数学0.03 / 数学

[math]\displaystyle{ \ q=0.4  }[/math]

[math]\displaystyle{ \ q=0.4  }[/math]

数学0.4 / 数学

Dynamic simulation results

动态模拟结果

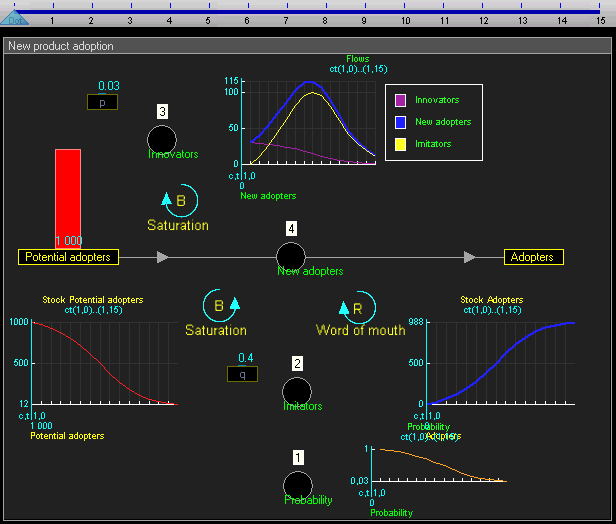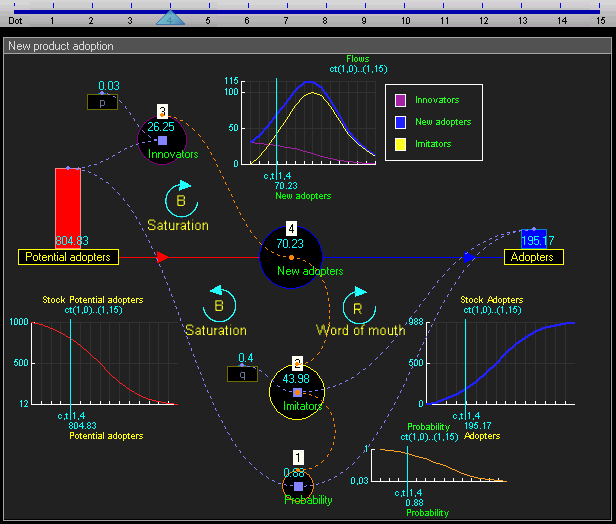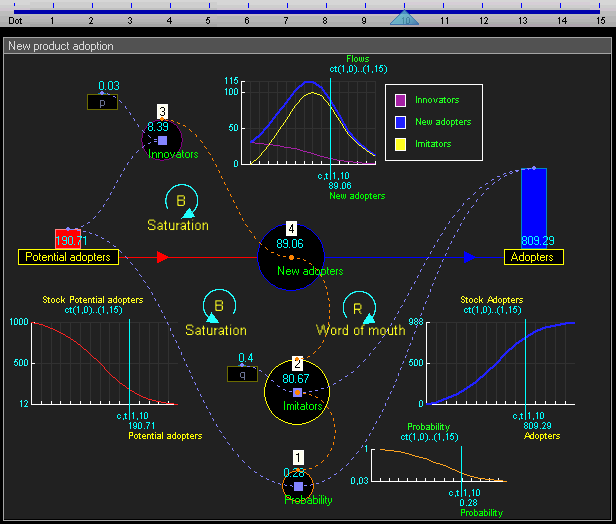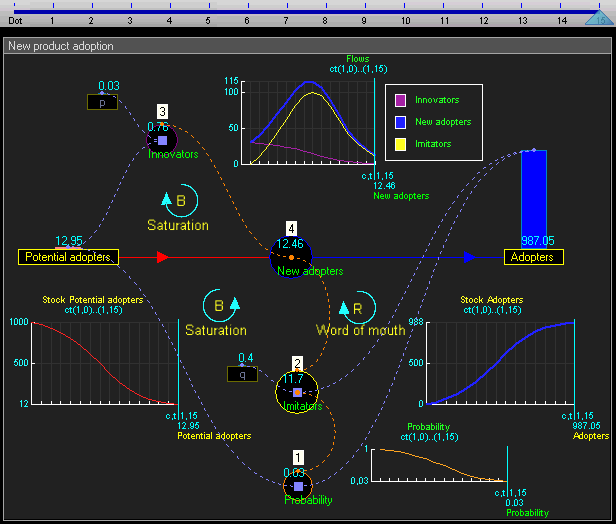
The dynamic simulation results show that the behaviour of the system would be to have growth in adopters that follows a classic s-curve shape.

The dynamic simulation results show that the behaviour of the system would be to have growth in adopters that follows a classic s-curve shape.

动态仿真结果表明，系统的行为将有增长的采纳者遵循一个经典的 s 曲线形状。 Br /

The increase in adopters is very slow initially, then exponential growth for a period, followed ultimately by saturation.

The increase in adopters is very slow initially, then exponential growth for a period, followed ultimately by saturation.

使用者的增长在一开始是非常缓慢的，然后是一段指数增长，最后是饱和。

Dynamic stock and flow diagram of New product adoption model

frame

框架

Stocks and flows values for years = 0 to 15

frame

框架

Equations in continuous time

连续时间方程

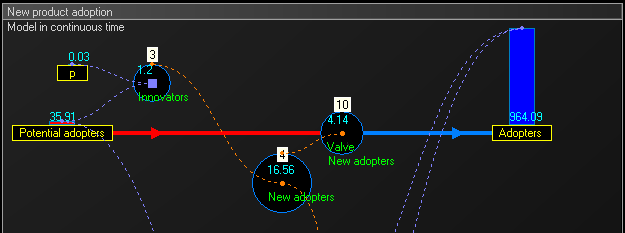
To get intermediate values and better accuracy, the model can run in continuous time: we multiply the number of units of time and we proportionally divide values that change stock levels. In this example we multiply the 15 years by 4 to obtain 60 trimesters, and we divide the value of the flow by 4.

To get intermediate values and better accuracy, the model can run in continuous time: we multiply the number of units of time and we proportionally divide values that change stock levels. In this example we multiply the 15 years by 4 to obtain 60 trimesters, and we divide the value of the flow by 4.

为了得到中间值和更好的准确性，该模型可以在连续时间内运行: 我们乘以时间单位的数量，并按比例除以改变库存水平的值。在这个例子中，我们把15年乘以4得到60个三个月，然后我们把流量的值除以4。 Br

Dividing the value is the simplest with the Euler method, but other methods could be employed instead, such as Runge–Kutta methods.

Dividing the value is the simplest with the Euler method, but other methods could be employed instead, such as Runge–Kutta methods.

用欧拉法除值是最简单的方法，但也可以用其他方法代替，如龙格-库塔法。

List of the equations in continuous time for trimesters = 1 to 60 :

List of the equations in continuous time for trimesters = 1 to 60 :

连续时间方程列表1至60的三个月:

• They are the same equations as in the section Equation in discrete time above, except equations 4.1 and 4.2 replaced by following :

[math]\displaystyle{ 10) \ \mbox{Valve New adopters}\ = \mbox{New adopters} \cdot TimeStep  }[/math]

[math]\displaystyle{ 10) \ \mbox{Valve New adopters}\ = \mbox{New adopters} \cdot TimeStep  }[/math]

10) mbox { Valve New adopters } mbox { New adopters } cdot TimeStep / math

[math]\displaystyle{ 10.1) \ \mbox{Potential adopters}\ -= \mbox{Valve New adopters}  }[/math]

[math]\displaystyle{ 10.1) \ \mbox{Potential adopters}\ -= \mbox{Valve New adopters}  }[/math]

数学10.1) mbox { Potential adopters } - mbox { Valve New adopters } / math

[math]\displaystyle{ 10.2) \ \mbox{Adopters}\ += \mbox{Valve New adopters }  }[/math]

[math]\displaystyle{ 10.2) \ \mbox{Adopters}\ += \mbox{Valve New adopters }  }[/math]

10.2) mbox { Adopters } mbox { Valve New Adopters } / math

[math]\displaystyle{  \ TimeStep = 1/4  }[/math]

[math]\displaystyle{  \ TimeStep = 1/4  }[/math]

数学 time step 1 / 4 / math

• In the below stock and flow diagram, the intermediate flow 'Valve New adopters' calculates the equation :

[math]\displaystyle{  \ \mbox{Valve New adopters}\ = \mbox{New adopters } \cdot TimeStep  }[/math]

[math]\displaystyle{  \ \mbox{Valve New adopters}\ = \mbox{New adopters } \cdot TimeStep  }[/math]

{ Valve New adopters } mbox { New adopters } cdot TimeStep / math

Dynamic stock and flow diagram of New product adoption model in continuous time

frame

框架

Application

申请

System dynamics has found application in a wide range of areas, for example population, agriculture, ecological and economic systems, which usually interact strongly with each other.

System dynamics has found application in a wide range of areas, for example population, agriculture, ecological and economic systems, which usually interact strongly with each other.

系统动力学在人口、农业、生态和经济系统等各个领域都有着广泛的应用，这些领域之间往往存在着强烈的相互作用。

System dynamics have various "back of the envelope" management applications. They are a potent tool to:

System dynamics have various "back of the envelope" management applications. They are a potent tool to:

系统动力学有各种各样的“封底”管理应用。它们是一个强有力的工具:

• Teach system thinking reflexes to persons being coached

• Analyze and compare assumptions and mental models about the way things work

• Gain qualitative insight into the workings of a system or the consequences of a decision

• Recognize archetypes of dysfunctional systems in everyday practice

Computer software is used to simulate a system dynamics model of the situation being studied. Running "what if" simulations to test certain policies on such a model can greatly aid in understanding how the system changes over time. System dynamics is very similar to systems thinking and constructs the same causal loop diagrams of systems with feedback. However, system dynamics typically goes further and utilises simulation to study the behaviour of systems and the impact of alternative policies.

Computer software is used to simulate a system dynamics model of the situation being studied. Running "what if" simulations to test certain policies on such a model can greatly aid in understanding how the system changes over time. System dynamics is very similar to systems thinking and constructs the same causal loop diagrams of systems with feedback. However, system dynamics typically goes further and utilises simulation to study the behaviour of systems and the impact of alternative policies.

用计算机软件对所研究的情况进行了系统动力学模型的仿真。在这样的模型上运行“如果”模拟来测试某些策略可以极大地帮助理解随着时间的推移系统如何变化。系统动力学与系统思维非常相似，构造了具有反馈的系统相同的因果循环图。然而，系统动力学通常走得更远，利用模拟来研究系统的行为和替代政策的影响。

System dynamics has been used to investigate resource dependencies, and resulting problems, in product development.

System dynamics has been used to investigate resource dependencies, and resulting problems, in product development.

系统动力学已经被用来研究产品开发中的资源依赖，以及由此产生的问题。

A system dynamics approach to macroeconomics, known as Minsky, has been developed by the economist Steve Keen. This has been used to successfully model world economic behaviour from the apparent stability of the Great Moderation to the sudden unexpected Financial crisis of 2007–08.

A system dynamics approach to macroeconomics, known as Minsky, has been developed by the economist Steve Keen. This has been used to successfully model world economic behaviour from the apparent stability of the Great Moderation to the sudden unexpected Financial crisis of 2007–08.

经济学家史蒂夫•基恩(Steve Keen)提出了一种宏观经济学的系统动力学方法——明斯基(Minsky)。从“大缓和”(Great Moderation)时期表面上的稳定，到2007年至2008年突如其来的金融危机，世界经济行为都成功地运用了这一模型。

Example

例子

Causal loop diagram of a model examining the growth or decline of a life insurance company.

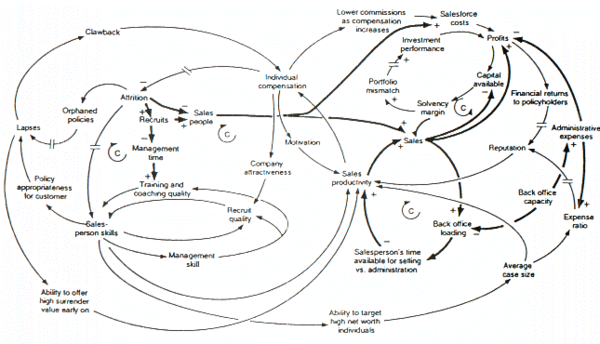
Causal loop diagram of a model examining the growth or decline of a life insurance company.

人寿保险公司的增长或衰退模型的环路图。

The figure above is a causal loop diagram of a system dynamics model created to examine forces that may be responsible for the growth or decline of life insurance companies in the United Kingdom. A number of this figure's features are worth mentioning. The first is that the model's negative feedback loops are identified by C's, which stand for Counteracting loops. The second is that double slashes are used to indicate places where there is a significant delay between causes (i.e., variables at the tails of arrows) and effects (i.e., variables at the heads of arrows). This is a common causal loop diagramming convention in system dynamics. Third, is that thicker lines are used to identify the feedback loops and links that author wishes the audience to focus on. This is also a common system dynamics diagramming convention. Last, it is clear that a decision maker would find it impossible to think through the dynamic behavior inherent in the model, from inspection of the figure alone.

The figure above is a causal loop diagram of a system dynamics model created to examine forces that may be responsible for the growth or decline of life insurance companies in the United Kingdom. A number of this figure's features are worth mentioning. The first is that the model's negative feedback loops are identified by C's, which stand for Counteracting loops. The second is that double slashes are used to indicate places where there is a significant delay between causes (i.e., variables at the tails of arrows) and effects (i.e., variables at the heads of arrows). This is a common causal loop diagramming convention in system dynamics. Third, is that thicker lines are used to identify the feedback loops and links that author wishes the audience to focus on. This is also a common system dynamics diagramming convention. Last, it is clear that a decision maker would find it impossible to think through the dynamic behavior inherent in the model, from inspection of the figure alone.

上面的数字是一个系统动力学模型的环路图，这个模型是为了研究可能对英国寿险公司的增长或衰退负有责任的力量而创建的。这个数字的一些特征值得一提。首先，模型的负反馈回路由 c 进行识别，c 代表抵消回路。第二种是双斜线用来表示原因(即箭头尾部的变量)和效果(即箭头头部的变量)之间存在显著延迟的地方。这是系统动力学中常见的因果循环图。第三，较粗的线条用来识别作者希望读者关注的反馈回路和链接。这也是一个常见的系统动力学图表惯例。最后，很明显，决策者不可能仅仅通过对数字的检查来思考模型中固有的动态行为。

Example of piston motion

活塞运动实例

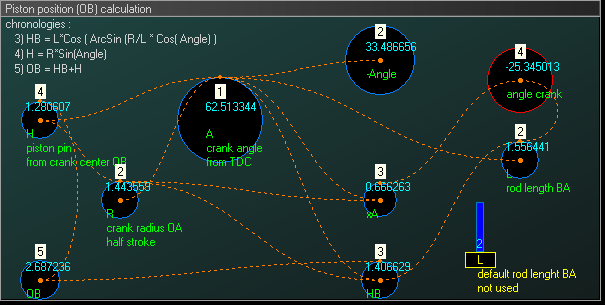
1. Objective: study of a crank-connecting rod system.
   We want to model a crank-connecting rod system through a system dynamic model. Two different full descriptions of the physical system with related systems of equations can be found here 模板:In lang and here 模板:In lang; they give the same results. In this example, the crank, with variable radius and angular frequency, will drive a piston with a variable connecting rod length.

Objective: study of a crank-connecting rod system.
 We want to model a crank-connecting rod system through a system dynamic model. Two different full descriptions of the physical system with related systems of equations can be found  here  and here ; they give the same results. In this example, the crank, with variable radius and angular frequency, will drive a piston with a variable connecting rod length.

目的: 研究曲柄连杆机构。 通过建立系统动力学模型，对曲柄连杆机构进行建模。在这里和这里可以找到对物理系统和相关方程组的两种不同的完整描述，它们给出了相同的结果。在这个例子中，可变半径和角频率的曲柄将驱动连杆长度可变的活塞。

1. System dynamic modeling: the system is now modeled, according to a stock and flow system dynamic logic.
   The figure below shows the stock and flow diagram
   

   Stock and flow diagram for crank-connecting rod system

System dynamic modeling: the system is now modeled, according to a stock and flow system dynamic logic.
 The figure below shows the stock and flow diagram frame

系统动态建模: 根据库存和流量系统的动态逻辑对系统进行建模。 Br / 下图显示了库存和流程图框架

1. Simulation: the behavior of the crank-connecting rod dynamic system can then be simulated.
   The next figure is a 3D simulation created using procedural animation. Variables of the model animate all parts of this animation: crank, radius, angular frequency, rod length, and piston position.

Simulation: the behavior of the crank-connecting rod dynamic system can then be simulated.
 The next figure is a 3D simulation created using procedural animation. Variables of the model animate all parts of this animation: crank, radius, angular frequency, rod length, and piston position.

仿真: 可以对曲柄连杆机构的动力学行为进行仿真。 Br / 下一个图形是使用过程动画创建的3D 模拟。模型的变量动画这个动画的所有部分: 曲柄，半径，角频率，连杆长度，和活塞的位置。

3D procedural animation of the crank-connecting rod system modeled in 2

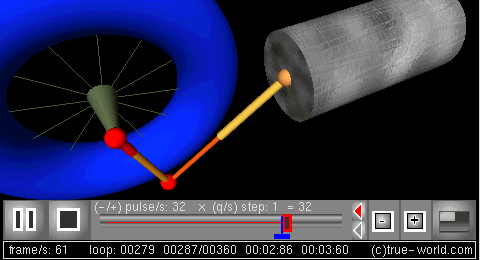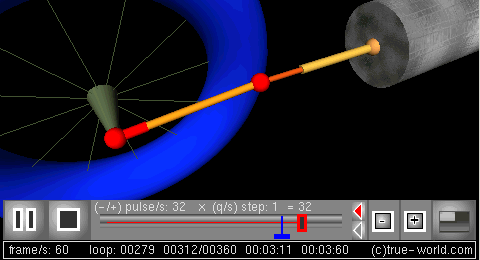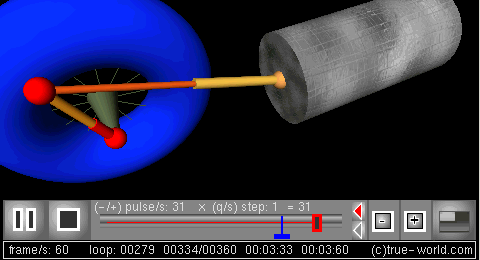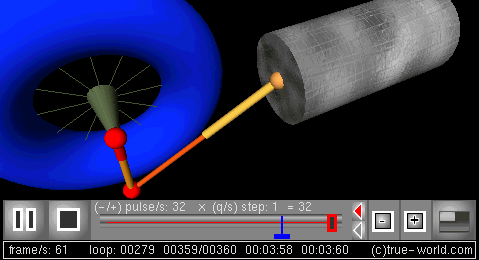
3D frame

三维动画[曲柄连杆机构的程序动画，2 | 帧]

See also

参见

Related subjects

Related subjects

相关科目

• Causal loop diagram

• Comparison of system dynamics software

• Ecosystem model

• Plateau Principle

• System archetypes

• System Dynamics Society

• Twelve leverage points

• Wicked problems

• World3

• Population dynamics

• Predator-prey interaction

Related fields

Related fields

相关领域

• Dynamical systems theory

• Grey box model

• Operations research

• Social dynamics

• System identification

• Systems theory

• Systems thinking

• TRIZ

Related scientists

Related scientists

相关科学家

• Jay Forrester

• Dennis Meadows

• Donella Meadows

• Peter Senge

• Graeme Snooks

• John Sterman

References

参考资料

Further reading

进一步阅读

• Kypuros, Javier (2013). System dynamics and control with bond graph modeling. Boca Raton: Taylor & Francis. ISBN 1466560754. 

• Forrester, Jay W. (1961). Industrial Dynamics. Pegasus Communications. ISBN 978-1-883823-36-8. 

• Forrester, Jay W. (1969). Urban Dynamics. Pegasus Communications. ISBN 978-1-883823-39-9. 

• Meadows, Donella H. (1972). Limits to Growth. New York: University books. ISBN 978-0-87663-165-2. 

• Morecroft, John (2007). Strategic Modelling and Business Dynamics: A Feedback Systems Approach. John Wiley & Sons. ISBN 978-0-470-01286-4. 

• Roberts, Edward B. (1978). Managerial Applications of System Dynamics. Cambridge: MIT Press. ISBN 978-0-262-18088-7. https://archive.org/details/managerialapplic0000unse. 

• Randers, Jorgen (1980). Elements of the System Dynamics Method. Cambridge: MIT Press. ISBN 978-0-915299-39-3. 

• Senge, Peter (1990). The Fifth Discipline. Currency. ISBN 978-0-385-26095-4. 

• Sterman, John D. (2000). Business Dynamics: Systems thinking and modeling for a complex world. McGraw Hill. ISBN 978-0-07-231135-8. 

External links

外部链接

• System Dynamics Society

• Study Prepared for the U.S. Department of Energy's Introducing System Dynamics -

• Desert Island Dynamics "An Annotated Survey of the Essential System Dynamics Literature"

Dynamics

动力学

Category:Operations research

类别: 运筹学

Category:Problem structuring methods

类别: 问题结构化方法

Category:Scientific modeling

类别: 科学建模

Dynamics

动力学

This page was moved from wikipedia:en:System dynamics. Its edit history can be viewed at 系统动力学/edithistory