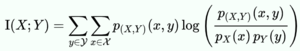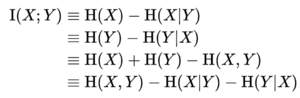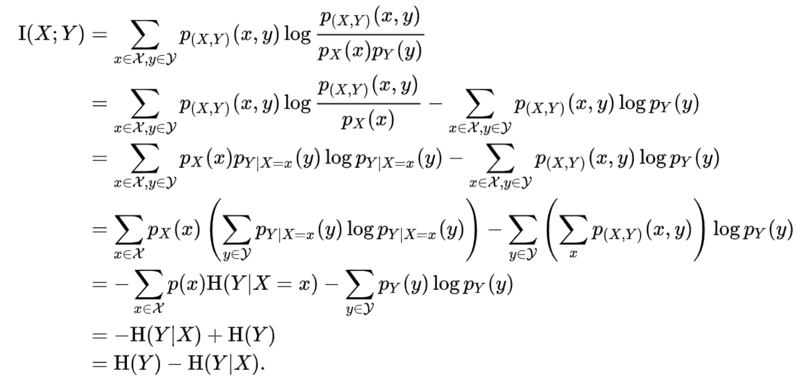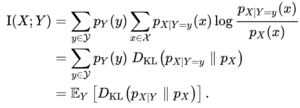“互信息”的版本间的差异
Yillia Jing(讨论 | 贡献) |
Yillia Jing(讨论 | 贡献) |
||
| 第704行: | 第704行: | ||
Normalized variants of the mutual information are provided by the coefficients of constraint, uncertainty coefficient or proficiency: | Normalized variants of the mutual information are provided by the coefficients of constraint, uncertainty coefficient or proficiency: | ||
| − | + | 互信息的规范化变量由约束系数、不确定系数或熟练程度组成: | |
:<math> | :<math> | ||
| 第710行: | 第710行: | ||
C_{XY} = \frac{\operatorname{I}(X;Y)}{H(Y)} | C_{XY} = \frac{\operatorname{I}(X;Y)}{H(Y)} | ||
| − | ~~~~\mbox{ | + | ~~~~\mbox{和}~~~~ |
C_{YX} = \frac{\operatorname{I}(X;Y)}{H(X)}. | C_{YX} = \frac{\operatorname{I}(X;Y)}{H(X)}. | ||
| 第722行: | 第722行: | ||
The two coefficients have a value ranging in [0, 1], but are not necessarily equal. In some cases a symmetric measure may be desired, such as the following redundancy measure: | The two coefficients have a value ranging in [0, 1], but are not necessarily equal. In some cases a symmetric measure may be desired, such as the following redundancy measure: | ||
| − | + | 这两个系数的值范围均为[0,1],但不一定是相等的。在某些情况下,可能需要一个对称的度量,例如下面的冗余度量: | |
:<math>R = \frac{\operatorname{I}(X;Y)}{H(X) + H(Y)}</math> | :<math>R = \frac{\operatorname{I}(X;Y)}{H(X) + H(Y)}</math> | ||
| 第733行: | 第733行: | ||
which attains a minimum of zero when the variables are independent and a maximum value of | which attains a minimum of zero when the variables are independent and a maximum value of | ||
| − | + | 当变量是独立的时候,它的最小值为零,最大值可以达到: | |
| 第755行: | 第755行: | ||
Another symmetrical measure is the symmetric uncertainty , given by | Another symmetrical measure is the symmetric uncertainty , given by | ||
| − | + | 另一个对称度量是对称不确定度,由下式表示: | |
| 第778行: | 第778行: | ||
If we consider mutual information as a special case of the total correlation or dual total correlation, the normalized version are respectively, | If we consider mutual information as a special case of the total correlation or dual total correlation, the normalized version are respectively, | ||
| − | + | 如果我们把互信息看作是'''<font color="#ff8000">总相关 Total correlation</font>'''或'''<font color="#ff8000">对偶总相关 Dual total correlation</font>'''的特殊情况,则其标准化版本分别为, | |
:<math>\frac{\operatorname{I}(X;Y)}{\min\left[ H(X),H(Y)\right]}</math> and <math>\frac{\operatorname{I}(X;Y)}{H(X,Y)} \; .</math> | :<math>\frac{\operatorname{I}(X;Y)}{\min\left[ H(X),H(Y)\right]}</math> and <math>\frac{\operatorname{I}(X;Y)}{H(X,Y)} \; .</math> | ||
| 第788行: | 第788行: | ||
This normalized version also known as Information Quality Ratio (IQR) which quantifies the amount of information of a variable based on another variable against total uncertainty: | This normalized version also known as Information Quality Ratio (IQR) which quantifies the amount of information of a variable based on another variable against total uncertainty: | ||
| − | + | 这个标准化版本也被称为'''<font color="#ff8000">信息质量比率 Information Quality Ratio,IQR</font>''' ,它根据另一个变量量化了一个变量的信息量,来对抗总的不确定性: | |
:<math>IQR(X, Y) = \operatorname{E}[\operatorname{I}(X;Y)] | :<math>IQR(X, Y) = \operatorname{E}[\operatorname{I}(X;Y)] | ||
| 第805行: | 第805行: | ||
There's a normalization which derives from first thinking of mutual information as an analogue to [[covariance]] (thus [[Entropy (information theory)|Shannon entropy]] is analogous to [[variance]]). Then the normalized mutual information is calculated akin to the [[Pearson product-moment correlation coefficient|Pearson correlation coefficient]], | There's a normalization which derives from first thinking of mutual information as an analogue to [[covariance]] (thus [[Entropy (information theory)|Shannon entropy]] is analogous to [[variance]]). Then the normalized mutual information is calculated akin to the [[Pearson product-moment correlation coefficient|Pearson correlation coefficient]], | ||
| − | + | 有一个标准化的名字——它起源于最初把互信息看作是'''<font color="#ff8000">协方差 Covariance</font>'''的类比(因此香农熵类似于方差)。然后计算归一化互信息类似于'''<font color="#ff8000">皮尔森相关系数 Pearson product-moment</font>''': | |
2020年8月19日 (三) 11:40的版本
此词条暂由彩云小译翻译,未经人工整理和审校,带来阅读不便,请见谅。模板:Information theory
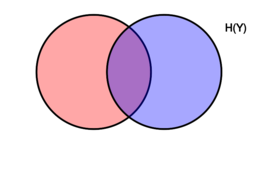
Venn diagram showing additive and subtractive relationships various information measures associated with correlated variables [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math]. The area contained by both circles is the joint entropy [math]\displaystyle{ H(X,Y) }[/math]. The circle on the left (red and violet) is the individual entropy [math]\displaystyle{ H(X) }[/math], with the red being the conditional entropy [math]\displaystyle{ H(X|Y) }[/math]. The circle on the right (blue and violet) is [math]\displaystyle{ H(Y) }[/math], with the blue being [math]\displaystyle{ H(Y|X) }[/math]. The violet is the mutual information [math]\displaystyle{ \operatorname{I}(X;Y) }[/math].
Venn diagram showing additive and subtractive relationships various information measures associated with correlated variables 𝑋 and 𝑌. The area contained by both circles is the joint entropy H(𝑋,𝑌). The circle on the left (red and violet) is the individual entropy H(𝑋), with the red being the conditional entropy H(𝑋|𝑌). The circle on the right (blue and violet) is H(𝑌), with the blue being H(𝑌|𝑋). The violet is the mutual information I(𝑋;𝑌).
这里的维恩图显示了各种信息间的交并补运算关系关系,这些信息都可以用来度量变量[math]\displaystyle{ X }[/math]和[math]\displaystyle{ Y }[/math]的各种相关性。图中所有面积(包括两个圆圈)表示二者的 联合熵 Joint entropy[math]\displaystyle{ H(X,Y) }[/math]。左侧的整个圆圈表示变量[math]\displaystyle{ X }[/math]的 独立熵 Individual entropy[math]\displaystyle{ H(X) }[/math],红色(差集)部分表示X的 条件熵 Conditional entropy[math]\displaystyle{ H(X|Y) }[/math]。右侧的整个圆圈表示变量[math]\displaystyle{ Y }[/math]的独立熵[math]\displaystyle{ H(Y) }[/math],蓝色(差集)部分表示X的条件熵[math]\displaystyle{ H(Y|X) }[/math]。两个圆中间的交集部分(紫色的部分)表示二者的互信息 Mutual information,MI[math]\displaystyle{ \operatorname{I}(X;Y) }[/math])。
In probability theory and information theory, the mutual information (MI) of two random variables is a measure of the mutual dependence between the two variables. More specifically, it quantifies the "amount of information" (in units such as shannons, commonly called bits) obtained about one random variable through observing the other random variable. The concept of mutual information is intricately linked to that of entropy of a random variable, a fundamental notion in information theory that quantifies the expected "amount of information" held in a random variable.
In probability theory and information theory, the mutual information (MI) of two random variables is a measure of the mutual dependence between the two variables. More specifically, it quantifies the "amount of information" (in units such as shannons, commonly called bits) obtained about one random variable through observing the other random variable. The concept of mutual information is intricately linked to that of entropy of a random variable, a fundamental notion in information theory that quantifies the expected "amount of information" held in a random variable.
在 概率论 Probability theory和 信息论 Information theory理论中,两个随机变量的 互信息 Mutual Information,MI是两个变量之间相互依赖程度的度量。更具体地说,它量化了通过观察一个随机变量而可以获得的关于另一个随机变量的“信息量”(单位如香农 Shannons,通常称为比特)。互信息的概念与随机变量的熵之间有着错综复杂的联系,熵是信息论中的一个基本概念,它量化了随机变量中所包含的预期“信息量”。
Not limited to real-valued random variables and linear dependence like the correlation coefficient, MI is more general and determines how different the joint distribution of the pair [math]\displaystyle{ (X,Y) }[/math] is to the product of the marginal distributions of [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math]. MI is the expected value of the pointwise mutual information (PMI).
Not limited to real-valued random variables and linear dependence like the correlation coefficient, MI is more general and determines how different the joint distribution of the pair [math]\displaystyle{ (X,Y) }[/math] is to the product of the marginal distributions of [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math]. MI is the expected value of the pointwise mutual information (PMI).
不仅限于实值随机变量和线性依赖之类的的相关系数,互信息表示的关系其实更加普遍,它决定了一对变量[math]\displaystyle{ (X,Y) }[/math]的联合分布与[math]\displaystyle{ X }[/math]和[math]\displaystyle{ Y }[/math]的边缘分布 Marginal distributions之积的不同程度。互信息是点互信息 Pointwise mutual information,PMI的期望值。
Mutual Information is also known as information gain.
Mutual Information is also known as information gain.
互信息也称为信息增益 Information gain。
定义 Definition
Let [math]\displaystyle{ (X,Y) }[/math] be a pair of random variables with values over the space [math]\displaystyle{ \mathcal{X}\times\mathcal{Y} }[/math]. If their joint distribution is [math]\displaystyle{ P_{(X,Y)} }[/math] and the marginal distributions are [math]\displaystyle{ P_X }[/math] and [math]\displaystyle{ P_Y }[/math], the mutual information is defined as
Let [math]\displaystyle{ (X,Y) }[/math] be a pair of random variables with values over the space [math]\displaystyle{ \mathcal{X}\times\mathcal{Y} }[/math]. If their joint distribution is [math]\displaystyle{ P_{(X,Y)} }[/math] and the marginal distributions are [math]\displaystyle{ P_X }[/math] and [math]\displaystyle{ P_Y }[/math], the mutual information is defined as
设一对随机变量[math]\displaystyle{ (X,Y) }[/math]的参数空间为[math]\displaystyle{ \mathcal{X}\times\mathcal{Y} }[/math]。若它们之间的的联合概率分布为[math]\displaystyle{ P_{(X,Y)} }[/math],边缘分布分别为[math]\displaystyle{ P_X }[/math]和[math]\displaystyle{ P_Y }[/math],则它们之间的互信息定义为:
where [math]\displaystyle{ D_{\mathrm{KL}} }[/math] is the Kullback–Leibler divergence.
其中[math]\displaystyle{ D_{\mathrm{KL}} }[/math]表示相对熵 Relative entropy,又称Kullback-Leibler散度。
Notice, as per property of the Kullback–Leibler divergence, that [math]\displaystyle{ I(X;Y) }[/math] is equal to zero precisely when the joint distribution coincides with the product of the marginals, i.e. when [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] are independent (and hence observing [math]\displaystyle{ Y }[/math] tells you nothing about [math]\displaystyle{ X }[/math]). In general [math]\displaystyle{ I(X;Y) }[/math] is non-negative, it is a measure of the price for encoding [math]\displaystyle{ (X,Y) }[/math] as a pair of independent random variables, when in reality they are not.
需要注意的是,根据Kullback–Leibler散度的性质,当两个随机变量的联合分布与其分别的边缘分布的乘积相等时,即当[math]\displaystyle{ X }[/math]和[math]\displaystyle{ Y }[/math]是相互独立的时,[math]\displaystyle{ I(X;Y) }[/math]等于零(因此已知[math]\displaystyle{ Y }[/math]的信息并不能得到任何关于[math]\displaystyle{ X }[/math]的信息)。一般来说,[math]\displaystyle{ I(X;Y) }[/math]是非负的,因为它是将[math]\displaystyle{ (X,Y) }[/math]作为一对独立随机变量来编码进而来进行价格(价值)度量的,但实际上它们并不一定是非负的。
关于离散分布的PMF In terms of PMFs for discrete distributions
The mutual information of two jointly discrete random variables [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] is calculated as a double sum:[1]:20
The mutual information of two jointly discrete random variables [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] is calculated as a double sum:
两个联合分布的离散型随机变量X和Y的互信息计算表现为双和的形式:
where [math]\displaystyle{ p_{(X,Y)} }[/math] is the joint probability mass function of [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math], and [math]\displaystyle{ p_X }[/math] and [math]\displaystyle{ p_Y }[/math] are the marginal probability mass functions of [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] respectively.
where [math]\displaystyle{ p_{(X,Y)} }[/math] is the joint probability mass function of [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math], and [math]\displaystyle{ p_X }[/math] and [math]\displaystyle{ p_Y }[/math] are the marginal probability mass functions of [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] respectively.
[math]\displaystyle{ p_{(X,Y)} }[/math]是[math]\displaystyle{ X }[/math]和[math]\displaystyle{ Y }[/math]的概率质量函数 Probability mass functions,而[math]\displaystyle{ p_X }[/math]和[math]\displaystyle{ p_Y }[/math]分别是数学[math]\displaystyle{ X }[/math]和[math]\displaystyle{ Y }[/math]的边缘概率质量函数 Marginal probability mass functions。
连续分布的PDF In terms of PDFs for continuous distributions
In the case of jointly continuous random variables, the double sum is replaced by a double integral:[1]:251
In the case of jointly continuous random variables, the double sum is replaced by a double integral:
在联合分布的随机变量为连续型的情况下,公式中的二重求和用二重积分代替:
where [math]\displaystyle{ p_{(X,Y)} }[/math] is now the joint probability density function of [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math], and [math]\displaystyle{ p_X }[/math] and [math]\displaystyle{ p_Y }[/math] are the marginal probability density functions of [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] respectively.
where [math]\displaystyle{ p_{(X,Y)} }[/math] is now the joint probability density function of [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math], and [math]\displaystyle{ p_X }[/math] and [math]\displaystyle{ p_Y }[/math] are the marginal probability density functions of [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] respectively.
式中,[math]\displaystyle{ p_{(X,Y)} }[/math]是[math]\displaystyle{ X }[/math]和[math]\displaystyle{ Y }[/math]的联合概率密度函数,而[math]\displaystyle{ p_X }[/math]和[math]\displaystyle{ p_Y }[/math]分别是[math]\displaystyle{ X }[/math]和[math]\displaystyle{ Y }[/math]的边缘概率密度函数 Probability density function。
If the log base 2 is used, the units of mutual information are bits.
If the log base 2 is used, the units of mutual information are bits.
如果以2为底取对数,则互信息的单位为位 bit。
动机 Motivation
Intuitively, mutual information measures the information that [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] share: It measures how much knowing one of these variables reduces uncertainty about the other. For example, if [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] are independent, then knowing [math]\displaystyle{ X }[/math] does not give any information about [math]\displaystyle{ Y }[/math] and vice versa, so their mutual information is zero. At the other extreme, if [math]\displaystyle{ X }[/math] is a deterministic function of [math]\displaystyle{ Y }[/math] and [math]\displaystyle{ Y }[/math] is a deterministic function of [math]\displaystyle{ X }[/math] then all information conveyed by [math]\displaystyle{ X }[/math] is shared with [math]\displaystyle{ Y }[/math]: knowing [math]\displaystyle{ X }[/math] determines the value of [math]\displaystyle{ Y }[/math] and vice versa. As a result, in this case the mutual information is the same as the uncertainty contained in [math]\displaystyle{ Y }[/math] (or [math]\displaystyle{ X }[/math]) alone, namely the entropy of [math]\displaystyle{ Y }[/math] (or [math]\displaystyle{ X }[/math]). Moreover, this mutual information is the same as the entropy of [math]\displaystyle{ X }[/math] and as the entropy of [math]\displaystyle{ Y }[/math]. (A very special case of this is when [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] are the same random variable.)
Intuitively, mutual information measures the information that [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] share: It measures how much knowing one of these variables reduces uncertainty about the other. For example, if [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] are independent, then knowing [math]\displaystyle{ X }[/math] does not give any information about [math]\displaystyle{ Y }[/math] and vice versa, so their mutual information is zero. At the other extreme, if [math]\displaystyle{ X }[/math] is a deterministic function of [math]\displaystyle{ Y }[/math] and [math]\displaystyle{ Y }[/math] is a deterministic function of [math]\displaystyle{ X }[/math] then all information conveyed by [math]\displaystyle{ X }[/math] is shared with [math]\displaystyle{ Y }[/math]: knowing [math]\displaystyle{ X }[/math] determines the value of [math]\displaystyle{ Y }[/math] and vice versa. As a result, in this case the mutual information is the same as the uncertainty contained in [math]\displaystyle{ Y }[/math] (or [math]\displaystyle{ X }[/math]) alone, namely the entropy of [math]\displaystyle{ Y }[/math] (or [math]\displaystyle{ X }[/math]). Moreover, this mutual information is the same as the entropy of [math]\displaystyle{ X }[/math] and as the entropy of [math]\displaystyle{ Y }[/math]. (A very special case of this is when [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] are the same random variable.)
直观地说,相互信息衡量了[math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math]的信息共享程度:它衡量了当已知其中一个变量后可以减少另一个变量多少的不确定性。例如,若[math]\displaystyle{ X }[/math]和[math]\displaystyle{ Y }[/math]是相互独立的,那么已知[math]\displaystyle{ X }[/math]不会得到关于[math]\displaystyle{ Y }[/math]的任何信息,反之亦然,因此它们之间的互信息为零。而另一种极端情况就是,若[math]\displaystyle{ X }[/math]是[math]\displaystyle{ Y }[/math]的确定函数,而[math]\displaystyle{ X }[/math]也是[math]\displaystyle{ X }[/math]自身的确定函数,则[math]\displaystyle{ X }[/math]传递的所有信息都与[math]\displaystyle{ Y }[/math]共享:即已知[math]\displaystyle{ X }[/math]就可以知道[math]\displaystyle{ Y }[/math]的值,反之亦然。因此,在这种情况下,互信息与仅包含在[math]\displaystyle{ Y }[/math](或[math]\displaystyle{ X }[/math])中的不确定性相同,即[math]\displaystyle{ Y }[/math](或[math]\displaystyle{ X }[/math])的熵相同。此外,这种情况下互信息与[math]\displaystyle{ X }[/math]的熵和[math]\displaystyle{ Y }[/math]的熵相同。(一个非常特殊的情况是当[math]\displaystyle{ X }[/math]和[math]\displaystyle{ Y }[/math]是相同的随机变量。)
Mutual information is a measure of the inherent dependence expressed in the joint distribution of [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] relative to the joint distribution of [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] under the assumption of independence. Mutual information therefore measures dependence in the following sense: [math]\displaystyle{ \operatorname{I}(X;Y)=0 }[/math] if and only if [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] are independent random variables. This is easy to see in one direction: if [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] are independent, then [math]\displaystyle{ p_{(X,Y)}(x,y)=p_X(x) \cdot p_Y(y) }[/math], and therefore:
Mutual information is a measure of the inherent dependence expressed in the joint distribution of 𝑋 and 𝑌 relative to the joint distribution of 𝑋 and 𝑌 under the assumption of independence. Mutual information therefore measures dependence in the following sense: I(𝑋;𝑌)=0 if and only if 𝑋 and 𝑌 are independent random variables. This is easy to see in one direction: if 𝑋 and 𝑌 are independent, then 𝑝(𝑋,𝑌)(𝑥,𝑦)=𝑝𝑋(𝑥)⋅𝑝𝑌(𝑦), and therefore:
互信息是在独立假设下,[math]\displaystyle{ X\lt /math和\lt math\gt Y }[/math]的联合分布相对于其内在相关性的度量。因此互信息是在以下条件下定义相关性的:[math]\displaystyle{ \operatorname{I}(X;Y)=0 }[/math]当且仅当[math]\displaystyle{ X\lt /math和\lt math\gt Y }[/math]是独立随机变量时。这很容易从一个方向看出:如果[math]\displaystyle{ X\lt /math和\lt math\gt Y }[/math]是独立的,那么[math]\displaystyle{ p_{(X,Y)}(x,y)=p_X(x) \cdot p_Y(y) }[/math],因此:
[math]\displaystyle{ \log{ \left( \frac{p_{(X,Y)}(x,y)}{p_X(x)\,p_Y(y)} \right) } = \log 1 = 0 . }[/math]
Moreover, mutual information is nonnegative (i.e. [math]\displaystyle{ \operatorname{I}(X;Y) \ge 0 }[/math] see below) and symmetric (i.e. [math]\displaystyle{ \operatorname{I}(X;Y) = \operatorname{I}(Y;X) }[/math] see below).
Moreover, mutual information is nonnegative (i.e. [math]\displaystyle{ \operatorname{I}(X;Y) \ge 0 }[/math] see below) and symmetric (i.e. [math]\displaystyle{ \operatorname{I}(X;Y) = \operatorname{I}(Y;X) }[/math] see below).
此外,互信息是非负的(例如:([math]\displaystyle{ \operatorname{I}(X;Y) \ge 0 }[/math],见下文)和对称的(即[math]\displaystyle{ \operatorname{I}(X;Y) = \operatorname{I}(Y;X) }[/math],见下文)。
与其他量的关系 Relation to other quantities
非负性 Nonnegativity
Using Jensen's inequality on the definition of mutual information we can show that [math]\displaystyle{ \operatorname{I}(X;Y) }[/math] is non-negative, i.e.[1]:28
Using Jensen's inequality on the definition of mutual information we can show that [math]\displaystyle{ \operatorname{I}(X;Y) }[/math] is non-negative, i.e.
利用琴生不等式 Jensen's inequality对互信息的定义进行推导,我们可以证明[math]\displaystyle{ \operatorname{I}(X;Y) }[/math]是非负的,即:
[math]\displaystyle{ \operatorname{I}(X;Y) \ge 0 }[/math]
对称性 Symmetry
[math]\displaystyle{ \operatorname{I}(X;Y) = \operatorname{I}(Y;X) }[/math]
条件熵与联合熵的关系 Relation to conditional and joint entropy
Mutual information can be equivalently expressed as:
Mutual information can be equivalently expressed as:
互信息也可以等价地表示为:
where [math]\displaystyle{ H(X) }[/math] and [math]\displaystyle{ H(Y) }[/math] are the marginal entropies, [math]\displaystyle{ H(X|Y) }[/math] and [math]\displaystyle{ H(Y|X) }[/math] are the conditional entropies, and [math]\displaystyle{ H(X,Y) }[/math] is the joint entropy of [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math].
其中[math]\displaystyle{ H(X) }[/math]和[math]\displaystyle{ H(Y) }[/math]是边际熵 Marginal entropy,[math]\displaystyle{ H(X|Y) }[/math]和[math]\displaystyle{ H(Y|X) }[/math]表示条件熵 Conditional entropy,[math]\displaystyle{ H(X,Y) }[/math]是[math]\displaystyle{ X }[/math]和[math]\displaystyle{ Y }[/math]的联合熵 Joint entropy。
Notice the analogy to the union, difference, and intersection of two sets: in this respect, all the formulas given above are apparent from the Venn diagram reported at the beginning of the article.
注意两个集合的并集、差集和交集的类比:在这方面,上面给出的所有公式都可以从文章开头的维恩图中看出。
In terms of a communication channel in which the output [math]\displaystyle{ Y }[/math] is a noisy version of the input [math]\displaystyle{ X }[/math], these relations are summarised in the figure:
就输出[math]\displaystyle{ Y }[/math]是输入[math]\displaystyle{ X }[/math]的噪声版本的通信信道而言,这些关系如图中总结所示:
Because [math]\displaystyle{ \operatorname{I}(X;Y) }[/math] is non-negative, consequently, [math]\displaystyle{ H(X) \ge H(X|Y) }[/math]. Here we give the detailed deduction of [math]\displaystyle{ \operatorname{I}(X;Y)=H(Y)-H(Y|X) }[/math] for the case of jointly discrete random variables:
因为[math]\displaystyle{ \operatorname{I}(X;Y) }[/math]是非负的,因此[math]\displaystyle{ H(X) \ge H(X|Y) }[/math]。这里我们给出了联合离散随机变量情形下结论[math]\displaystyle{ \operatorname{I}(X;Y)=H(Y)-H(Y|X) }[/math]的详细推导过程:
The proofs of the other identities above are similar. The proof of the general case (not just discrete) is similar, with integrals replacing sums.
同理,上述其他恒等式的证明方法都是是相似的。一般情况(不仅仅是离散情况)的证明是类似的,用积分代替求和。
Intuitively, if entropy [math]\displaystyle{ H(Y) }[/math] is regarded as a measure of uncertainty about a random variable, then [math]\displaystyle{ H(Y|X) }[/math] is a measure of what [math]\displaystyle{ X }[/math] does not say about [math]\displaystyle{ Y }[/math]. This is "the amount of uncertainty remaining about [math]\displaystyle{ Y }[/math] after [math]\displaystyle{ X }[/math] is known", and thus the right side of the second of these equalities can be read as "the amount of uncertainty in [math]\displaystyle{ Y }[/math], minus the amount of uncertainty in [math]\displaystyle{ Y }[/math] which remains after [math]\displaystyle{ X }[/math] is known", which is equivalent to "the amount of uncertainty in [math]\displaystyle{ Y }[/math] which is removed by knowing [math]\displaystyle{ X }[/math]". This corroborates the intuitive meaning of mutual information as the amount of information (that is, reduction in uncertainty) that knowing either variable provides about the other.
Intuitively, if entropy 𝐻(𝑌) is regarded as a measure of uncertainty about a random variable, then 𝐻(𝑌|𝑋) is a measure of what 𝑋 does not say about 𝑌. This is "the amount of uncertainty remaining about 𝑌 after 𝑋 is known", and thus the right side of the second of these equalities can be read as "the amount of uncertainty in 𝑌, minus the amount of uncertainty in 𝑌 which remains after 𝑋 is known", which is equivalent to "the amount of uncertainty in 𝑌 which is removed by knowing 𝑋". This corroborates the intuitive meaning of mutual information as the amount of information (that is, reduction in uncertainty) that knowing either variable provides about the other.
理论上来说,如果熵[math]\displaystyle{ H(Y) }[/math]被视为随机变量不确定性的度量,那么[math]\displaystyle{ H(Y|X) }[/math]则是对[math]\displaystyle{ X }[/math]没有说明[math]\displaystyle{ Y }[/math]的程度的度量。也就是“已知[math]\displaystyle{ X }[/math]后,关于[math]\displaystyle{ Y }[/math]剩余的不确定性”的度量,因此这些等式中第二个等式的右侧可以解读为“[math]\displaystyle{ Y }[/math]中的不确定性量,减去已知[math]\displaystyle{ X }[/math]后仍然存在的不确定性的量”,相当于“已知后消除的[math]\displaystyle{ Y }[/math]中的不确定性量”[math]\displaystyle{ X }[/math]".这证实了相互信息的直观含义就是了解其中一个变量提供的关于另一个变量的信息量(即不确定性的减少程度)。
Note that in the discrete case [math]\displaystyle{ H(X|X) = 0 }[/math] and therefore [math]\displaystyle{ H(X) = \operatorname{I}(X;X) }[/math]. Thus [math]\displaystyle{ \operatorname{I}(X; X) \ge \operatorname{I}(X; Y) }[/math], and one can formulate the basic principle that a variable contains at least as much information about itself as any other variable can provide.
注意,在离散情况下,[math]\displaystyle{ H(X|X) = 0 }[/math],因此[math]\displaystyle{ H(X) = \operatorname{I}(X;X) }[/math]。所以,[math]\displaystyle{ \operatorname{I}(X; X) \ge \operatorname{I}(X; Y) }[/math],据此我们可以得到一个基本结论,那就是一个变量至少包含与任何其他变量所能提供的关于自身的信息量的这么多信息。
与相对熵的关系 Relation to Kullback–Leibler divergence
For jointly discrete or jointly continuous pairs [math]\displaystyle{ (X,Y) }[/math],
For jointly discrete or jointly continuous pairs [math]\displaystyle{ (X,Y) }[/math],
对于联合的离散或连续分布变量对[math]\displaystyle{ (X,Y) }[/math],
mutual information is the Kullback–Leibler divergence of the product of the marginal distributions, [math]\displaystyle{ p_X \cdot p_Y }[/math], from the joint distribution [math]\displaystyle{ p_{(X,Y)} }[/math], that is,
mutual information is the Kullback–Leibler divergence of the product of the marginal distributions, 𝑝𝑋⋅𝑝𝑌, from the joint distribution 𝑝(𝑋,𝑌), that is,
互信息是边缘分布乘积的相对熵 [math]\displaystyle{ D_{KL} }[/math],也就是联合分布[math]\displaystyle{ p_{(X,Y)} }[/math]的乘积,即:
Furthermore, let [math]\displaystyle{ p_{X|Y=y}(x) = p_{(X,Y)}(x,y) / p_Y(y) }[/math] be the conditional mass or density function. Then, we have the identity
Furthermore, let [math]\displaystyle{ p_{X|Y=y}(x) = p_{(X,Y)}(x,y) / p_Y(y) }[/math] be the conditional mass or density function. Then, we have the identity
进一步地,设[math]\displaystyle{ p_{X|Y=y}(x) = p_{(X,Y)}(x,y) / p_Y(y) }[/math]为条件质量或密度函数。那么,我们就可以给出:
The proof for jointly discrete random variables is as follows:
The proof for jointly discrete random variables is as follows:
联合离散随机变量的证明如下:
Similarly this identity can be established for jointly continuous random variables.
Similarly this identity can be established for jointly continuous random variables.
这个恒等式在联合、连续的随机变量情况下同样成立。
Note that here the Kullback–Leibler divergence involves integration over the values of the random variable [math]\displaystyle{ X }[/math] only, and the expression [math]\displaystyle{ D_\text{KL}(p_{X|Y} \parallel p_X) }[/math] still denotes a random variable because [math]\displaystyle{ Y }[/math] is random. Thus mutual information can also be understood as the expectation of the Kullback–Leibler divergence of the univariate distribution [math]\displaystyle{ p_X }[/math] of [math]\displaystyle{ X }[/math] from the conditional distribution [math]\displaystyle{ p_{X|Y} }[/math] of [math]\displaystyle{ X }[/math] given [math]\displaystyle{ Y }[/math]: the more different the distributions [math]\displaystyle{ p_{X|Y} }[/math] and [math]\displaystyle{ p_X }[/math] are on average, the greater the information gain.
Note that here the Kullback–Leibler divergence involves integration over the values of the random variable [math]\displaystyle{ X }[/math] only, and the expression [math]\displaystyle{ D_\text{KL}(p_{X|Y} \parallel p_X) }[/math] still denotes a random variable because [math]\displaystyle{ Y }[/math] is random. Thus mutual information can also be understood as the expectation of the Kullback–Leibler divergence of the univariate distribution [math]\displaystyle{ p_X }[/math] of [math]\displaystyle{ X }[/math] from the conditional distribution [math]\displaystyle{ p_{X|Y} }[/math] of [math]\displaystyle{ X }[/math] given [math]\displaystyle{ Y }[/math]: the more different the distributions [math]\displaystyle{ p_{X|Y} }[/math] and [math]\displaystyle{ p_X }[/math] are on average, the greater the information gain.
因此,互信息也可以理解为X的单变量分布[math]\displaystyle{ p_X }[/math]与给定[math]\displaystyle{ Y }[/math]的[math]\displaystyle{ X }[/math]的条件分布[math]\displaystyle{ p_{X|Y} }[/math]的相对熵的期望:平均分布[math]\displaystyle{ p_{X|Y} }[/math]和[math]\displaystyle{ p_X }[/math]的分布差异越大,信息增益越大。
互信息的贝叶斯估计 Bayesian estimation of mutual information
It is well-understood how to do Bayesian estimation of the mutual information of a joint distribution based on samples of that distribution.
It is well-understood how to do Bayesian estimation of the mutual information of a joint distribution based on samples of that distribution.
如何根据联合分布的样本对联合分布的互信息进行贝叶斯估计,是一个众所周知的问题
The first work to do this, which also showed how to do Bayesian estimation of many other information-theoretic properties besides mutual information, was [2]. Subsequent researchers have rederived [3] and extended [4]this analysis.
关于这方面的第一项工作是文献[2]。后来的研究人员重新推导了文献[3]中的内容,并扩展了关于[4]的分析。
See [5]for a recent paper based on a prior specifically tailored to estimation of mutual information per se.
最近的一篇论文[5],该论文基于一个专门针对相互信息本身估计的先验知识。
Besides, recently an estimation method accounting for continuous and multivariate outputs, [math]\displaystyle{ Y }[/math], was proposed in [6].
此外,最近文献[6]提出了一种考虑连续多种输出变量𝑌的估计方法。
独立性假设 Independence assumptions
The Kullback-Leibler divergence formulation of the mutual information is predicated on that one is interested in comparing [math]\displaystyle{ p(x,y) }[/math] to the fully factorized outer product [math]\displaystyle{ p(x) \cdot p(y) }[/math]. In many problems, such as non-negative matrix factorization, one is interested in less extreme factorizations; specifically, one wishes to compare [math]\displaystyle{ p(x,y) }[/math] to a low-rank matrix approximation in some unknown variable [math]\displaystyle{ w }[/math]; that is, to what degree one might have
The Kullback-Leibler divergence formulation of the mutual information is predicated on that one is interested in comparing 𝑝(𝑥,𝑦) to the fully factorized outer product 𝑝(𝑥)⋅𝑝(𝑦). In many problems, such as non-negative matrix factorization, one is interested in less extreme factorizations; specifically, one wishes to compare 𝑝(𝑥,𝑦) to a low-rank matrix approximation in some unknown variable 𝑤; that is, to what degree one might have
相互信息的Kullback-Leibler散度公式是基于这样一个结论的:人们会更关注将[math]\displaystyle{ p(x,y) }[/math]与完全分解的外积[math]\displaystyle{ p(x) \cdot p(y) }[/math]进行比较。在许多问题中,例如非负矩阵因式分解中,人们对较不极端的因式分解感兴趣;具体地说,人们希望将[math]\displaystyle{ p(x,y) }[/math]与某个未知变量[math]\displaystyle{ w }[/math]中的低秩矩阵近似进行比较;也就是说,在多大程度上可能会有这样的结果:
- [math]\displaystyle{ p(x,y)\approx \sum_w p^\prime (x,w) p^{\prime\prime}(w,y) }[/math]
Alternately, one might be interested in knowing how much more information [math]\displaystyle{ p(x,y) }[/math] carries over its factorization. In such a case, the excess information that the full distribution [math]\displaystyle{ p(x,y) }[/math] carries over the matrix factorization is given by the Kullback-Leibler divergence
Alternately, one might be interested in knowing how much more information 𝑝(𝑥,𝑦) carries over its factorization. In such a case, the excess information that the full distribution 𝑝(𝑥,𝑦) carries over the matrix factorization is given by the Kullback-Leibler divergence
另一方面,人们可能有兴趣知道在因子分解过程中,有[math]\displaystyle{ p(x,y) }[/math]携带了多少信息。在这种情况下,全分布[math]\displaystyle{ p(x,y) }[/math]通过矩阵因子分解所携带的多余信息由Kullback-Leibler散度给出
- [math]\displaystyle{ \operatorname{I}_{LRMA} = \sum_{y \in \mathcal{Y}} \sum_{x \in \mathcal{X}} {p(x,y) \log{ \left(\frac{p(x,y)}{\sum_w p^\prime (x,w) p^{\prime\prime}(w,y)} \right) }}, }[/math]
The conventional definition of the mutual information is recovered in the extreme case that the process [math]\displaystyle{ W }[/math] has only one value for [math]\displaystyle{ w }[/math].
The conventional definition of the mutual information is recovered in the extreme case that the process [math]\displaystyle{ W }[/math] has only one value for [math]\displaystyle{ w }[/math].
在过程[math]\displaystyle{ w }[/math]只有一个值的极端情况下,可以使用传统的互信息定义。
变形 Variations
Several variations on mutual information have been proposed to suit various needs. Among these are normalized variants and generalizations to more than two variables.
Several variations on mutual information have been proposed to suit various needs. Among these are normalized variants and generalizations to more than two variables.
为了适应不同的需要,已经提出了几种互信息的变形。其中包括对两个以上变量的规范化变量和泛化。
度量 Metric
Many applications require a metric, that is, a distance measure between pairs of points. The quantity
Many applications require a metric, that is, a distance measure between pairs of points. The quantity
许多应用需要一个度量,即点对之间的距离度量。这个量:
- [math]\displaystyle{ \begin{align} d(X,Y) &= H(X,Y) - \operatorname{I}(X;Y) \\ &= H(X) + H(Y) - 2\operatorname{I}(X;Y) \\ &= H(X|Y) + H(Y|X) \end{align} }[/math]
satisfies the properties of a metric (triangle inequality, non-negativity, indiscernability and symmetry). This distance metric is also known as the variation of information.
satisfies the properties of a metric (triangle inequality, non-negativity, indiscernability and symmetry). This distance metric is also known as the variation of information.
满足度量的性质(三角形不等式、非负性、不可除性和对称性)。这种距离度量也称为信息的变化。
If [math]\displaystyle{ X, Y }[/math] are discrete random variables then all the entropy terms are non-negative, so [math]\displaystyle{ 0 \le d(X,Y) \le H(X,Y) }[/math] and one can define a normalized distance
If 𝑋,𝑌 are discrete random variables then all the entropy terms are non-negative, so 0≤𝑑(𝑋,𝑌)≤𝐻(𝑋,𝑌) and one can define a normalized distance
如果[math]\displaystyle{ X, Y }[/math]是离散随机变量,那么所有熵项都是非负的,因此[math]\displaystyle{ 0 \le d(X,Y) \le H(X,Y) }[/math],可以定义一个标准化距离:
- [math]\displaystyle{ D(X,Y) = \frac{d(X, Y)}{H(X, Y)} \le 1. }[/math]
The metric [math]\displaystyle{ D }[/math] is a universal metric, in that if any other distance measure places [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] close-by, then the [math]\displaystyle{ D }[/math] will also judge them close.[7]模板:Dubious
The metric 𝐷 is a universal metric, in that if any other distance measure places 𝑋 and 𝑌 close-by, then the 𝐷 will also judge them close.
度量[math]\displaystyle{ D }[/math]是一种通用度量,即如果任何其他距离度量将[math]\displaystyle{ X }[/math]和[math]\displaystyle{ Y }[/math]认为是近的,则[math]\displaystyle{ D }[/math]也将判断它们接近。
Plugging in the definitions shows that
Plugging in the definitions shows that
从如下定义可以看出:
- [math]\displaystyle{ D(X,Y) = 1 - \frac{\operatorname{I}(X; Y)}{H(X, Y)}. }[/math]
In a set-theoretic interpretation of information (see the figure for Conditional entropy), this is effectively the Jaccard distance between [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math].
In a set-theoretic interpretation of information (see the figure for Conditional entropy), this is effectively the Jaccard distance between 𝑋 and 𝑌.
在信息的集合论解释中(参见条件熵的图),这实际上就是[math]\displaystyle{ X }[/math]和[math]\displaystyle{ Y }[/math]之间的杰卡德距离 Jaccard distance。
Finally,
Finally,
最后,
- [math]\displaystyle{ D^\prime(X, Y) = 1 - \frac{\operatorname{I}(X; Y)}{\max\left\{H(X), H(Y)\right\}} }[/math]
is also a metric.
is also a metric.
也是一种度量标准。
条件互信息 Conditional mutual information
Sometimes it is useful to express the mutual information of two random variables conditioned on a third.
Sometimes it is useful to express the mutual information of two random variables conditioned on a third.
有时度量两个随机变量在以第三个随机变量为条件的情况下的相互信息也是有意义的。
[math]\displaystyle{ \operatorname{I}(X;Y|Z) = \mathbb{E}_Z [D_{\mathrm{KL}}( P_{(X,Y)|Z} \| P_{X|Z} \otimes P_{Y|Z} )] }[/math]
For jointly discrete random variables this takes the form
For jointly discrete random variables this takes the form
对于联合离散随机变量,这采用以下形式:
- [math]\displaystyle{ \operatorname{I}(X;Y|Z) = \sum_{z\in \mathcal{Z}} \sum_{y\in \mathcal{Y}} \sum_{x\in \mathcal{X}} {p_Z(z)\, p_{X,Y|Z}(x,y|z) \log\left[\frac{p_{X,Y|Z}(x,y|z)}{p_{X|Z}\,(x|z)p_{Y|Z}(y|z)}\right]}, }[/math]
which can be simplified as
which can be simplified as
可以简化为
- [math]\displaystyle{ \operatorname{I}(X;Y|Z) = \sum_{z\in \mathcal{Z}} \sum_{y\in \mathcal{Y}} \sum_{x\in \mathcal{X}} p_{X,Y,Z}(x,y,z) \log \frac{p_{X,Y,Z}(x,y,z)p_{Z}(z)}{p_{X,Z}(x,z)p_{Y,Z}(y,z)}. }[/math]
For jointly continuous random variables this takes the form
For jointly continuous random variables this takes the form
对于联合连续的随机变量,其形式为:
- [math]\displaystyle{ \operatorname{I}(X;Y|Z) = \int_{\mathcal{Z}} \int_{\mathcal{Y}} \int_{\mathcal{X}} {p_Z(z)\, p_{X,Y|Z}(x,y|z) \log\left[\frac{p_{X,Y|Z}(x,y|z)}{p_{X|Z}\,(x|z)p_{Y|Z}(y|z)}\right]} dx dy dz, }[/math]
which can be simplified as
which can be simplified as
可以简化为
- [math]\displaystyle{ \operatorname{I}(X;Y|Z) = \int_{\mathcal{Z}} \int_{\mathcal{Y}} \int_{\mathcal{X}} p_{X,Y,Z}(x,y,z) \log \frac{p_{X,Y,Z}(x,y,z)p_{Z}(z)}{p_{X,Z}(x,z)p_{Y,Z}(y,z)} dx dy dz. }[/math]
Conditioning on a third random variable may either increase or decrease the mutual information, but it is always true that
Conditioning on a third random variable may either increase or decrease the mutual information, but it is always true that
第三个随机变量的条件作用可能增加或减少互信息,但下式始终是成立的:
- [math]\displaystyle{ \operatorname{I}(X;Y|Z) \ge 0 }[/math]
for discrete, jointly distributed random variables [math]\displaystyle{ X,Y,Z }[/math]. This result has been used as a basic building block for proving other inequalities in information theory.
for discrete, jointly distributed random variables [math]\displaystyle{ X,Y,Z }[/math]. This result has been used as a basic building block for proving other inequalities in information theory.
对于离散的、联合分布的随机变量[math]\displaystyle{ X,Y,Z }[/math]。这一结果被用作证明信息论中其他不等式的基本组成部分。
多元互信息 Multivariate mutual information
Several generalizations of mutual information to more than two random variables have been proposed, such as total correlation (or multi-information) and interaction information. The expression and study of multivariate higher-degree mutual-information was achieved in two seemingly independent works: McGill (1954) [8] who called these functions “interaction information”, and Hu Kuo Ting (1962) [9] who also first proved the possible negativity of mutual-information for degrees higher than 2 and justified algebraically the intuitive correspondence to Venn diagrams [10]
Several generalizations of mutual information to more than two random variables have been proposed, such as total correlation (or multi-information) and interaction information. The expression and study of multivariate higher-degree mutual-information was achieved in two seemingly independent works: McGill (1954) who called these functions “interaction information”, and Hu Kuo Ting (1962) who also first proved the possible negativity of mutual-information for degrees higher than 2 and justified algebraically the intuitive correspondence to Venn diagrams
目前提出了许多将互信息推广到两个以上随机变量的方法,如全相关 Total correlation(或多信息 Multi-information)以及交互信息 Interaction information。多元高阶互信息的表达和研究是在两部看似独立的著作中实现的:McGill(1954年)在文献[8]中将这些函数统称为“互信息”,胡国亭(1962年)也在文献[9]中首次证明了大于2度的互信息可能是负的,并在文献[10]中用代数的方法证明了互信息和维恩图的直观对应关系。
- [math]\displaystyle{ \operatorname{I}(X_1;X_1) = H(X_1) }[/math]
and for [math]\displaystyle{ n \gt 1, }[/math]
and for 𝑛>1,
而对于𝑛>1,有:
- [math]\displaystyle{ \operatorname{I}(X_1;\,...\,;X_n) = \operatorname{I}(X_1;\,...\,;X_{n-1}) - \operatorname{I}(X_1;\,...\,;X_{n-1}|X_n), }[/math]
where (as above) we define
where (as above) we define
综上所述,我们定义:
- [math]\displaystyle{ I(X_1;\ldots;X_{n-1}|X_{n}) = \mathbb{E}_{X_{n}} [D_{\mathrm{KL}}( P_{(X_1,\ldots,X_{n-1})|X_{n}} \| P_{X_1|X_{n}} \otimes\cdots\otimes P_{X_{n-1}|X_{n}} )]. }[/math]
(This definition of multivariate mutual information is identical to that of interaction information except for a change in sign when the number of random variables is odd.)
(This definition of multivariate mutual information is identical to that of interaction information except for a change in sign when the number of random variables is odd.)
(这个多元互信息的定义与互信息的定义相同,对于随机变量的数目为奇数时符号的变化除外。)
多元统计独立性 Multivariate statistical independence
The multivariate mutual-information functions generalize the pairwise independence case that states that [math]\displaystyle{ X_1,X_2 }[/math] if and only if [math]\displaystyle{ I(X_1;X_2)=0 }[/math], to arbitrary numerous variable. n variables are mutually independent if and only if the [math]\displaystyle{ 2^n-n-1 }[/math] mutual information functions vanish [math]\displaystyle{ I(X_1;...;X_k)=0 }[/math] with [math]\displaystyle{ n \ge k \ge 2 }[/math] (theorem 2 [10]). In this sense, the [math]\displaystyle{ I(X_1;...;X_k)=0 }[/math] can be used as a refined statistical independence criterion.
The multivariate mutual-information functions generalize the pairwise independence case that states that 𝑋1,𝑋2 if and only if 𝐼(𝑋1;𝑋2)=0, to arbitrary numerous variable. n variables are mutually independent if and only if the 2𝑛−𝑛−1 mutual information functions vanish 𝐼(𝑋1;...;𝑋𝑘)=0 with 𝑛≥𝑘≥2 (theorem 2). In this sense, the 𝐼(𝑋1;...;𝑋𝑘)=0 can be used as a refined statistical independence criterion.
多元互信息函数将[math]\displaystyle{ I(X_1;X_2)=0 }[/math]当且仅当[math]\displaystyle{ X_1,X_2 }[/math]两两独立的情况推广到任意多变量。即当且仅当[math]\displaystyle{ 2^n-n-1 }[/math]的互信息函数为[math]\displaystyle{ I(X_1;...;X_k)=0 }[/math]且math>n \ge k \ge 2</math>时,n个变量相互独立(定理2)。从这个意义上讲,[math]\displaystyle{ I(X_1;...;X_k)=0 }[/math]可以用作一个精确的统计独立性标准。
应用 Applications
For 3 variables, Brenner et al. applied multivariate mutual information to neural coding and called its negativity "synergy" [11] and Watkinson et al. applied it to genetic expression [12]. For arbitrary k variables, Tapia et al. applied multivariate mutual information to gene expression [13] [10]). It can be zero, positive, or negative [14]. The positivity corresponds to relations generalizing the pairwise correlations, nullity corresponds to a refined notion of independence, and negativity detects high dimensional "emergent" relations and clusterized datapoints [13]).
For 3 variables, Brenner et al. applied multivariate mutual information to neural coding and called its negativity "synergy" and Watkinson et al. applied it to genetic expression . For arbitrary k variables, Tapia et al. applied multivariate mutual information to gene expression . The positivity corresponds to relations generalizing the pairwise correlations, nullity corresponds to a refined notion of independence, and negativity detects high dimensional "emergent" relations and clusterized datapoints .
对于3个变量,Brenner等人将多变量互信息应用到神经编码中,并将其称为负面“协同作用” Negativity "synergy",接着Watkinson 等人将其应用到基因表达上。对于任意k个变量,Tapia 等人将多元互信息应用于基因表达——正性对应于一般化成对相关性的关系,无效性对应于一个精确的独立性概念,负性检测高维“涌现”关系和聚合数据点。
One high-dimensional generalization scheme which maximizes the mutual information between the joint distribution and other target variables is found to be useful in feature selection.[15]
One high-dimensional generalization scheme which maximizes the mutual information between the joint distribution and other target variables is found to be useful in feature selection.
目前已经提出了一种能够最大化联合分布与其他目标变量之间的互信息的高维推广方案,该方法可用于 特征选择 Feature selection。
Mutual information is also used in the area of signal processing as a measure of similarity between two signals. For example, FMI metric[16] is an image fusion performance measure that makes use of mutual information in order to measure the amount of information that the fused image contains about the source images. The Matlab code for this metric can be found at.[17]
Mutual information is also used in the area of signal processing as a measure of similarity between two signals. For example, FMI metric is an image fusion performance measure that makes use of mutual information in order to measure the amount of information that the fused image contains about the source images. The Matlab code for this metric can be found at.
互信息也用于信号处理领域,用来进行两个信号之间的相似性度量 Similarity measure。例如,FMI 度量是一种利用互信息来度量融合图像包含的关于源图像的信息量的图像融合性能度量。这个度量的 Matlab 代码可以在参考文献[17]中找到。
定向信息 Directed information
Directed information, [math]\displaystyle{ \operatorname{I}\left(X^n \to Y^n\right) }[/math], measures the amount of information that flows from the process [math]\displaystyle{ X^n }[/math] to [math]\displaystyle{ Y^n }[/math], where [math]\displaystyle{ X^n }[/math] denotes the vector [math]\displaystyle{ X_1, X_2, ..., X_n }[/math] and [math]\displaystyle{ Y^n }[/math] denotes [math]\displaystyle{ Y_1, Y_2, ..., Y_n }[/math]. The term directed information was coined by James Massey and is defined as
Directed information, I(𝑋𝑛→𝑌𝑛), measures the amount of information that flows from the process 𝑋𝑛 to 𝑌𝑛, where 𝑋𝑛 denotes the vector 𝑋1,𝑋2,...,𝑋𝑛 and 𝑌𝑛 denotes 𝑌1,𝑌2,...,𝑌𝑛. The term directed information was coined by James Massey and is defined as:
定向信息 Directed information[math]\displaystyle{ \operatorname{I}\left(X^n \to Y^n\right) }[/math]度量从[math]\displaystyle{ X^n }[/math]流向[math]\displaystyle{ Y^n }[/math]的过程中的信息量,其中[math]\displaystyle{ X^n }[/math]表示为向量[math]\displaystyle{ X_1, X_2, ..., X_n }[/math],[math]\displaystyle{ Y^n }[/math]表示为[math]\displaystyle{ Y_1, Y_2, ..., Y_n }[/math]。定向信息这个术语是由 James Massey 创造的,它被定义为:
- [math]\displaystyle{ \operatorname{I}\left(X^n \to Y^n\right) = \sum_{i=1}^n \operatorname{I}\left(X^i; Y_i|Y^{i-1}\right) }[/math].
Note that if [math]\displaystyle{ n=1 }[/math], the directed information becomes the mutual information. Directed information has many applications in problems where causality plays an important role, such as capacity of channel with feedback.[18][19]
Note that if 𝑛=1, the directed information becomes the mutual information. Directed information has many applications in problems where causality plays an important role, such as capacity of channel with feedback.
注意,当[math]\displaystyle{ n=1 }[/math]时,则定向信息成为互信息。定向信息在因果关系问题中有着广泛的应用,如反馈信道容量问题 Channel capacity。
标准化变形 Normalized variants
Normalized variants of the mutual information are provided by the coefficients of constraint,模板:Sfn uncertainty coefficient[20] or proficiency:[21]
Normalized variants of the mutual information are provided by the coefficients of constraint, uncertainty coefficient or proficiency:
互信息的规范化变量由约束系数、不确定系数或熟练程度组成:
- [math]\displaystyle{ C_{XY} = \frac{\operatorname{I}(X;Y)}{H(Y)} ~~~~\mbox{和}~~~~ C_{YX} = \frac{\operatorname{I}(X;Y)}{H(X)}. }[/math]
The two coefficients have a value ranging in [0, 1], but are not necessarily equal. In some cases a symmetric measure may be desired, such as the following redundancy[citation needed] measure:
The two coefficients have a value ranging in [0, 1], but are not necessarily equal. In some cases a symmetric measure may be desired, such as the following redundancy measure:
这两个系数的值范围均为[0,1],但不一定是相等的。在某些情况下,可能需要一个对称的度量,例如下面的冗余度量:
- [math]\displaystyle{ R = \frac{\operatorname{I}(X;Y)}{H(X) + H(Y)} }[/math]
which attains a minimum of zero when the variables are independent and a maximum value of
which attains a minimum of zero when the variables are independent and a maximum value of
当变量是独立的时候,它的最小值为零,最大值可以达到:
- [math]\displaystyle{ R_\max = \frac{\min\left\{H(X), H(Y)\right\}}{H(X) + H(Y)} }[/math]
when one variable becomes completely redundant with the knowledge of the other. See also Redundancy (information theory).
when one variable becomes completely redundant with the knowledge of the other. See also Redundancy (information theory).
当一个变量与另一个变量的知识完全多余时。参见冗余(信息论)。
Another symmetrical measure is the symmetric uncertainty 模板:Harv, given by
Another symmetrical measure is the symmetric uncertainty , given by
另一个对称度量是对称不确定度,由下式表示:
- [math]\displaystyle{ U(X, Y) = 2R = 2\frac{\operatorname{I}(X;Y)}{Ha(X) + H(Y)} }[/math]
which represents the harmonic mean of the two uncertainty coefficients [math]\displaystyle{ C_{XY}, C_{YX} }[/math].[20]
which represents the harmonic mean of the two uncertainty coefficients [math]\displaystyle{ C_{XY}, C_{YX} }[/math].
它表示两个不确定系数的调和平均数。
If we consider mutual information as a special case of the total correlation or dual total correlation, the normalized version are respectively,
If we consider mutual information as a special case of the total correlation or dual total correlation, the normalized version are respectively,
如果我们把互信息看作是总相关 Total correlation或对偶总相关 Dual total correlation的特殊情况,则其标准化版本分别为,
- [math]\displaystyle{ \frac{\operatorname{I}(X;Y)}{\min\left[ H(X),H(Y)\right]} }[/math] and [math]\displaystyle{ \frac{\operatorname{I}(X;Y)}{H(X,Y)} \; . }[/math]
This normalized version also known as Information Quality Ratio (IQR) which quantifies the amount of information of a variable based on another variable against total uncertainty:[22]
This normalized version also known as Information Quality Ratio (IQR) which quantifies the amount of information of a variable based on another variable against total uncertainty:
这个标准化版本也被称为信息质量比率 Information Quality Ratio,IQR ,它根据另一个变量量化了一个变量的信息量,来对抗总的不确定性:
- [math]\displaystyle{ IQR(X, Y) = \operatorname{E}[\operatorname{I}(X;Y)] = \frac{\operatorname{I}(X;Y)}{H(X, Y)} = \frac{\sum_{x \in X} \sum_{y \in Y} p(x, y) \log {p(x)p(y)}}{\sum_{x \in X} \sum_{y \in Y} p(x, y) \log {p(x, y)}} - 1 }[/math]
There's a normalization[23] which derives from first thinking of mutual information as an analogue to covariance (thus Shannon entropy is analogous to variance). Then the normalized mutual information is calculated akin to the Pearson correlation coefficient,
There's a normalization which derives from first thinking of mutual information as an analogue to covariance (thus Shannon entropy is analogous to variance). Then the normalized mutual information is calculated akin to the Pearson correlation coefficient,
有一个标准化的名字——它起源于最初把互信息看作是协方差 Covariance的类比(因此香农熵类似于方差)。然后计算归一化互信息类似于皮尔森相关系数 Pearson product-moment:
- [math]\displaystyle{ \frac{\operatorname{I}(X;Y)}{\sqrt{H(X)H(Y)}}\; . }[/math]
加权变量 Weighted variants
In the traditional formulation of the mutual information,
In the traditional formulation of the mutual information,
在互信息的传统表述中:
- [math]\displaystyle{ \operatorname{I}(X;Y) = \sum_{y \in Y} \sum_{x \in X} p(x, y) \log \frac{p(x, y)}{p(x)\,p(y)}, }[/math]
each event or object specified by [math]\displaystyle{ (x, y) }[/math] is weighted by the corresponding probability [math]\displaystyle{ p(x, y) }[/math]. This assumes that all objects or events are equivalent apart from their probability of occurrence. However, in some applications it may be the case that certain objects or events are more significant than others, or that certain patterns of association are more semantically important than others.
each event or object specified by [math]\displaystyle{ (x, y) }[/math] is weighted by the corresponding probability [math]\displaystyle{ p(x, y) }[/math]. This assumes that all objects or events are equivalent apart from their probability of occurrence. However, in some applications it may be the case that certain objects or events are more significant than others, or that certain patterns of association are more semantically important than others.
Math (x,y) / math 指定的每个事件或对象都由相应的概率 math p (x,y) / math 加权。这假设除了发生概率之外,所有对象或事件都是等效的。然而,在某些应用程序中,某些对象或事件可能比其他对象或事件更重要,或者某些关联模式在语义上比其他模式更重要。
For example, the deterministic mapping [math]\displaystyle{ \{(1,1),(2,2),(3,3)\} }[/math] may be viewed as stronger than the deterministic mapping [math]\displaystyle{ \{(1,3),(2,1),(3,2)\} }[/math], although these relationships would yield the same mutual information. This is because the mutual information is not sensitive at all to any inherent ordering in the variable values (Cronbach 1954, Coombs, Dawes & Tversky 1970, Lockhead 1970), and is therefore not sensitive at all to the form of the relational mapping between the associated variables. If it is desired that the former relation—showing agreement on all variable values—be judged stronger than the later relation, then it is possible to use the following weighted mutual information 模板:Harv.
For example, the deterministic mapping [math]\displaystyle{ \{(1,1),(2,2),(3,3)\} }[/math] may be viewed as stronger than the deterministic mapping [math]\displaystyle{ \{(1,3),(2,1),(3,2)\} }[/math], although these relationships would yield the same mutual information. This is because the mutual information is not sensitive at all to any inherent ordering in the variable values (, , ), and is therefore not sensitive at all to the form of the relational mapping between the associated variables. If it is desired that the former relation—showing agreement on all variable values—be judged stronger than the later relation, then it is possible to use the following weighted mutual information .
例如,确定性映射数学{(1,1) ,(2,2) ,(3,3)} / math 可能被视为比确定性映射数学{(1,3) ,(2,1) ,(3,2)} / math 更强,尽管这些关系将产生相同的互信息。这是因为互信息对变量值(,,)的任何固有顺序都不敏感,因此对相关变量之间的关系映射形式一点也不敏感。如果希望判断前一个关系(即对所有变量值的一致性)比后一个关系强,则可以使用下列加权互信息。
- [math]\displaystyle{ \operatorname{I}(X;Y) = \sum_{y \in Y} \sum_{x \in X} w(x,y) p(x,y) \log \frac{p(x,y)}{p(x)\,p(y)}, }[/math]
which places a weight [math]\displaystyle{ w(x,y) }[/math] on the probability of each variable value co-occurrence, [math]\displaystyle{ p(x,y) }[/math]. This allows that certain probabilities may carry more or less significance than others, thereby allowing the quantification of relevant holistic or Prägnanz factors. In the above example, using larger relative weights for [math]\displaystyle{ w(1,1) }[/math], [math]\displaystyle{ w(2,2) }[/math], and [math]\displaystyle{ w(3,3) }[/math] would have the effect of assessing greater informativeness for the relation [math]\displaystyle{ \{(1,1),(2,2),(3,3)\} }[/math] than for the relation [math]\displaystyle{ \{(1,3),(2,1),(3,2)\} }[/math], which may be desirable in some cases of pattern recognition, and the like. This weighted mutual information is a form of weighted KL-Divergence, which is known to take negative values for some inputs,[24] and there are examples where the weighted mutual information also takes negative values.[25]
which places a weight [math]\displaystyle{ w(x,y) }[/math] on the probability of each variable value co-occurrence, [math]\displaystyle{ p(x,y) }[/math]. This allows that certain probabilities may carry more or less significance than others, thereby allowing the quantification of relevant holistic or Prägnanz factors. In the above example, using larger relative weights for [math]\displaystyle{ w(1,1) }[/math], [math]\displaystyle{ w(2,2) }[/math], and [math]\displaystyle{ w(3,3) }[/math] would have the effect of assessing greater informativeness for the relation [math]\displaystyle{ \{(1,1),(2,2),(3,3)\} }[/math] than for the relation [math]\displaystyle{ \{(1,3),(2,1),(3,2)\} }[/math], which may be desirable in some cases of pattern recognition, and the like. This weighted mutual information is a form of weighted KL-Divergence, which is known to take negative values for some inputs, and there are examples where the weighted mutual information also takes negative values.
将权重 math w (x,y) / math 放在每个变量值共现的概率上,math p (x,y) / math。这使得某些概率可能比其他概率具有更多或更少的重要性,从而允许量化相关的整体因子或 pr gnaanz 因子。在上面的例子中,对数学 w (1,1) / math,math w (2,2) / math,和 math w (3,3) / math 使用较大的相对权重,对关系数学 w (1,1) ,(2,2) ,(3,3) / math 比对关系数学 w (1,3) ,(2,1) ,(3,2) / math 有更大的信息量,这在某些模式识别的情况下是可取的,等等。这种加权互信息是加权的 kl 散度的一种形式,已知它对某些输入取负值,有些例子中加权互信息也取负值。
调整后的互信息 Adjusted mutual information
A probability distribution can be viewed as a partition of a set. One may then ask: if a set were partitioned randomly, what would the distribution of probabilities be? What would the expectation value of the mutual information be? The adjusted mutual information or AMI subtracts the expectation value of the MI, so that the AMI is zero when two different distributions are random, and one when two distributions are identical. The AMI is defined in analogy to the adjusted Rand index of two different partitions of a set.
A probability distribution can be viewed as a partition of a set. One may then ask: if a set were partitioned randomly, what would the distribution of probabilities be? What would the expectation value of the mutual information be? The adjusted mutual information or AMI subtracts the expectation value of the MI, so that the AMI is zero when two different distributions are random, and one when two distributions are identical. The AMI is defined in analogy to the adjusted Rand index of two different partitions of a set.
概率分布可以被看作是集合划分。然后有人可能会问: 如果一个集合被随机分割,概率的分布会是什么?相互信息的期望值是什么?调整后的互信息或 AMI 减去 MI 的期望值,因此当两个不同的分布是随机的时候 AMI 为零,当两个分布是相同的时候 AMI 为零。Ami 的定义类似于一个集合的两个不同分区的调整后的 Rand 指数。
绝对互信息 Absolute mutual information
Using the ideas of Kolmogorov complexity, one can consider the mutual information of two sequences independent of any probability distribution:
Using the ideas of Kolmogorov complexity, one can consider the mutual information of two sequences independent of any probability distribution:
利用柯氏复杂性的思想,我们可以考虑两个序列的互信息,这两个序列独立于任何概率分布序列:
- [math]\displaystyle{ \operatorname{I}_K(X;Y) = K(X) - K(X|Y). }[/math]
To establish that this quantity is symmetric up to a logarithmic factor ([math]\displaystyle{ \operatorname{I}_K(X;Y) \approx \operatorname{I}_K(Y;X) }[/math]) one requires the chain rule for Kolmogorov complexity {{ |bracket_left= ( |bracket_right = ) }}. Approximations of this quantity via compression can be used to define a distance measure to perform a hierarchical clustering of sequences without having any domain knowledge of the sequences {{ |bracket_left= ( |bracket_right = ) }}.
To establish that this quantity is symmetric up to a logarithmic factor ([math]\displaystyle{ \operatorname{I}_K(X;Y) \approx \operatorname{I}_K(Y;X) }[/math]) one requires the chain rule for Kolmogorov complexity . Approximations of this quantity via compression can be used to define a distance measure to perform a hierarchical clustering of sequences without having any domain knowledge of the sequences .
为了证明这个量对称于一个对数因子(math operatorname { i } k (x; y) approx operatorname { i } k (y; x) / math) ,我们需要一个柯氏复杂性的链式规则。通过压缩这个量的近似值可以用来定义一个距离度量来执行一个层次化的序列聚类,而不需要任何关于序列的领域知识。
线性相关 Linear correlation
Unlike correlation coefficients, such as the product moment correlation coefficient, mutual information contains information about all dependence—linear and nonlinear—and not just linear dependence as the correlation coefficient measures. However, in the narrow case that the joint distribution for [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] is a bivariate normal distribution (implying in particular that both marginal distributions are normally distributed), there is an exact relationship between [math]\displaystyle{ \operatorname{I} }[/math] and the correlation coefficient [math]\displaystyle{ \rho }[/math] 模板:Harv.
Unlike correlation coefficients, such as the product moment correlation coefficient, mutual information contains information about all dependence—linear and nonlinear—and not just linear dependence as the correlation coefficient measures. However, in the narrow case that the joint distribution for [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] is a bivariate normal distribution (implying in particular that both marginal distributions are normally distributed), there is an exact relationship between [math]\displaystyle{ \operatorname{I} }[/math] and the correlation coefficient [math]\displaystyle{ \rho }[/math] .
互信息不同于相关系数,如乘积矩相关系数,互信息包含所有相关信息ーー线性和非线性ーー而不仅仅是相关系数的线性相关。然而,在数学 x / math 和数学 y / math 的联合分布是二元正态分布(特别是边际分布都是正态分布)的狭义情况下,数学运算子{ i } / math 与相关系数 math / rho / math 之间存在精确的关系。
- [math]\displaystyle{ \operatorname{I} = -\frac{1}{2} \log\left(1 - \rho^2\right) }[/math]
The equation above can be derived as follows for a bivariate Gaussian:
The equation above can be derived as follows for a bivariate Gaussian:
对于双变量高斯分布,上面的公式可以推导如下:
- [math]\displaystyle{ \begin{align} \begin{pmatrix} X_1 \\ X_2 \end{pmatrix} &\sim \mathcal{N} \left( \begin{pmatrix} \mu_1 \\ \mu_2 \end{pmatrix}, \Sigma \right),\qquad \Sigma = \begin{pmatrix} \sigma^2_1 & \rho\sigma_1\sigma_2 \\ \rho\sigma_1\sigma_2 & \sigma^2_2 \end{pmatrix} \\ H(X_i) &= \frac{1}{2}\log\left(2\pi e \sigma_i^2\right) = \frac{1}{2} + \frac{1}{2}\log(2\pi) + \log\left(\sigma_i\right), \quad i\in\{1, 2\} \\ H(X_1, X_2) &= \frac{1}{2}\log\left[(2\pi e)^2|\Sigma|\right] = 1 + \log(2\pi) + \log\left(\sigma_1 \sigma_2\right) + \frac{1}{2}\log\left(1 - \rho^2\right) \\ \end{align} }[/math]
Therefore,
Therefore,
所以,
- [math]\displaystyle{ \operatorname{I}\left(X_1; X_2\right) = H\left(X_1\right) + H\left(X_2\right) - H\left(X_1, X_2\right) = -\frac{1}{2}\log\left(1 - \rho^2\right) }[/math]
对于离散数据 For discrete data
When [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] are limited to be in a discrete number of states, observation data is summarized in a contingency table, with row variable [math]\displaystyle{ X }[/math] (or [math]\displaystyle{ i }[/math]) and column variable [math]\displaystyle{ Y }[/math] (or [math]\displaystyle{ j }[/math]). Mutual information is one of the measures of association or correlation between the row and column variables. Other measures of association include Pearson's chi-squared test statistics, G-test statistics, etc. In fact, mutual information is equal to G-test statistics divided by [math]\displaystyle{ 2N }[/math], where [math]\displaystyle{ N }[/math] is the sample size.
When [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] are limited to be in a discrete number of states, observation data is summarized in a contingency table, with row variable [math]\displaystyle{ X }[/math] (or [math]\displaystyle{ i }[/math]) and column variable [math]\displaystyle{ Y }[/math] (or [math]\displaystyle{ j }[/math]). Mutual information is one of the measures of association or correlation between the row and column variables. Other measures of association include Pearson's chi-squared test statistics, G-test statistics, etc. In fact, mutual information is equal to G-test statistics divided by [math]\displaystyle{ 2N }[/math], where [math]\displaystyle{ N }[/math] is the sample size.
当数学 x / 数学和数学 y / 数学被限制在一个离散的数字状态时,观察数据被总结成一个列联表,有行变量 math x / math (或 math i / math)和列变量 math y / math (或 math j / math)。互信息是行变量和列变量之间关联或相关性的度量之一。其他衡量相关性的指标包括皮尔森卡方检验统计数据、 g 测试统计数据等。事实上,互信息等于 g 检验统计除以 math 2N / math,其中 math n / math 是样本量。
应用 Applications
In many applications, one wants to maximize mutual information (thus increasing dependencies), which is often equivalent to minimizing conditional entropy. Examples include:
In many applications, one wants to maximize mutual information (thus increasing dependencies), which is often equivalent to minimizing conditional entropy. Examples include:
在许多应用程序中,需要最大化互信息(从而增加依赖关系) ,这通常相当于最小化条件熵。例如:
- In search engine technology, mutual information between phrases and contexts is used as a feature for k-means clustering to discover semantic clusters (concepts).[26] For example, the mutual information of a bigram might be calculated as:
[math]\displaystyle{ MI(x,y) = \log \frac{P_{X,Y}(x,y)}{P_X(x) P_Y(y)} \approx log \frac{\frac{f_{XY}}{B}}{\frac{f_X}{U} \frac{f_Y}{U}} }[/math]
where [math]\displaystyle{ f_{XY} }[/math] is the number of times the bigram xy appears in the corpus, [math]\displaystyle{ f_{X} }[/math] is the number of times the unigram x appears in the corpus, B is the total number of bigrams, and U is the total number of unigrams.[26]
where [math]\displaystyle{ f_{XY} }[/math] is the number of times the bigram xy appears in the corpus, [math]\displaystyle{ f_{X} }[/math] is the number of times the unigram x appears in the corpus, B is the total number of bigrams, and U is the total number of unigrams.
其中 math f { XY } / math 是 bigram XY 在语料库中出现的次数,math f { x } / math 是 unigram x 在语料库中出现的次数,b 是 bigrams 的总数,u 是 unigrams 的总数。
- In telecommunications, the channel capacity is equal to the mutual information, maximized over all input distributions.
- Discriminative training procedures for hidden Markov models have been proposed based on the maximum mutual information (MMI) criterion.
- RNA secondary structure prediction from a multiple sequence alignment.
- Phylogenetic profiling prediction from pairwise present and disappearance of functionally link genes.
- Mutual information has been used as a criterion for feature selection and feature transformations in machine learning. It can be used to characterize both the relevance and redundancy of variables, such as the minimum redundancy feature selection.
- Mutual information is used in determining the similarity of two different clusterings of a dataset. As such, it provides some advantages over the traditional Rand index.
- Mutual information of words is often used as a significance function for the computation of collocations in corpus linguistics. This has the added complexity that no word-instance is an instance to two different words; rather, one counts instances where 2 words occur adjacent or in close proximity; this slightly complicates the calculation, since the expected probability of one word occurring within [math]\displaystyle{ N }[/math] words of another, goes up with [math]\displaystyle{ N }[/math].
- Mutual information is used in medical imaging for image registration. Given a reference image (for example, a brain scan), and a second image which needs to be put into the same coordinate system as the reference image, this image is deformed until the mutual information between it and the reference image is maximized.
- Detection of phase synchronization in time series analysis
- In the infomax method for neural-net and other machine learning, including the infomax-based Independent component analysis algorithm
- Average mutual information in delay embedding theorem is used for determining the embedding delay parameter.
- Mutual information between genes in expression microarray data is used by the ARACNE algorithm for reconstruction of gene networks.
- In statistical mechanics, Loschmidt's paradox may be expressed in terms of mutual information.[27][28] Loschmidt noted that it must be impossible to determine a physical law which lacks time reversal symmetry (e.g. the second law of thermodynamics) only from physical laws which have this symmetry. He pointed out that the H-theorem of Boltzmann made the assumption that the velocities of particles in a gas were permanently uncorrelated, which removed the time symmetry inherent in the H-theorem. It can be shown that if a system is described by a probability density in phase space, then Liouville's theorem implies that the joint information (negative of the joint entropy) of the distribution remains constant in time. The joint information is equal to the mutual information plus the sum of all the marginal information (negative of the marginal entropies) for each particle coordinate. Boltzmann's assumption amounts to ignoring the mutual information in the calculation of entropy, which yields the thermodynamic entropy (divided by Boltzmann's constant).
- The mutual information is used to learn the structure of Bayesian networks/dynamic Bayesian networks, which is thought to explain the causal relationship between random variables, as exemplified by the GlobalMIT toolkit:[29] learning the globally optimal dynamic Bayesian network with the Mutual Information Test criterion.
- Popular cost function in decision tree learning.
- The mutual information is used in cosmology to test the influence of large-scale environments on galaxy properties in the Galaxy Zoo.
- The mutual information was used in Solar Physics to derive the solar differential rotation profile, a travel-time deviation map for sunspots, and a time–distance diagram from quiet-Sun measurements[30]
- Used in Invariant Information Clustering to automatically train neural network classifiers and image segmenters given no labelled data.[31]
参见 See also
注释 Notes
- ↑ 1.0 1.1 1.2 Cover, T.M.; Thomas, J.A. (1991). Elements of Information Theory (Wiley ed.). ISBN 978-0-471-24195-9. https://archive.org/details/elementsofinform0000cove.
- ↑ Wolpert, D.H.; Wolf, D.R. (1995). "Estimating functions of probability distributions from a finite set of samples". Physical Review E. 52 (6): 6841–6854. Bibcode:1995PhRvE..52.6841W. CiteSeerX 10.1.1.55.7122. doi:10.1103/PhysRevE.52.6841. PMID 9964199.
- ↑ Hutter, M. (2001). "Distribution of Mutual Information". Advances in Neural Information Processing Systems 2001.
- ↑ Archer, E.; Park, I.M.; Pillow, J. (2013). "Bayesian and Quasi-Bayesian Estimators for Mutual Information from Discrete Data". Entropy. 15 (12): 1738–1755. Bibcode:2013Entrp..15.1738A. CiteSeerX 10.1.1.294.4690. doi:10.3390/e15051738.
- ↑ Wolpert, D.H; DeDeo, S. (2013). "Estimating Functions of Distributions Defined over Spaces of Unknown Size". Entropy. 15 (12): 4668–4699. arXiv:1311.4548. Bibcode:2013Entrp..15.4668W. doi:10.3390/e15114668.
- ↑ Tomasz Jetka; Karol Nienaltowski; Tomasz Winarski; Slawomir Blonski; Michal Komorowski (2019), "Information-theoretic analysis of multivariate single-cell signaling responses", PLOS Computational Biology, 15 (7): e1007132, arXiv:1808.05581, Bibcode:2019PLSCB..15E7132J, doi:10.1371/journal.pcbi.1007132, PMC 6655862, PMID 31299056
- ↑ Kraskov, Alexander; Stögbauer, Harald; Andrzejak, Ralph G.; Grassberger, Peter (2003). "Hierarchical Clustering Based on Mutual Information". arXiv:q-bio/0311039. Bibcode:2003q.bio....11039K.
{{cite journal}}: Cite journal requires|journal=(help) - ↑ McGill, W. (1954). "Multivariate information transmission". Psychometrika. 19 (1): 97–116. doi:10.1007/BF02289159.
- ↑ Hu, K.T. (1962). "On the Amount of Information". Theory Probab. Appl. 7 (4): 439–447. doi:10.1137/1107041.
- ↑ 10.0 10.1 10.2 Baudot, P.; Tapia, M.; Bennequin, D.; Goaillard, J.M. (2019). "Topological Information Data Analysis". Entropy. 21 (9). 869. arXiv:1907.04242. Bibcode:2019Entrp..21..869B. doi:10.3390/e21090869.
- ↑ Brenner, N.; Strong, S.; Koberle, R.; Bialek, W. (2000). "Synergy in a Neural Code". Neural Comput. 12 (7): 1531–1552. doi:10.1162/089976600300015259. PMID 10935917.
- ↑ Watkinson, J.; Liang, K.; Wang, X.; Zheng, T.; Anastassiou, D. (2009). "Inference of Regulatory Gene Interactions from Expression Data Using Three-Way Mutual Information". Chall. Syst. Biol. Ann. N. Y. Acad. Sci. 1158 (1): 302–313. Bibcode:2009NYASA1158..302W. doi:10.1111/j.1749-6632.2008.03757.x. PMID 19348651.
- ↑ 13.0 13.1 Tapia, M.; Baudot, P.; Formizano-Treziny, C.; Dufour, M.; Goaillard, J.M. (2018). "Neurotransmitter identity and electrophysiological phenotype are genetically coupled in midbrain dopaminergic neurons". Sci. Rep. 8 (1): 13637. Bibcode:2018NatSR...813637T. doi:10.1038/s41598-018-31765-z. PMC 6134142. PMID 30206240.
- ↑ Hu, K.T. (1962). "On the Amount of Information". Theory Probab. Appl. 7 (4): 439–447. doi:10.1137/1107041.
- ↑ Christopher D. Manning; Prabhakar Raghavan; Hinrich Schütze (2008). An Introduction to Information Retrieval. Cambridge University Press. ISBN 978-0-521-86571-5.
- ↑ Haghighat, M. B. A.; Aghagolzadeh, A.; Seyedarabi, H. (2011). "A non-reference image fusion metric based on mutual information of image features". Computers & Electrical Engineering. 37 (5): 744–756. doi:10.1016/j.compeleceng.2011.07.012.
- ↑ "Feature Mutual Information (FMI) metric for non-reference image fusion - File Exchange - MATLAB Central". www.mathworks.com. Retrieved 4 April 2018.
- ↑ Massey, James (1990). "Causality, Feedback And Directed Informatio". Proc. 1990 Intl. Symp. on Info. Th. and its Applications, Waikiki, Hawaii, Nov. 27-30, 1990. CiteSeerX 10.1.1.36.5688.
- ↑ Permuter, Haim Henry; Weissman, Tsachy; Goldsmith, Andrea J. (February 2009). "Finite State Channels With Time-Invariant Deterministic Feedback". IEEE Transactions on Information Theory. 55 (2): 644–662. arXiv:cs/0608070. doi:10.1109/TIT.2008.2009849.
- ↑ 20.0 20.1 Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007). "Section 14.7.3. Conditional Entropy and Mutual Information". Numerical Recipes: The Art of Scientific Computing (3rd ed.). New York: Cambridge University Press. ISBN 978-0-521-88068-8. http://apps.nrbook.com/empanel/index.html#pg=758.
- ↑ White, Jim; Steingold, Sam; Fournelle, Connie. Performance Metrics for Group-Detection Algorithms (PDF). Interface 2004.
- ↑ Wijaya, Dedy Rahman; Sarno, Riyanarto; Zulaika, Enny (2017). "Information Quality Ratio as a novel metric for mother wavelet selection". Chemometrics and Intelligent Laboratory Systems. 160: 59–71. doi:10.1016/j.chemolab.2016.11.012.
- ↑ Strehl, Alexander; Ghosh, Joydeep (2003). "Cluster Ensembles – A Knowledge Reuse Framework for Combining Multiple Partitions" (PDF). The Journal of Machine Learning Research. 3: 583–617. doi:10.1162/153244303321897735.
- ↑ Kvålseth, T. O. (1991). "The relative useful information measure: some comments". Information Sciences. 56 (1): 35–38. doi:10.1016/0020-0255(91)90022-m.
- ↑ 模板:Cite dissertation
- ↑ 26.0 26.1 Parsing a Natural Language Using Mutual Information Statistics by David M. Magerman and Mitchell P. Marcus
- ↑ Hugh Everett Theory of the Universal Wavefunction, Thesis, Princeton University, (1956, 1973), pp 1–140 (page 30)
- ↑ Everett, Hugh (1957). "Relative State Formulation of Quantum Mechanics". Reviews of Modern Physics. 29 (3): 454–462. Bibcode:1957RvMP...29..454E. doi:10.1103/revmodphys.29.454. Archived from the original on 2011-10-27. Retrieved 2012-07-16.
- ↑ 模板:Google Code
- ↑ Keys, Dustin; Kholikov, Shukur; Pevtsov, Alexei A. (February 2015). "Application of Mutual Information Methods in Time Distance Helioseismology". Solar Physics. 290 (3): 659–671. arXiv:1501.05597. Bibcode:2015SoPh..290..659K. doi:10.1007/s11207-015-0650-y.
- ↑ Invariant Information Clustering for Unsupervised Image Classification and Segmentation by Xu Ji, Joao Henriques and Andrea Vedaldi
参考资料 References
- Baudot, P.; Tapia, M.; Bennequin, D.; Goaillard, J.M. (2019). "Topological Information Data Analysis". Entropy. 21 (9). 869. arXiv:1907.04242. Bibcode:2019Entrp..21..869B. doi:10.3390/e21090869.
- Cilibrasi
1塞利布拉西, R.
1 r.; Vitányi, Paul (2005
2005年). [http://www.cwi.nl/~paulv/papers/cluster.pdf
Http://www.cwi.nl/~paulv/papers/cluster.pdf "Clustering by compression 压缩聚类"] (PDF). IEEE Transactions on Information Theory 美国电气和电子工程师协会信息理论杂志. 51
第51卷 (4
第四期): 1523–1545
第1523-1545页. arXiv:cs/0312044. doi:[//doi.org/10.1109%2FTIT.2005.844059%0A%0A10.1109%20%2F%20TIT.%202005.844059 10.1109/TIT.2005.844059
10.1109 / TIT. 2005.844059]. {{cite journal}}: Check |doi= value (help); Check |url= value (help); Check date values in: |year= (help); Text "first2保罗" ignored (help); line feed character in |doi= at position 24 (help); line feed character in |first1= at position 3 (help); line feed character in |issue= at position 2 (help); line feed character in |journal= at position 40 (help); line feed character in |last1= at position 10 (help); line feed character in |pages= at position 10 (help); line feed character in |ref= at position 5 (help); line feed character in |title= at position 26 (help); line feed character in |url= at position 44 (help); line feed character in |volume= at position 3 (help); line feed character in |year= at position 5 (help)
}}
}}
- Cronbach, L. J. (1954). "On the non-rational application of information measures in psychology". In Quastler, Henry. Information Theory in Psychology: Problems and Methods. Glencoe, Illinois: Free Press. pp. 14–30.
- Coombs, C. H.; Dawes, R. M.; Tversky, A. (1970). Mathematical Psychology: An Elementary Introduction. Englewood Cliffs, New Jersey: Prentice-Hall.
- Church, Kenneth Ward; Hanks, Patrick (1989). "Word association norms, mutual information, and lexicography". Proceedings of the 27th Annual Meeting of the Association for Computational Linguistics: 76–83. doi:10.3115/981623.981633.
- Gel'fand, I.M.; Yaglom, A.M. (1957). "Calculation of amount of information about a random function contained in another such function". American Mathematical Society Translations: Series 2. 12: 199–246.
{{cite journal}}: Invalid|ref=harv(help) English translation of original in Uspekhi Matematicheskikh Nauk 12 (1): 3-52.
- Guiasu, Silviu (1977). Information Theory with Applications. McGraw-Hill, New York. ISBN 978-0-07-025109-0.
- Li
最后一个李, Ming
1 Ming; Vitányi, Paul (February 1997
1997年2月). An introduction to Kolmogorov complexity and its applications
标题: 柯氏复杂性及其应用介绍. New York: Springer-Verlag. ISBN [[Special:BookSources/978-0-387-94868-3
[国际标准图书编号978-0-387-94868-3]|978-0-387-94868-3
[国际标准图书编号978-0-387-94868-3]]].
| ref=harv }}
| ref harv }
- Lockhead, G. R. (1970). "Identification and the form of multidimensional discrimination space". Journal of Experimental Psychology. 85 (1): 1–10. doi:10.1037/h0029508. PMID 5458322.
{{cite journal}}: Invalid|ref=harv(help)
- David J. C. MacKay. Information Theory, Inference, and Learning Algorithms Cambridge: Cambridge University Press, 2003. (available free online)
- Haghighat, M. B. A.; Aghagolzadeh, A.; Seyedarabi, H. (2011). "A non-reference image fusion metric based on mutual information of image features". Computers & Electrical Engineering. 37 (5): 744–756. doi:10.1016/j.compeleceng.2011.07.012.
- Athanasios Papoulis. Probability, Random Variables, and Stochastic Processes, second edition. New York: McGraw-Hill, 1984. (See Chapter 15.)
- Witten, Ian H. & Frank, Eibe (2005). Data Mining: Practical Machine Learning Tools and Techniques. Morgan Kaufmann, Amsterdam. ISBN 978-0-12-374856-0. http://www.cs.waikato.ac.nz/~ml/weka/book.html.
- Peng, H.C.; Long, F.; Ding, C. (2005). "Feature selection based on mutual information: criteria of max-dependency, max-relevance, and min-redundancy". IEEE Transactions on Pattern Analysis and Machine Intelligence. 27 (8): 1226–1238. CiteSeerX 10.1.1.63.5765. doi:10.1109/tpami.2005.159. PMID 16119262.
{{cite journal}}: Unknown parameter|lastauthoramp=ignored (help)
- Andre S. Ribeiro; Stuart A. Kauffman; Jason Lloyd-Price; Bjorn Samuelsson; Joshua Socolar (2008). "Mutual Information in Random Boolean models of regulatory networks". Physical Review E. 77 (1): 011901. arXiv:0707.3642. Bibcode:2008PhRvE..77a1901R. doi:10.1103/physreve.77.011901. PMID 18351870.
{{cite journal}}: Unknown parameter|last-author-amp=ignored (help)
- Wells
1 Wells, W.M. III
首先是 w.m。三; Viola
2 Viola, P.; Atsumi
3 Atsumi, H.
第一个3 h。; Nakajima, S.
4 s.; Kikinis
最后5个 Kikinis, R. (1996
1996年). "Multi-modal volume registration by maximization of mutual information 最大化互信息的多模态卷注册" (PDF). Medical Image Analysis 医学图像分析. 1
第一卷 (1
第一期): 35–51
第35-51页. doi:10.1016/S1361-8415(01)80004-9. PMID [//pubmed.ncbi.nlm.nih.gov/9873920
9873920 9873920 9873920]. Archived from [http://www.ai.mit.edu/people/sw/papers/mia.pdf
Http://www.ai.mit.edu/people/sw/papers/mia.pdf the original] (PDF) on 2008-09-06
2008-09-06. Retrieved 2010-08-05
2010-08-05.
{{cite journal}}: Check|pmid=value (help); Check|url=value (help); Check date values in:|access-date=,|year=, and|archive-date=(help); Invalid|url-status=dead状态死机(help); Text "doi 10.1016 / S1361-8415(01)80004-9" ignored (help); Text "first2 p." ignored (help); Text "first5 r." ignored (help); Text "最后4名中岛" ignored (help); Text "档案-网址 https://web.archive.org/web/20080906201633/http://www.ai.mit.edu/people/sw/papers/mia.pdf" ignored (help); line feed character in|access-date=at position 11 (help); line feed character in|archive-date=at position 11 (help); line feed character in|first1=at position 9 (help); line feed character in|first3=at position 3 (help); line feed character in|first4=at position 3 (help); line feed character in|issue=at position 2 (help); line feed character in|journal=at position 23 (help); line feed character in|last1=at position 6 (help); line feed character in|last2=at position 6 (help); line feed character in|last3=at position 7 (help); line feed character in|last5=at position 8 (help); line feed character in|pages=at position 6 (help); line feed character in|pmid=at position 8 (help); line feed character in|ref=at position 5 (help); line feed character in|title=at position 70 (help); line feed character in|url-status=at position 5 (help); line feed character in|url=at position 47 (help); line feed character in|volume=at position 2 (help); line feed character in|year=at position 5 (help)}}
}}
- Pandey, Biswajit; Sarkar, Suman (2017). "How much a galaxy knows about its large-scale environment?: An information theoretic perspective". Monthly Notices of the Royal Astronomical Society Letters. 467 (1): L6. arXiv:1611.00283. Bibcode:2017MNRAS.467L...6P. doi:10.1093/mnrasl/slw250.
Category:Information theory
范畴: 信息论
Category:Entropy and information
类别: 熵和信息
This page was moved from wikipedia:en:Mutual information. Its edit history can be viewed at 互信息/edithistory
- 调用重复模板参数的页面
- CS1 errors: missing periodical
- 含有受损文件链接的页面
- Articles with hatnote templates targeting a nonexistent page
- All articles with unsourced statements
- Articles with unsourced statements from July 2008
- Articles with invalid date parameter in template
- CS1 errors: unrecognized parameter
- CS1 errors: invisible characters
- CS1 errors: dates
- CS1 errors: DOI
- CS1 errors: URL
- CS1: long volume value
- CS1 errors: invalid parameter value
- CS1 errors: unsupported parameter
- CS1 errors: PMID
- Information theory
- Entropy and information
- 待整理页面