“团(图论)”的版本间的差异
| 第189行: | 第189行: | ||
The word "clique", in its graph-theoretic usage, arose from the work of , who used complete subgraphs to model cliques (groups of people who all know each other) in social networks. The same definition was used by in an article using less technical terms. Both works deal with uncovering cliques in a social network using matrices. For continued efforts to model social cliques graph-theoretically, see e.g. , , and . | The word "clique", in its graph-theoretic usage, arose from the work of , who used complete subgraphs to model cliques (groups of people who all know each other) in social networks. The same definition was used by in an article using less technical terms. Both works deal with uncovering cliques in a social network using matrices. For continued efforts to model social cliques graph-theoretically, see e.g. , , and . | ||
| − | + | “团clique”一词在图形理论上的使用,来源于Luce&Perry(1949)的研究《A method of matrix analysis of group structure》,他们通过完全子图对社交网络中的集团(彼此认识的人群)进行建模。之后Festinger(1949)在较少术语的文章《The analysis of sociograms using matrix algebra》中使用了相同的定义。这两部作品都通过使用矩阵的方法来在社交网络中处理团发现问题。之后,Alba(1973),Peay(1974)和Doreian&Woodard(1994)以图理论为基础对社交团体继续进行了图形化建模。 | |
| 第214行: | 第214行: | ||
在化学上,Rhodes等学者(2003年)使用团来描述化学数据库中与目标结构具有高度相似性的化学物质。Kuhl,Crippen&Friesen(1983)使用团对两种化学物质相互结合的位置进行建模。 | 在化学上,Rhodes等学者(2003年)使用团来描述化学数据库中与目标结构具有高度相似性的化学物质。Kuhl,Crippen&Friesen(1983)使用团对两种化学物质相互结合的位置进行建模。 | ||
| − | |||
| − | |||
== See also 其他参考资料 == | == See also 其他参考资料 == | ||
2020年8月24日 (一) 16:10的版本
此词条由Jie初步翻译。
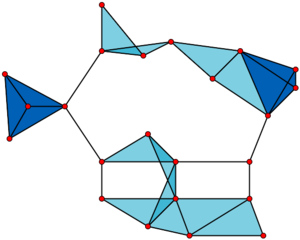
In the mathematical area of graph theory, a clique (模板:IPAc-en or 模板:IPAc-en) is a subset of vertices of an undirected graph such that every two distinct vertices in the clique are adjacent; that is, its induced subgraph is complete. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs. Cliques have also been studied in computer science: the task of finding whether there is a clique of a given size in a graph (the clique problem) is NP-complete, but despite this hardness result, many algorithms for finding cliques have been studied.
In the mathematical area of graph theory, a clique ( or ) is a subset of vertices of an undirected graph such that every two distinct vertices in the clique are adjacent; that is, its induced subgraph is complete. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs. Cliques have also been studied in computer science: the task of finding whether there is a clique of a given size in a graph (the clique problem) is NP-complete, but despite this hardness result, many algorithms for finding cliques have been studied.
在图论的数学领域中, 团Clique是无向图中顶点的子集,使得一个团中每两个不同的顶点必定相邻。也就是说,其导出子图是完全图。团是图论的基本概念之一,可用于图形的构建和解决许多其他数学问题。而且,在计算机科学领域中也经常会涉及到团的研究:比如在一个给定规模的图中寻找团的存在就是一个NP-完全问题。尽管我们已经明确知道这个问题很难得以解决,但仍然有许多学者在研究用于寻找团的算法。
Although the study of complete subgraphs goes back at least to the graph-theoretic reformulation of Ramsey theory by Erdős & Szekeres (1935),[1] the term clique comes from Luce & Perry (1949), who used complete subgraphs in social networks to model cliques of people; that is, groups of people all of whom know each other. Cliques have many other applications in the sciences and particularly in bioinformatics.
Although the study of complete subgraphs goes back at least to the graph-theoretic reformulation of Ramsey theory by , the term clique comes from , who used complete subgraphs in social networks to model cliques of people; that is, groups of people all of whom know each other. Cliques have many other applications in the sciences and particularly in bioinformatics.
对完全子图的研究至少可以追溯到拉姆齐定理中的图论重组,由Erdős&Szekeres(1935)在论文《A combinatorial problem in geometry》提出的。但实际上“团”一词是来自Luce&Perry(1949)的文章《A method of matrix analysis of group structure》,后者在社交网络中使用完全子图来对人群进行建模;该模型定义在这群人中,所有人是互相认识的。其实团这一概念在诸多科学领域中均有所应用,尤其是在生物信息学。
Definitions 定义
A clique, C, in an undirected graph G = (V, E) is a subset of the vertices, C ⊆ V, such that every two distinct vertices are adjacent. This is equivalent to the condition that the induced subgraph of G induced by C is a complete graph. In some cases, the term clique may also refer to the subgraph directly.
A clique, C, in an undirected graph (V, E)}} is a subset of the vertices, , such that every two distinct vertices are adjacent. This is equivalent to the condition that the induced subgraph of G induced by C is a complete graph. In some cases, the term clique may also refer to the subgraph directly.
在一个无向图G =(V,E)中,团C是顶点V的子集,记作:C⊆V,使得每两个不同的顶点相邻。因此团C可以看作是该无向图G的导出子集,进而将此过程视为由C引导出的完全子集的成立条件。在某些情况下,“团”这一术语也可以直接被引用为子集。
A maximal clique is a clique that cannot be extended by including one more adjacent vertex, that is, a clique which does not exist exclusively within the vertex set of a larger clique. Some authors define cliques in a way that requires them to be maximal, and use other terminology for complete subgraphs that are not maximal.
A maximal clique is a clique that cannot be extended by including one more adjacent vertex, that is, a clique which does not exist exclusively within the vertex set of a larger clique. Some authors define cliques in a way that requires them to be maximal, and use other terminology for complete subgraphs that are not maximal.
极大团Maximal clique也是一个团,但是该团不能通过合并更多的相邻节点而进行扩张,换句话说,该团不可能被更大的团所包含。有些学者将“极大团”定义为“团”,而建议用其他术语来重新定义“非极大团”。
A maximum clique of a graph, G, is a clique, such that there is no clique with more vertices. Moreover, the clique number ω(G) of a graph G is the number of vertices in a maximum clique in G.
A maximum clique of a graph, G, is a clique, such that there is no clique with more vertices. Moreover, the clique number ω(G) of a graph G is the number of vertices in a maximum clique in G.
图G中同样存在一个 最大团Maximum clique,使得其不存在更多顶点。另外,图G的团数ω(G)是该图最大团的顶点数。
The intersection number of G is the smallest number of cliques that together cover all edges of G.
The intersection number of G is the smallest number of cliques that together cover all edges of G.
图G的 交叉数Intersection number是该图中能覆盖所有连边的最少团数。
The clique cover number of a graph G is the smallest number of cliques of G whose union covers the set of vertices V of the graph.
The clique cover number of a graph G is the smallest number of cliques of G whose union covers the set of vertices V of the graph.
图G的 团覆盖数Clique cover number指的是能覆盖图G中所有顶点集V的最小团个数。
A maximum clique transversal of a graph is a subset of vertices with the property that each maximum clique of the graph contains at least one vertex in the subset.模板:Sfnp
A maximum clique transversal of a graph is a subset of vertices with the property that each maximum clique of the graph contains at least one vertex in the subset.
一个图的 最大团横贯集Maximum clique transversal是其顶点的子集,其属性为该图的每个最大团中至少有一个顶点在最大团横贯集中。
The opposite of a clique is an independent set, in the sense that every clique corresponds to an independent set in the complement graph. The clique cover problem concerns finding as few cliques as possible that include every vertex in the graph.
The opposite of a clique is an independent set, in the sense that every clique corresponds to an independent set in the complement graph. The clique cover problem concerns finding as few cliques as possible that include every vertex in the graph.
作为团的对立面, 独立集Independent set的存在是指图中两两互相不相邻的顶点集合。因此,每一个团都对应于补图中的独立集。集团覆盖问题涉及到寻找尽可能少的团,其中就包括图中的每个顶点。
A related concept is a biclique, a complete bipartite subgraph. The bipartite dimension of a graph is the minimum number of bicliques needed to cover all the edges of the graph.
A related concept is a biclique, a complete bipartite subgraph. The bipartite dimension of a graph is the minimum number of bicliques needed to cover all the edges of the graph.
二元团biclique是团的相关概念,指的是一个完全二分图。该图的二分维度指的是覆盖该图所有连边的最少二元团数。
Mathematics 数学运算
Mathematical results concerning cliques include the following. Mathematical results concerning cliques include the following. 有关团的数学结论包括以下内容。
- Turán's theorem gives a lower bound on the size of a clique in dense graphs.模板:Sfnp If a graph has sufficiently many edges, it must contain a large clique. For instance, every graph with [math]\displaystyle{ n }[/math] vertices and more than [math]\displaystyle{ \scriptstyle\lfloor\frac{n}{2}\rfloor\cdot\lceil\frac{n}{2}\rceil }[/math] edges must contain a three-vertex clique.
- Ramsey's theorem states that every graph or its complement graph contains a clique with at least a logarithmic number of vertices.模板:Sfnp
- According to a result of Moon & Moser (1965), a graph with 3n vertices can have at most 3n maximal cliques. The graphs meeting this bound are the Moon–Moser graphs K3,3,..., a special case of the Turán graphs arising as the extremal cases in Turán's theorem.
- Hadwiger's conjecture, still unproven, relates the size of the largest clique minor in a graph (its Hadwiger number) to its chromatic number.
- The Erdős–Faber–Lovász conjecture is another unproven statement relating graph coloring to cliques.
- 托兰定理在 稠密图Dense graph中给出了团大小的下界。如果一个图具有足够多的边,则它必然含有较大的团。例如,每个具有n个顶点且超过个边的图形都必然含一个三顶点团。
- 拉姆齐Ramsey's theorem定理指出,每个图或其补图都包含至少一个具有对数个顶点的团。
- 根据Moon&Moser(1965)的研究结果,一个具有3n个顶点的图最多可以有3n个极大团。满足此极限要求的图被称为Moon&Moser图K3,3,...,该图相当于托兰图的特例,是托兰定理中的极端情况。
- 关于Hadwiger的猜想,目前尚未得到证实,其认为图中最大的团子式的大小(即Hadwiger数)与其色数相关。
- Erdős–Faber–Lovász猜想是另一个未经证实的陈述,同样认为图的着色与团相关。
Several important classes of graphs may be defined or characterized by their cliques: Several important classes of graphs may be defined or characterized by their cliques: 由"团"的特性来定义和区分"图"类别的相关描述:
- A cluster graph is a graph whose connected components are cliques.
- A block graph is a graph whose biconnected components are cliques.
- A chordal graph is a graph whose vertices can be ordered into a perfect elimination ordering, an ordering such that the neighbors of each vertex v that come later than v in the ordering form a clique.
- A cograph is a graph all of whose induced subgraphs have the property that any maximal clique intersects any maximal independent set in a single vertex.
- An interval graph is a graph whose maximal cliques can be ordered in such a way that, for each vertex v, the cliques containing v are consecutive in the ordering.
- A line graph is a graph whose edges can be covered by edge-disjoint cliques in such a way that each vertex belongs to exactly two of the cliques in the cover.
- A perfect graph is a graph in which the clique number equals the chromatic number in every induced subgraph.
- A split graph is a graph in which some clique contains at least one endpoint of every edge.
- A triangle-free graph is a graph that has no cliques other than its vertices and edges.
- 聚类图Cluster graph是图的一种特例,其连接的组成部分视为团。
- 框图Block graph是图的一种特例,其双连通的部分视为团。
- 弦图Chordal graph是图的一种特例,其顶点可以按照最佳删除顺序进行排序;也就是说每个顶点的相邻点(即与其构成一个团的另一个顶点)为该顶点的后续点。
- 余图Cograph是图的一种特例,其所有的导出子图均具有以下特性:任何极大团与任何极大独立集都相交于一个独立点。
- 区间图Interval graph是图的一种特例,其极大团按照一定顺序排列,对于每个顶点v,所有包含其顶点v的团均连续排列。
- 线图Line graph是图的一种特例,其连边可以被不相交的边团覆盖,从而使得每个顶点恰好属于该覆盖区域中的两个团。
- 完美图Perfect graph是图的一种特例,其导出子图的色数等于此导出子图的团数。
- 分裂图Split graph是图的一种特例,其中存在某个团包含至少一个顶点,该顶点为每条边的端点。
- 三角形无关图Triangle-free graph是图的一种特例,除了顶点和连边之外,该图不含任何团。
Additionally, many other mathematical constructions involve cliques in graphs. Among them, Additionally, many other mathematical constructions involve cliques in graphs. Among them, 此外,还有许多其他数学结构与图论的"团"有关。它们包括,
- The clique complex of a graph G is an abstract simplicial complex X(G) with a simplex for every clique in G
- A simplex graph is an undirected graph κ(G) with a vertex for every clique in a graph G and an edge connecting two cliques that differ by a single vertex. It is an example of median graph, and is associated with a median algebra on the cliques of a graph: the median m(A,B,C) of three cliques A, B, and C is the clique whose vertices belong to at least two of the cliques A, B, and C.[2]
- The clique-sum is a method for combining two graphs by merging them along a shared clique.
- Clique-width is a notion of the complexity of a graph in terms of the minimum number of distinct vertex labels needed to build up the graph from disjoint unions, relabeling operations, and operations that connect all pairs of vertices with given labels. The graphs with clique-width one are exactly the disjoint unions of cliques.
- The intersection number of a graph is the minimum number of cliques needed to cover all the graph's edges.
- The clique graph of a graph is the intersection graph of its maximal cliques.
- 图G的 团复形Clique complex属于 抽象复形Abstract simplicial complex,其中图G的每个团都为单纯形。
- 单纯形图Simplex graph可记为无向图κ(G),它具有图G中每个团的一个顶点,以及一个连边,并且该连边通过一个顶点将两个不同的团相连。
- 团相加Clique-sum指的是将两个图合并,沿着他们共有团的顶点和连边融合形成。
- 团宽度Clique-width是图复杂性的一个概念,是用来说明图结构复杂性的一个参数。该图由最少数量的不同定点标签组成,并通过以下操作建立:
- 将两个已标记的图拆开,使其不相交;
- 重新标记;
- 根据给定的标记,连接所有成对顶点。
- 图的 交叉数Intersection number指的是能覆盖图所有连边所需的最小团数。
- 图G的 团图Clique graph指的是该图的极大团的交叉图Intersection graph。主要为了展示图G的团结构。
Closely related concepts to complete subgraphs are subdivisions of complete graphs and complete graph minors. In particular, Kuratowski's theorem and Wagner's theorem characterize planar graphs by forbidden complete and complete bipartite subdivisions and minors, respectively.
Closely related concepts to complete subgraphs are subdivisions of complete graphs and complete graph minors. In particular, Kuratowski's theorem and Wagner's theorem characterize planar graphs by forbidden complete and complete bipartite subdivisions and minors, respectively.
从概念上来说,完全子图与完全图细分,以及完全图子式密切相关。尤其是Kuratowski定理和Wagner定理,它们就是通过禁用完全图、完全二分图细分和完全二分图子式来描述平面图特征的。
Computer science 计算机科学
In computer science, the clique problem is the computational problem of finding a maximum clique, or all cliques, in a given graph. It is NP-complete, one of Karp's 21 NP-complete problems.模板:Sfnp It is also fixed-parameter intractable, and hard to approximate. Nevertheless, many algorithms for computing cliques have been developed, either running in exponential time (such as the Bron–Kerbosch algorithm) or specialized to graph families such as planar graphs or perfect graphs for which the problem can be solved in polynomial time.
In computer science, the clique problem is the computational problem of finding a maximum clique, or all cliques, in a given graph. It is NP-complete, one of Karp's 21 NP-complete problems. It is also fixed-parameter intractable, and hard to approximate. Nevertheless, many algorithms for computing cliques have been developed, either running in exponential time (such as the Bron–Kerbosch algorithm) or specialized to graph families such as planar graphs or perfect graphs for which the problem can be solved in polynomial time.
在计算机科学中,团问题指的是在给定图中查找最大团或所有团的计算问题。它是是Karp的21个NP完全问题之一。它也是固定参数难求解问题,甚至难以获得近似值。尽管如此,目前专业人士已经开发了诸多用于计算团的算法,包括可以在指数时间内求解的例如Bron–Kerbosch的算法,以及专门用于求解图族(例如平面图或完美图)这类问题的算法,并在多项式时间内解决。
Applications 应用
The word "clique", in its graph-theoretic usage, arose from the work of Luce & Perry (1949), who used complete subgraphs to model cliques (groups of people who all know each other) in social networks. The same definition was used by Festinger (1949) in an article using less technical terms. Both works deal with uncovering cliques in a social network using matrices. For continued efforts to model social cliques graph-theoretically, see e.g. Alba (1973), Peay (1974), and Doreian & Woodard (1994).
The word "clique", in its graph-theoretic usage, arose from the work of , who used complete subgraphs to model cliques (groups of people who all know each other) in social networks. The same definition was used by in an article using less technical terms. Both works deal with uncovering cliques in a social network using matrices. For continued efforts to model social cliques graph-theoretically, see e.g. , , and .
“团clique”一词在图形理论上的使用,来源于Luce&Perry(1949)的研究《A method of matrix analysis of group structure》,他们通过完全子图对社交网络中的集团(彼此认识的人群)进行建模。之后Festinger(1949)在较少术语的文章《The analysis of sociograms using matrix algebra》中使用了相同的定义。这两部作品都通过使用矩阵的方法来在社交网络中处理团发现问题。之后,Alba(1973),Peay(1974)和Doreian&Woodard(1994)以图理论为基础对社交团体继续进行了图形化建模。
Many different problems from bioinformatics have been modeled using cliques. For instance, Ben-Dor, Shamir & Yakhini (1999) model the problem of clustering gene expression data as one of finding the minimum number of changes needed to transform a graph describing the data into a graph formed as the disjoint union of cliques; Tanay, Sharan & Shamir (2002) discuss a similar biclustering problem for expression data in which the clusters are required to be cliques. Sugihara (1984) uses cliques to model ecological niches in food webs. Day & Sankoff (1986) describe the problem of inferring evolutionary trees as one of finding maximum cliques in a graph that has as its vertices characteristics of the species, where two vertices share an edge if there exists a perfect phylogeny combining those two characters. Samudrala & Moult (1998) model protein structure prediction as a problem of finding cliques in a graph whose vertices represent positions of subunits of the protein. And by searching for cliques in a protein-protein interaction network, Spirin & Mirny (2003) found clusters of proteins that interact closely with each other and have few interactions with proteins outside the cluster. Power graph analysis is a method for simplifying complex biological networks by finding cliques and related structures in these networks.
Many different problems from bioinformatics have been modeled using cliques. For instance, model the problem of clustering gene expression data as one of finding the minimum number of changes needed to transform a graph describing the data into a graph formed as the disjoint union of cliques; discuss a similar biclustering problem for expression data in which the clusters are required to be cliques. uses cliques to model ecological niches in food webs. describe the problem of inferring evolutionary trees as one of finding maximum cliques in a graph that has as its vertices characteristics of the species, where two vertices share an edge if there exists a perfect phylogeny combining those two characters. model protein structure prediction as a problem of finding cliques in a graph whose vertices represent positions of subunits of the protein. And by searching for cliques in a protein-protein interaction network, found clusters of proteins that interact closely with each other and have few interactions with proteins outside the cluster. Power graph analysis is a method for simplifying complex biological networks by finding cliques and related structures in these networks.
在生物信息学领域,诸多不同问题都已经通过“团”来实现建模。例如,Ben-Dor,Shamir和Yakhini(1999)对基因表达数据的聚类问题进行了建模,通过将数据描述的图转换为含有不相交团的图,并在转变过程中找寻最小改变量。另外,Tanay,Sharan&Shamir(2002)讨论了一个类似的表达数据的双聚类问题,在该问题中,群集被描述为“团”。Sugihara(1984)使用“团”对食物网中的生态位进行建模。Day&Sankoff(1986)将推论进化树的问题描述为在具有该物种顶点特征的图形中找到最大团的问题之一,如果存在一个可能能将这两个特征完美结合,则两个顶点共享一条边。Samudrala&Moult(1998)将蛋白质结构预测模型化为在图中顶点表示蛋白质亚基位置的图中发现团簇的问题。通过在蛋白质-蛋白质相互作用网络中寻找群体,Spirin&Mirny(2003)发现了彼此紧密相互作用的蛋白质簇,并且与簇外部的蛋白质几乎没有相互作用。功率图分析是一种通过在这些网络中查找团簇和相关结构来简化复杂生物网络的方法。
In electrical engineering, Prihar (1956) uses cliques to analyze communications networks, and Paull & Unger (1959) use them to design efficient circuits for computing partially specified Boolean functions. Cliques have also been used in automatic test pattern generation: a large clique in an incompatibility graph of possible faults provides a lower bound on the size of a test set.[3] Cong & Smith (1993) describe an application of cliques in finding a hierarchical partition of an electronic circuit into smaller subunits.
In electrical engineering, uses cliques to analyze communications networks, and use them to design efficient circuits for computing partially specified Boolean functions. Cliques have also been used in automatic test pattern generation: a large clique in an incompatibility graph of possible faults provides a lower bound on the size of a test set. describe an application of cliques in finding a hierarchical partition of an electronic circuit into smaller subunits.
在电气工程中,Prihar(1956)使用团来分析通信网络,Paull&Unger(1959)使用它们来设计有效的电路,以计算部分指定的布尔函数。团也已用于自动测试模式生成:不兼容图中可能出现的故障的大团为测试集的大小提供了下限。Cong&Smith(1993)描述了团在寻找将电子电路分层划分成较小的子单元中的应用。
In chemistry, Rhodes et al. (2003) use cliques to describe chemicals in a chemical database that have a high degree of similarity with a target structure. Kuhl, Crippen & Friesen (1983) use cliques to model the positions in which two chemicals will bind to each other.
In chemistry, use cliques to describe chemicals in a chemical database that have a high degree of similarity with a target structure. use cliques to model the positions in which two chemicals will bind to each other.
在化学上,Rhodes等学者(2003年)使用团来描述化学数据库中与目标结构具有高度相似性的化学物质。Kuhl,Crippen&Friesen(1983)使用团对两种化学物质相互结合的位置进行建模。
See also 其他参考资料
Notes 备注
- ↑ The earlier work by Kuratowski (1930) characterizing planar graphs by forbidden complete and complete bipartite subgraphs was originally phrased in topological rather than graph-theoretic terms.
- ↑ Barthélemy, Leclerc & Monjardet (1986), page 200.
- ↑ Hamzaoglu & Patel (1998).
References 参考文献
- Alba, Richard D. (1973), "A graph-theoretic definition of a sociometric clique" (PDF), Journal of Mathematical Sociology, 3 (1): 113–126, doi:10.1080/0022250X.1973.9989826.
- Barthélemy, J.-P.; Leclerc, B.; Monjardet, B. (1986), "On the use of ordered sets in problems of comparison and consensus of classifications", Journal of Classification, 3 (2): 187–224, doi:10.1007/BF01894188.
- Ben-Dor, Amir; Shamir, Ron; Yakhini, Zohar (1999), "Clustering gene expression patterns.", Journal of Computational Biology, 6 (3–4): 281–297, CiteSeerX 10.1.1.34.5341, doi:10.1089/106652799318274, PMID 10582567.
- Chang, Maw-Shang; Kloks, Ton; Lee, Chuan-Min (2001), "Maximum clique transversals", 计算机科学中的图论概念(Boltenhagen,2001), Lecture Notes in Comput. Sci., vol. 2204
2204, Springer,Berlin, pp. 32–43, doi:10.1007/3-540-45477-2 _ 5, ISBN 978-3-540-42707-0, MR [//www.ams.org/mathscinet-getitem?mr=1905299%0A%0A1905299%E5%85%88%E7%94%9F 1905299
1905299先生] {{citation}}: Check |doi= value (help); Check |mr= value (help); Unknown parameter |系列= ignored (help); Unknown parameter |贡献= ignored (help); Unknown parameter |页数= ignored (help); line feed character in |mr= at position 8 (help); line feed character in |volume= at position 5 (help).
}}.
}}.
- Cong, J.; Smith, M. (1993), "A parallel bottom-up clustering algorithm with applications to circuit partitioning in VLSI design", Proc. 30th International Design Automation Conference, pp. 755–760, CiteSeerX 10.1.1.32.735, doi:10.1145/157485.165119, ISBN 978-0897915779.
- Day, William H. E.; Sankoff, David (1986), "Computational complexity of inferring phylogenies by compatibility", Systematic Zoology, 35 (2): 224–229, doi:10.2307/2413432, JSTOR 2413432.
- Doreian, Patrick; Woodard, Katherine L. (1994), "Defining and locating cores and boundaries of social networks", Social Networks, 16 (4): 267–293, doi:10.1016/0378-8733(94)90013-2.
- Erdős, Paul; Szekeres, George (1935), "A combinatorial problem in geometry" (PDF), Compositio Mathematica, 2: 463–470.
- Festinger, Leon (1949), "The analysis of sociograms using matrix algebra", Human Relations, 2 (2): 153–158, doi:10.1177/001872674900200205.
- Graham 1 = Graham, R. 1 = r.; Rothschild, B.
2 = b.; Spencer 3 = Spencer, J. H. 3 = j. h. (1990
1990年), [https://archive.org/details/ramseytheory0000grah
Https://archive.org/details/ramseytheory0000grah Ramsey Theory 拉姆齐理论], New York: John Wiley and Sons
约翰威利父子出版社, ISBN 978-0-471-50046-9 {{citation}}: Check |url= value (help); Check date values in: |year= (help); Text "地点: 纽约" ignored (help); line feed character in |first1= at position 3 (help); line feed character in |first2= at position 3 (help); line feed character in |first3= at position 6 (help); line feed character in |last1= at position 7 (help); line feed character in |last3= at position 8 (help); line feed character in |publisher= at position 20 (help); line feed character in |title= at position 14 (help); line feed character in |url= at position 49 (help); line feed character in |year= at position 5 (help).
}}.
}}.
- Hamzaoglu, I.; Patel, J. H. (1998), "Test set compaction algorithms for combinational circuits", Proc. 1998 IEEE/ACM International Conference on Computer-Aided Design, pp. 283–289, doi:10.1145/288548.288615, ISBN 978-1581130089.
- Karp, Richard M. (1972), "Reducibility among combinatorial problems", in Miller, R. E.; Thatcher, J. W. (eds.), Complexity of Computer Computations (PDF), New York: Plenum, pp. 85–103.
- Kuhl, F. S.; Crippen, G. M.; Friesen, D. K. (1983), "A combinatorial algorithm for calculating ligand binding", Journal of Computational Chemistry, 5 (1): 24–34, doi:10.1002/jcc.540050105.
- Kuratowski, Kazimierz (1930), "Sur le problème des courbes gauches en Topologie" (PDF), Fundamenta Mathematicae (in French), 15: 271–283, doi:10.4064/fm-15-1-271-283
{{citation}}: CS1 maint: unrecognized language (link).
- Luce, r. Duncan; Perry, Albert d. (1949), "群结构的矩阵分析方法", Psychometrika, 14 (2): 95–116, doi:10.1007/BF02289146, PMID 18152948.
| pmid = 18152948}}.
18152948}.
- Moon, j. w.; Moser, l. (1965
1965年), "关于图中的团", Israel J. Math. 以色列 j。数学。, 3
3: 23–28
23-28页, doi:10.1007/BF02760024, MR [//www.ams.org/mathscinet-getitem?mr=0182577%20%0A%0A0182577%E5%85%88%E7%94%9F 0182577
0182577先生] {{citation}}: Check |mr= value (help); Check date values in: |year= (help); line feed character in |journal= at position 16 (help); line feed character in |mr= at position 9 (help); line feed character in |pages= at position 6 (help); line feed character in |volume= at position 2 (help); line feed character in |year= at position 5 (help).
| doi = 10.1007/BF02760024}}.
10.1007/BF02760024}.
- Paull, M. C.; Unger, S. H. (1959), "Minimizing the number of states in incompletely specified sequential switching functions", IRE Transactions on Electronic Computers, EC-8 (3): 356–367, doi:10.1109/TEC.1959.5222697.
- Peay, Edmund R. (1974), "Hierarchical clique structures", Sociometry, 37 (1): 54–65, doi:10.2307/2786466, JSTOR 2786466.
- Prihar, Z. (1956), "Topological properties of telecommunications networks", Proceedings of the IRE, 44 (7): 927–933, doi:10.1109/JRPROC.1956.275149.
- Rhodes, Nicholas; Willett, Peter; Calvet, Alain; Dunbar, James B.; Humblet, Christine (2003), "CLIP: similarity searching of 3D databases using clique detection", Journal of Chemical Information and Computer Sciences, 43 (2): 443–448, doi:10.1021/ci025605o, PMID 12653507.
- Samudrala, Ram; Moult, John (1998), "A graph-theoretic algorithm for comparative modeling of protein structure", Journal of Molecular Biology, 279 (1): 287–302, CiteSeerX 10.1.1.64.8918, doi:10.1006/jmbi.1998.1689, PMID 9636717.
- Spirin, Victor; Mirny, Leonid A. (2003), "Protein complexes and functional modules in molecular networks", Proceedings of the National Academy of Sciences, 100 (21): 12123–12128, doi:10.1073/pnas.2032324100, PMC 218723, PMID 14517352.
- Sugihara, George (1984), "Graph theory, homology and food webs", in Levin, Simon A. (ed.), Population Biology, Proc. Symp. Appl. Math., vol. 30, pp. 83–101.
- Tanay, Amos; Sharan, Roded; Shamir, Ron (2002), "Discovering statistically significant biclusters in gene expression data", Bioinformatics, 18 (Suppl. 1): S136–S144, doi:10.1093/bioinformatics/18.suppl_1.S136, PMID 12169541.
- Turán, Paul (1941
1941年), "关于图论中的一个极值问题", Matematikai és Fizikai Lapok (in 匈牙利语), 48
48: 436–452 {{citation}}: Check date values in: |year= (help); Unknown parameter |页数= ignored (help); line feed character in |volume= at position 3 (help); line feed character in |year= at position 5 (help)CS1 maint: unrecognized language (link)
}}
}}
External links 相关链接
Category:Graph theory objects
范畴: 图论对象
This page was moved from wikipedia:en:Clique (graph theory). Its edit history can be viewed at 团(图论)/edithistory
- 调用重复模板参数的页面
- Articles with hatnote templates targeting a nonexistent page
- CS1 errors: unsupported parameter
- CS1 errors: invisible characters
- CS1 errors: MR
- CS1 errors: DOI
- CS1: long volume value
- CS1 errors: unrecognized parameter
- CS1 errors: dates
- CS1 errors: URL
- CS1 maint: unrecognized language
- Graph theory objects
- 待整理页面