KS检验

此词条暂由彩云小译翻译，未经人工整理和审校，带来阅读不便，请见谅。

Illustration of the Kolmogorov–Smirnov statistic. Red line is CDF, blue line is an ECDF, and the black arrow is the K–S statistic.

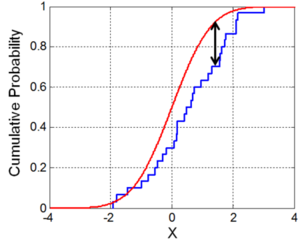
CDF, blue line is an ECDF, and the black arrow is the K–S statistic.]]

蓝线代表 ECDF，黑色箭头代表 k-s 统计。]

In statistics, the Kolmogorov–Smirnov test (K–S test or KS test) is a nonparametric test of the equality of continuous (or discontinuous, see Section 2.2), one-dimensional probability distributions that can be used to compare a sample with a reference probability distribution (one-sample K–S test), or to compare two samples (two-sample K–S test). It is named after Andrey Kolmogorov and Nikolai Smirnov.

In statistics, the Kolmogorov–Smirnov test (K–S test or KS test) is a nonparametric test of the equality of continuous (or discontinuous, see Section 2.2), one-dimensional probability distributions that can be used to compare a sample with a reference probability distribution (one-sample K–S test), or to compare two samples (two-sample K–S test). It is named after Andrey Kolmogorov and Nikolai Smirnov.

在统计学中，Kolmogorov-Smirnov 检验(k-s 检验或 KS 检验)是连续(或不连续，见第2.2节)等式的非参数检验，一维概率分布可用于比较样本与参考概率分布(单样本 k-s 检验) ，或比较两个样本(双样本 k-s 检验)。它以安德雷·柯尔莫哥洛夫和尼古拉斯 · 斯米尔诺夫命名。

The Kolmogorov–Smirnov statistic quantifies a distance between the empirical distribution function of the sample and the cumulative distribution function of the reference distribution, or between the empirical distribution functions of two samples. The null distribution of this statistic is calculated under the null hypothesis that the sample is drawn from the reference distribution (in the one-sample case) or that the samples are drawn from the same distribution (in the two-sample case). In the one-sample case, the distribution considered under the null hypothesis may be continuous (see Section 2), purely discrete or mixed (see Section 2.2). In the two-sample case (see Section 3), the distribution considered under the null hypothesis is a continuous distribution but is otherwise unrestricted.

The Kolmogorov–Smirnov statistic quantifies a distance between the empirical distribution function of the sample and the cumulative distribution function of the reference distribution, or between the empirical distribution functions of two samples. The null distribution of this statistic is calculated under the null hypothesis that the sample is drawn from the reference distribution (in the one-sample case) or that the samples are drawn from the same distribution (in the two-sample case). In the one-sample case, the distribution considered under the null hypothesis may be continuous (see Section 2), purely discrete or mixed (see Section 2.2). In the two-sample case (see Section 3), the distribution considered under the null hypothesis is a continuous distribution but is otherwise unrestricted.

Kolmogorov-Smirnov 统计量化了样本的经验分布函数和参考分布的累积分布函数之间的距离，或者样本的经验分布函数之间的距离。该统计量的零分布是在下述零假设下计算的: 样本是从参考分布中抽取的(在单样本情况下) ，或者样本是从同一分布中抽取的(在双样本情况下)。在单样本情况下，在无效假设下考虑的分布可以是连续的(见第2节) ，纯离散的或混合的(见第2.2节)。在两个样本的情况下(见第3节) ，在零假设下考虑的分布是一个连续的分布，但在其他方面是不受限制的。

The two-sample K–S test is one of the most useful and general nonparametric methods for comparing two samples, as it is sensitive to differences in both location and shape of the empirical cumulative distribution functions of the two samples.

The two-sample K–S test is one of the most useful and general nonparametric methods for comparing two samples, as it is sensitive to differences in both location and shape of the empirical cumulative distribution functions of the two samples.

双样本 k-s 检验是比较两个样本最常用的非参数方法之一，因为它对两个样本的经验累积分布函数的位置和形状的差异都很敏感。

The Kolmogorov–Smirnov test can be modified to serve as a goodness of fit test. In the special case of testing for normality of the distribution, samples are standardized and compared with a standard normal distribution. This is equivalent to setting the mean and variance of the reference distribution equal to the sample estimates, and it is known that using these to define the specific reference distribution changes the null distribution of the test statistic (see Test with estimated parameters). Various studies have found that, even in this corrected form, the test is less powerful for testing normality than the Shapiro–Wilk test or Anderson–Darling test. However, these other tests have their own disadvantages. For instance the Shapiro–Wilk test is known not to work well in samples with many identical values.

F_n(x)={1 \over n}\sum_{i=1}^n I_{[-\infty,x]}(X_i)

F _ n (x) = {1 over n } sum _ { i = 1} ^ n i _ {[-infty，x ]}(x _ i)

Kolmogorov–Smirnov statistic

where I_{[-\infty,x]}(X_i) is the indicator function, equal to 1 if X_i \le x and equal to 0 otherwise.

其中 i _ {[-infty，x ]}(x _ i)是指示函数，如果 x _ i le x 等于1，否则等于0。

The empirical distribution function F_n for n independent and identically distributed (i.i.d.) ordered observations X_i is defined as

The Kolmogorov–Smirnov statistic for a given cumulative distribution function F(x) is

给定累积分布函数 f (x)的 Kolmogorov-Smirnov 统计量是

[math]\displaystyle{ F_n(x)={1 \over n}\sum_{i=1}^n I_{[-\infty,x]}(X_i) }[/math]

D_n= \sup_x |F_n(x)-F(x)|

D _ n = sup _ x | f _ n (x)-f (x) |

where [math]\displaystyle{ I_{[-\infty,x]}(X_i) }[/math] is the indicator function, equal to 1 if [math]\displaystyle{ X_i \le x }[/math] and equal to 0 otherwise.

where supx is the supremum of the set of distances. By the Glivenko–Cantelli theorem, if the sample comes from distribution F(x), then Dn converges to 0 almost surely in the limit when n goes to infinity. Kolmogorov strengthened this result, by effectively providing the rate of this convergence (see Kolmogorov distribution). Donsker's theorem provides a yet stronger result.

其中 supx 是距离集的上确界。根据 Glivenko-Cantelli 定理，如果样本来自分布 f (x) ，那么当 n 趋于无穷大时，Dn 几乎肯定收敛于0。科尔莫戈罗夫通过有效地提供这种收敛速度(见科尔莫戈罗夫分布)强化了这一结果。唐斯克定理提供了一个更强有力的结果。

The Kolmogorov–Smirnov statistic for a given cumulative distribution function F(x) is

In practice, the statistic requires a relatively large number of data points (in comparison to other goodness of fit criteria such as the Anderson–Darling test statistic) to properly reject the null hypothesis.

在实践中，统计需要相对大量的数据点(与其他拟合优度标准相比，如安德森-达林检验统计)才能正确地拒绝零假设。

[math]\displaystyle{ D_n= \sup_x |F_n(x)-F(x)| }[/math]

where sup_x is the supremum of the set of distances. By the Glivenko–Cantelli theorem, if the sample comes from distribution F(x), then D_n converges to 0 almost surely in the limit when [math]\displaystyle{ n }[/math] goes to infinity. Kolmogorov strengthened this result, by effectively providing the rate of this convergence (see Kolmogorov distribution). Donsker's theorem provides a yet stronger result.

The Kolmogorov distribution is the distribution of the random variable

柯尔莫哥洛夫分布是随机变量的分布

In practice, the statistic requires a relatively large number of data points (in comparison to other goodness of fit criteria such as the Anderson–Darling test statistic) to properly reject the null hypothesis.

K=\sup_{t\in[0,1]}|B(t)|

K = sup _ { t in [0,1]} | b (t) |

Kolmogorov distribution

where B(t) is the Brownian bridge. The cumulative distribution function of K is given by

其中 b (t)是布朗桥。的累积分布函数是由

The Kolmogorov distribution is the distribution of the random variable

\operatorname{Pr}(K\leq x)=1-2\sum_{k=1}^\infty (-1)^{k-1} e^{-2k^2 x^2}=\frac{\sqrt{2\pi}}{x}\sum_{k=1}^\infty e^{-(2k-1)^2\pi^2/(8x^2)},

操作名{ Pr }(k leq x) = 1-2 sum { k = 1} ^ infty (- 1) ^ { k-1} e ^ {-2 k ^ 2 x ^ 2} = frac { sqrt {2 pi }{ x } sum { k = 1} ^ infty e ^ {-(2k-1) ^ 2 pi ^ 2/(8x ^ 2)} ,

[math]\displaystyle{ K=\sup_{t\in[0,1]}|B(t)| }[/math]

which can also be expressed by the Jacobi theta function \vartheta_{01}(z=0;\tau=2ix^2/\pi). Both the form of the Kolmogorov–Smirnov test statistic and its asymptotic distribution under the null hypothesis were published by Andrey Kolmogorov, while a table of the distribution was published by Nikolai Smirnov. Recurrence relations for the distribution of the test statistic in finite samples are available.

也可以用 Jacobi theta 函数 vartheta _ {01}(z = 0; tau = 2ix ^ 2/pi)来表示。安德雷·柯尔莫哥洛夫发表了 Kolmogorov-Smirnov 检验统计量的形式及其在无效假设下的渐近分布，Nikolai Smirnov 发表了分布表。有限样本中检验统计量分布的递推关系是可行的。

where B(t) is the Brownian bridge. The cumulative distribution function of K is given by

The goodness-of-fit test or the Kolmogorov–Smirnov test can be constructed by using the critical values of the Kolmogorov distribution. This test is asymptotically valid when n \to\infty. It rejects the null hypothesis at level \alpha if

利用 Kolmogorov 分布的临界值可以构造拟合优度检验或 Kolmogorov-Smirnov 检验。当 n 为无穷时，这个检验是渐近有效的。它在 alpha 级拒绝无效假设，如果

[math]\displaystyle{ \operatorname{Pr}(K\leq x)=1-2\sum_{k=1}^\infty (-1)^{k-1} e^{-2k^2 x^2}=\frac{\sqrt{2\pi}}{x}\sum_{k=1}^\infty e^{-(2k-1)^2\pi^2/(8x^2)}, }[/math]

\sqrt{n}D_n>K_\alpha,\,

1,2,2,3,

which can also be expressed by the Jacobi theta function [math]\displaystyle{ \vartheta_{01}(z=0;\tau=2ix^2/\pi) }[/math]. Both the form of the Kolmogorov–Smirnov test statistic and its asymptotic distribution under the null hypothesis were published by Andrey Kolmogorov, while a table of the distribution was published by Nikolai Smirnov. Recurrence relations for the distribution of the test statistic in finite samples are available.

where Kα is found from

kα 是从哪里发现的

Under null hypothesis that the sample comes from the hypothesized distribution F(x),

\operatorname{Pr}(K\leq K_\alpha)=1-\alpha.\,

操作者名{ Pr }(k leq k _ alpha) = 1-alpha. ,

[math]\displaystyle{ \sqrt{n}D_n\xrightarrow{n\to\infty}\sup_t |B(F(t))| }[/math]

The asymptotic power of this test is 1.

这个检验的渐近幂是1。

in distribution, where B(t) is the Brownian bridge.

Fast and accurate algorithms to compute the cdf \operatorname{Pr}(D_n \leq x) or its complement for arbitrary n and x, are available from:

计算任意 n 和 x 的 cdf 操作数{ Pr }(d _ n leq x)或其补数的快速而准确的算法可从以下方面获得:

If F is continuous then under the null hypothesis [math]\displaystyle{ \sqrt{n}D_n }[/math] converges to the Kolmogorov distribution, which does not depend on F. This result may also be known as the Kolmogorov theorem. The accuracy of this limit as an approximation to the exact cdf of [math]\displaystyle{ K }[/math] when [math]\displaystyle{ n }[/math] is finite is not very impressive: even when [math]\displaystyle{ n=1000 }[/math], the corresponding maximum error is about [math]\displaystyle{ 0.9\% }[/math]; this error increases to [math]\displaystyle{ 2.6\% }[/math] when [math]\displaystyle{ n=100 }[/math] and to a totally unacceptable [math]\displaystyle{ 7\% }[/math] when [math]\displaystyle{ n=10 }[/math]. However, a very simple expedient of replacing [math]\displaystyle{ x }[/math] by

[math]\displaystyle{ x+\frac{1}{6\sqrt{n}}+ \frac{x-1}{4n} }[/math]

Using estimated parameters, the questions arises which estimation method should be used. Usually this would be the maximum likelihood method, but e.g. for the normal distribution MLE has a large bias error on sigma. Using a moment fit or KS minimization instead has a large impact on the critical values, and also some impact on test power. If we need to decide for Student-T data with df = 2 via KS test whether the data could be normal or not, then a ML estimate based on H0 (data is normal, so using the standard deviation for scale) would give much larger KS distance, than a fit with minimum KS. In this case we should reject H0, which is often the case with MLE, because the sample standard deviation might be very large for T-2 data, but with KS minimization we may get still a too low KS to reject H0. In the Student-T case, a modified KS test with KS estimate instead of MLE, makes the KS test indeed slightly worse. However, in other cases, such a modified KS test leads to slightly better test power.

利用估计的参数，提出了应采用哪种估计方法的问题。通常这是最大似然法。对于正态分布，极大似然估计对西格玛有很大的偏差。使用矩拟合或 KS 最小化对临界值有较大的影响，对测试功率也有一定的影响。如果我们需要通过 KS 检验来决定 df = 2的 Student-T 数据是否正常，那么基于 h 0的 ML 估计(数据是正常的，因此使用标准差作为标度)将给出更大的 KS 距离，而不是用最小的 KS 拟合。在这种情况下，我们应该拒绝 h 0，这通常是与 MLE 的情况，因为样本标准差可能是非常大的 t 2数据，但与 KS 最小化，我们可能仍然得到一个太低的 KS 拒绝 h 0。在学生 t 的情况下，一个修改的 KS 测试与 KS 估计，而不是 MLE，使 KS 测试确实稍差。然而，在其他情况下，这种修改后的 KS 测试会导致稍微更好的测试能力。

in the argument of the Jacobi theta function reduces these errors to

[math]\displaystyle{ 0.003\% }[/math], [math]\displaystyle{ 0.027\% }[/math], and [math]\displaystyle{ 0.27\% }[/math] respectively; such accuracy would be usually considered more than adequate for all practical applications.

The goodness-of-fit test or the Kolmogorov–Smirnov test can be constructed by using the critical values of the Kolmogorov distribution. This test is asymptotically valid when [math]\displaystyle{ n \to\infty }[/math]. It rejects the null hypothesis at level [math]\displaystyle{ \alpha }[/math] if

Under the assumption that F(x) is non-decreasing and right-continuous, with countable (possibly infinite) number of jumps, the KS test statistic can be expressed as:

假设 f (x)是非递减的，且是右连续的，且具有可数个(可能是无限个)跳跃，KS 检验统计量可以表示为:

[math]\displaystyle{ \sqrt{n}D_n\gt K_\alpha,\, }[/math]

D_n= \sup_x |F_n(x)-F(x)| = \sup_{0 \leq t \leq 1} |F_n(F^{-1}(t)) - F(F^{-1}(t))|.

D _ n = sup _ x | f _ n (x)-f (x) | = sup _ {0 leq t leq 1} | f _ n (f ^ {-1}(t))-f (f ^ {-1}(t)) | .

where K_α is found from

From the right-continuity of F(x), it follows that F(F^{-1}(t)) \geq t and F^{-1}(F(x)) \leq x and hence, the distribution of D_{n} depends on the null distribution F(x), i.e., is no longer distribution-free as in the continuous case. Therefore, a fast and accurate method has been developed to compute the exact and asymptotic distribution of D_{n} when F(x) is purely discrete or mixed as part of the dgof package of the R language. Major statistical packages among which SAS PROC NPAR1WAY , Stata ksmirnov implement the KS test under the assumption that F(x) is continuous, which is more conservative if the null distribution is actually not continuous (see

从 f (x)的右连续性出发，得到 f (f ^ {-1}(t)) geq t 和 f ^ {-1}(f (x)) leq x，因此 d _ { n }的分布取决于空分布 f (x) ，也就是说，不再像连续情形那样是无分布的。因此，我们发展了一种快速而精确的方法来计算当 f (x)是完全离散的或作为 r 语言程序包 dgof 的一部分混合时 d _ { n }的精确和渐近分布。其中 SAS PROC NPAR1WAY、 Stata ksmirnov 等主要统计软件包在 f (x)连续的假设下实现了 KS 检验，如果零分布实际上不是连续的(见

[math]\displaystyle{ \operatorname{Pr}(K\leq K_\alpha)=1-\alpha.\, }[/math]

).

).

The asymptotic power of this test is 1.

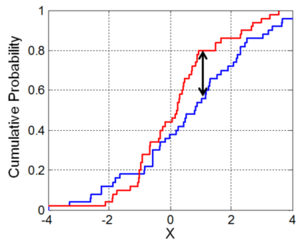
Illustration of the two-sample Kolmogorov–Smirnov statistic. Red and blue lines each correspond to an empirical distribution function, and the black arrow is the two-sample KS statistic.

两样本 Kolmogorov-Smirnov 统计量的图解。红线和蓝线分别对应于一个经验分布函数，黑箭头是两个样本的 KS 统计。

Fast and accurate algorithms to compute the cdf [math]\displaystyle{ \operatorname{Pr}(D_n \leq x) }[/math] or its complement for arbitrary [math]\displaystyle{ n }[/math] and [math]\displaystyle{ x }[/math], are available from:

The Kolmogorov–Smirnov test may also be used to test whether two underlying one-dimensional probability distributions differ. In this case, the Kolmogorov–Smirnov statistic is

Kolmogorov-Smirnov 检验也可用于检验两种潜在的一维概率分布是否不同。在这种情况下，Kolmogorov-Smirnov 统计量是

• and for continuous null distributions with code in C and Java to be found in .

D_{n,m}=\sup_x |F_{1,n}(x)-F_{2,m}(x)|,

D _ { n，m } = sup _ x | f _ {1，n }(x)-f _ {2，m }(x) | ,

• for purely discrete, mixed or continuous null distribution implemented in the KSgeneral package of the R project for statistical computing, which for a given sample also computes the KS test statistic and its p-value. Alternative C++ implementation is available from .

where F_{1,n} and F_{2,m} are the empirical distribution functions of the first and the second sample respectively, and \sup is the supremum function.

其中 f {1，n }和 f {2，m }分别是第一和第二样本的经验分布函数，sup 是上确界函数。

Test with estimated parameters

For large samples, the null hypothesis is rejected at level \alpha if

对于大样本，如果

If either the form or the parameters of F(x) are determined from the data X_i the critical values determined in this way are invalid. In such cases, Monte Carlo or other methods may be required, but tables have been prepared for some cases. Details for the required modifications to the test statistic and for the critical values for the normal distribution and the exponential distribution have been published, and later publications also include the Gumbel distribution. The Lilliefors test represents a special case of this for the normal distribution. The logarithm transformation may help to overcome cases where the Kolmogorov test data does not seem to fit the assumption that it came from the normal distribution.

D_{n,m}>c(\alpha)\sqrt{\frac{n + m}{n\cdot m}}.

D _ { n，m } > c (alpha) sqrt { frac { n + m }{ n cdot m }.

Using estimated parameters, the questions arises which estimation method should be used. Usually this would be the maximum likelihood method, but e.g. for the normal distribution MLE has a large bias error on sigma. Using a moment fit or KS minimization instead has a large impact on the critical values, and also some impact on test power. If we need to decide for Student-T data with df = 2 via KS test whether the data could be normal or not, then a ML estimate based on H₀ (data is normal, so using the standard deviation for scale) would give much larger KS distance, than a fit with minimum KS. In this case we should reject H₀, which is often the case with MLE, because the sample standard deviation might be very large for T-2 data, but with KS minimization we may get still a too low KS to reject H₀. In the Student-T case, a modified KS test with KS estimate instead of MLE, makes the KS test indeed slightly worse. However, in other cases, such a modified KS test leads to slightly better test power.

Where n and m are the sizes of first and second sample respectively. The value of c({\alpha}) is given in the table below for the most common levels of \alpha

其中 n 和 m 分别是第一和第二个样本的尺寸。下表给出了最常见的 alpha 级别的 c ({ alpha })值

Discrete and mixed null distribution

{ | class = “ wikitable” Under the assumption that [math]\displaystyle{ F(x) }[/math] is non-decreasing and right-continuous, with countable (possibly infinite) number of jumps, the KS test statistic can be expressed as:

\alpha	0.20	0.15	0.10	0.05	0.025	0.01	0.005	0.001 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 [math]\displaystyle{ D_n= \sup_x |F_n(x)-F(x)| = \sup_{0 \leq t \leq 1} |F_n(F^{-1}(t)) - F(F^{-1}(t))|. }[/math]
c({\alpha})	1.073	1.138	1.224	1.358	1.48	1.628	1.731	1.949 1.073 | 1.138 | 1.224 | 1.358 | 1.48 | 1.628 | 1.731 | 1.949 From the right-continuity of [math]\displaystyle{ F(x) }[/math], it follows that [math]\displaystyle{ F(F^{-1}(t)) \geq t }[/math] and [math]\displaystyle{ F^{-1}(F(x)) \leq x }[/math] and hence, the distribution of [math]\displaystyle{ D_{n} }[/math] depends on the null distribution [math]\displaystyle{ F(x) }[/math], i.e., is no longer distribution-free as in the continuous case. Therefore, a fast and accurate method has been developed to compute the exact and asymptotic distribution of [math]\displaystyle{ D_{n} }[/math] when [math]\displaystyle{ F(x) }[/math] is purely discrete or mixed , implemented in C++ and in the KSgeneral package of the R language. The functions disc_ks_test(), mixed_ks_test() and cont_ks_test() compute also the KS test statistic and p-values for purely discrete, mixed or continuous null distributions and arbitrary sample sizes. The KS test and its p-values for discrete null distributions and small sample sizes are also computed in as part of the dgof package of the R language. Major statistical packages among which SAS PROC NPAR1WAY , Stata ksmirnov implement the KS test under the assumption that [math]\displaystyle{ F(x) }[/math] is continuous, which is more conservative if the null distribution is actually not continuous (see

|}

).

and in general by

一般来说

Two-sample Kolmogorov–Smirnov test

c\left(\alpha\right)=\sqrt{-\ln\left(\tfrac{\alpha}{2}\right)\cdot \tfrac{1}{2}},

C left (alpha right) = sqrt {-ln left (tfrac { alpha }{2} right) cdot tfrac {1}{2} ,

Illustration of the two-sample Kolmogorov–Smirnov statistic. Red and blue lines each correspond to an empirical distribution function, and the black arrow is the two-sample KS statistic.

so that the condition reads

这样条件就是

The Kolmogorov–Smirnov test may also be used to test whether two underlying one-dimensional probability distributions differ. In this case, the Kolmogorov–Smirnov statistic is

D_{n,m}>\frac{1}{\sqrt{n}}\cdot\sqrt{-\ln\left(\tfrac{\alpha}{2}\right)\cdot \tfrac{1 + \tfrac{n}{m}}{2}}.

1}{ sqrt { n }} cdot sqrt {-ln left (tfrac { alpha }{2} right) cdot tfrac {1 + tfrac { n }{ m }{2}}.

[math]\displaystyle{ D_{n,m}=\sup_x |F_{1,n}(x)-F_{2,m}(x)|, }[/math]

Here, again, the larger the sample sizes, the more sensitive the minimal bound: For a given ratio of sample sizes (e.g. m=n), the minimal bound scales in the size of either of the samples according to its inverse square root.

在这里，样本容量越大，最小界限越敏感: 对于给定的样本容量比例(例如:。M = n) ，根据样本的逆平方根得到样本大小的最小界限尺度。

where [math]\displaystyle{ F_{1,n} }[/math] and [math]\displaystyle{ F_{2,m} }[/math] are the empirical distribution functions of the first and the second sample respectively, and [math]\displaystyle{ \sup }[/math] is the supremum function.

Note that the two-sample test checks whether the two data samples come from the same distribution. This does not specify what that common distribution is (e.g. whether it's normal or not normal). Again, tables of critical values have been published. A shortcoming of the Kolmogorov–Smirnov test is that it is not very powerful because it is devised to be sensitive against all possible types of differences between two distribution functions. and showed evidence that the Cucconi test, originally proposed for simultaneously comparing location and scale, is much more powerful than the Kolmogorov–Smirnov test when comparing two distribution functions.

注意，两个样本测试检查两个数据样本是否来自同一分布。这并没有指定公共分布是什么(例如,。是否正常)。同样，已经发布了临界值表。Kolmogorov-Smirnov 检验的一个缺点是它不是很强大，因为它被设计成对两个分布函数之间所有可能的差异类型都很敏感。证据表明，当比较两个分布函数时，最初为同时比较位置和规模而提出的 Cucconi 检验要比 Kolmogorov-Smirnov 检验强大得多。

For large samples, the null hypothesis is rejected at level [math]\displaystyle{ \alpha }[/math] if

[math]\displaystyle{ D_{n,m}\gt c(\alpha)\sqrt{\frac{n + m}{n\cdot m}}. }[/math]

Where [math]\displaystyle{ n }[/math] and [math]\displaystyle{ m }[/math] are the sizes of first and second sample respectively. The value of [math]\displaystyle{ c({\alpha}) }[/math] is given in the table below for the most common levels of [math]\displaystyle{ \alpha }[/math]

While the Kolmogorov–Smirnov test is usually used to test whether a given F(x) is the underlying probability distribution of Fn(x), the procedure may be inverted to give confidence limits on F(x) itself. If one chooses a critical value of the test statistic Dα such that P(Dn > Dα) = α, then a band of width ±Dα around Fn(x) will entirely contain F(x) with probability 1 − α.

虽然 Kolmogorov-Smirnov 检验通常用来检验给定的 f (x)是否是 Fn (x)的基本概率分布，但是这个过程可以被反转来给出 f (x)本身的置信限。如果选择检验统计量 dα 的一个临界值使 p (Dn > dα) = α，则 Fn (x)周围的一条宽度 ± dα 带将完全包含 f (x) ，概率为1-α。

A distribution-free multivariate Kolmogorov–Smirnov goodness of fit test has been proposed by Justel, Peña and Zamar (1997). The test uses a statistic which is built using Rosenblatt's transformation, and an algorithm is developed to compute it in the bivariate case. An approximate test that can be easily computed in any dimension is also presented. Justel、 Peña 和 Zamar (1997)提出了一种无分布多元 Kolmogorov-Smirnov 拟合优度检验方法。该检验使用了一个基于 Rosenblatt 变换的统计量，并开发了一个二元情况下的统计量计算算法。本文还给出了一个可以方便地计算任意维数的近似试验。 The Kolmogorov–Smirnov test statistic needs to be modified if a similar test is to be applied to multivariate data. This is not straightforward because the maximum difference between two joint cumulative distribution functions is not generally the same as the maximum difference of any of the complementary distribution functions. Thus the maximum difference will differ depending on which of \Pr(x < X \land y < Y) or \Pr(X < x \land Y > y) or any of the other two possible arrangements is used. One might require that the result of the test used should not depend on which choice is made. 如果要对多变量数据应用类似的检验，则需要修改 Kolmogorov-Smirnov 检验统计量。这并不简单，因为两个联合累积分布函数的最大差值通常不等于任何一个互补分布函数的最大差值。因此，最大的差异将取决于 Pr (x < x 土地 y < y)或 Pr (x < x 土地 y > y)或其他两种可能的安排中的任何一种。有人可能会要求所使用的测试的结果不应该取决于作出的选择。

[math]\displaystyle{ \alpha }[/math]	0.20	0.15	0.10	0.05	0.025	0.01	0.005	0.001
[math]\displaystyle{ c({\alpha}) }[/math]	1.073	1.138	1.224	1.358	1.48	1.628	1.731	1.949

One approach to generalizing the Kolmogorov–Smirnov statistic to higher dimensions which meets the above concern is to compare the cdfs of the two samples with all possible orderings, and take the largest of the set of resulting K–S statistics. In d dimensions, there are 2d−1 such orderings. One such variation is due to Peacock

将 Kolmogorov-Smirnov 统计量推广到更高维度的一种方法是将两个样本的 cdfs 与所有可能的排序进行比较，并取得最大的 k-s 统计量集合。在 d 维中，有2d-1这样的排列。一个这样的变化是由于孔雀

(see also Gosset

(参见戈塞特

and in general by

for a 3D version)

3 d 版本)

and another to Fasano and Franceschini (see Lopes et al. for a comparison and computational details). Critical values for the test statistic can be obtained by simulations, but depend on the dependence structure in the joint distribution.

另一个是 Fasano 和 Franceschini (见 Lopes 等人。以便进行比较和计算细节)。通过仿真可以得到检验统计量的临界值，但这个临界值取决于联合分布中的相关结构。

[math]\displaystyle{ c\left(\alpha\right)=\sqrt{-\ln\left(\tfrac{\alpha}{2}\right)\cdot \tfrac{1}{2}}, }[/math]

In one dimension, the Kolmogorov–Smirnov statistic is identical to the so-called star discrepancy D, so another native KS extension to higher dimensions would be simply to use D also for higher dimensions. Unfortunately, the star discrepancy is hard to calculate in high dimensions.

在一个维度上，Kolmogorov-Smirnov 统计量与所谓的恒星差异 d 是一致的，所以另一个本地的 KS 对更高维度的扩展将是简单地对更高维度也使用 d。不幸的是，在高维空间中，恒星的差异很难计算。

so that the condition reads

[math]\displaystyle{ D_{n,m}\gt \frac{1}{\sqrt{n}}\cdot\sqrt{-\ln\left(\tfrac{\alpha}{2}\right)\cdot \tfrac{1 + \tfrac{n}{m}}{2}}. }[/math]

The Kolmogorov-Smirnov test (one or two sampled test verifies the equality of distributions) is implemented in many software programs:

Kolmogorov-Smirnov 检验(一个或两个抽样检验验证分布是否相等)在许多软件程序中实现:

Here, again, the larger the sample sizes, the more sensitive the minimal bound: For a given ratio of sample sizes (e.g. [math]\displaystyle{ m=n }[/math]), the minimal bound scales in the size of either of the samples according to its inverse square root.

Note that the two-sample test checks whether the two data samples come from the same distribution. This does not specify what that common distribution is (e.g. whether it's normal or not normal). Again, tables of critical values have been published. A shortcoming of the Kolmogorov–Smirnov test is that it is not very powerful because it is devised to be sensitive against all possible types of differences between two distribution functions. and showed evidence that the Cucconi test, originally proposed for simultaneously comparing location and scale, is much more powerful than the Kolmogorov–Smirnov test when comparing two distribution functions.

Setting confidence limits for the shape of a distribution function

While the Kolmogorov–Smirnov test is usually used to test whether a given F(x) is the underlying probability distribution of F_n(x), the procedure may be inverted to give confidence limits on F(x) itself. If one chooses a critical value of the test statistic D_α such that P(D_n > D_α) = α, then a band of width ±D_α around F_n(x) will entirely contain F(x) with probability 1 − α.

The Kolmogorov–Smirnov statistic in more than one dimension

A distribution-free multivariate Kolmogorov–Smirnov goodness of fit test has been proposed by Justel, Peña and Zamar (1997). The test uses a statistic which is built using Rosenblatt's transformation, and an algorithm is developed to compute it in the bivariate case. An approximate test that can be easily computed in any dimension is also presented.

The Kolmogorov–Smirnov test statistic needs to be modified if a similar test is to be applied to multivariate data. This is not straightforward because the maximum difference between two joint cumulative distribution functions is not generally the same as the maximum difference of any of the complementary distribution functions. Thus the maximum difference will differ depending on which of [math]\displaystyle{ \Pr(x \lt X \land y \lt Y) }[/math] or [math]\displaystyle{ \Pr(X \lt x \land Y \gt y) }[/math] or any of the other two possible arrangements is used. One might require that the result of the test used should not depend on which choice is made.

One approach to generalizing the Kolmogorov–Smirnov statistic to higher dimensions which meets the above concern is to compare the cdfs of the two samples with all possible orderings, and take the largest of the set of resulting K–S statistics. In d dimensions, there are 2^d−1 such orderings. One such variation is due to Peacock

(see also Gosset

for a 3D version)

 | last = Eadie

| last = Eadie

and another to Fasano and Franceschini (see Lopes et al. for a comparison and computational details). Critical values for the test statistic can be obtained by simulations, but depend on the dependence structure in the joint distribution.

 | first = W.T. |author2=D. Drijard |author3=F.E. James |author4=M. Roos |author5=B. Sadoulet

第一个 = w.t。2 = d.3 = f.e.4 = m.5 = b.女名女子名

 | title = Statistical Methods in Experimental Physics

实验物理中的统计方法

In one dimension, the Kolmogorov–Smirnov statistic is identical to the so-called star discrepancy D, so another native KS extension to higher dimensions would be simply to use D also for higher dimensions. Unfortunately, the star discrepancy is hard to calculate in high dimensions.

 | publisher = North-Holland

| publisher = North-Holland

 | year = 1971

1971年

Implementations

 | location = Amsterdam

地点: 阿姆斯特丹

The Kolmogorov-Smirnov test (one or two sampled test verifies the equality of distributions) is implemented in many software programs:

 | pages = 269–271

| 页数 = 269-271

 | isbn = 978-0-444-10117-4 }}

| isbn = 978-0-444-10117-4}

• Mathematica has KolmogorovSmirnovTest

• MATLAB has kstest in its Statistics Toolbox.

 | last1 = Stuart

1 = Stuart

• The R package "KSgeneral" computes the KS test statistics and its p-values under arbitrary, possibly discrete, mixed or continuous null distribution.

 | first1 = Alan

1 = Alan

• R's statistics base-package implements the test as ks.test {stats} in its "stats" package.

 | first2 = Keith

2 = Keith

• SAS implements the test in its PROC NPAR1WAY procedure.

 | last2 = Ord

2 = Ord

• Python has an implementation of this test provided by SciPy by Statistical functions (scipy.stats)

 | first3=Steven [F.]

| first3 = Steven [ f. ]

• SYSTAT (SPSS Inc., Chicago, IL)

 | last3=Arnold

3 = Arnold

• Java has an implementation of this test provided by Apache Commons

 | title=Classical Inference and the Linear Model

经典推理和线性模型

• KNIME has a node implementing this test based on the above Java implementation

 | edition=Sixth

第六版

• StatsDirect (StatsDirect Ltd, Manchester, UK) implements all common variants.

 | series = Kendall's Advanced Theory of Statistics

系列 = Kendall 的高级统计理论

• Stata (Stata Corporation, College Station, TX) implements the test in ksmirnov (Kolmogorov–Smirnov equality-of-distributions test) command.

 | volume = 2A

2A

• PSPP implements the test in its KOLMOGOROV-SMIRNOV (or using K-S shortcut function.

 | year = 1999

1999年

• Excel runs the test as KSCRIT and KSPROB

 | publisher = Arnold

阿诺德

 | location = London

| 地点: 伦敦

See also

 | isbn=978-0-340-66230-4

| isbn = 978-0-340-66230-4

• Lepage test

 | mr=1687411

1687411先生

• Cucconi test

 | pages = 25.37–25.43 }}

| pages = 25.37-25.43}

• Kuiper's test

• Shapiro–Wilk test

• Anderson–Darling test

• Cramér–von Mises test

Further reading

• Daniel, Wayne W. (1990). "Kolmogorov–Smirnov one-sample test". Applied Nonparametric Statistics (2nd ed.). Boston: PWS-Kent. pp. 319–330. ISBN 978-0-534-91976-4. https://books.google.com/books?id=0hPvAAAAMAAJ&pg=PA319. 

• Eadie, W.T.; D. Drijard; F.E. James; M. Roos; B. Sadoulet (1971). Statistical Methods in Experimental Physics. Amsterdam: North-Holland. pp. 269–271

Category:Statistical tests

类别: 统计测试. ISBN 978-0-444-10117-4. 

Category:Statistical distance

类别: 统计距离

• {{cite book

Category:Nonparametric statistics

类别: 无母数统计

 | last1 = Stuart

Category:Normality tests

分类: 正常性测试

This page was moved from wikipedia:en:Kolmogorov–Smirnov test. Its edit history can be viewed at KS检验/edithistory