“顶点”的版本间的差异
1220978308(讨论 | 贡献) |
1220978308(讨论 | 贡献) |
||
| 第52行: | 第52行: | ||
The degree of a vertex, denoted 𝛿(v) in a graph is the number of edges incident to it. An isolated vertex is a vertex with degree zero; that is, a vertex that is not an endpoint of any edge (the example image illustrates one isolated vertex). A leaf vertex (also pendant vertex) is a vertex with degree one. In a directed graph, one can distinguish the outdegree (number of outgoing edges), denoted 𝛿<sup> +</sup>(v), from the indegree (number of incoming edges), denoted 𝛿<sup>−</sup>(v); a source vertex is a vertex with indegree zero, while a sink vertex is a vertex with outdegree zero. A simplicial vertex is one whose neighbors form a clique: every two neighbors are adjacent. A universal vertex is a vertex that is adjacent to every other vertex in the graph. | The degree of a vertex, denoted 𝛿(v) in a graph is the number of edges incident to it. An isolated vertex is a vertex with degree zero; that is, a vertex that is not an endpoint of any edge (the example image illustrates one isolated vertex). A leaf vertex (also pendant vertex) is a vertex with degree one. In a directed graph, one can distinguish the outdegree (number of outgoing edges), denoted 𝛿<sup> +</sup>(v), from the indegree (number of incoming edges), denoted 𝛿<sup>−</sup>(v); a source vertex is a vertex with indegree zero, while a sink vertex is a vertex with outdegree zero. A simplicial vertex is one whose neighbors form a clique: every two neighbors are adjacent. A universal vertex is a vertex that is adjacent to every other vertex in the graph. | ||
| − | <font color="#32cd32"> | + | <font color="#32cd32">图中顶点的'''</font><font color="#ff8000">度数</font><font color="#32cd32">'''(用𝛿(v)表示)是关联到它的边的数目</font>。一个'''<font color="#ff8000">孤立顶点</font>'''是一个度为零的顶点,也就是说,是一个不是任何边的端点的顶点(示例图片中有一个'''<font color="#ff8000">孤立顶点</font>'''的例子)。'''<font color="#ff8000">叶顶点</font>'''(也称作'''<font color="#ff8000">悬挂点</font>''')是度数为1的顶点。在有向图中,我们可以区分<font color="#32cd32">外度(外出边数)</font>(用 𝛿<sup> +</sup>(v) 表示),和<font color="#32cd32">外度(外入边数) </font>(用𝛿<sup>−</sup>(v)表示) ; <font color="#32cd32">源顶点</font>是外度为零的顶点,而<font color="#32cd32">汇顶点</font>是具有外度为零的顶点。<font color="#32cd32">单纯形顶点</font>是<font color="#32cd32">邻接</font>成团的顶点:每两个<font color="#32cd32">邻接</font>都是相邻的。<font color="#32cd32">通用顶点</font>是在图中与其他所有顶点都相邻的顶点。 |
| 第60行: | 第60行: | ||
A cut vertex is a vertex the removal of which would disconnect the remaining graph; a vertex separator is a collection of vertices the removal of which would disconnect the remaining graph into small pieces. A k-vertex-connected graph is a graph in which removing fewer than k vertices always leaves the remaining graph connected. An independent set is a set of vertices no two of which are adjacent, and a vertex cover is a set of vertices that includes at least one endpoint of each edge in the graph. The vertex space of a graph is a vector space having a set of basis vectors corresponding with the graph's vertices. | A cut vertex is a vertex the removal of which would disconnect the remaining graph; a vertex separator is a collection of vertices the removal of which would disconnect the remaining graph into small pieces. A k-vertex-connected graph is a graph in which removing fewer than k vertices always leaves the remaining graph connected. An independent set is a set of vertices no two of which are adjacent, and a vertex cover is a set of vertices that includes at least one endpoint of each edge in the graph. The vertex space of a graph is a vector space having a set of basis vectors corresponding with the graph's vertices. | ||
| − | + | '''<font color="#ff8000">割点</font>'''是一类顶点,如果去掉它,就会断开剩余图的连接; <font color="32cd32">顶点分隔符</font>是一组顶点的集合,如果去掉这些顶点,就会将剩余图断裂成小片段。一个<font color="32cd32">k- 顶点连通图</font>是指一类去掉少于 k 个顶点后,剩余部分仍然连通的图。一个<font color="32cd32">独立的集合</font>是一组任意二者均不相邻的顶点群。<font color="32cd32">顶点覆盖</font>是一组顶点,它们均包含图中任意边的至少一个端点。图的'''<font color="#ff8000">顶点空间</font>'''是一个向量空间,它的基向量与图的顶点相对应。 | |
| 第68行: | 第68行: | ||
A graph is vertex-transitive if it has symmetries that map any vertex to any other vertex. In the context of graph enumeration and graph isomorphism it is important to distinguish between labeled vertices and unlabeled vertices. A labeled vertex is a vertex that is associated with extra information that enables it to be distinguished from other labeled vertices; two graphs can be considered isomorphic only if the correspondence between their vertices pairs up vertices with equal labels. An unlabeled vertex is one that can be substituted for any other vertex based only on its adjacencies in the graph and not based on any additional information. | A graph is vertex-transitive if it has symmetries that map any vertex to any other vertex. In the context of graph enumeration and graph isomorphism it is important to distinguish between labeled vertices and unlabeled vertices. A labeled vertex is a vertex that is associated with extra information that enables it to be distinguished from other labeled vertices; two graphs can be considered isomorphic only if the correspondence between their vertices pairs up vertices with equal labels. An unlabeled vertex is one that can be substituted for any other vertex based only on its adjacencies in the graph and not based on any additional information. | ||
| − | + | 如果一个图具有将任何顶点映射到任何其他顶点的对称性,则该图是'''<font color="#ff8000">顶点传递</font>'''的。在<font color="32cd32">图计数</font>和'''<font color="#ff8000">图同构</font>'''的情况下,区分'''<font color="#ff8000">标记顶点</font>'''和'''<font color="#ff8000">非标记顶点</font>'''非常重要。'''<font color="#ff8000">标记顶点</font>'''是与能使其区别于其他'''<font color="#ff8000">标记顶点</font>'''的额外信息相关联的顶点; <font color="32cd32">只有当其顶点之间的对应关系与有相同标记的顶点配对时</font>,两个图才可以被认为是同构的。'''<font color="#ff8000">非标记顶点</font>'''是仅基于其在图中的邻接顶点而不基于任何其他信息就能被其他任意顶点替换的一类顶点。 | |
2020年9月28日 (一) 18:46的版本
此词条暂由彩云小译翻译,未经人工整理和审校,带来阅读不便,请见谅。
本词条由鲁鱼陶阴第一次整理,尚不完善,请见谅。
橙
绿
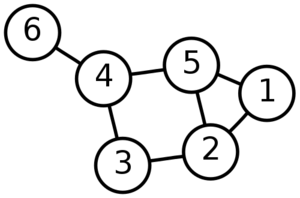
A graph with 6 vertices and 7 edges where the vertex number 6 on the far-left is a leaf vertex or a pendant vertex
一个具有6个 顶点和7条边的图,其中最左边数字6的结点是 叶顶点 Leaf Vertex或叫做 悬挂点 Pendant Vertex
In mathematics, and more specifically in graph theory, a vertex (plural vertices) or node is the fundamental unit of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges (unordered pairs of vertices), while a directed graph consists of a set of vertices and a set of arcs (ordered pairs of vertices). In a diagram of a graph, a vertex is usually represented by a circle with a label, and an edge is represented by a line or arrow extending from one vertex to another.
In mathematics, and more specifically in graph theory, a vertex (plural vertices) or node is the fundamental unit of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges (unordered pairs of vertices), while a directed graph consists of a set of vertices and a set of arcs (ordered pairs of vertices). In a diagram of a graph, a vertex is usually represented by a circle with a label, and an edge is represented by a line or arrow extending from one vertex to another.
在数学上,更具体地说在图论中, 顶点或 节点是形成图的基本单位: 无向图由一组 顶点和一组边(无序 顶点对)组成,而 有向图由一组 顶点和一组弧(有序 顶点对)组成。在图的图解表示中, 顶点通常用带标签的圆来表示,而边则用从一个 顶点延伸到另一个 顶点的直线或箭头来表示。
From the point of view of graph theory, vertices are treated as featureless and indivisible objects, although they may have additional structure depending on the application from which the graph arises; for instance, a semantic network is a graph in which the vertices represent concepts or classes of objects.
From the point of view of graph theory, vertices are treated as featureless and indivisible objects, although they may have additional structure depending on the application from which the graph arises; for instance, a semantic network is a graph in which the vertices represent concepts or classes of objects.
从图论的观点来看, 顶点被视为无特征且不可分割的对象。但是根据图的应用场景, 顶点可能有额外的结构。 例如: 语义网络(计算机科学) ,其中的 顶点表示概念或对象的类。
The two vertices forming an edge are said to be the endpoints of this edge, and the edge is said to be incident to the vertices. A vertex w is said to be adjacent to another vertex v if the graph contains an edge (v,w). The neighborhood of a vertex v is an induced subgraph of the graph, formed by all vertices adjacent to v.
The two vertices forming an edge are said to be the endpoints of this edge, and the edge is said to be incident to the vertices. A vertex w is said to be adjacent to another vertex v if the graph contains an edge (v,w). The neighborhood of a vertex v is an induced subgraph of the graph, formed by all vertices adjacent to v.
形成边的两个 顶点被称为这条边的 端点,这条边称为 关联Incident于这两个 顶点的边。如果图包含一条边(v,w) ,则称一个 顶点w 与另一个 顶点 v 相邻接 Adjacent 。 顶点 v 的邻域(neighborhood)是该图的一个 导出子图(induced subgraph),由邻接于 "v" 的所有 顶点构成。
Types of vertices
Example network with 8 vertices (of which one is isolated) and 10 edges.
用具有8个顶点(其中一个是孤立的)和10条边的网络示意。
The degree of a vertex, denoted 𝛿(v) in a graph is the number of edges incident to it. An isolated vertex is a vertex with degree zero; that is, a vertex that is not an endpoint of any edge (the example image illustrates one isolated vertex).[1] A leaf vertex (also pendant vertex) is a vertex with degree one. In a directed graph, one can distinguish the outdegree (number of outgoing edges), denoted 𝛿 +(v), from the indegree (number of incoming edges), denoted 𝛿−(v); a source vertex is a vertex with indegree zero, while a sink vertex is a vertex with outdegree zero. A simplicial vertex is one whose neighbors form a clique: every two neighbors are adjacent. A universal vertex is a vertex that is adjacent to every other vertex in the graph.
The degree of a vertex, denoted 𝛿(v) in a graph is the number of edges incident to it. An isolated vertex is a vertex with degree zero; that is, a vertex that is not an endpoint of any edge (the example image illustrates one isolated vertex). A leaf vertex (also pendant vertex) is a vertex with degree one. In a directed graph, one can distinguish the outdegree (number of outgoing edges), denoted 𝛿 +(v), from the indegree (number of incoming edges), denoted 𝛿−(v); a source vertex is a vertex with indegree zero, while a sink vertex is a vertex with outdegree zero. A simplicial vertex is one whose neighbors form a clique: every two neighbors are adjacent. A universal vertex is a vertex that is adjacent to every other vertex in the graph.
图中顶点的度数(用𝛿(v)表示)是关联到它的边的数目。一个孤立顶点是一个度为零的顶点,也就是说,是一个不是任何边的端点的顶点(示例图片中有一个孤立顶点的例子)。叶顶点(也称作悬挂点)是度数为1的顶点。在有向图中,我们可以区分外度(外出边数)(用 𝛿 +(v) 表示),和外度(外入边数) (用𝛿−(v)表示) ; 源顶点是外度为零的顶点,而汇顶点是具有外度为零的顶点。单纯形顶点是邻接成团的顶点:每两个邻接都是相邻的。通用顶点是在图中与其他所有顶点都相邻的顶点。
A cut vertex is a vertex the removal of which would disconnect the remaining graph; a vertex separator is a collection of vertices the removal of which would disconnect the remaining graph into small pieces. A k-vertex-connected graph is a graph in which removing fewer than k vertices always leaves the remaining graph connected. An independent set is a set of vertices no two of which are adjacent, and a vertex cover is a set of vertices that includes at least one endpoint of each edge in the graph. The vertex space of a graph is a vector space having a set of basis vectors corresponding with the graph's vertices.
A cut vertex is a vertex the removal of which would disconnect the remaining graph; a vertex separator is a collection of vertices the removal of which would disconnect the remaining graph into small pieces. A k-vertex-connected graph is a graph in which removing fewer than k vertices always leaves the remaining graph connected. An independent set is a set of vertices no two of which are adjacent, and a vertex cover is a set of vertices that includes at least one endpoint of each edge in the graph. The vertex space of a graph is a vector space having a set of basis vectors corresponding with the graph's vertices.
割点是一类顶点,如果去掉它,就会断开剩余图的连接; 顶点分隔符是一组顶点的集合,如果去掉这些顶点,就会将剩余图断裂成小片段。一个k- 顶点连通图是指一类去掉少于 k 个顶点后,剩余部分仍然连通的图。一个独立的集合是一组任意二者均不相邻的顶点群。顶点覆盖是一组顶点,它们均包含图中任意边的至少一个端点。图的顶点空间是一个向量空间,它的基向量与图的顶点相对应。
A graph is vertex-transitive if it has symmetries that map any vertex to any other vertex. In the context of graph enumeration and graph isomorphism it is important to distinguish between labeled vertices and unlabeled vertices. A labeled vertex is a vertex that is associated with extra information that enables it to be distinguished from other labeled vertices; two graphs can be considered isomorphic only if the correspondence between their vertices pairs up vertices with equal labels. An unlabeled vertex is one that can be substituted for any other vertex based only on its adjacencies in the graph and not based on any additional information.
A graph is vertex-transitive if it has symmetries that map any vertex to any other vertex. In the context of graph enumeration and graph isomorphism it is important to distinguish between labeled vertices and unlabeled vertices. A labeled vertex is a vertex that is associated with extra information that enables it to be distinguished from other labeled vertices; two graphs can be considered isomorphic only if the correspondence between their vertices pairs up vertices with equal labels. An unlabeled vertex is one that can be substituted for any other vertex based only on its adjacencies in the graph and not based on any additional information.
如果一个图具有将任何顶点映射到任何其他顶点的对称性,则该图是顶点传递的。在图计数和图同构的情况下,区分标记顶点和非标记顶点非常重要。标记顶点是与能使其区别于其他标记顶点的额外信息相关联的顶点; 只有当其顶点之间的对应关系与有相同标记的顶点配对时,两个图才可以被认为是同构的。非标记顶点是仅基于其在图中的邻接顶点而不基于任何其他信息就能被其他任意顶点替换的一类顶点。
Vertices in graphs are analogous to, but not the same as, vertices of polyhedra: the skeleton of a polyhedron forms a graph, the vertices of which are the vertices of the polyhedron, but polyhedron vertices have additional structure (their geometric location) that is not assumed to be present in graph theory. The vertex figure of a vertex in a polyhedron is analogous to the neighborhood of a vertex in a graph.
Vertices in graphs are analogous to, but not the same as, vertices of polyhedra: the skeleton of a polyhedron forms a graph, the vertices of which are the vertices of the polyhedron, but polyhedron vertices have additional structure (their geometric location) that is not assumed to be present in graph theory. The vertex figure of a vertex in a polyhedron is analogous to the neighborhood of a vertex in a graph.
在图中的顶点类似但不等同于多面体的顶点:多面体的骨架构成一个图,其顶点是多面体的顶点,但多面体的顶点有无法在图论中假定存在的其他结构(几何位置) 。多面体中顶点的顶点图形类似于图中顶点的邻域。
See also
References
- ↑ File:Small Network.png; example image of a network with 8 vertices and 10 edges
- Gallo, Giorgio; Pallotino
2 = Pallotino, Stefano
2 = Stefano (1988
1988年). "Shortest path algorithms
最短路径算法". Annals of Operations Research 运筹学年报. 13
13 (1
1): 1-79 < ! ! ——内联引用引用第4页 -- >. doi:10.1007/BF02288320. {{cite journal}}: Check date values in: |year= (help); line feed character in |first2= at position 8 (help); line feed character in |issue= at position 2 (help); line feed character in |journal= at position 30 (help); line feed character in |last2= at position 10 (help); line feed character in |ref= at position 5 (help); line feed character in |title= at position 25 (help); line feed character in |volume= at position 3 (help); line feed character in |year= at position 5 (help)
}}
}}
- Berge, Claude, Théorie des graphes et ses applications. Collection Universitaire de Mathématiques, II Dunod, Paris 1958, viii+277 pp. (English edition, Wiley 1961; Methuen & Co, New York 1962; Russian, Moscow 1961; Spanish, Mexico 1962; Roumanian, Bucharest 1969; Chinese, Shanghai 1963; Second printing of the 1962 first English edition. Dover, New York 2001)
- Chartrand, Gary (1985). Introductory graph theory. New York: Dover. ISBN 0-486-24775-9. https://archive.org/details/introductorygrap0000char.
- Biggs, Norman; Lloyd, E. H.; Wilson, Robin J. (1986). Graph theory, 1736-1936. Oxford [Oxfordshire]: Clarendon Press. ISBN 0-19-853916-9.
- Harary, Frank (1969). Graph theory. Reading, Mass.: Addison-Wesley Publishing. ISBN 0-201-41033-8.
- Harary, Frank; Palmer, Edgar M. (1973). Graphical enumeration. New York, Academic Press. ISBN 0-12-324245-2.
External links
Category:Graph theory
范畴: 图论
This page was moved from wikipedia:en:Vertex (graph theory). Its edit history can be viewed at 顶点/edithistory