生命围棋

这是一个集智开源项目，力图将John Conway的生命游戏与中国的古老游戏：围棋相结合，开发出一套新的游戏：生命围棋（Go of Life）。

这个游戏的一个测试版本：http://gooflife.com

这里是该项目的GitHub主页：Github

项目背景

简介

生命游戏（Game of Life）是美国数学家John Conway提出来的一款二维的二状态元胞自动机模型。这个模型目前已经成为展示复杂系统涌现现象的典范。该模型用三条异常简单的规则就可以创造出无穷的复杂的行为。其上衍生出来的Pattern已被人们证明是支持通用计算的，也就是说现代计算机可以做的任何运算都可以在生命游戏中得以模拟实现，可以说生命游戏是涌现的封闭计算系统。

围棋是古代中国流传下来的古老棋术之一。它通过黑白两方交替下棋，实现双方的对弈。棋子只能不停地放入棋盘中，当一色棋子被围没有了“气”之后，就会被“提子”。最后，当把所有的棋盘走满，双方通过比较占领的格点数目而评判输赢。围棋这种古老的游戏也是一个利用极其简单的规则，却能涌现出异常复杂的玩法的经典实例，同时也是目前公认人机对弈中最难被AI攻破的棋类，可以说围棋是一种开放式的涌现计算系统。

考虑这两个系统，不难发现它们的共性：1、它们都运行在一个二维的棋盘格子世界上；2、它们的规则都极其简单；3、它们的运行行为或者玩法都充满了复杂性和创造性，都是少即是多设计思想的典范。

深入来讲，首先，它们都有一个棋盘格世界（即二维世界），其次它们都涉及非常有限的格子状态（“生命游戏”中的格子有黑、白两种状态；围棋的格子（确切说是线的交点）有黑、白、空三种状态）；再有，“生命游戏”和围棋的规则都是局部作用的。每一个方格或者棋子都仅仅对它周围的邻居方格或者棋子造成影响。最后，复杂的、长程的相互作用会在这些局部作用中涌现而出。也就是说，涌现性是围棋和“生命游戏”的最大共同点。

因此，我们考虑是否可以制作一款生命围棋游戏，将二者合二为一，结合时下移动互联网的技术和连接红利，进行快速开发和传播。

基本构思

我们的构思是，将生命游戏与围棋在两个不同的尺度上进行融合。具体地，在底层世界，生命游戏按照自己的规则运行；在高层世界，玩家操控棋子玩围棋。

两个层次的交互体现为：高层玩家的棋子实际上是一片固定尺寸的方格世界，按照多数原则分配黑色、白色方格。这些方格可以作为底层生命游戏的初始条件，并按照生命的规则进行演化。反过来，生命游戏的游戏结果会决定高层的围棋游戏行为。也就是说，在高层，玩家的地盘占领除了由围棋规则决定以外，还会受到底层生命游戏规则的影响。生命游戏迫使围棋子进行演化，并可能影响周围的棋盘世界。

这样结合的好处是：1、通过调整参数，我们原则上是可以回退为两个原始的游戏中去。例如，如果一个围棋棋盘格对应于过大的生命游戏方格，那么围棋的游戏规则将几乎不会被生命游戏所影响，因为两个非常大的宏观方格彼此很难相互影响；2、围棋规则经过上千年的演化具有非常高的可玩性，因此将它作为更大的宏观尺度，而生命游戏则自下而上地对围棋进行了微扰，这就会使得围棋规则可能发生一定的变数，有可能会提高可玩性。

数学模型

竞争性的生命游戏

底层按照Conway生命游戏规则，每个格子对应一个或生或死的细胞。

1、细胞周围如果少于2个或大于3个活细胞，下一代则为死细胞

2、死细胞周围如果有3个活细胞，下一代则为活细胞

3、活细胞周围如果2或者3个活细胞，下一代仍为活细胞

我们演绎成一个双人竞争性的生命游戏，即二维方格世界中每个方格会有三种状态：0:空白（死亡），1:黑色（玩家1），2:红色（玩家2）。状态的演化将按照多数原则来实现。

1、竞争性的生命游戏的死亡规则与原始的生命游戏一样。即如果一个黑色或红色细胞周围的黑或红色细胞总数少于2个或者多于3个，那么该细胞会死亡（变成白色）；

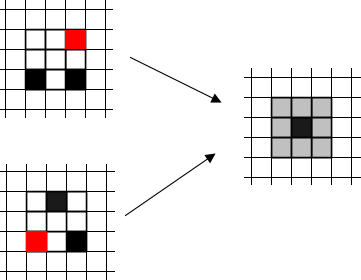
2、由死细胞转为活细胞的时按照多数原则，如图：

其中邻域中黑色比红色细胞多，所以中心的死细胞将变为黑色，否则会变为红色。

3、如果中心是活细胞，周围有2或者3个活细胞也可用类似的多数原则，当出现偶数个相等，即2黑2红情况时，采用继承原则。

围棋

基本规则

1. 对局双方各执一色棋子，黑先白后，交替下子，每次只能下一子。
2. 棋子下在棋盘上的交叉点上。
3. 棋子落子后，不得向其他位置移动。
4. 轮流下子是双方的权利，但允许任何一方放弃下子权。

棋子的气：一个棋子在棋盘上，与它直线紧邻的空点是这个棋子的“气”。棋子直线紧邻的点上，如果有同色棋子存在，则它们便相互连接成一个不可分割的整体。它们的气也应一并计算。棋子直线紧邻的点上，如果有异色棋子存在，这口气就不复存在。如所有的气均为对方所占据，便呈无气状态。无气状态的棋子不能在棋盘上存在，也就是——提子。

提子：把无气之子提出盘外的手段叫“提子”。提子有二种：1.下子后，对方棋子无气，应立即提取。2.下子后，双方棋子都呈无气状态，应立即提取对方无气之子。拔掉对手一颗棋子之后，就是禁着点（也作禁入点）。棋盘上的任何一子，如某方下子后，该子立即呈无气状态，同时又不能提取对方的棋子，这个点，叫做“禁着点”，禁止被提方下子。

在更高的层次，我们将按照围棋的规则运行。

我们知道，围棋是由361个点位构成的。首先，为了让它和生命游戏一致，我们需要将格点转化成方格，这个过程称作【细粒化】，反之而方格转化为格点过程称为【粗粒化】，因为底层生命游戏会生长、扩散、死亡，方格会一个格点可能同时包含两种方格，以统计多数原则决定该格点归属。

这样，361个格点就成为了361个方格。并且棋子就在这些格点中走。

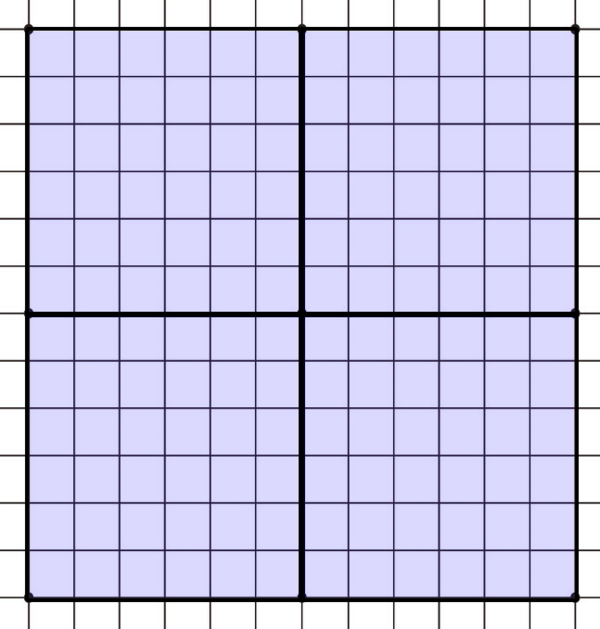
其次，一个围棋方格要映射为底层的M*M个生命游戏方格。如下图：

这张图中，一个淡紫色的大方格就是一个围棋的格点，它包含了5*5=25个生命游戏的小格点。生命游戏在这个小格点上运行。

游戏规则

游戏开始时，玩家在大方格上下棋。然后系统根据每个大方格点的情况，把它转化成生命游戏的状态。

比如某一个格点有一个黑子，那么系统会将这个大格点对应的小格点上随机撒上黑色的格点作为初始状态。当一个大格点有一个白色棋子，那么系统将会在这个大格点上撒上随机的红色的格点作为初始状态。然后生命游戏就开始演化。当一些Pattern（例如滑翔机）跨越了大格点的边界的时候，它就可以对对方的棋子进行攻击。

当某一个大格点的黑色方格大于红色个方格数之后，这个大格点的围棋子就会是黑色无论这个格点以前是否是黑色。而如果一个大格点原始没有棋子，则如果生命游戏的Pattern进入这个区域将不会对这个大格点造成任何影响。

最后，当围棋下完了之后，我们将根据小格点世界里面生命游戏的黑、红色元胞数来判断输赢。

关键参数

这个游戏将会有两个关键参数

空间尺度：一个大棋子对应多少小方格M

这是一个关键参数。当M较大的时候，底层的生命游戏规则将不会对围棋规则造成太实质的影响。当M较小的时候，整个游戏将变成生命游戏。

时间尺度：生命游戏世界演化速率T

假如不考虑计算机的运算速度，玩家下一步的时间如果为u，那么这段时间内，生命游戏演化的步数T就是一个关键变量。因为，如果T过大，则生命游戏的时间尺度就会过大，如果T小，那么生命游戏规则将来不得体现，围棋的时间尺度就会更大。总之，连续地调节T将会带来完全不同效果的游戏。

具体实施

技术选型

云服务：阿里云

Web

技术栈：Node.js + Express4 + Html5 + Canvas

实时通信：Socket.io （考虑迁移使用LeanCloud的实时通信SDK）

模块化：RequireJS

项目构建：Grunt

实施难点

最大的问题可能来自于大规模快速运行生命游戏所带来的性能问题。当M较大的时候，生命游戏的格点就会非常多，因此运行这么多方格的生命游戏就有可能会比较慢。

初步框架

先开发Web版本，前期集中对核心规则进行打磨，快速迭代MVP（最小化可行产品），收集玩家反馈，基本成型时逐步开发Android和iOS版本，过程中不断优化游戏体验。

以游戏机制、规则为核心，从职能分工上主要分为以下板块：

• 游戏策划设计
• Web开发
• Android开发
• iOS开发
• 美术动画设计
• 音乐设计
• 人机对弈AI、机器学习
• 测试

延伸

计算系统的开放性

无论是人工智能、涌现计算还是元胞自动机，这些已知的计算模式都存在着一个局限：它们都是封闭的计算系统。很多学者认为，正是因为这类计算系统不够开放，所以这些人工系统的复杂性还远远不能与真实世界中的复杂性相媲美[1]。

提到系统的开放性与封闭性，很多人会联想到热力学第二定律[2]。该定律指出，任何一个封闭系统必然会朝向最无序的熵增状态发展。但是，物理中的封闭系统是指不与外界进行能量、物质交换的系统。严格来讲，任何一个计算系统都不算封闭系统，因为计算系统需要外界的能量流注入以支持它完成计算。所以，我们不能简单套用物理中的热力学第二定律。

与能量和物质系统的开放性不同，计算系统的开放性是指程序在运行的过程中允许从外界输入信息，从而改变程序原始的运行轨迹的性质。比如Windows的“扫雷游戏”就是一个开放的计算系统，因为计算程序的运行必须要求用户的信息输入（操作）；而“生命游戏”元胞自动机则是一个封闭的系统，因为一旦该程序运行起来之后，外界就不能再干预该系统的运作了。

我们通常所说的系统的外界环境往往指我们所面对的大千世界。然而，当我们考虑计算系统的外界环境的时候，情况可能不必要这么复杂。因为计算机都是人类的工具，任何一个计算系统的设计归根结底都是为了满足人类使用者的需要。所以，计算系统的外界环境通常是指它的使用者——人（或者称为用户User、玩家Player）。当我们提到计算系统的开放性的时候，实际上我们讨论更多的是一种人——使用者和机器——计算系统之间的关系。

计算机游戏的逻辑内核

在这一小节，我们透过各种眼花缭乱的游戏外形，从计算程序的角度来理解计算机游戏。可以不夸张的说，无论是炫酷的3D游戏，还是小巧的手机游戏，它们都共享一个非常基本的逻辑内核：一个开放的动力学系统（Open Dynamical System）。

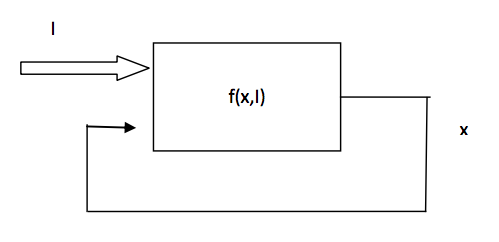
具体来说，我们可以把任何一个游戏看作一个模拟的世界。这样，随着CPU时钟的每一次嘀嗒跳动，这个游戏世界就运行一个仿真周期，游戏根据程序算法完成世界状态的更新。而游戏与模拟程序最大的不同就在于游戏允许玩家的输入，因此，我们可以把游戏的逻辑内核看作是一个简单的框图：

开放式的动力系统

每一个时间步，游戏程序根据用户的输入信息I以及游戏的状态x完成一次运算f(x,I)，这个运算结果反映为游戏新一步的状态，而这个状态又会在下一步反馈给系统。游戏的进度就体现在每个周期的x变量的不同。而游戏的规则则体现为f的不同。通常情况下，f不能写出解析的函数形式，而必须用算法的语言进行表达：它往往包含了游戏逻辑、人工智能、物理模拟、图形渲染等功能。

从数学上看，一个函数迭代：xt+1=f(xt)是一个标准的动力系统（Dynamical System）[8]。但是，该框图与动力系统最大的不同在玩家输入I的存在，因此我们称此框图表达的是一种开放式的动力系统（Open Dynamical System）。玩家输入信息I对于动力系统的设计者来说完全是不确定的（不包含在规则f之内），所以这种开放式的计算系统具有天然的不确定性。

值得指出的是，在随机动力系统的研究中，系统的运行外界随机因素的干扰。但是，在游戏中，外界输入的信息是玩家的游戏行为，它显然不能等同于一种随机干扰因素。因此，开放动力系统与随机动力系统是不同的。

总之，无论计算机游戏的形式多么复杂多变，它的最小逻辑内核却是不变的，也就是一个包含了玩家更新信息的开放式动力系统。

可玩性的涌现

游戏的可玩性目前仍然是一个含糊的概念，它就是指一个游戏可玩的程度。但是我们很难从定量的角度来衡量它。粗略地说，游戏的可玩性体现为人类在进行游戏过程中的愉悦性或者持久性。虽然游戏的图形设计、音响效果能够提高它的可玩性，但是游戏的本质则更多地体现为游戏规则层面。

在通常情况下，好玩的游戏通常依赖于那些设计简单，但是变化无穷的游戏规则，少既是多。一个最好的例子就是中国的围棋游戏。

围棋的规则异常简单：黑、白两个玩家交替下棋，当黑色或者白色棋子在几何空间上将另一方棋子包围住就可以把对方的棋子吃掉。最后，通过计算黑白双方的占地面积来判断输赢。

众所周知，这种简单游戏规则蕴含着极其丰富的走法。而复杂的走法并来源规则本身，而是来源于双方玩家在规则的限定下开发出来的策略。也就是说复杂的走法是从简单的限定规则中涌现而出的。因此，可以说围棋是一种涌现计算系统，只不过这个计算系统不是封闭的计算系统，而是一种开放式的允许两个玩家参与的系统。

比较中国围棋和第四章介绍的“生命游戏”程序会发现，它们二者具有一定的相似性。首先，它们都有一个棋盘格世界（即二维世界），其次它们都涉及非常有限的格子状态（“生命游戏”中的格子有黑、白两种状态；围棋的格子（确切说是线的交点）有黑、白、空三种状态）；再有，“生命游戏”和围棋的规则都是局部作用的。每一个方格或者棋子都仅仅对它周围的邻居方格或者棋子造成影响。最后，复杂的、长程的相互作用会在这些局部作用中涌现而出。也就是说，涌现性是围棋和“生命游戏”的最大共同点。

虽然可玩性和涌现性一样是一个无法说清的概念。但是通过游戏设计师们大量的实践摸索，人们渐渐发现要想设计出具有可玩性的游戏，规则中的平衡性[9][10]是一个必不可少的因素。这里，平衡性通常是指游戏的规则或者游戏过程中所体现出来的对称性、均匀性和公平性。

举例来说，围棋的黑棋、白棋在一开始就处于一种完全均匀、公平的状态。再如，很多格斗游戏（例如街头霸王）在不同的角色之间就存在着一种平衡性。

但是，均匀性和对称性仅仅构成了游戏平衡性的一个重要因素，另一方面，游戏必须是一个动态的平衡系统，也就是说游戏本身要存在一种破坏游戏平衡的机制（也就是所谓的对称破缺机制）。

让我们仍然用围棋为例，虽然在初始时刻，黑白双方完全处于对称、均匀的地位。但是一旦某一方吃掉了另一方的一大片棋子之后，这种对称性就会在瞬间破缺掉，被吃掉棋子的一方会一下子占据被动地位。正是这样一种打破平衡的机制才使得游戏的可玩性持续的提高。

另外一个例子来源于俄罗斯方块。玩家在游戏的过程中总是要追求一种平衡（落下的物块应该足够均匀的分布，以便能够消掉大量的物块），但是这种平衡很容易就会被新掉下来的物块打破。这样，玩家的游戏过程就体现为一种不断地建立平衡、打破平衡的重复之中。正是这样一种动态的平衡机制使得俄罗斯方块具有很高的可玩性。

当然，游戏中的这种平衡、打破平衡的机制应调节到一定的比例范围内才会好玩。过于均衡的游戏会很容易让玩家生厌，而过多地破坏平衡机制则会让玩家丧失信心。所以，正如复杂的行为诞生于“混沌边缘”的计算系统一样，游戏中的这种建立平衡、打破平衡的交替性也应处在某种“混沌边缘”的临界状态下才能使得游戏的可玩性增加。

总之，游戏中的可玩性是一个非常值得深入探索的概念。

Facebook进军智能围棋

参考阅读：Facebook进军智能围棋 欲造新深蓝击败人类

众所周知，计算机打败象棋和国际象棋对于目前来说已经不是新闻，但在围棋领域计算机的水平却和高手似乎有着一道不可逾越的鸿沟。如今，facebook正在启动一项计划，帮助计算机找到正确的学习围棋的途径，希望以此打造一款围棋界的“深蓝”，帮助人工智能击败人类顶尖的围棋高手。

90年代中期，一个叫Chinook计算机程序在跳棋比赛中击败世界头号选手。三年后，IBM的深蓝超级计算机在国际象棋比赛中战胜世界冠军加里卡斯帕罗夫。2011年，另一个IBM机器，华生，使最聪明的人类处于危险之中！机器已经可以在广泛领域的智力测试中击败聪明的人类，从游戏到奥赛罗。但有一项游戏仍然是我们人类代表着顶尖水平，那就是围棋。

在所有其他的游戏中，计算机都可以在本质上分析各种可能出现的结果。的确，国际象棋特级大师卡斯帕罗夫也能推算出可能出现的结果，以类似的方式。但一台机器可以算出比卡斯帕罗夫更多的未来动作。同样，一台机器可以在围棋对弈时向前看，但在这种情况下，计算变得困难得多。在一个19乘19的围棋盘上，玩家将棋子放在两条线的交叉点上，去确定这手棋的价值是极其复杂的，甚至是神秘的。顶级的围棋高手会告诉你，他们的落子选择，在某种程度上，是潜意识。让一台电脑用这种方式计算完全是另一种任务，你不能用同样的方法去创造一台深蓝或华生。

有了这样的想法，脸谱网的研究人员现在通过研究围棋来学习和了解人工智能形式：深度学习。

参考文献

Jake 计算机游戏——开放的计算系统]

Category：复杂系统 Category：旧词条迁移