“反应扩散模型和亚种群模型”的版本间的差异
| 第3行: | 第3行: | ||
== 反应扩散过程 == | == 反应扩散过程 == | ||
| + | |||
| + | [[File:Snipaste_2020-10-23_22-40-33.png|thumb|right|(a) Schematic illustration of the simplified modeling framework based on the particle-network scheme. At the macroscopic level the system is composed of a heterogeneous network of subpopulations. The contagion process in one subpopulation can spread to other subpopulations because of particles diffusing across subpopulations. (b) At the microscopic level, each subpopulation contains a population of individuals. The dynamical process, for instance, a contagion phenomenon, is described by a simple compartmentalization (compartments are indicated by different colored dots in the picture). Within each subpopulation, individuals can mix homogeneously or according to a subnetwork and can diffuse with probability p from one subpopulation to another following the edges of the network. (c) A critical value $p_c$ of the individuals or particles diffusion identifies a phase transition between a regime in which the contagion affects a large fraction of the system and one in which only a small fraction is affected.]] | ||
| + | |||
More in general models of social behavior and human mobility are often framed as reaction-diffusion processes where each node $i$ is allowed to host any nonnegative integer number of particles $\mathcal{N}(i)$, so that the total particle population of the system is $\mathcal{N}=\sum_i\mathcal{N}(i)$. This particle-network framework considers that each particle diffuses along the edges connecting nodes with a diffusion coefficient that depends on the node degree and/or other node attributes. Within each node particles may react according to different schemes characterizing the interaction dynamics of the system. A simple sketch of the particle-network framework is represented in the Figure. | More in general models of social behavior and human mobility are often framed as reaction-diffusion processes where each node $i$ is allowed to host any nonnegative integer number of particles $\mathcal{N}(i)$, so that the total particle population of the system is $\mathcal{N}=\sum_i\mathcal{N}(i)$. This particle-network framework considers that each particle diffuses along the edges connecting nodes with a diffusion coefficient that depends on the node degree and/or other node attributes. Within each node particles may react according to different schemes characterizing the interaction dynamics of the system. A simple sketch of the particle-network framework is represented in the Figure. | ||
| 第65行: | 第68行: | ||
其中$\bar{S}(t)=\sum_k P(k)S_k$。 | 其中$\bar{S}(t)=\sum_k P(k)S_k$。 | ||
| + | |||
| + | == 参考文献 References == | ||
| + | {{reflist}} | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <small>此页参考来源: Pastor-Satorras R, Castellano C, Van Mieghem P, et al. Epidemic processes in complex networks[J]. Reviews of modern physics, 2015, 87(3): 925. | ||
2020年10月23日 (五) 22:43的版本
此词条暂由Potatozh初译,未经审校,带来阅读不便,请见谅。
反应扩散过程
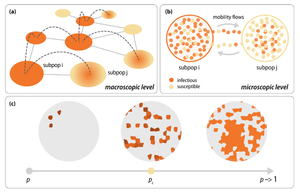
More in general models of social behavior and human mobility are often framed as reaction-diffusion processes where each node $i$ is allowed to host any nonnegative integer number of particles $\mathcal{N}(i)$, so that the total particle population of the system is $\mathcal{N}=\sum_i\mathcal{N}(i)$. This particle-network framework considers that each particle diffuses along the edges connecting nodes with a diffusion coefficient that depends on the node degree and/or other node attributes. Within each node particles may react according to different schemes characterizing the interaction dynamics of the system. A simple sketch of the particle-network framework is represented in the Figure.
一般来说,社会行为和人类流动性模型经常被构建为反应扩散过程,其中每个节点$i$可以容纳任何非负整数$\mathcal{N}(i)$个粒子,因此系统的总粒子数为$\mathcal{N}=\sum_i\mathcal{N}(i)$。 该粒子——网络框架中的节点内的每个粒子只能沿着连接节点的连边扩散,扩散系数取决于节点度或其他节点属性等。不同系统里的节点内的粒子的反应规则不同。粒子——网络的框架简单示意图如图所示。
In order to have an analytic description of reaction-diffusion systems in networks one has to allow the possibility of heterogeneous connectivity patterns among nodes. A first analytical approach to these systems considers the extension of the degree-based mean-field approach to reaction-diffusion systems in networks with arbitrary degree distribution. For simplicity, we first consider the DBMF approach to the case of a simple system in which noninteracting particles (individuals) diffuse on a network with arbitrary topology. A convenient representation of the system is therefore provided by quantities defined in terms of the degree k:
为了对网络中的反应扩散系统进行理论上的分析描述,我们允许节点之间具有异质的连接模式。对这些系统的第一种分析方法是考虑将基于度的平均场理论方法扩展到具有任意度分布的网络中的反应扩散系统。简单起见,首先考虑一个任意网络结构的简单系统,其中粒子间没有相互作用或反应,粒子只会在网络上扩散的的情况。因此,通过以度$k$来分类的话,可以将系统简单表示为: \begin{equation} \mathcal{N}_k=\frac{1}{N_k}\sum_{i\in\mathcal{V}(k)}\mathcal{N}(i) \end{equation} where $N_k=NP(k)$ is the number of nodes with degree $k$ and the sum runs over the set of nodes $\mathcal{V}(k)$ having degree equal to k. The degree block variable $\mathcal{N}_k$ represents the average number of particles in nodes with degree k. The use of the DBMF approach amounts to the assumption that nodes with degree k, and thus the particles in those nodes, are statistically equivalent. In this approximation the dynamics of particles randomly diffusing on the network is given by a mean-field dynamical equation expressing the variation in time of the particle subpopulation N kðtÞ in each degree block k. This can be easily written as
其中$N_k=NP(k)$表示度为k的节点数量,$\mathcal{V}(k)$表示度为$k$的节点集合,$\mathcal{N}_k$表示度为$k$的节点的平均粒子数。基于度的平均场理论假设度为$k$的节点,同理节点中的粒子,在统计上是等效的。在这种近似的假设下,粒子随机扩散的动力学可以由如下平均场理论方程表示: \begin{equation} \frac{d\mathcal{N}_k}{dt}=-d_k\mathcal{N}_k(t)+k\sum_{k'}P(k'|k)d_{k'k}\mathcal{N}_{k'}(t) \end{equation} The first term of the equation considers that only a fraction $d_k$ of particles moves out of the node per unit time. The second term instead accounts for the particles diffusing from the neighbors into the node of degree k. This term is proportional to the number of links k times the average number of particles coming from each neighbor. This is equal to the average over all possible degrees $k'$ of the fraction of particles moving on that edge, $d_{k'k}$, according to the conditional probability $P(k'|k)$ that an edge belonging to a node of degree k is pointing to a node of degree $k'$. Here the term $d_{k'k}$ is the diffusion rate along the edges connecting nodes of degree k and $k'$. In the simplest case of homogeneous diffusion each particle diffuses with rate $r$ from the node in which it is and thus the diffusion per link $d_{k'k}=r/k'$. On uncorrelated networks $P(k'|k)=k'P(k')/\left<k\right>$ and hence one easily gets in the stationary state $d\mathcal{N}/dt=0$ the solution (Noh and Rieger, 2004; Colizza, Pastor-Satorras, and Vespignani, 2007)
方程中的第一项表示每单位时间内有$d_k$部分的粒子从度为$k$的节点中离开,第二项表示粒子从邻居节点扩散到度为$k$的节点中,该项与连边数$k$成正比。条件概率$P(k'|k)$表示的是一条边的一端连接度为$k$的节点时,其另一端指向度为$k'$的概率。$d_{k'k}$表示的是两端连接了度为$k$和$k'$节点的连边的扩散率。在均匀扩散的最简单情况下,每个粒子从其所在的节点以速率$r$扩散,因此沿着每条连边的扩散率为$d_{k'k}=r/k'$。在无关联的网络上,$P(k'|k)=k'P(k')/\left<k\right>$,因此在稳态$d\mathcal{N}/dt=0$时,很容易得到解(Colizza等,2007b; Noh和Rieger,2004): \begin{equation} \mathcal{N}_k=\frac{k}{\left<k\right>}\frac{\mathcal{N}}{N} \end{equation} The above equation explicitly brings the diffusion of particles in the description of the system and points out the importance of network topology in reaction-diffusion processes. This expression indicates that the larger the degree of a node, the larger the probability to be visited by the diffusing particles.
上式显式地给出了系统中粒子扩散的描述,并指出网络拓扑结构在反应扩散过程中的重要性。从式中可以看到,一个节点的度越大,则其被扩散中的粒子访问的可能性就越大。
亚种群模型
The above approach can be generalized to reacting particles with different states by adding a reaction term to the above equations (Colizza, Pastor-Satorras, and Vespignani, 2007). We now describe a generalization to this setting of the standard SIS model in discrete time, with probability per unit time $\beta$ of infection and probability $\mu$ of recovery. We consider $\mathcal{N}$ individuals diffusing in a heterogeneous network with $N$ nodes and degree distribution $P(k)$. Each node i of the network has a number $I(i)$ of infectious and $S(i)$ of susceptible individuals. The occupation numbers $I(i)$ and $S(i)$ can have any integer value, including $I(i)=S(i)=0$, that is, void nodes with no individuals. This modeling scheme describes spatially structured interacting subpopulations, such as city locations, urban areas, or defined geographical regions (Grenfell and Harwood, 1997; Hanski and Gaggiotti, 2004) and is usually referred to as the metapopulation approach. Each node of the network represents a subpopulation and the compartment dynamics accounts for the possibility that individuals in the same location may get into contact and change their state according to the infection dynamics. The interaction among subpopulations is the result of the movement of individuals from one subpopulation to the other. We have thus to associate with each individual’s class a diffusion probability $p_I$ and $p_S$ that indicates the probability for any individual to leave its node and move to a neighboring node of the network. In general the diffusion probabilities are heterogeneous and can be node dependent; however, for simplicity we assume that individuals diffuse with probability $p_I=p_S=1$ along any of the links departing from the node in which they are. This implies that at each time step an individual sitting on a node with degree k will diffuse into one of its nearest neighbors with probability $1/k$. In order to write the dynamical equations of the system we define the following quantities:
通过将反应项添加到上述方程中,可以将上述方法推广到具有不同状态的粒子发生反应的情形(Colizza等,2007b)。现在,我们描述在该情形下的SIS模型情况,其中单位时间的感染概率为$\beta$,恢复概率为$\mu$。我们考虑在具有$N$个节点和度分布为$P(k)$的异质网络中扩散的$\mathcal{N}$个个体。网络的每个节点$i$分别具有$I(i)$个感染态个体和$S(i)$个易感态个体(取值为非负整数值)。这种建模体系描述了空间结构相互作用的亚种群,例如城市位置、城市区域或确定的地理区域(Gren fall和Harwood,1997; Hanski和Gaggiotti,2004),并且通常被称为亚种群方法。网络中的每个节点代表一个亚种群,仓室动力学表示了处于相同位置的个体可能会相互接触并根据系统对应的感染动力学改变自身的状态的可能性。亚群之间的相互作用是个体从一个亚种群迁移到另一个亚种群的结果。为简单起见,我们可以假设个体从他们所在的节点离开沿着任意一条连边扩散的概率为$p_I=p_S=1$。这意味着每个时间步,度为$k$的节点上的一个个体将以概率$1/k$扩散到其最近的邻居之一。为了得到系统的动力学方程,我们定义如下的量: \begin{equation} I_k=\frac{1}{N_k}\sum_{i\in\mathcal{V}(k)}I(i) \end{equation} \begin{equation} S_k=\frac{1}{N_k}\sum_{i\in\mathcal{V}(k)}S(i) \end{equation}
where the sums $\sum_{i\in\mathcal{V}(k)}$ are performed over nodes of degree $k$. These two quantities express the average number of susceptible and infectious individuals in nodes with degree $k$. Clearly, $\mathcal{N}_k=I_k+S_k$ is the average number of individuals in nodes with degree $k$. These quantities allow one to write the discrete-time equation describing the time evolution of $I_k(t)$ for each class of degree k as
其中$\mathcal{V}(k)$表示度为$k$的节点集合。上面的两式表示的是度为$k$的节点的平均感染态和易感态个体数,显然有$\mathcal{N}_k=I_k+S_k$。因此,系统的动力学方程可以表示为 \begin{equation} I_k(t+1)=k\sum_{k'}P(k|k')\frac{1}{k'}[(1-\mu)I_{k'}(t)+\beta\Gamma_{k'}(t)] \end{equation} where $\Gamma_{k'}(t)$ is an interaction kernel, a function of $I_{k'}$ and $S_{k'}$. The above equation is obtained by considering that at each time step the particles present on a node of degree $k$, first react, and then diffuse away from the node with probability 1. The value of $I_k(t+1)$ is obtained by summing the contribution of all particles diffusing to nodes of degree k from their neighbors of any degree $k'$, including the new particles generated by the reaction term $\Gamma_{k'}$. In the case of uncorrelated networks, the above equation reduces to
其中$\Gamma_{k'}(t)$为相互作用的核,是关于$I_{k'}$和$S_{k'}$的函数。该方程是通过考虑在每个时间步,度为$k$的节点上的粒子先发生反应,然后以1的概率从节点扩散出去得到的。在无关联网络的情况下,上式可以写为 \begin{equation} I_k(t+1)=\frac{k}{\left<k\right>}[(1-\mu)\bar{I}(t)+\beta\Gamma] \end{equation} where $\bar{I}(t)=\sum_k P(k)I_k$ is the average number of infected individuals per node in the network and $\Gamma=\sum_k P(k)\Gamma_k$. Analogously the equation describing the dynamics of susceptible individuals is
其中$\bar{I}(t)=\sum_k P(k)I_k$表示网络中每个节点的平均感染态个体的数量。$\Gamma=\sum_k P(k)\Gamma_k$。类似地,易感态个体的动力学方程可以表示为 \begin{equation} S_k(t+1)=\frac{k}{\left<k\right>}[\bar{S}(t)+\mu\bar{I}(t)-\beta\Gamma] \end{equation} where $\bar{S}(t)=\sum_k P(k)S_k$.
其中$\bar{S}(t)=\sum_k P(k)S_k$。
参考文献 References
此页参考来源: Pastor-Satorras R, Castellano C, Van Mieghem P, et al. Epidemic processes in complex networks[J]. Reviews of modern physics, 2015, 87(3): 925.