“顶点”的版本间的差异
(→外链) |
|||
| 第47行: | 第47行: | ||
* {{Cite book |author1=Harary, Frank |author2=Palmer, Edgar M. | title=Graphical enumeration | date=1973 | publisher=New York, Academic Press | location= | isbn=0-12-324245-2 | pages=}} | * {{Cite book |author1=Harary, Frank |author2=Palmer, Edgar M. | title=Graphical enumeration | date=1973 | publisher=New York, Academic Press | location= | isbn=0-12-324245-2 | pages=}} | ||
==外链== | ==外链== | ||
| − | + | *{{mathworld | title = Graph Vertex | urlname = GraphVertex}} | |
2020年10月23日 (五) 22:55的版本
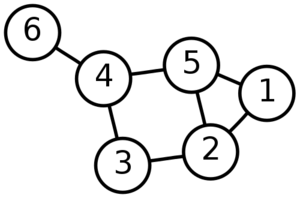
一个具有6个 顶点和7条边的图,其中最左边数字6的结点是 叶顶点 Leaf Vertex或叫做 悬挂点 Pendant Vertex
在数学上,更具体地说在图论中, 顶点或 节点是形成图的基本单位: 无向图由一组 顶点和一组边(无序 顶点对)组成,而 有向图由一组 顶点和一组弧(有序 顶点对)组成。在图的图解表示中, 顶点通常用带标签的圆来表示,而边则用从一个 顶点延伸到另一个 顶点的直线或箭头来表示。
从图论的观点来看, 顶点被视为无特征且不可分割的对象。但是根据图的应用场景, 顶点可能有额外的结构。 例如: 语义网络(计算机科学) ,其中的 顶点表示概念或对象的类。
形成边的两个 顶点被称为这条边的 端点,这条边称为 关联Incident于这两个 顶点的边。如果图包含一条边(v,w) ,则称一个 顶点w 与另一个 顶点 v 相邻接 Adjacent 。 顶点 v 的邻域(neighborhood)是该图的一个 导出子图(induced subgraph),由邻接于 "v" 的所有 顶点构成。
顶点类型
用具有8个顶点(其中一个是孤立的)和10条边的网络示意。
图中顶点的度数(用𝛿(v)表示)是关联到它的边的数目。一个孤立顶点是一个度为零的顶点,也就是说,是一个不是任何边的端点的顶点(示例图片中有一个孤立顶点的例子)。[1]叶顶点(也称作悬挂点)是度数为1的顶点。在有向图中,我们可以区分外度(外出边数)(用 𝛿 +(v) 表示),和外度(外入边数) (用𝛿−(v)表示) ; 源顶点是外度为零的顶点,而汇顶点是具有外度为零的顶点。单纯形顶点是邻接成团的顶点:每两个邻接都是相邻的。通用顶点是在图中与其他所有顶点都相邻的顶点。
割点是一类顶点,如果去掉它,就会断开剩余图的连接; 顶点分隔符是一组顶点的集合,如果去掉这些顶点,就会将剩余图断裂成小片段。一个k- 顶点连通图是指一类去掉少于 k 个顶点后,剩余部分仍然连通的图。一个独立的集合是一组任意二者均不相邻的顶点群。顶点覆盖是一组顶点,它们均包含图中任意边的至少一个端点。图的顶点空间是一个向量空间,它的基向量与图的顶点相对应。
如果一个图具有将任何顶点映射到任何其他顶点的对称性,则该图是顶点传递的。在图计数和图同构的情况下,区分标记顶点和非标记顶点非常重要。标记顶点是与能使其区别于其他标记顶点的额外信息相关联的顶点; 只有当其顶点之间的对应关系与有相同标记的顶点配对时,两个图才可以被认为是同构的。非标记顶点是仅基于其在图中的邻接顶点而不基于任何其他信息就能被其他任意顶点替换的一类顶点。
在图中的顶点类似但不等同于多面体的顶点:多面体的骨架构成一个图,其顶点是多面体的顶点,但多面体的顶点有无法在图论中假定存在的其他结构(几何位置) 。多面体中顶点的顶点图形类似于图中顶点的邻域。
参见
参考文献
- ↑ File:Small Network.png; example image of a network with 8 vertices and 10 edges
- Berge, Claude, Théorie des graphes et ses applications. Collection Universitaire de Mathématiques, II Dunod, Paris 1958, viii+277 pp. (English edition, Wiley 1961; Methuen & Co, New York 1962; Russian, Moscow 1961; Spanish, Mexico 1962; Roumanian, Bucharest 1969; Chinese, Shanghai 1963; Second printing of the 1962 first English edition. Dover, New York 2001)
- Chartrand, Gary (1985). Introductory graph theory. New York: Dover. ISBN 0-486-24775-9. https://archive.org/details/introductorygrap0000char.
- Biggs, Norman; Lloyd, E. H.; Wilson, Robin J. (1986). Graph theory, 1736-1936. Oxford [Oxfordshire]: Clarendon Press. ISBN 0-19-853916-9.
- Harary, Frank (1969). Graph theory. Reading, Mass.: Addison-Wesley Publishing. ISBN 0-201-41033-8.
- Harary, Frank; Palmer, Edgar M. (1973). Graphical enumeration. New York, Academic Press. ISBN 0-12-324245-2.
外链
本中文词条由鲁鱼陶阴 参与编译,不是海绵宝宝编辑,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。