“层次聚类”的版本间的差异
标签:移动网页编辑 移动版编辑 |
|||
| 第1行: | 第1行: | ||
此词条暂由水流心不竞翻译,未经审校,带来阅读不便,请见谅。由CecileLi初步审校。翻译评级:B | 此词条暂由水流心不竞翻译,未经审校,带来阅读不便,请见谅。由CecileLi初步审校。翻译评级:B | ||
| − | |||
| − | + | 在[[数据挖掘]]和[[统计学]]中,'''<font color="#ff8000"> 层次聚类 Hierarchical clustering</font>'''(也被称为“层次数据聚类或”“HCA”)是一种通过建立一个集群层次结构来[[聚类分析]]的方法。实现层次聚类的方法通常有两种:<ref name="clusteringMethods">Rokach, Lior, and Oded Maimon. "Clustering methods." Data mining and knowledge discovery handbook. Springer US, 2005. 321-352.</ref> | |
| − | + | * '''凝聚聚类 Agglomerative''':这是一种“自上而下又自下而上/纵向”的方法:每个被观察数据从自己的簇类中开始,当一个观察组数据向上层移动时,成对的簇类集群被合并。 | |
| − | + | * '''分裂聚类 Divisive''': 这是一种“自上而下”的方法:所有的被观察数据都从一个簇类集群中开始,当一个簇类向下移动时,整个观察组数据群会递归地执行分割。 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | * '''Divisive''': | ||
| − | |||
| − | |||
In general, the merges and splits are determined in a [[greedy algorithm|greedy]] manner. The results of hierarchical clustering<ref>{{cite book | author=Frank Nielsen | title=Introduction to HPC with MPI for Data Science | year=2016 | publisher=Springer | | In general, the merges and splits are determined in a [[greedy algorithm|greedy]] manner. The results of hierarchical clustering<ref>{{cite book | author=Frank Nielsen | title=Introduction to HPC with MPI for Data Science | year=2016 | publisher=Springer | | ||
| − | |||
| − | |||
补充:此处翻译编辑视图内有显示阅读视图中无。 | 补充:此处翻译编辑视图内有显示阅读视图中无。 | ||
| − | + | 一般来说,合并和分裂是以使用者希望的方式决定的。而层次聚类的结果 <ref>{{cite book | author=Frank Nielsen | title=Introduction to HPC with MPI for Data Science | year=2016 | publisher=Springer |chapter=Chapter 8: Hierarchical Clustering | url=https://www.springer.com/gp/book/9783319219028 |chapter-url=https://www.researchgate.net/publication/314700681 }}</ref> 通常在树状图中呈现。 | |
| − | |||
| − | chapter=Chapter 8: Hierarchical Clustering | url=https://www.springer.com/gp/book/9783319219028 |chapter-url=https://www.researchgate.net/publication/314700681 }}</ref> | ||
| − | |||
| − | + | '''<font color="#ff8000"> 层次凝聚聚类 Hierarchical agglomerative clustering</font>'''(HAC)的标准算法的[[时间复杂度]]为<math>\mathcal{O}(n^3)</math> ,并且需要 <math>\mathcal{O}(n^2)</math> 占用内存,这使得它对于中等数据集来说效率太低了。然而,对于某些特殊情况,已知的最有效凝聚方法(复杂度 <math>\mathcal{O}(n^2)</math>)是: SLINK 用于单连接<ref name="SLINK">{{cite journal | author=R. Sibson | title=SLINK: an optimally efficient algorithm for the single-link cluster method | journal=The Computer Journal | volume=16 | issue=1 | pages=30–34 | year=1973 | publisher=British Computer Society | url=http://www.cs.gsu.edu/~wkim/index_files/papers/sibson.pdf | doi=10.1093/comjnl/16.1.30}}</ref> for [[Single-linkage clustering|single-linkage]], CLINK用于完全连接<ref name="CLINK">{{cite journal | author=D. Defays | title=An efficient algorithm for a complete-link method | journal=The Computer Journal | volume=20 | issue=4 | pages=364–366 | year=1977 | publisher=British Computer Society | url=http://comjnl.oxfordjournals.org/content/20/4/364.abstract | doi=10.1093/comjnl/20.4.364| doi-access=free }}</ref>[[complete-linkage clustering]]。一般情况下的运行时可以缩减为 <math>\mathcal{O}(n^2 \log n)</math> ,代价是进一步增加内存需求。在多数情况下,这种方法的内存消耗太大,并不实用。 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Except for the special case of single-linkage, none of the algorithms (except exhaustive search in <math>\mathcal{O}(2^n)</math>) can be guaranteed to find the optimum solution. | Except for the special case of single-linkage, none of the algorithms (except exhaustive search in <math>\mathcal{O}(2^n)</math>) can be guaranteed to find the optimum solution. | ||
| − | + | 除了单连接的特殊情况外,所有算法(除了<math>\mathcal{O}(2^n)</math>数学中的穷举搜索)都不能保证找到最优解。 | |
| − | |||
Divisive clustering with an exhaustive search is <math>\mathcal{O}(2^n)</math>, but it is common to use faster heuristics to choose splits, such as k-means. | Divisive clustering with an exhaustive search is <math>\mathcal{O}(2^n)</math>, but it is common to use faster heuristics to choose splits, such as k-means. | ||
| − | + | 穷举搜索的分裂群集是 <math>\mathcal{O}(2^n)</math>,但是通常使用运算速度更快的探索法来选择分裂,比如[[k-means]]。 | |
| − | |||
| − | == Cluster dissimilarity | + | ==簇异性 Cluster dissimilarity== |
In order to decide which clusters should be combined (for agglomerative), or where a cluster should be split (for divisive), a measure of dissimilarity between sets of observations is required. In most methods of hierarchical clustering, this is achieved by use of an appropriate [[metric (mathematics)|metric]] (a measure of [[distance]] between pairs of observations), and a linkage criterion which specifies the dissimilarity of sets as a function of the pairwise distances of observations in the sets. | In order to decide which clusters should be combined (for agglomerative), or where a cluster should be split (for divisive), a measure of dissimilarity between sets of observations is required. In most methods of hierarchical clustering, this is achieved by use of an appropriate [[metric (mathematics)|metric]] (a measure of [[distance]] between pairs of observations), and a linkage criterion which specifies the dissimilarity of sets as a function of the pairwise distances of observations in the sets. | ||
| 第71行: | 第38行: | ||
| − | === Metric | + | ===度量标准 Metric=== |
| − | + | ''更多信息请查看[[度量标准 Metric]]'' | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
The choice of an appropriate metric will influence the shape of the clusters, as some elements may be close to one another according to one distance and farther away according to another. For example, in a 2-dimensional space, the distance between the point (1,0) and the origin (0,0) is always 1 according to the usual norms, but the distance between the point (1,1) and the origin (0,0) can be 2 under Manhattan distance, <math>\scriptstyle\sqrt{2}</math> under Euclidean distance, or 1 under maximum distance. | The choice of an appropriate metric will influence the shape of the clusters, as some elements may be close to one another according to one distance and farther away according to another. For example, in a 2-dimensional space, the distance between the point (1,0) and the origin (0,0) is always 1 according to the usual norms, but the distance between the point (1,1) and the origin (0,0) can be 2 under Manhattan distance, <math>\scriptstyle\sqrt{2}</math> under Euclidean distance, or 1 under maximum distance. | ||
| 第84行: | 第46行: | ||
| − | + | 一些常用的'''<font color="#ff8000"> 层次聚类 Hierarchical clustering</font>'''指标如下:<ref>{{cite web | title=The DISTANCE Procedure: Proximity Measures | url=https://support.sas.com/documentation/cdl/en/statug/63033/HTML/default/statug_distance_sect016.htm | work=SAS/STAT 9.2 Users Guide | publisher= [[SAS Institute]] | date= | accessdate=2009-04-26}}</ref> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{|class="wikitable" | {|class="wikitable" | ||
| − | + | ! 名字 | |
| − | + | ! 公式 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | !名字 | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ! | ||
| − | |||
|- | |- | ||
| − | + | | [[欧氏距离 Euclidean distance]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | | [[Euclidean distance]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| <math> \|a-b \|_2 = \sqrt{\sum_i (a_i-b_i)^2} </math> | | <math> \|a-b \|_2 = \sqrt{\sum_i (a_i-b_i)^2} </math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | + | | 平方欧氏距离 Squared Euclidean distance | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | Squared Euclidean distance | ||
| − | |||
| <math> \|a-b \|_2^2 = \sum_i (a_i-b_i)^2 </math> | | <math> \|a-b \|_2^2 = \sum_i (a_i-b_i)^2 </math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | + | | [[曼哈顿距离 Manhattan distance]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | | [[Manhattan distance]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| <math> \|a-b \|_1 = \sum_i |a_i-b_i| </math> | | <math> \|a-b \|_1 = \sum_i |a_i-b_i| </math> | ||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | + | | [[最大距离 Maximum distance]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | | [[ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| <math> \|a-b \|_\infty = \max_i |a_i-b_i| </math> | | <math> \|a-b \|_\infty = \max_i |a_i-b_i| </math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | + | | [[马氏距离 Mahalanobis distance]] | |
| + | | <math> \sqrt{(a-b)^{\top}S^{-1}(a-b)} </math> 其中''S''是[[协方差矩阵]] | ||
|- | |- | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|} | |} | ||
| − | |||
For text or other non-numeric data, metrics such as the [[Hamming distance]] or [[Levenshtein distance]] are often used. | For text or other non-numeric data, metrics such as the [[Hamming distance]] or [[Levenshtein distance]] are often used. | ||
For text or other non-numeric data, metrics such as the Hamming distance or Levenshtein distance are often used. | For text or other non-numeric data, metrics such as the Hamming distance or Levenshtein distance are often used. | ||
| − | + | 对于文本文字或其他非数字数据,常常使用[[汉明距离 Hamming distance]]或[[编辑距离 Levenshtein distance]]等度量标准。 | |
| − | A review of cluster analysis in health psychology research found that the most common distance measure in published studies in that research area is the Euclidean distance or the squared Euclidean distance.{{Citation needed|date=April 2009}} | + | A review of cluster analysis in health psychology research found that the most common distance measure in published studies in that research area is the Euclidean distance or the squared Euclidean distance. |
| + | |||
| + | 通过对数据聚类健康心理学研究的回顾发现,在该研究领域已发表的研究中,最常见的距离测量方法是欧几里得度量距离或欧几里得度量距离的平方。{{Citation needed|date=April 2009}} | ||
| − | |||
| − | |||
=== Linkage criteria 连接准则=== | === Linkage criteria 连接准则=== | ||
| − | |||
| − | |||
The linkage criterion determines the distance between sets of observations as a function of the pairwise distances between observations. | The linkage criterion determines the distance between sets of observations as a function of the pairwise distances between observations. | ||
| 第235行: | 第90行: | ||
| − | Some commonly used linkage criteria between two sets of observations ''A'' and ''B'' are | + | Some commonly used linkage criteria between two sets of observations ''A'' and ''B'' are: |
| − | |||
| − | |||
| − | |||
| − | |||
| − | {| | + | 两组观测值''A''和''B''之间一些常用的连接标准如下:<ref>{{cite web | title=The CLUSTER Procedure: Clustering Methods | url=https://support.sas.com/documentation/cdl/en/statug/63033/HTML/default/statug_cluster_sect012.htm | work=SAS/STAT 9.2 Users Guide | publisher= [[SAS Institute]] | date= | accessdate=2009-04-26}}</ref><ref>{{cite journal |last=Székely |first=G. J. |last2=Rizzo |first2=M. L. |year=2005 |title=Hierarchical clustering via Joint Between-Within Distances: Extending Ward's Minimum Variance Method |journal=Journal of Classification |volume=22 |issue=2 |pages=151–183 |doi=10.1007/s00357-005-0012-9 }}</ref> |
{|class="wikitable" | {|class="wikitable" | ||
| − | + | ! 名字 | |
| − | + | ! 公式 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | !名字 | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ! | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | + | | 最大或完全连接聚类 | |
| + | | <math> \max \, \{\, d(a,b) : a \in A,\, b \in B \,\}</math> | ||
|- | |- | ||
| − | + | | 最小或单连接聚类 | |
| − | | | + | | <math> \min \, \{\, d(a,b) : a \in A,\, b \in B \,\}</math> |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | <math> \ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | + | | 未加权平均链接聚类 Unweighted average linkage clustering (or [[UPGMA]]) | |
| − | + | | <math> \frac{1}{|A|\cdot|B|} \sum_{a \in A }\sum_{ b \in B} d(a,b)</math> | |
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | <math> | ||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | + | | 加权平均数链接聚类 Weighted average linkage clustering (or [[WPGMA]]) | |
| + | | <math> d(i \cup j, k) = \frac{d(i, k) + d(j, k)}{2} | ||
|- | |- | ||
| − | + | | 质心链接集群 Centroid linkage clustering, or UPGMC | |
| + | | <math> \|c_s - c_t \| </math> where <math>c_s</math> and <math>c_t</math> 分别是 ''s''类和 ''t''类的中心. | ||
|- | |- | ||
| − | + | | 最小能量聚类[[Energy distance|Minimum energy clustering]] | |
| − | | [[Energy distance|Minimum energy clustering]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| <math> \frac {2}{nm}\sum_{i,j=1}^{n,m} \|a_i- b_j\|_2 - \frac {1}{n^2}\sum_{i,j=1}^{n} \|a_i-a_j\|_2 - \frac{1}{m^2}\sum_{i,j=1}^{m} \|b_i-b_j\|_2 </math> | | <math> \frac {2}{nm}\sum_{i,j=1}^{n,m} \|a_i- b_j\|_2 - \frac {1}{n^2}\sum_{i,j=1}^{n} \|a_i-a_j\|_2 - \frac{1}{m^2}\sum_{i,j=1}^{m} \|b_i-b_j\|_2 </math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|} | |} | ||
| − | + | 其中 ''d'' 是选定的度量单位。其他连接准则包括: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | * The sum of all intra-cluster variance.所有簇内方差之和。 | |
| − | + | * The increase in variance for the cluster being merged 合并中的簇的方差相加([[Ward标准]])<ref name="wards method">{{cite journal|doi=10.2307/2282967|last=Ward |first=Joe H. |title=Hierarchical Grouping to Optimize an Objective Function |journal=Journal of the American Statistical Association |volume=58 |issue=301 |year=1963 |pages=236–244}}</ref>. | |
| − | + | * The probability that candidate clusters spawn from the same distribution function (V-linkage).候选数据群从同一分布函数(V-连锁)中产生的概率。 | |
| − | }}</ref> | + | * The product of in-degree and out-degree on a k-nearest-neighbour graph (graph degree linkage).k-最近邻图(图度连锁)上的入度与出度的乘积<ref>{{Cite journal|last=Zhang|first=Wei|last2=Wang|first2=Xiaogang|last3=Zhao|first3=Deli|last4=Tang|first4=Xiaoou|date=2012|editor-last=Fitzgibbon|editor-first=Andrew|editor2-last=Lazebnik|editor2-first=Svetlana|editor3-last=Perona|editor3-first=Pietro|editor4-last=Sato|editor4-first=Yoichi|editor5-last=Schmid|editor5-first=Cordelia|title=Graph Degree Linkage: Agglomerative Clustering on a Directed Graph|journal=Computer Vision – ECCV 2012|series=Lecture Notes in Computer Science|language=en|publisher=Springer Berlin Heidelberg|volume=7572|pages=428–441|doi=10.1007/978-3-642-33718-5_31|isbn=9783642337185|arxiv=1208.5092|bibcode=2012arXiv1208.5092Z}} See also: https://github.com/waynezhanghk/gacluster</ref> |
| − | + | * The increment of some cluster descriptor (i.e., a quantity defined for measuring the quality of a cluster) after merging two clusters.在合并了两个数据群之后,某个群的定义符号(即为度量一个簇的质量而定义的一个量)的增量。<ref>Zhang, et al. "Agglomerative clustering via maximum incremental path integral." Pattern Recognition (2013).</ref><ref>Zhao, and Tang. "Cyclizing clusters via zeta function of a graph."Advances in Neural Information Processing Systems. 2008.</ref><ref>Ma, et al. "Segmentation of multivariate mixed data via lossy data coding and compression." IEEE Transactions on Pattern Analysis and Machine Intelligence, 29(9) (2007): 1546-1562.</ref> | |
| − | |||
| − | + | ==讨论== | |
| − | + | 层次聚类具有明显的优势,它可以使用任何有效的距离度量。事实上,观测本身也并不是必需的,层次聚类所需要用的只是一个距离矩阵。 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Agglomerative clustering example 凝聚聚类实例== | == Agglomerative clustering example 凝聚聚类实例== | ||
| + | [[Image:Clusters.svg|frame|none|原始数据]] | ||
| + | 例如,假设要对这些数据进行聚类,将欧式距离作为度量。系统聚类[[树状图]]如下: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | [[Image:Hierarchical clustering simple diagram.svg|frame|none|传统展现法]] | ||
Cutting the tree at a given height will give a partitioning clustering at a selected precision. In this example, cutting after the second row (from the top) of the [[dendrogram]] will yield clusters {a} {b c} {d e} {f}. Cutting after the third row will yield clusters {a} {b c} {d e f}, which is a coarser clustering, with a smaller number but larger clusters. | Cutting the tree at a given height will give a partitioning clustering at a selected precision. In this example, cutting after the second row (from the top) of the [[dendrogram]] will yield clusters {a} {b c} {d e} {f}. Cutting after the third row will yield clusters {a} {b c} {d e f}, which is a coarser clustering, with a smaller number but larger clusters. | ||
| − | + | 在给定的高度切割树状图中,将以选定的精度提供分区聚类。在这个示例中,在树状图的第二行(从顶部开始)之后切割将产生类别{a} {b c} {d e} {f}。在第三行之后进行切割将产生类别{a} {b c} {d e f} ,这是一个较为粗略的但元素更繁多的类别,然而它的数量也较小。 | |
| − | |||
| − | |||
| − | |||
| 第507行: | 第153行: | ||
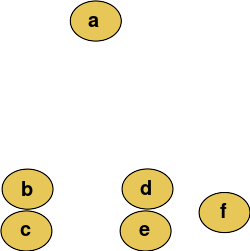
This method builds the hierarchy from the individual elements by progressively merging clusters. In our example, we have six elements {a} {b} {c} {d} {e} and {f}. The first step is to determine which elements to merge in a cluster. Usually, we want to take the two closest elements, according to the chosen distance. | This method builds the hierarchy from the individual elements by progressively merging clusters. In our example, we have six elements {a} {b} {c} {d} {e} and {f}. The first step is to determine which elements to merge in a cluster. Usually, we want to take the two closest elements, according to the chosen distance. | ||
| − | + | 此方法通过逐步合并集群,从单个元素构建层次结构。在我们的示例中,有六个元素{a} {b} {c} {d} {e}和{f}。第一步是确定在集群中合并哪些元素。通常,我们希望根据选定的距离获取两个最接近的元素。 | |
| − | |||
| − | 此方法通过逐步合并集群,从单个元素构建层次结构。在我们的示例中,有六个元素{ a }{ b }{ c }{ d }{ e }和{ f }。第一步是确定在集群中合并哪些元素。通常,我们希望根据选定的距离获取两个最接近的元素。 | ||
| 第515行: | 第159行: | ||
Optionally, one can also construct a [[distance matrix]] at this stage, where the number in the ''i''-th row ''j''-th column is the distance between the ''i''-th and ''j''-th elements. Then, as clustering progresses, rows and columns are merged as the clusters are merged and the distances updated. This is a common way to implement this type of clustering, and has the benefit of caching distances between clusters. A simple agglomerative clustering algorithm is described in the [[single-linkage clustering]] page; it can easily be adapted to different types of linkage (see below). | Optionally, one can also construct a [[distance matrix]] at this stage, where the number in the ''i''-th row ''j''-th column is the distance between the ''i''-th and ''j''-th elements. Then, as clustering progresses, rows and columns are merged as the clusters are merged and the distances updated. This is a common way to implement this type of clustering, and has the benefit of caching distances between clusters. A simple agglomerative clustering algorithm is described in the [[single-linkage clustering]] page; it can easily be adapted to different types of linkage (see below). | ||
| − | + | 还可以选择在这个阶段构造一个[[距离矩阵]],其中第i行第j列中的数字是 ''i''和''j'',即为两个元素之间的距离。然后,随着集群的进展,在合并集群和更新距离时合并行和列。这是实现此类集群的常用方法,并且具有缓存集群之间的距离的优点。在单链接聚类页面中描述了一个简单的凝聚聚类算法; 它适用于很多连接(见下文)。 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Suppose we have merged the two closest elements b and c, we now have the following clusters {a}, {b, c}, {d}, {e} and {f}, and want to merge them further. To do that, we need to take the distance between {a} and {b c}, and therefore define the distance between two clusters. | Suppose we have merged the two closest elements b and c, we now have the following clusters {a}, {b, c}, {d}, {e} and {f}, and want to merge them further. To do that, we need to take the distance between {a} and {b c}, and therefore define the distance between two clusters. | ||
| − | 假设我们已经合并了两个最接近的元素 b 和 | + | 假设我们已经合并了两个最接近的元素 ''b'' 和''c'',现在我们有以下集群{''a''}, {''b'', ''c''}, {''d''}, {''e''} 和{''f''} ,并希望进一步合并它们。为此,我们需要计算 {a} 和 {b c}之间的距离,从而定义两个集群之间的距离。 |
Usually the distance between two clusters <math>\mathcal{A}</math> and <math>\mathcal{B}</math> is one of the following: | Usually the distance between two clusters <math>\mathcal{A}</math> and <math>\mathcal{B}</math> is one of the following: | ||
| 第531行: | 第170行: | ||
Usually the distance between two clusters <math>\mathcal{A}</math> and <math>\mathcal{B}</math> is one of the following: | Usually the distance between two clusters <math>\mathcal{A}</math> and <math>\mathcal{B}</math> is one of the following: | ||
| − | + | 通常情况下,两个类别<math>\mathcal{A}</math>和 <math>\mathcal{B}</math>之间的距离是下列数字之一: | |
* The maximum distance between elements of each cluster (also called [[complete-linkage clustering]]): | * The maximum distance between elements of each cluster (also called [[complete-linkage clustering]]): | ||
| 第537行: | 第176行: | ||
::<math> \max \{\, d(x,y) : x \in \mathcal{A},\, y \in \mathcal{B}\,\}. </math> | ::<math> \max \{\, d(x,y) : x \in \mathcal{A},\, y \in \mathcal{B}\,\}. </math> | ||
| − | |||
| − | |||
| − | |||
* The minimum distance between elements of each cluster (also called [[single-linkage clustering]]): | * The minimum distance between elements of each cluster (also called [[single-linkage clustering]]): | ||
| 第545行: | 第181行: | ||
::<math> \min \{\, d(x,y) : x \in \mathcal{A},\, y \in \mathcal{B} \,\}. </math> | ::<math> \min \{\, d(x,y) : x \in \mathcal{A},\, y \in \mathcal{B} \,\}. </math> | ||
| − | |||
| − | |||
| − | |||
* The mean distance between elements of each cluster (also called average linkage clustering, used e.g. in [[UPGMA]]): | * The mean distance between elements of each cluster (also called average linkage clustering, used e.g. in [[UPGMA]]): | ||
| 第553行: | 第186行: | ||
::<math> {1 \over {|\mathcal{A}|\cdot|\mathcal{B}|}}\sum_{x \in \mathcal{A}}\sum_{ y \in \mathcal{B}} d(x,y). </math> | ::<math> {1 \over {|\mathcal{A}|\cdot|\mathcal{B}|}}\sum_{x \in \mathcal{A}}\sum_{ y \in \mathcal{B}} d(x,y). </math> | ||
| − | |||
| − | |||
| − | |||
* The sum of all intra-cluster variance. | * The sum of all intra-cluster variance. | ||
*所有集群内方差之和。 | *所有集群内方差之和。 | ||
| + | |||
* The increase in variance for the cluster being merged ([[Ward's method]]<ref name="wards method"/>) | * The increase in variance for the cluster being merged ([[Ward's method]]<ref name="wards method"/>) | ||
*合并的聚类的方差增加([[离差平方和法]]<ref name="离差平方和法"/>)。 | *合并的聚类的方差增加([[离差平方和法]]<ref name="离差平方和法"/>)。 | ||
| + | |||
* The probability that candidate clusters spawn from the same distribution function (V-linkage). | * The probability that candidate clusters spawn from the same distribution function (V-linkage). | ||
*候选集群从相同的分布函数中产生的概率(V—链路)。 | *候选集群从相同的分布函数中产生的概率(V—链路)。 | ||
| − | In case of tied minimum distances, a pair is randomly chosen, thus being able to generate several structurally different dendrograms. Alternatively, all tied pairs may be joined at the same time, generating a unique dendrogram. | + | In case of tied minimum distances, a pair is randomly chosen, thus being able to generate several structurally different dendrograms. Alternatively, all tied pairs may be joined at the same time, generating a unique dendrogram. |
| − | + | 在系结最小距离的情况下,一对元素是随机选择的,因此能够产生几个结构不同的树状图。或者,所有的绑定对可以在同一时间结合,产生一个唯一的树状图。<ref>{{cite journal | doi=10.1007/s00357-008-9004-x | last1=Fernández | first1=Alberto | last2=Gómez | first2=Sergio | title=Solving Non-uniqueness in Agglomerative Hierarchical Clustering Using Multidendrograms | journal=Journal of Classification | volume=25 | year=2008 | issue=1 | pages=43–65| arxiv=cs/0608049 }}</ref> | |
| − | |||
| − | One can always decide to stop clustering when there is a sufficiently small number of clusters (number criterion). Some linkages may also guarantee that agglomeration occurs at a greater distance between clusters than the previous agglomeration, and then one can stop clustering when the clusters are too far apart to be merged (distance criterion). However, this is not the case of, e.g., the centroid linkage where the so-called | + | One can always decide to stop clustering when there is a sufficiently small number of clusters (number criterion). Some linkages may also guarantee that agglomeration occurs at a greater distance between clusters than the previous agglomeration, and then one can stop clustering when the clusters are too far apart to be merged (distance criterion). However, this is not the case of, e.g., the centroid linkage where the so-called reversal (inversions, departures from ultrametricity) may occur. |
| − | + | 当有一个足够少的群集(数目标准)时,人们总是可以决定停止聚合。有些联系还可能保证集群之间的距离大于以前的集群,然后当集群之间的距离太远而无法合并时,就可以停止集群。然而,也有例外,如在质心链接的情况下,所谓的逆转(反转,偏离超节拍)就可能发生<ref>{{Cite book | last1= Legendre | first1 = P. | first2 = L. | last2=Legendre | title= Numerical Ecology | publisher=Elsevier Science BV | date=2003}}</ref>。 | |
| − | |||
== Divisive clustering分裂聚类 == | == Divisive clustering分裂聚类 == | ||
| − | |||
| − | |||
The basic principle of divisive clustering was published as the DIANA (DIvisive ANAlysis Clustering) algorithm. Initially, all data is in the same cluster, and the largest cluster is split until every object is separate. | The basic principle of divisive clustering was published as the DIANA (DIvisive ANAlysis Clustering) algorithm. Initially, all data is in the same cluster, and the largest cluster is split until every object is separate. | ||
| − | 分裂聚类的基本原理被公布为 DIANA (分裂分析聚类) | + | 分裂聚类的基本原理被公布为 DIANA (分裂分析聚类)算法<ref>Kaufman, L., & Roussew, P. J. (1990). Finding Groups in Data - An Introduction to Cluster Analysis. A Wiley-Science Publication John Wiley & Sons.</ref>。最初,所有数据都位于同一个集群中,然后最大的集群被拆分,依此类推,直到每个元素都是独立的。 |
Because there exist <math>O(2^n)</math> ways of splitting each cluster, heuristics are needed. DIANA chooses the object with the maximum average dissimilarity and then moves all objects to this cluster that are more similar to the new cluster than to the remainder. | Because there exist <math>O(2^n)</math> ways of splitting each cluster, heuristics are needed. DIANA chooses the object with the maximum average dissimilarity and then moves all objects to this cluster that are more similar to the new cluster than to the remainder. | ||
| − | + | 因为存在拆分每个集群的步骤是<math>O(2^n)</math>,所以需要探索试算法。DIANA 选择平均差异最大的对象,然后将所有与新集群相似的对象移动到这个集群中取代移动到其余的对象的方法。 | |
| − | |||
== Software 软件== | == Software 软件== | ||
| − | |||
| − | |||
| − | |||
=== Open source implementations 开源工具=== | === Open source implementations 开源工具=== | ||
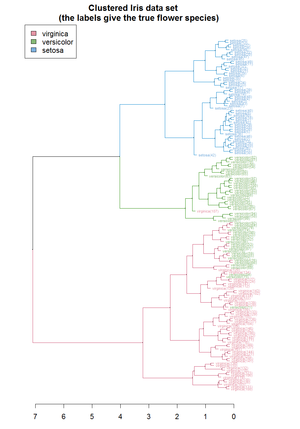
| − | + | [[File:Iris dendrogram.png|thumb|Hierarchical clustering [[dendrogram]] of the [[Iris flower data set|Iris dataset]] (using |R]]).层次聚类[[鸢尾花数据集]]的树状图(使用R语言) [https://cran.r-project.org/web/packages/dendextend/vignettes/Cluster_Analysis.html Source] ]] | |
| − | |||
| − | [[File:Iris dendrogram.png|thumb|Hierarchical clustering [[dendrogram]] of the [[Iris flower data set|Iris dataset]] (using | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
[[File:Orange-data-mining-hierarchical-clustering.png|thumb|Hierarchical clustering and interactive dendrogram visualization in [[Orange (software)|Orange data mining suite]].]] | [[File:Orange-data-mining-hierarchical-clustering.png|thumb|Hierarchical clustering and interactive dendrogram visualization in [[Orange (software)|Orange data mining suite]].]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| 第655行: | 第267行: | ||
*[[CrimeStat]]包括一个能够为地理位置提供图形输出的最近邻层次聚类算法。 | *[[CrimeStat]]包括一个能够为地理位置提供图形输出的最近邻层次聚类算法。 | ||
| − | == | + | == 参见 == |
{{Div col|colwidth=20em}} | {{Div col|colwidth=20em}} | ||
| 第693行: | 第305行: | ||
* [[Statistical distance]] | * [[Statistical distance]] | ||
[[统计距离]] | [[统计距离]] | ||
| − | * [[Persistent homology]] | + | * [[Persistent homology]] |
| − | [[持续同调]] | + | [[持续同调]] |
| − | == | + | == 参考文献== |
{{reflist|30em}} | {{reflist|30em}} | ||
| 第702行: | 第314行: | ||
| − | == | + | == 进一步阅读== |
* {{cite book |last1=Kaufman |first1=L. |last2=Rousseeuw |first2=P.J. |year=1990 |title=Finding Groups in Data: An Introduction to Cluster Analysis |edition=1 |isbn=0-471-87876-6 |publisher=John Wiley |location=New York |url-access=registration |url=https://archive.org/details/findinggroupsind00kauf }} | * {{cite book |last1=Kaufman |first1=L. |last2=Rousseeuw |first2=P.J. |year=1990 |title=Finding Groups in Data: An Introduction to Cluster Analysis |edition=1 |isbn=0-471-87876-6 |publisher=John Wiley |location=New York |url-access=registration |url=https://archive.org/details/findinggroupsind00kauf }} | ||
| 第710行: | 第322行: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[Category:网络分析]] | |
| − | [[Category: | + | [[Category:数据聚类算法]] |
2020年10月24日 (六) 23:52的版本
此词条暂由水流心不竞翻译,未经审校,带来阅读不便,请见谅。由CecileLi初步审校。翻译评级:B
在数据挖掘和统计学中, 层次聚类 Hierarchical clustering(也被称为“层次数据聚类或”“HCA”)是一种通过建立一个集群层次结构来聚类分析的方法。实现层次聚类的方法通常有两种:[1]
- 凝聚聚类 Agglomerative:这是一种“自上而下又自下而上/纵向”的方法:每个被观察数据从自己的簇类中开始,当一个观察组数据向上层移动时,成对的簇类集群被合并。
- 分裂聚类 Divisive: 这是一种“自上而下”的方法:所有的被观察数据都从一个簇类集群中开始,当一个簇类向下移动时,整个观察组数据群会递归地执行分割。
In general, the merges and splits are determined in a greedy manner. The results of hierarchical clustering引用错误:没有找到与</ref>对应的<ref>标签 通常在树状图中呈现。
层次凝聚聚类 Hierarchical agglomerative clustering(HAC)的标准算法的时间复杂度为[math]\displaystyle{ \mathcal{O}(n^3) }[/math] ,并且需要 [math]\displaystyle{ \mathcal{O}(n^2) }[/math] 占用内存,这使得它对于中等数据集来说效率太低了。然而,对于某些特殊情况,已知的最有效凝聚方法(复杂度 [math]\displaystyle{ \mathcal{O}(n^2) }[/math])是: SLINK 用于单连接[2] for single-linkage, CLINK用于完全连接[3]complete-linkage clustering。一般情况下的运行时可以缩减为 [math]\displaystyle{ \mathcal{O}(n^2 \log n) }[/math] ,代价是进一步增加内存需求。在多数情况下,这种方法的内存消耗太大,并不实用。
Except for the special case of single-linkage, none of the algorithms (except exhaustive search in [math]\displaystyle{ \mathcal{O}(2^n) }[/math]) can be guaranteed to find the optimum solution.
除了单连接的特殊情况外,所有算法(除了[math]\displaystyle{ \mathcal{O}(2^n) }[/math]数学中的穷举搜索)都不能保证找到最优解。
Divisive clustering with an exhaustive search is [math]\displaystyle{ \mathcal{O}(2^n) }[/math], but it is common to use faster heuristics to choose splits, such as k-means.
穷举搜索的分裂群集是 [math]\displaystyle{ \mathcal{O}(2^n) }[/math],但是通常使用运算速度更快的探索法来选择分裂,比如k-means。
簇异性 Cluster dissimilarity
In order to decide which clusters should be combined (for agglomerative), or where a cluster should be split (for divisive), a measure of dissimilarity between sets of observations is required. In most methods of hierarchical clustering, this is achieved by use of an appropriate metric (a measure of distance between pairs of observations), and a linkage criterion which specifies the dissimilarity of sets as a function of the pairwise distances of observations in the sets.
In order to decide which clusters should be combined (for agglomerative), or where a cluster should be split (for divisive), a measure of dissimilarity between sets of observations is required. In most methods of hierarchical clustering, this is achieved by use of an appropriate metric (a measure of distance between pairs of observations), and a linkage criterion which specifies the dissimilarity of sets as a function of the pairwise distances of observations in the sets.
为了决定哪些集群应该被组合起来(用于聚合) ,或者哪些集群应该被分离(用于分裂) ,需要在观察组之间进行不同程度的度量。在大多数层次聚类方法中,这是通过使用适当的度量(对观测值之间的距离度量)和联系准则来实现的,联系准则将集合的不同指定为观测值在集合中的成对距离的函数。
度量标准 Metric
更多信息请查看度量标准 Metric
The choice of an appropriate metric will influence the shape of the clusters, as some elements may be close to one another according to one distance and farther away according to another. For example, in a 2-dimensional space, the distance between the point (1,0) and the origin (0,0) is always 1 according to the usual norms, but the distance between the point (1,1) and the origin (0,0) can be 2 under Manhattan distance, [math]\displaystyle{ \scriptstyle\sqrt{2} }[/math] under Euclidean distance, or 1 under maximum distance.
度量方式的选择将影响数据簇类的形状,因为某些元素依据一个距离可能彼此接近,而依据另一个距离可能彼此远离。例如,在一个二维空间中,点(1,0)和原点(0,0)之间的距离通常是1,但是点(1,1)和原点(0,0)之间的距离在曼哈顿距离下可以是2,在欧几里得度量下可以是1,在最大距离下可以是1。
一些常用的 层次聚类 Hierarchical clustering指标如下:[4]
| 名字 | 公式 |
|---|---|
| 欧氏距离 Euclidean distance | [math]\displaystyle{ \|a-b \|_2 = \sqrt{\sum_i (a_i-b_i)^2} }[/math] |
| 平方欧氏距离 Squared Euclidean distance | [math]\displaystyle{ \|a-b \|_2^2 = \sum_i (a_i-b_i)^2 }[/math] |
| 曼哈顿距离 Manhattan distance | [math]\displaystyle{ \|a-b \|_1 = \sum_i |a_i-b_i| }[/math] |
| 最大距离 Maximum distance | [math]\displaystyle{ \|a-b \|_\infty = \max_i |a_i-b_i| }[/math] |
| 马氏距离 Mahalanobis distance | [math]\displaystyle{ \sqrt{(a-b)^{\top}S^{-1}(a-b)} }[/math] 其中S是协方差矩阵 |
For text or other non-numeric data, metrics such as the Hamming distance or Levenshtein distance are often used.
For text or other non-numeric data, metrics such as the Hamming distance or Levenshtein distance are often used.
对于文本文字或其他非数字数据,常常使用汉明距离 Hamming distance或编辑距离 Levenshtein distance等度量标准。
A review of cluster analysis in health psychology research found that the most common distance measure in published studies in that research area is the Euclidean distance or the squared Euclidean distance.
通过对数据聚类健康心理学研究的回顾发现,在该研究领域已发表的研究中,最常见的距离测量方法是欧几里得度量距离或欧几里得度量距离的平方。[citation needed]
Linkage criteria 连接准则
The linkage criterion determines the distance between sets of observations as a function of the pairwise distances between observations.
链接准则决定了观测值之间的距离,它是观测值之间成对距离的函数。
Some commonly used linkage criteria between two sets of observations A and B are:
| 名字 | 公式 |
|---|---|
| 最大或完全连接聚类 | [math]\displaystyle{ \max \, \{\, d(a,b) : a \in A,\, b \in B \,\} }[/math] |
| 最小或单连接聚类 | [math]\displaystyle{ \min \, \{\, d(a,b) : a \in A,\, b \in B \,\} }[/math] |
| 未加权平均链接聚类 Unweighted average linkage clustering (or UPGMA) | [math]\displaystyle{ \frac{1}{|A|\cdot|B|} \sum_{a \in A }\sum_{ b \in B} d(a,b) }[/math] |
| 加权平均数链接聚类 Weighted average linkage clustering (or WPGMA) | [math]\displaystyle{ d(i \cup j, k) = \frac{d(i, k) + d(j, k)}{2} |- | 质心链接集群 Centroid linkage clustering, or UPGMC | \lt math\gt \|c_s - c_t \| }[/math] where [math]\displaystyle{ c_s }[/math] and [math]\displaystyle{ c_t }[/math] 分别是 s类和 t类的中心. |
| 最小能量聚类Minimum energy clustering | [math]\displaystyle{ \frac {2}{nm}\sum_{i,j=1}^{n,m} \|a_i- b_j\|_2 - \frac {1}{n^2}\sum_{i,j=1}^{n} \|a_i-a_j\|_2 - \frac{1}{m^2}\sum_{i,j=1}^{m} \|b_i-b_j\|_2 }[/math] |
其中 d 是选定的度量单位。其他连接准则包括:
- The sum of all intra-cluster variance.所有簇内方差之和。
- The probability that candidate clusters spawn from the same distribution function (V-linkage).候选数据群从同一分布函数(V-连锁)中产生的概率。
- The product of in-degree and out-degree on a k-nearest-neighbour graph (graph degree linkage).k-最近邻图(图度连锁)上的入度与出度的乘积[8]
- The increment of some cluster descriptor (i.e., a quantity defined for measuring the quality of a cluster) after merging two clusters.在合并了两个数据群之后,某个群的定义符号(即为度量一个簇的质量而定义的一个量)的增量。[9][10][11]
讨论
层次聚类具有明显的优势,它可以使用任何有效的距离度量。事实上,观测本身也并不是必需的,层次聚类所需要用的只是一个距离矩阵。
Agglomerative clustering example 凝聚聚类实例
例如,假设要对这些数据进行聚类,将欧式距离作为度量。系统聚类树状图如下:
Cutting the tree at a given height will give a partitioning clustering at a selected precision. In this example, cutting after the second row (from the top) of the dendrogram will yield clusters {a} {b c} {d e} {f}. Cutting after the third row will yield clusters {a} {b c} {d e f}, which is a coarser clustering, with a smaller number but larger clusters. 在给定的高度切割树状图中,将以选定的精度提供分区聚类。在这个示例中,在树状图的第二行(从顶部开始)之后切割将产生类别{a} {b c} {d e} {f}。在第三行之后进行切割将产生类别{a} {b c} {d e f} ,这是一个较为粗略的但元素更繁多的类别,然而它的数量也较小。
This method builds the hierarchy from the individual elements by progressively merging clusters. In our example, we have six elements {a} {b} {c} {d} {e} and {f}. The first step is to determine which elements to merge in a cluster. Usually, we want to take the two closest elements, according to the chosen distance.
此方法通过逐步合并集群,从单个元素构建层次结构。在我们的示例中,有六个元素{a} {b} {c} {d} {e}和{f}。第一步是确定在集群中合并哪些元素。通常,我们希望根据选定的距离获取两个最接近的元素。
Optionally, one can also construct a distance matrix at this stage, where the number in the i-th row j-th column is the distance between the i-th and j-th elements. Then, as clustering progresses, rows and columns are merged as the clusters are merged and the distances updated. This is a common way to implement this type of clustering, and has the benefit of caching distances between clusters. A simple agglomerative clustering algorithm is described in the single-linkage clustering page; it can easily be adapted to different types of linkage (see below).
还可以选择在这个阶段构造一个距离矩阵,其中第i行第j列中的数字是 i和j,即为两个元素之间的距离。然后,随着集群的进展,在合并集群和更新距离时合并行和列。这是实现此类集群的常用方法,并且具有缓存集群之间的距离的优点。在单链接聚类页面中描述了一个简单的凝聚聚类算法; 它适用于很多连接(见下文)。
Suppose we have merged the two closest elements b and c, we now have the following clusters {a}, {b, c}, {d}, {e} and {f}, and want to merge them further. To do that, we need to take the distance between {a} and {b c}, and therefore define the distance between two clusters.
假设我们已经合并了两个最接近的元素 b 和c,现在我们有以下集群{a}, {b, c}, {d}, {e} 和{f} ,并希望进一步合并它们。为此,我们需要计算 {a} 和 {b c}之间的距离,从而定义两个集群之间的距离。
Usually the distance between two clusters [math]\displaystyle{ \mathcal{A} }[/math] and [math]\displaystyle{ \mathcal{B} }[/math] is one of the following:
Usually the distance between two clusters [math]\displaystyle{ \mathcal{A} }[/math] and [math]\displaystyle{ \mathcal{B} }[/math] is one of the following:
通常情况下,两个类别[math]\displaystyle{ \mathcal{A} }[/math]和 [math]\displaystyle{ \mathcal{B} }[/math]之间的距离是下列数字之一:
- The maximum distance between elements of each cluster (also called complete-linkage clustering):
- 每个集群元素之间的最大距离(又名完全链路集)
- [math]\displaystyle{ \max \{\, d(x,y) : x \in \mathcal{A},\, y \in \mathcal{B}\,\}. }[/math]
- The minimum distance between elements of each cluster (also called single-linkage clustering):
- 每个集群的元素之间的最小距离(也称为单个链路集):
- [math]\displaystyle{ \min \{\, d(x,y) : x \in \mathcal{A},\, y \in \mathcal{B} \,\}. }[/math]
- The mean distance between elements of each cluster (also called average linkage clustering, used e.g. in UPGMA):
- 每个簇元素之间的平均距离(也称为平均链路集):
- [math]\displaystyle{ {1 \over {|\mathcal{A}|\cdot|\mathcal{B}|}}\sum_{x \in \mathcal{A}}\sum_{ y \in \mathcal{B}} d(x,y). }[/math]
- The sum of all intra-cluster variance.
- 所有集群内方差之和。
- The increase in variance for the cluster being merged (Ward's method[7])
- 合并的聚类的方差增加(离差平方和法[12])。
- The probability that candidate clusters spawn from the same distribution function (V-linkage).
- 候选集群从相同的分布函数中产生的概率(V—链路)。
In case of tied minimum distances, a pair is randomly chosen, thus being able to generate several structurally different dendrograms. Alternatively, all tied pairs may be joined at the same time, generating a unique dendrogram.
在系结最小距离的情况下,一对元素是随机选择的,因此能够产生几个结构不同的树状图。或者,所有的绑定对可以在同一时间结合,产生一个唯一的树状图。[13]
One can always decide to stop clustering when there is a sufficiently small number of clusters (number criterion). Some linkages may also guarantee that agglomeration occurs at a greater distance between clusters than the previous agglomeration, and then one can stop clustering when the clusters are too far apart to be merged (distance criterion). However, this is not the case of, e.g., the centroid linkage where the so-called reversal (inversions, departures from ultrametricity) may occur.
当有一个足够少的群集(数目标准)时,人们总是可以决定停止聚合。有些联系还可能保证集群之间的距离大于以前的集群,然后当集群之间的距离太远而无法合并时,就可以停止集群。然而,也有例外,如在质心链接的情况下,所谓的逆转(反转,偏离超节拍)就可能发生[14]。
Divisive clustering分裂聚类
The basic principle of divisive clustering was published as the DIANA (DIvisive ANAlysis Clustering) algorithm. Initially, all data is in the same cluster, and the largest cluster is split until every object is separate.
分裂聚类的基本原理被公布为 DIANA (分裂分析聚类)算法[15]。最初,所有数据都位于同一个集群中,然后最大的集群被拆分,依此类推,直到每个元素都是独立的。
Because there exist [math]\displaystyle{ O(2^n) }[/math] ways of splitting each cluster, heuristics are needed. DIANA chooses the object with the maximum average dissimilarity and then moves all objects to this cluster that are more similar to the new cluster than to the remainder.
因为存在拆分每个集群的步骤是[math]\displaystyle{ O(2^n) }[/math],所以需要探索试算法。DIANA 选择平均差异最大的对象,然后将所有与新集群相似的对象移动到这个集群中取代移动到其余的对象的方法。
Software 软件
Open source implementations 开源工具
).层次聚类鸢尾花数据集的树状图(使用R语言) Source ]]

- ALGLIB implements several hierarchical clustering algorithms (single-link, complete-link, Ward) in C++ and C# with O(n²) memory and O(n³) run time.
- ALGLIB在C++ 和 C# 上以O(n²) 的内存和O(n³)的运行时间实现了几个层次聚类算法(单链接,完整链接,均值)。
- ELKI includes multiple hierarchical clustering algorithms, various linkage strategies and also includes the efficient SLINK,[2] CLINK[3] and Anderberg algorithms, flexible cluster extraction from dendrograms and various other cluster analysis algorithms.
- ELKI包括多种层次聚类算法,各种链接策略,同时包括高效运行,[2] CLINK[3] 安德伯格算法,从树状图和其他各种聚类分析算法中进行灵活的聚类提取。
- Octave, the GNU analog to MATLAB implements hierarchical clustering in function "linkage".
- Octave,与MATLAB类似的GNU在“联动”功能中实现了分层聚类。
- Orange, a data mining software suite, includes hierarchical clustering with interactive dendrogram visualisation.
- Orange,一个数据挖掘软件套件,包括层次聚类和交互式可视化树形图。
- R has many packages that provide functions for hierarchical clustering.
- R 有许多提供分层聚类功能的工具包。
- SciPy implements hierarchical clustering in Python, including the efficient SLINK algorithm.
- SciPy在python中实现分层聚类,包括高效的slink算法。
- scikit-learn also implements hierarchical clustering in Python.
- scikit-learn还实现了Python中的层次聚类。
- Weka includes hierarchical cluster analysis.
- Weka 包括层次聚类分析。
Commercial implementations 商业实践
- MATLAB includes hierarchical cluster analysis.
- MATLAB 包括层次聚类分析。
- SAS includes hierarchical cluster analysis in PROC CLUSTER.
- SAS包括在群聚程序中进行层次聚类分析。
- Mathematica includes a Hierarchical Clustering Package.
- Mathematica 包括一组层次聚类分析工具包。
- NCSS includes hierarchical cluster analysis.
- NCSS 包括层次聚类分析。
- SPSS includes hierarchical cluster analysis.
- SPSS包括层次聚类分析。
- Qlucore Omics Explorer includes hierarchical cluster analysis.
- Qlucore包括层次聚类分析的Omits 资源管理器。
- Stata includes hierarchical cluster analysis.
- Stata 包括层次聚类分析。
- CrimeStat includes a nearest neighbor hierarchical cluster algorithm with a graphical output for a Geographic Information System.
- CrimeStat包括一个能够为地理位置提供图形输出的最近邻层次聚类算法。
参见
参考文献
- ↑ Rokach, Lior, and Oded Maimon. "Clustering methods." Data mining and knowledge discovery handbook. Springer US, 2005. 321-352.
- ↑ 2.0 2.1 2.2 R. Sibson (1973). "SLINK: an optimally efficient algorithm for the single-link cluster method" (PDF). The Computer Journal. British Computer Society. 16 (1): 30–34. doi:10.1093/comjnl/16.1.30.
- ↑ 3.0 3.1 3.2 D. Defays (1977). "An efficient algorithm for a complete-link method". The Computer Journal. British Computer Society. 20 (4): 364–366. doi:10.1093/comjnl/20.4.364.
- ↑ "The DISTANCE Procedure: Proximity Measures". SAS/STAT 9.2 Users Guide. SAS Institute. Retrieved 2009-04-26.
- ↑ "The CLUSTER Procedure: Clustering Methods". SAS/STAT 9.2 Users Guide. SAS Institute. Retrieved 2009-04-26.
- ↑ Székely, G. J.; Rizzo, M. L. (2005). "Hierarchical clustering via Joint Between-Within Distances: Extending Ward's Minimum Variance Method". Journal of Classification. 22 (2): 151–183. doi:10.1007/s00357-005-0012-9.
- ↑ 7.0 7.1 Ward, Joe H. (1963). "Hierarchical Grouping to Optimize an Objective Function". Journal of the American Statistical Association. 58 (301): 236–244. doi:10.2307/2282967.
- ↑ Zhang, Wei; Wang, Xiaogang; Zhao, Deli; Tang, Xiaoou (2012). Fitzgibbon, Andrew; Lazebnik, Svetlana; Perona, Pietro; Sato, Yoichi; Schmid, Cordelia (eds.). "Graph Degree Linkage: Agglomerative Clustering on a Directed Graph". Computer Vision – ECCV 2012. Lecture Notes in Computer Science (in English). Springer Berlin Heidelberg. 7572: 428–441. arXiv:1208.5092. Bibcode:2012arXiv1208.5092Z. doi:10.1007/978-3-642-33718-5_31. ISBN 9783642337185. See also: https://github.com/waynezhanghk/gacluster
- ↑ Zhang, et al. "Agglomerative clustering via maximum incremental path integral." Pattern Recognition (2013).
- ↑ Zhao, and Tang. "Cyclizing clusters via zeta function of a graph."Advances in Neural Information Processing Systems. 2008.
- ↑ Ma, et al. "Segmentation of multivariate mixed data via lossy data coding and compression." IEEE Transactions on Pattern Analysis and Machine Intelligence, 29(9) (2007): 1546-1562.
- ↑ 引用错误:无效
<ref>标签;未给name属性为离差平方和法的引用提供文字 - ↑ Fernández, Alberto; Gómez, Sergio (2008). "Solving Non-uniqueness in Agglomerative Hierarchical Clustering Using Multidendrograms". Journal of Classification. 25 (1): 43–65. arXiv:cs/0608049. doi:10.1007/s00357-008-9004-x.
- ↑ Legendre, P.; Legendre, L. (2003). Numerical Ecology. Elsevier Science BV.
- ↑ Kaufman, L., & Roussew, P. J. (1990). Finding Groups in Data - An Introduction to Cluster Analysis. A Wiley-Science Publication John Wiley & Sons.
进一步阅读
- Kaufman, L.; Rousseeuw, P.J. (1990). Finding Groups in Data: An Introduction to Cluster Analysis (1 ed.). New York: John Wiley. ISBN 0-471-87876-6. https://archive.org/details/findinggroupsind00kauf.
- Hastie, Trevor; Tibshirani, Robert; Friedman, Jerome (2009). "14.3.12 Hierarchical clustering". The Elements of Statistical Learning (2nd ed.). New York: Springer. pp. 520–528. ISBN 978-0-387-84857-0. Archived from the original on 2009-11-10. http://www-stat.stanford.edu/~tibs/ElemStatLearn/. Retrieved 2009-10-20.