“条件熵”的版本间的差异
(Moved page from wikipedia:en:Conditional entropy (history)) |
小 (Moved page from wikipedia:en:Conditional entropy (history)) |
||
| 第1行: | 第1行: | ||
| − | 此词条暂由彩云小译翻译,未经人工整理和审校,带来阅读不便,请见谅。 | + | 此词条暂由彩云小译翻译,未经人工整理和审校,带来阅读不便,请见谅。 |
| − | |||
| + | {{Short description|Measure of relative information in probability theory}} | ||
{{Information theory}} | {{Information theory}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| 第15行: | 第11行: | ||
[[Venn diagram showing additive and subtractive relationships various information measures associated with correlated variables <math>X</math> and <math>Y</math>. The area contained by both circles is the joint entropy <math>\Eta(X,Y)</math>. The circle on the left (red and violet) is the individual entropy <math>\Eta(X)</math>, with the red being the conditional entropy <math>\Eta(X|Y)</math>. The circle on the right (blue and violet) is <math>\Eta(Y)</math>, with the blue being <math>\Eta(Y|X)</math>. The violet is the mutual information <math>\operatorname{I}(X;Y)</math>.]] | [[Venn diagram showing additive and subtractive relationships various information measures associated with correlated variables <math>X</math> and <math>Y</math>. The area contained by both circles is the joint entropy <math>\Eta(X,Y)</math>. The circle on the left (red and violet) is the individual entropy <math>\Eta(X)</math>, with the red being the conditional entropy <math>\Eta(X|Y)</math>. The circle on the right (blue and violet) is <math>\Eta(Y)</math>, with the blue being <math>\Eta(Y|X)</math>. The violet is the mutual information <math>\operatorname{I}(X;Y)</math>.]] | ||
| − | + | 文恩图显示了相加和相减的关系,各种信息测量与相关变量相关。两个圆圈所包含的区域是联合熵。左边的圆圈(红色和紫色)代表个体熵。左边的圆圈代表个体熵。右边的圆圈代表个体熵。右边的圆圈代表个体熵。右边的圆圈代表个体熵。右边的圆圈代表个体熵。右边的圆圈代表个体熵。右边的圆圈代表个体熵。右边的圆圈代表个体熵。右边的圆圈代表个体熵。右边的圆圈代表个体。右边的圆圈(蓝色和紫色)是 < math > Eta (y) </math > ,蓝色的是 < math > Eta (y | x) </math > 。紫色是共同的信息[ math > 操作者名称{ i }(x; y) </math > ] | |
| + | In [[information theory]], the '''conditional entropy''' quantifies the amount of information needed to describe the outcome of a [[random variable]] <math>Y</math> given that the value of another random variable <math>X</math> is known. Here, information is measured in [[Shannon (unit)|shannon]]s, [[Nat (unit)|nat]]s, or [[Hartley (unit)|hartley]]s. The ''entropy of <math>Y</math> conditioned on <math>X</math>'' is written as <math>\Eta(Y|X)</math>. | ||
| + | In information theory, the conditional entropy quantifies the amount of information needed to describe the outcome of a random variable <math>Y</math> given that the value of another random variable <math>X</math> is known. Here, information is measured in shannons, nats, or hartleys. The entropy of <math>Y</math> conditioned on <math>X</math> is written as <math>\Eta(Y|X)</math>. | ||
| − | + | 在信息论中,如果另一个随机变量的值是已知的,那么条件熵就会量化描述一个随机变量的结果所需的信息量。在这里,信息是用夏农、纳特斯或哈特利来衡量的。“数学”的熵取决于“数学” ,“ x”表示“数学” ,“埃塔”表示“数学”。 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Definition == | == Definition == | ||
| − | |||
| − | |||
The conditional entropy of <math>Y</math> given <math>X</math> is defined as | The conditional entropy of <math>Y</math> given <math>X</math> is defined as | ||
| 第41行: | 第29行: | ||
The conditional entropy of <math>Y</math> given <math>X</math> is defined as | The conditional entropy of <math>Y</math> given <math>X</math> is defined as | ||
| − | + | 给定的 x 条件熵被定义为 | |
| − | |||
| − | |||
| 第57行: | 第43行: | ||
|indent = | |indent = | ||
| − | + | 2012年10月22日 | |
|title= | |title= | ||
| 第63行: | 第49行: | ||
|title= | |title= | ||
| − | + | 2012年10月11日 | |
|equation = {{NumBlk||<math>\Eta(Y|X)\ = -\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log \frac {p(x,y)} {p(x)}</math>|{{EquationRef|Eq.1}}}} | |equation = {{NumBlk||<math>\Eta(Y|X)\ = -\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log \frac {p(x,y)} {p(x)}</math>|{{EquationRef|Eq.1}}}} | ||
| 第69行: | 第55行: | ||
|equation = }} | |equation = }} | ||
| − | + | | equation = } | |
|cellpadding= 6 | |cellpadding= 6 | ||
| 第75行: | 第61行: | ||
|cellpadding= 6 | |cellpadding= 6 | ||
| − | + | 6 | |
|border | |border | ||
| 第93行: | 第79行: | ||
|background colour=#F5FFFA}} | |background colour=#F5FFFA}} | ||
| − | 5 / fffa } | + | 5/fffa }} |
| − | |||
| − | |||
| 第103行: | 第87行: | ||
where <math>\mathcal X</math> and <math>\mathcal Y</math> denote the support sets of <math>X</math> and <math>Y</math>. | where <math>\mathcal X</math> and <math>\mathcal Y</math> denote the support sets of <math>X</math> and <math>Y</math>. | ||
| − | + | 这里 < math > 数学 x </math > 和 < math > > 数学 y </math > 表示 < math > x </math > 和 < math > y </math > 的支持集。 | |
| − | |||
| − | |||
| 第111行: | 第93行: | ||
''Note:'' It is conventioned that the expressions <math>0 \log 0</math> and <math>0 \log c/0</math> for fixed <math>c > 0</math> should be treated as being equal to zero. This is because <math>\lim_{\theta\to0^+} \theta\, \log \,c/\theta = 0</math> and <math>\lim_{\theta\to0^+} \theta\, \log \theta = 0</math><ref>{{Cite web|url=http://www.inference.org.uk/mackay/itprnn/book.html|title=David MacKay: Information Theory, Pattern Recognition and Neural Networks: The Book|website=www.inference.org.uk|access-date=2019-10-25}}</ref> <!-- because p(x,y) could still equal 0 even if p(x) != 0 and p(y) != 0. What about p(x,y)=p(x)=0? --> | ''Note:'' It is conventioned that the expressions <math>0 \log 0</math> and <math>0 \log c/0</math> for fixed <math>c > 0</math> should be treated as being equal to zero. This is because <math>\lim_{\theta\to0^+} \theta\, \log \,c/\theta = 0</math> and <math>\lim_{\theta\to0^+} \theta\, \log \theta = 0</math><ref>{{Cite web|url=http://www.inference.org.uk/mackay/itprnn/book.html|title=David MacKay: Information Theory, Pattern Recognition and Neural Networks: The Book|website=www.inference.org.uk|access-date=2019-10-25}}</ref> <!-- because p(x,y) could still equal 0 even if p(x) != 0 and p(y) != 0. What about p(x,y)=p(x)=0? --> | ||
| − | Note: It is conventioned that the expressions <math>0 \log 0</math> and <math>0 \log c/0</math> for fixed <math>c > 0</math> should be treated as being equal to zero. This is because <math>\lim_{\theta\to0^+} \theta\, \log \,c/\theta = 0</math> and <math>\lim_{\theta\to0^+} \theta\, \log \theta = 0</math> | + | Note: It is conventioned that the expressions <math>0 \log 0</math> and <math>0 \log c/0</math> for fixed <math>c > 0</math> should be treated as being equal to zero. This is because <math>\lim_{\theta\to0^+} \theta\, \log \,c/\theta = 0</math> and <math>\lim_{\theta\to0^+} \theta\, \log \theta = 0</math> |
| − | |||
| − | |||
| − | |||
| + | 注意: 常规的表达式 < math > 0 log 0 </math > 和 < math > 0 log c/0 </math > 对于 fixed < math > c > 0 </math > 应该被视为等于零。这是因为 < math > lim { theta to0 ^ + } theta,log,c/theta = 0 </math > 和 < math > lim { theta to0 ^ + } theta,log theta = 0 </math > | ||
| 第121行: | 第101行: | ||
Intuitive explanation of the definition : | Intuitive explanation of the definition : | ||
| − | + | The chain rule follows from the above definition of conditional entropy: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | 链式规则遵循了上述条件熵的定义: | ||
| + | According to the definition, <math>\displaystyle H( Y|X) =\mathbb{E}( \ f( X,Y) \ )</math> where <math>\displaystyle f:( x,y) \ \rightarrow -\log( \ p( y|x) \ ) .</math> <math>\displaystyle f</math> associates to <math>\displaystyle ( x,y)</math> the information content of <math>\displaystyle ( Y=y)</math> given <math>\displaystyle (X=x)</math>, which is the amount of information needed to describe the event <math>\displaystyle (Y=y)</math> given <math>(X=x)</math>. According to the law of large numbers, <math>\displaystyle H(Y|X)</math> is the arithmetic mean of a large number of independent realizations of <math>\displaystyle f(X,Y)</math>. | ||
| + | <math>\begin{align} | ||
| + | 1.1.1.2.2.2.2.2.2.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.4.3.3.3.3.3.3.3.3.3.3.3.4.3.3.3.3.3.3.3.3.3 | ||
== Motivation == | == Motivation == | ||
| − | = | + | \Eta(Y|X) &= \sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log \left(\frac{p(x)}{p(x,y)} \right) \\[4pt] |
| − | + | Eta (y | x) & = sum _ { x in mathcal x,y in mathcal y } p (x,y) log left (frac { p (x)}{ p (x,y)} right)[4 pt ] | |
Let <math>\Eta(Y|X=x)</math> be the [[Shannon Entropy|entropy]] of the discrete random variable <math>Y</math> conditioned on the discrete random variable <math>X</math> taking a certain value <math>x</math>. Denote the support sets of <math>X</math> and <math>Y</math> by <math>\mathcal X</math> and <math>\mathcal Y</math>. Let <math>Y</math> have [[probability mass function]] <math>p_Y{(y)}</math>. The unconditional entropy of <math>Y</math> is calculated as <math>\Eta(Y) := \mathbb{E}[\operatorname{I}(Y)]</math>, i.e. | Let <math>\Eta(Y|X=x)</math> be the [[Shannon Entropy|entropy]] of the discrete random variable <math>Y</math> conditioned on the discrete random variable <math>X</math> taking a certain value <math>x</math>. Denote the support sets of <math>X</math> and <math>Y</math> by <math>\mathcal X</math> and <math>\mathcal Y</math>. Let <math>Y</math> have [[probability mass function]] <math>p_Y{(y)}</math>. The unconditional entropy of <math>Y</math> is calculated as <math>\Eta(Y) := \mathbb{E}[\operatorname{I}(Y)]</math>, i.e. | ||
| − | + | &= \sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)(\log (p(x))-\log (p(x,y))) \\[4pt] | |
| − | + | & = sum _ { x in mathcal x,y in mathcal y } p (x,y)(log (p (x))-log (p (x,y)))[4 pt ] | |
| + | &= -\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log (p(x,y)) + \sum_{x\in\mathcal X, y\in\mathcal Y}{p(x,y)\log(p(x))} \\[4pt] | ||
| + | & =-sum _ { x in mathcal x,y in mathcal y } p (x,y) log (p (x,y)) + sum _ { x in mathcal x,y in mathcal y }{ p (x,y) log (p (x))}[4 pt ] | ||
:<math>\Eta(Y) = \sum_{y\in\mathcal Y} {\mathrm{Pr}(Y=y)\,\mathrm{I}(y)} | :<math>\Eta(Y) = \sum_{y\in\mathcal Y} {\mathrm{Pr}(Y=y)\,\mathrm{I}(y)} | ||
| − | + | & = \Eta(X,Y) + \sum_{x \in \mathcal X} p(x)\log (p(x) ) \\[4pt] | |
| − | + | & = Eta (x,y) + sum _ { x in mathcal x } p (x) log (p (x))[4 pt ] | |
= -\sum_{y\in\mathcal Y} {p_Y(y) \log_2{p_Y(y)}},</math> | = -\sum_{y\in\mathcal Y} {p_Y(y) \log_2{p_Y(y)}},</math> | ||
| − | = | + | & = \Eta(X,Y) - \Eta(X). |
| − | + | & = Eta (x,y)-Eta (x). | |
| + | \end{align}</math> | ||
| + | 结束{ align } </math > | ||
where <math>\operatorname{I}(y_i)</math> is the [[information content]] of the [[Outcome (probability)|outcome]] of <math>Y</math> taking the value <math>y_i</math>. The entropy of <math>Y</math> conditioned on <math>X</math> taking the value <math>x</math> is defined analogously by [[conditional expectation]]: | where <math>\operatorname{I}(y_i)</math> is the [[information content]] of the [[Outcome (probability)|outcome]] of <math>Y</math> taking the value <math>y_i</math>. The entropy of <math>Y</math> conditioned on <math>X</math> taking the value <math>x</math> is defined analogously by [[conditional expectation]]: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | In general, a chain rule for multiple random variables holds: | ||
| + | 一般来说,多个随机变量的链式规则适用于: | ||
:<math>\Eta(Y|X=x) | :<math>\Eta(Y|X=x) | ||
| − | + | = -\sum_{y\in\mathcal Y} {\Pr(Y = y|X=x) \log_2{\Pr(Y = y|X=x)}}.</math> | |
| − | ( | + | <math> \Eta(X_1,X_2,\ldots,X_n) = |
| − | + | < math > Eta (x1,x2,ldots,xn) = | |
| − | + | Note that <math>\Eta(Y|X)</math> is the result of averaging <math>\Eta(Y|X=x)</math> over all possible values <math>x</math> that <math>X</math> may take. Also, if the above sum is taken over a sample <math>y_1, \dots, y_n</math>, the expected value <math>E_X[ \Eta(y_1, \dots, y_n \mid X = x)]</math> is known in some domains as '''equivocation'''.<ref>{{cite journal|author1=Hellman, M.|author2=Raviv, J.|year=1970|title=Probability of error, equivocation, and the Chernoff bound|journal=IEEE Transactions on Information Theory|volume=16|issue=4|pp=368-372}}</ref> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | <math>\Eta(Y|X)</math> is the result of averaging <math>\Eta(Y|X=x)</math> over all possible values <math>x</math> that <math>X</math> may take. | ||
| − | |||
| − | <math>\ | ||
| − | |||
| − | |||
| + | \sum_{i=1}^n \Eta(X_i | X_1, \ldots, X_{i-1}) </math> | ||
| + | Sum { i = 1} ^ n Eta (x _ i | x _ 1,ldots,x _ { i-1}) </math > | ||
| 第209行: | 第175行: | ||
Given [[Discrete random variable|discrete random variables]] <math>X</math> with image <math>\mathcal X</math> and <math>Y</math> with image <math>\mathcal Y</math>, the conditional entropy of <math>Y</math> given <math>X</math> is defined as the weighted sum of <math>\Eta(Y|X=x)</math> for each possible value of <math>x</math>, using <math>p(x)</math> as the weights:<ref name=cover1991>{{cite book|isbn=0-471-06259-6|year=1991|authorlink1=Thomas M. Cover|author1=T. Cover|author2=J. Thomas|title=Elements of Information Theory|url=https://archive.org/details/elementsofinform0000cove|url-access=registration}}</ref>{{rp|15}} | Given [[Discrete random variable|discrete random variables]] <math>X</math> with image <math>\mathcal X</math> and <math>Y</math> with image <math>\mathcal Y</math>, the conditional entropy of <math>Y</math> given <math>X</math> is defined as the weighted sum of <math>\Eta(Y|X=x)</math> for each possible value of <math>x</math>, using <math>p(x)</math> as the weights:<ref name=cover1991>{{cite book|isbn=0-471-06259-6|year=1991|authorlink1=Thomas M. Cover|author1=T. Cover|author2=J. Thomas|title=Elements of Information Theory|url=https://archive.org/details/elementsofinform0000cove|url-access=registration}}</ref>{{rp|15}} | ||
| − | + | It has a similar form to chain rule in probability theory, except that addition instead of multiplication is used. | |
| − | |||
| − | |||
| − | |||
| + | 除了用加法代替乘法之外,它的形式与概率论的链式法则相似。 | ||
:<math> | :<math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
\begin{align} | \begin{align} | ||
| − | + | Bayes' rule for conditional entropy states | |
| − | + | 条件熵的贝叶斯规则 | |
\Eta(Y|X)\ &\equiv \sum_{x\in\mathcal X}\,p(x)\,\Eta(Y|X=x)\\ | \Eta(Y|X)\ &\equiv \sum_{x\in\mathcal X}\,p(x)\,\Eta(Y|X=x)\\ | ||
| − | \Eta(Y|X) | + | <math>\Eta(Y|X) \,=\, \Eta(X|Y) - \Eta(X) + \Eta(Y).</math> |
| − | |||
| − | |||
| − | + | [数学] Eta (y | x) ,= ,Eta (x | y)-Eta (x) + Eta (y) | |
& =-\sum_{x\in\mathcal X} p(x)\sum_{y\in\mathcal Y}\,p(y|x)\,\log\, p(y|x)\\ | & =-\sum_{x\in\mathcal X} p(x)\sum_{y\in\mathcal Y}\,p(y|x)\,\log\, p(y|x)\\ | ||
| − | |||
| − | |||
& =-\sum_{x\in\mathcal X}\sum_{y\in\mathcal Y}\,p(x,y)\,\log\,p(y|x)\\ | & =-\sum_{x\in\mathcal X}\sum_{y\in\mathcal Y}\,p(x,y)\,\log\,p(y|x)\\ | ||
| − | + | Proof. <math>\Eta(Y|X) = \Eta(X,Y) - \Eta(X)</math> and <math>\Eta(X|Y) = \Eta(Y,X) - \Eta(Y)</math>. Symmetry entails <math>\Eta(X,Y) = \Eta(Y,X)</math>. Subtracting the two equations implies Bayes' rule. | |
| − | |||
| − | |||
| − | + | 证据。Eta (y | x) = Eta (x,y)-Eta (x) | math > Eta (x | y) = Eta (y,x)-Eta (y).对称意味着 Eta (x,y) = Eta (y,x)。减去这两个方程就得到了贝叶斯定律。 | |
& =-\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log\,p(y|x)\\ | & =-\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log\,p(y|x)\\ | ||
| − | |||
| − | |||
& =-\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log \frac {p(x,y)} {p(x)}. \\ | & =-\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log \frac {p(x,y)} {p(x)}. \\ | ||
| − | + | If <math>Y</math> is conditionally independent of <math>Z</math> given <math>X</math> we have: | |
| − | + | 如果[数学] y </math > 是条件独立于[数学] z </math > 给定 < 数学 > x </math > 我们有: | |
| − | |||
| − | |||
& = \sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log \frac {p(x)} {p(x,y)}. \\ | & = \sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log \frac {p(x)} {p(x,y)}. \\ | ||
| − | |||
| − | |||
\end{align} | \end{align} | ||
| − | \ | + | <math>\Eta(Y|X,Z) \,=\, \Eta(Y|X).</math> |
| − | + | [ math ] Eta (y | x,z) ,= ,Eta (y | x) | |
</math> | </math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| 第283行: | 第225行: | ||
<!-- This paragraph is incorrect; the last line is not the KL divergence between any two distributions, since p(x) is [in general] not a valid distribution over the domains of X and Y. The last formula above is the [[Kullback-Leibler divergence]], also known as relative entropy. Relative entropy is always positive, and vanishes if and only if <math>p(x,y) = p(x)</math>. This is when knowing <math>x</math> tells us everything about <math>y</math>. ADDED: Could this comment be out of date since the KL divergence is not mentioned above? November 2014 --> | <!-- This paragraph is incorrect; the last line is not the KL divergence between any two distributions, since p(x) is [in general] not a valid distribution over the domains of X and Y. The last formula above is the [[Kullback-Leibler divergence]], also known as relative entropy. Relative entropy is always positive, and vanishes if and only if <math>p(x,y) = p(x)</math>. This is when knowing <math>x</math> tells us everything about <math>y</math>. ADDED: Could this comment be out of date since the KL divergence is not mentioned above? November 2014 --> | ||
| − | + | For any <math>X</math> and <math>Y</math>: | |
| − | < | + | 对于任意的 < math > x </math > 和 < math > > y </math > : |
| + | <math display="block">\begin{align} | ||
| + | (数学显示 = “ block” > begin { align }) | ||
==Properties== | ==Properties== | ||
| − | + | \Eta(Y|X) &\le \Eta(Y) \, \\ | |
| − | + | 埃塔(y | x)及埃塔(y) , | |
===Conditional entropy equals zero=== | ===Conditional entropy equals zero=== | ||
| − | = | + | \Eta(X,Y) &= \Eta(X|Y) + \Eta(Y|X) + \operatorname{I}(X;Y),\qquad \\ |
| − | + | eta (x,y) & = Eta (x | y) + Eta (y | x) + 操作数名{ i }(x; y) ,qquad | |
<math>\Eta(Y|X)=0</math> if and only if the value of <math>Y</math> is completely determined by the value of <math>X</math>. | <math>\Eta(Y|X)=0</math> if and only if the value of <math>Y</math> is completely determined by the value of <math>X</math>. | ||
| − | + | \Eta(X,Y) &= \Eta(X) + \Eta(Y) - \operatorname{I}(X;Y),\, \\ | |
| − | + | Eta (x,y) & = Eta (x) + Eta (y)-操作员名称{ i }(x; y) ,, | |
| + | \operatorname{I}(X;Y) &\le \Eta(X),\, | ||
| + | 操作者名{ i }(x; y) & le Eta (x) ,, | ||
===Conditional entropy of independent random variables=== | ===Conditional entropy of independent random variables=== | ||
| − | + | \end{align}</math> | |
| − | + | 结束{ align } </math > | |
Conversely, <math>\Eta(Y|X) = \Eta(Y)</math> if and only if <math>Y</math> and <math>X</math> are [[independent random variables]]. | Conversely, <math>\Eta(Y|X) = \Eta(Y)</math> if and only if <math>Y</math> and <math>X</math> are [[independent random variables]]. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | where <math>\operatorname{I}(X;Y)</math> is the mutual information between <math>X</math> and <math>Y</math>. | ||
| + | 其中,“数学”和“数学”之间的相互信息。 | ||
===Chain rule=== | ===Chain rule=== | ||
| − | |||
| − | |||
| − | |||
| − | |||
Assume that the combined system determined by two random variables <math>X</math> and <math>Y</math> has [[joint entropy]] <math>\Eta(X,Y)</math>, that is, we need <math>\Eta(X,Y)</math> bits of information on average to describe its exact state. Now if we first learn the value of <math>X</math>, we have gained <math>\Eta(X)</math> bits of information. Once <math>X</math> is known, we only need <math>\Eta(X,Y)-\Eta(X)</math> bits to describe the state of the whole system. This quantity is exactly <math>\Eta(Y|X)</math>, which gives the ''chain rule'' of conditional entropy: | Assume that the combined system determined by two random variables <math>X</math> and <math>Y</math> has [[joint entropy]] <math>\Eta(X,Y)</math>, that is, we need <math>\Eta(X,Y)</math> bits of information on average to describe its exact state. Now if we first learn the value of <math>X</math>, we have gained <math>\Eta(X)</math> bits of information. Once <math>X</math> is known, we only need <math>\Eta(X,Y)-\Eta(X)</math> bits to describe the state of the whole system. This quantity is exactly <math>\Eta(Y|X)</math>, which gives the ''chain rule'' of conditional entropy: | ||
| − | + | For independent <math>X</math> and <math>Y</math>: | |
| − | |||
| − | |||
| − | |||
| + | 对于独立的《数学》和《数学》 : | ||
| 第347行: | 第285行: | ||
:<math>\Eta(Y|X)\, = \, \Eta(X,Y)- \Eta(X).</math><ref name=cover1991 />{{rp|17}} | :<math>\Eta(Y|X)\, = \, \Eta(X,Y)- \Eta(X).</math><ref name=cover1991 />{{rp|17}} | ||
| − | <math>\Eta(Y|X) | + | <math>\Eta(Y|X) = \Eta(Y) </math> and <math>\Eta(X|Y) = \Eta(X) \, </math> |
| − | |||
| − | |||
| − | |||
| + | Eta (y | x) = Eta (y) </math > and < math > Eta (x | y) = Eta (x) ,</math > | ||
| 第357行: | 第293行: | ||
The chain rule follows from the above definition of conditional entropy: | The chain rule follows from the above definition of conditional entropy: | ||
| − | + | Although the specific-conditional entropy <math>\Eta(X|Y=y)</math> can be either less or greater than <math>\Eta(X)</math> for a given random variate <math>y</math> of <math>Y</math>, <math>\Eta(X|Y)</math> can never exceed <math>\Eta(X)</math>. | |
| − | |||
| − | |||
| − | |||
| + | 虽然对于给定的随机变量来说,特定条件熵的 Eta (x | y = y) </math > </math > 可能比 </math > Eta (x) </math > </math > ,< math > Eta (x | y) </math > 不能超过 math > Eta (x) </math > 。 | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| − | |||
| − | |||
| − | |||
| − | |||
\Eta(Y|X) &= \sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log \left(\frac{p(x)}{p(x,y)} \right) \\[4pt] | \Eta(Y|X) &= \sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log \left(\frac{p(x)}{p(x,y)} \right) \\[4pt] | ||
| − | + | &= \sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)(\log (p(x))-\log (p(x,y))) \\[4pt] | |
| − | + | The above definition is for discrete random variables. The continuous version of discrete conditional entropy is called conditional differential (or continuous) entropy. Let <math>X</math> and <math>Y</math> be a continuous random variables with a joint probability density function <math>f(x,y)</math>. The differential conditional entropy <math>h(X|Y)</math> is defined as | |
| − | + | 上面的定义适用于离散随机变量。离散条件熵的连续形式称为条件微分(或连续)熵。设 x 是连续随机变量,f (x,y)是连续随机概率密度函数。微分条件熵 < math > h (x | y) </math > 被定义为 | |
&= -\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log (p(x,y)) + \sum_{x\in\mathcal X, y\in\mathcal Y}{p(x,y)\log(p(x))} \\[4pt] | &= -\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log (p(x,y)) + \sum_{x\in\mathcal X, y\in\mathcal Y}{p(x,y)\log(p(x))} \\[4pt] | ||
| − | |||
| − | |||
& = \Eta(X,Y) + \sum_{x \in \mathcal X} p(x)\log (p(x) ) \\[4pt] | & = \Eta(X,Y) + \sum_{x \in \mathcal X} p(x)\log (p(x) ) \\[4pt] | ||
| − | + | {{Equation box 1 | |
| − | + | {方程式方框1 | |
& = \Eta(X,Y) - \Eta(X). | & = \Eta(X,Y) - \Eta(X). | ||
| − | + | |indent = | |
| − | + | 2012年10月22日 | |
\end{align}</math> | \end{align}</math> | ||
| − | + | |title= | |
| − | + | 2012年10月11日 | |
| + | |equation = }} | ||
| + | | equation = } | ||
In general, a chain rule for multiple random variables holds: | In general, a chain rule for multiple random variables holds: | ||
| − | + | |cellpadding= 6 | |
| − | + | 6 | |
| + | |border | ||
| + | 边界 | ||
:<math> \Eta(X_1,X_2,\ldots,X_n) = | :<math> \Eta(X_1,X_2,\ldots,X_n) = | ||
| − | + | |border colour = #0073CF | |
| − | + | 0073CF | |
\sum_{i=1}^n \Eta(X_i | X_1, \ldots, X_{i-1}) </math><ref name=cover1991 />{{rp|22}} | \sum_{i=1}^n \Eta(X_i | X_1, \ldots, X_{i-1}) </math><ref name=cover1991 />{{rp|22}} | ||
| − | + | |background colour=#F5FFFA}} | |
| − | |||
| − | |||
| − | |||
| + | 5/fffa }} | ||
| 第433行: | 第363行: | ||
It has a similar form to [[Chain rule (probability)|chain rule]] in probability theory, except that addition instead of multiplication is used. | It has a similar form to [[Chain rule (probability)|chain rule]] in probability theory, except that addition instead of multiplication is used. | ||
| − | |||
| − | |||
| + | In contrast to the conditional entropy for discrete random variables, the conditional differential entropy may be negative. | ||
| − | + | 与离散随机变量的条件熵相反,条件微分熵可能是负的。 | |
| − | |||
| − | |||
| − | |||
===Bayes' rule=== | ===Bayes' rule=== | ||
| − | |||
| − | |||
[[Bayes' rule]] for conditional entropy states | [[Bayes' rule]] for conditional entropy states | ||
| − | + | As in the discrete case there is a chain rule for differential entropy: | |
| − | + | 在离散情况下,微分熵有一个链式规则: | |
:<math>\Eta(Y|X) \,=\, \Eta(X|Y) - \Eta(X) + \Eta(Y).</math> | :<math>\Eta(Y|X) \,=\, \Eta(X|Y) - \Eta(X) + \Eta(Y).</math> | ||
| − | <math> | + | <math>h(Y|X)\,=\,h(X,Y)-h(X)</math> |
| − | + | H (y | x) ,= ,h (x,y)-h (x) | |
| + | Notice however that this rule may not be true if the involved differential entropies do not exist or are infinite. | ||
| + | 然而,请注意,如果所涉及的微分熵不存在或者是无限的,那么这个规则可能不成立。 | ||
''Proof.'' <math>\Eta(Y|X) = \Eta(X,Y) - \Eta(X)</math> and <math>\Eta(X|Y) = \Eta(Y,X) - \Eta(Y)</math>. Symmetry entails <math>\Eta(X,Y) = \Eta(Y,X)</math>. Subtracting the two equations implies Bayes' rule. | ''Proof.'' <math>\Eta(Y|X) = \Eta(X,Y) - \Eta(X)</math> and <math>\Eta(X|Y) = \Eta(Y,X) - \Eta(Y)</math>. Symmetry entails <math>\Eta(X,Y) = \Eta(Y,X)</math>. Subtracting the two equations implies Bayes' rule. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Joint differential entropy is also used in the definition of the mutual information between continuous random variables: | ||
| + | 联合微分熵也用于连续随机变量之间互信息的定义: | ||
If <math>Y</math> is [[Conditional independence|conditionally independent]] of <math>Z</math> given <math>X</math> we have: | If <math>Y</math> is [[Conditional independence|conditionally independent]] of <math>Z</math> given <math>X</math> we have: | ||
| − | + | <math>\operatorname{I}(X,Y)=h(X)-h(X|Y)=h(Y)-h(Y|X)</math> | |
| − | |||
| − | |||
| − | |||
| + | (x,y) = h (x)-h (x | y) = h (y)-h (y | x) </math > | ||
| 第485行: | 第407行: | ||
:<math>\Eta(Y|X,Z) \,=\, \Eta(Y|X).</math> | :<math>\Eta(Y|X,Z) \,=\, \Eta(Y|X).</math> | ||
| − | <math> | + | <math>h(X|Y) \le h(X)</math> with equality if and only if <math>X</math> and <math>Y</math> are independent. |
| − | + | 当且仅当 < math > x </math > 和 < math > y </math > 是独立的。 | |
| − | |||
| − | |||
| − | |||
| − | |||
===Other properties=== | ===Other properties=== | ||
| − | |||
| − | |||
For any <math>X</math> and <math>Y</math>: | For any <math>X</math> and <math>Y</math>: | ||
| − | For any <math>X</math> and <math> | + | The conditional differential entropy yields a lower bound on the expected squared error of an estimator. For any random variable <math>X</math>, observation <math>Y</math> and estimator <math>\widehat{X}</math> the following holds: |
| − | + | 条件微分熵对估计量的期望平方误差产生一个下限。对于任何一个随机变量,观察值 < math > y </math > 和估计值 < math > widedhat { x } </math > ,下面是: | |
:<math display="block">\begin{align} | :<math display="block">\begin{align} | ||
| − | <math display="block">\ | + | <math display="block">\mathbb{E}\left[\bigl(X - \widehat{X}{(Y)}\bigr)^2\right] |
| − | + | < math display = " block" > mathbb { e } left [ bigl (x-widehat { x }{(y)} bigr) ^ 2 right ] | |
\Eta(Y|X) &\le \Eta(Y) \, \\ | \Eta(Y|X) &\le \Eta(Y) \, \\ | ||
| − | + | \ge \frac{1}{2\pi e}e^{2h(X|Y)}</math> | |
| − | + | 1}{2 pi e } e ^ {2 h (x | y)} </math > | |
\Eta(X,Y) &= \Eta(X|Y) + \Eta(Y|X) + \operatorname{I}(X;Y),\qquad \\ | \Eta(X,Y) &= \Eta(X|Y) + \Eta(Y|X) + \operatorname{I}(X;Y),\qquad \\ | ||
| − | |||
| − | |||
| − | |||
| − | |||
\Eta(X,Y) &= \Eta(X) + \Eta(Y) - \operatorname{I}(X;Y),\, \\ | \Eta(X,Y) &= \Eta(X) + \Eta(Y) - \operatorname{I}(X;Y),\, \\ | ||
| − | + | This is related to the uncertainty principle from quantum mechanics. | |
| − | + | 这与量子力学的不确定性原理有关。 | |
| − | |||
| − | |||
\operatorname{I}(X;Y) &\le \Eta(X),\, | \operatorname{I}(X;Y) &\le \Eta(X),\, | ||
| − | |||
| − | |||
| − | |||
| − | |||
\end{align}</math> | \end{align}</math> | ||
| − | |||
| − | |||
| + | In quantum information theory, the conditional entropy is generalized to the conditional quantum entropy. The latter can take negative values, unlike its classical counterpart. | ||
| + | 在量子信息论中,条件熵被推广为条件量子熵。后者可以采取负值,不像它的古典对应物。 | ||
where <math>\operatorname{I}(X;Y)</math> is the [[mutual information]] between <math>X</math> and <math>Y</math>. | where <math>\operatorname{I}(X;Y)</math> is the [[mutual information]] between <math>X</math> and <math>Y</math>. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
For independent <math>X</math> and <math>Y</math>: | For independent <math>X</math> and <math>Y</math>: | ||
| − | |||
| − | |||
| − | |||
| − | |||
:<math>\Eta(Y|X) = \Eta(Y) </math> and <math>\Eta(X|Y) = \Eta(X) \, </math> | :<math>\Eta(Y|X) = \Eta(Y) </math> and <math>\Eta(X|Y) = \Eta(X) \, </math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| 第577行: | 第465行: | ||
Although the specific-conditional entropy <math>\Eta(X|Y=y)</math> can be either less or greater than <math>\Eta(X)</math> for a given [[random variate]] <math>y</math> of <math>Y</math>, <math>\Eta(X|Y)</math> can never exceed <math>\Eta(X)</math>. | Although the specific-conditional entropy <math>\Eta(X|Y=y)</math> can be either less or greater than <math>\Eta(X)</math> for a given [[random variate]] <math>y</math> of <math>Y</math>, <math>\Eta(X|Y)</math> can never exceed <math>\Eta(X)</math>. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Conditional differential entropy == | == Conditional differential entropy == | ||
| − | |||
| − | |||
=== Definition === | === Definition === | ||
| − | |||
| − | |||
| − | |||
| − | |||
The above definition is for discrete random variables. The continuous version of discrete conditional entropy is called ''conditional differential (or continuous) entropy''. Let <math>X</math> and <math>Y</math> be a continuous random variables with a [[joint probability density function]] <math>f(x,y)</math>. The differential conditional entropy <math>h(X|Y)</math> is defined as<ref name=cover1991 />{{rp|249}} | The above definition is for discrete random variables. The continuous version of discrete conditional entropy is called ''conditional differential (or continuous) entropy''. Let <math>X</math> and <math>Y</math> be a continuous random variables with a [[joint probability density function]] <math>f(x,y)</math>. The differential conditional entropy <math>h(X|Y)</math> is defined as<ref name=cover1991 />{{rp|249}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{Equation box 1 | {{Equation box 1 | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Category:Entropy and information | Category:Entropy and information | ||
| 第831行: | 第481行: | ||
类别: 熵和信息 | 类别: 熵和信息 | ||
| − | + | |indent = | |
Category:Information theory | Category:Information theory | ||
2020年10月25日 (日) 16:07的版本
此词条暂由彩云小译翻译,未经人工整理和审校,带来阅读不便,请见谅。
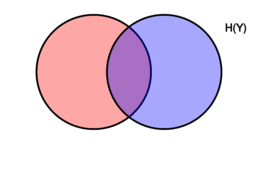
[[Venn diagram showing additive and subtractive relationships various information measures associated with correlated variables [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math]. The area contained by both circles is the joint entropy [math]\displaystyle{ \Eta(X,Y) }[/math]. The circle on the left (red and violet) is the individual entropy [math]\displaystyle{ \Eta(X) }[/math], with the red being the conditional entropy [math]\displaystyle{ \Eta(X|Y) }[/math]. The circle on the right (blue and violet) is [math]\displaystyle{ \Eta(Y) }[/math], with the blue being [math]\displaystyle{ \Eta(Y|X) }[/math]. The violet is the mutual information [math]\displaystyle{ \operatorname{I}(X;Y) }[/math].]]
文恩图显示了相加和相减的关系,各种信息测量与相关变量相关。两个圆圈所包含的区域是联合熵。左边的圆圈(红色和紫色)代表个体熵。左边的圆圈代表个体熵。右边的圆圈代表个体熵。右边的圆圈代表个体熵。右边的圆圈代表个体熵。右边的圆圈代表个体熵。右边的圆圈代表个体熵。右边的圆圈代表个体熵。右边的圆圈代表个体熵。右边的圆圈代表个体熵。右边的圆圈代表个体。右边的圆圈(蓝色和紫色)是 < math > Eta (y) </math > ,蓝色的是 < math > Eta (y | x) </math > 。紫色是共同的信息[ math > 操作者名称{ i }(x; y) </math > ]
In information theory, the conditional entropy quantifies the amount of information needed to describe the outcome of a random variable [math]\displaystyle{ Y }[/math] given that the value of another random variable [math]\displaystyle{ X }[/math] is known. Here, information is measured in shannons, nats, or hartleys. The entropy of [math]\displaystyle{ Y }[/math] conditioned on [math]\displaystyle{ X }[/math] is written as [math]\displaystyle{ \Eta(Y|X) }[/math].
In information theory, the conditional entropy quantifies the amount of information needed to describe the outcome of a random variable [math]\displaystyle{ Y }[/math] given that the value of another random variable [math]\displaystyle{ X }[/math] is known. Here, information is measured in shannons, nats, or hartleys. The entropy of [math]\displaystyle{ Y }[/math] conditioned on [math]\displaystyle{ X }[/math] is written as [math]\displaystyle{ \Eta(Y|X) }[/math].
在信息论中,如果另一个随机变量的值是已知的,那么条件熵就会量化描述一个随机变量的结果所需的信息量。在这里,信息是用夏农、纳特斯或哈特利来衡量的。“数学”的熵取决于“数学” ,“ x”表示“数学” ,“埃塔”表示“数学”。
Definition
The conditional entropy of [math]\displaystyle{ Y }[/math] given [math]\displaystyle{ X }[/math] is defined as
The conditional entropy of [math]\displaystyle{ Y }[/math] given [math]\displaystyle{ X }[/math] is defined as
给定的 x 条件熵被定义为
{{Equation box 1
{{Equation box 1
{方程式方框1
|indent =
|indent =
2012年10月22日
|title=
|title=
2012年10月11日
|equation =
[math]\displaystyle{ \Eta(Y|X)\ = -\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log \frac {p(x,y)} {p(x)} }[/math]
|
|
(Eq.1) |
|equation = }}
| equation = }
|cellpadding= 6
|cellpadding= 6
6
|border
|border
边界
|border colour = #0073CF
|border colour = #0073CF
0073CF
|background colour=#F5FFFA}}
|background colour=#F5FFFA}}
5/fffa }}
where [math]\displaystyle{ \mathcal X }[/math] and [math]\displaystyle{ \mathcal Y }[/math] denote the support sets of [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math].
where [math]\displaystyle{ \mathcal X }[/math] and [math]\displaystyle{ \mathcal Y }[/math] denote the support sets of [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math].
这里 < math > 数学 x </math > 和 < math > > 数学 y </math > 表示 < math > x </math > 和 < math > y </math > 的支持集。
Note: It is conventioned that the expressions [math]\displaystyle{ 0 \log 0 }[/math] and [math]\displaystyle{ 0 \log c/0 }[/math] for fixed [math]\displaystyle{ c \gt 0 }[/math] should be treated as being equal to zero. This is because [math]\displaystyle{ \lim_{\theta\to0^+} \theta\, \log \,c/\theta = 0 }[/math] and [math]\displaystyle{ \lim_{\theta\to0^+} \theta\, \log \theta = 0 }[/math][1]
Note: It is conventioned that the expressions [math]\displaystyle{ 0 \log 0 }[/math] and [math]\displaystyle{ 0 \log c/0 }[/math] for fixed [math]\displaystyle{ c \gt 0 }[/math] should be treated as being equal to zero. This is because [math]\displaystyle{ \lim_{\theta\to0^+} \theta\, \log \,c/\theta = 0 }[/math] and [math]\displaystyle{ \lim_{\theta\to0^+} \theta\, \log \theta = 0 }[/math]
注意: 常规的表达式 < math > 0 log 0 </math > 和 < math > 0 log c/0 </math > 对于 fixed < math > c > 0 </math > 应该被视为等于零。这是因为 < math > lim { theta to0 ^ + } theta,log,c/theta = 0 </math > 和 < math > lim { theta to0 ^ + } theta,log theta = 0 </math >
Intuitive explanation of the definition :
The chain rule follows from the above definition of conditional entropy:
链式规则遵循了上述条件熵的定义:
According to the definition, [math]\displaystyle{ \displaystyle H( Y|X) =\mathbb{E}( \ f( X,Y) \ ) }[/math] where [math]\displaystyle{ \displaystyle f:( x,y) \ \rightarrow -\log( \ p( y|x) \ ) . }[/math] [math]\displaystyle{ \displaystyle f }[/math] associates to [math]\displaystyle{ \displaystyle ( x,y) }[/math] the information content of [math]\displaystyle{ \displaystyle ( Y=y) }[/math] given [math]\displaystyle{ \displaystyle (X=x) }[/math], which is the amount of information needed to describe the event [math]\displaystyle{ \displaystyle (Y=y) }[/math] given [math]\displaystyle{ (X=x) }[/math]. According to the law of large numbers, [math]\displaystyle{ \displaystyle H(Y|X) }[/math] is the arithmetic mean of a large number of independent realizations of [math]\displaystyle{ \displaystyle f(X,Y) }[/math].
[math]\displaystyle{ \begin{align} 1.1.1.2.2.2.2.2.2.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.4.3.3.3.3.3.3.3.3.3.3.3.4.3.3.3.3.3.3.3.3.3 == Motivation == \Eta(Y|X) &= \sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log \left(\frac{p(x)}{p(x,y)} \right) \\[4pt] Eta (y | x) & = sum _ { x in mathcal x,y in mathcal y } p (x,y) log left (frac { p (x)}{ p (x,y)} right)[4 pt ] Let \lt math\gt \Eta(Y|X=x) }[/math] be the entropy of the discrete random variable [math]\displaystyle{ Y }[/math] conditioned on the discrete random variable [math]\displaystyle{ X }[/math] taking a certain value [math]\displaystyle{ x }[/math]. Denote the support sets of [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] by [math]\displaystyle{ \mathcal X }[/math] and [math]\displaystyle{ \mathcal Y }[/math]. Let [math]\displaystyle{ Y }[/math] have probability mass function [math]\displaystyle{ p_Y{(y)} }[/math]. The unconditional entropy of [math]\displaystyle{ Y }[/math] is calculated as [math]\displaystyle{ \Eta(Y) := \mathbb{E}[\operatorname{I}(Y)] }[/math], i.e.
&= \sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)(\log (p(x))-\log (p(x,y))) \\[4pt]
& = sum _ { x in mathcal x,y in mathcal y } p (x,y)(log (p (x))-log (p (x,y)))[4 pt ]
&= -\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log (p(x,y)) + \sum_{x\in\mathcal X, y\in\mathcal Y}{p(x,y)\log(p(x))} \\[4pt]
& =-sum _ { x in mathcal x,y in mathcal y } p (x,y) log (p (x,y)) + sum _ { x in mathcal x,y in mathcal y }{ p (x,y) log (p (x))}[4 pt ]
- [math]\displaystyle{ \Eta(Y) = \sum_{y\in\mathcal Y} {\mathrm{Pr}(Y=y)\,\mathrm{I}(y)} & = \Eta(X,Y) + \sum_{x \in \mathcal X} p(x)\log (p(x) ) \\[4pt] & = Eta (x,y) + sum _ { x in mathcal x } p (x) log (p (x))[4 pt ] = -\sum_{y\in\mathcal Y} {p_Y(y) \log_2{p_Y(y)}}, }[/math]
& = \Eta(X,Y) - \Eta(X).
& = Eta (x,y)-Eta (x).
\end{align}</math>
结束{ align } </math >
where [math]\displaystyle{ \operatorname{I}(y_i) }[/math] is the information content of the outcome of [math]\displaystyle{ Y }[/math] taking the value [math]\displaystyle{ y_i }[/math]. The entropy of [math]\displaystyle{ Y }[/math] conditioned on [math]\displaystyle{ X }[/math] taking the value [math]\displaystyle{ x }[/math] is defined analogously by conditional expectation:
In general, a chain rule for multiple random variables holds:
一般来说,多个随机变量的链式规则适用于:
- [math]\displaystyle{ \Eta(Y|X=x) = -\sum_{y\in\mathcal Y} {\Pr(Y = y|X=x) \log_2{\Pr(Y = y|X=x)}}. }[/math]
[math]\displaystyle{ \Eta(X_1,X_2,\ldots,X_n) = \lt math \gt Eta (x1,x2,ldots,xn) = Note that \lt math\gt \Eta(Y|X) }[/math] is the result of averaging [math]\displaystyle{ \Eta(Y|X=x) }[/math] over all possible values [math]\displaystyle{ x }[/math] that [math]\displaystyle{ X }[/math] may take. Also, if the above sum is taken over a sample [math]\displaystyle{ y_1, \dots, y_n }[/math], the expected value [math]\displaystyle{ E_X[ \Eta(y_1, \dots, y_n \mid X = x)] }[/math] is known in some domains as equivocation.[2]
\sum_{i=1}^n \Eta(X_i | X_1, \ldots, X_{i-1}) </math>
Sum { i = 1} ^ n Eta (x _ i | x _ 1,ldots,x _ { i-1}) </math >
Given discrete random variables [math]\displaystyle{ X }[/math] with image [math]\displaystyle{ \mathcal X }[/math] and [math]\displaystyle{ Y }[/math] with image [math]\displaystyle{ \mathcal Y }[/math], the conditional entropy of [math]\displaystyle{ Y }[/math] given [math]\displaystyle{ X }[/math] is defined as the weighted sum of [math]\displaystyle{ \Eta(Y|X=x) }[/math] for each possible value of [math]\displaystyle{ x }[/math], using [math]\displaystyle{ p(x) }[/math] as the weights:[3]:15
It has a similar form to chain rule in probability theory, except that addition instead of multiplication is used.
除了用加法代替乘法之外,它的形式与概率论的链式法则相似。
- [math]\displaystyle{ \begin{align} Bayes' rule for conditional entropy states 条件熵的贝叶斯规则 \Eta(Y|X)\ &\equiv \sum_{x\in\mathcal X}\,p(x)\,\Eta(Y|X=x)\\ \lt math\gt \Eta(Y|X) \,=\, \Eta(X|Y) - \Eta(X) + \Eta(Y). }[/math]
[数学] Eta (y | x) ,= ,Eta (x | y)-Eta (x) + Eta (y)
& =-\sum_{x\in\mathcal X} p(x)\sum_{y\in\mathcal Y}\,p(y|x)\,\log\, p(y|x)\\
& =-\sum_{x\in\mathcal X}\sum_{y\in\mathcal Y}\,p(x,y)\,\log\,p(y|x)\\
Proof. [math]\displaystyle{ \Eta(Y|X) = \Eta(X,Y) - \Eta(X) }[/math] and [math]\displaystyle{ \Eta(X|Y) = \Eta(Y,X) - \Eta(Y) }[/math]. Symmetry entails [math]\displaystyle{ \Eta(X,Y) = \Eta(Y,X) }[/math]. Subtracting the two equations implies Bayes' rule.
证据。Eta (y | x) = Eta (x,y)-Eta (x) | math > Eta (x | y) = Eta (y,x)-Eta (y).对称意味着 Eta (x,y) = Eta (y,x)。减去这两个方程就得到了贝叶斯定律。
& =-\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log\,p(y|x)\\
& =-\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log \frac {p(x,y)} {p(x)}. \\
If [math]\displaystyle{ Y }[/math] is conditionally independent of [math]\displaystyle{ Z }[/math] given [math]\displaystyle{ X }[/math] we have:
如果[数学] y </math > 是条件独立于[数学] z </math > 给定 < 数学 > x </math > 我们有:
& = \sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log \frac {p(x)} {p(x,y)}. \\
\end{align}
[math]\displaystyle{ \Eta(Y|X,Z) \,=\, \Eta(Y|X). }[/math]
[ math ] Eta (y | x,z) ,= ,Eta (y | x)
</math>
For any [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math]:
对于任意的 < math > x </math > 和 < math > > y </math > :
[math]\displaystyle{ \begin{align} (数学显示 = “ block” \gt begin { align }) ==Properties== \Eta(Y|X) &\le \Eta(Y) \, \\ 埃塔(y | x)及埃塔(y) , ===Conditional entropy equals zero=== \Eta(X,Y) &= \Eta(X|Y) + \Eta(Y|X) + \operatorname{I}(X;Y),\qquad \\ eta (x,y) & = Eta (x | y) + Eta (y | x) + 操作数名{ i }(x; y) ,qquad \lt math\gt \Eta(Y|X)=0 }[/math] if and only if the value of [math]\displaystyle{ Y }[/math] is completely determined by the value of [math]\displaystyle{ X }[/math].
\Eta(X,Y) &= \Eta(X) + \Eta(Y) - \operatorname{I}(X;Y),\, \\
Eta (x,y) & = Eta (x) + Eta (y)-操作员名称{ i }(x; y) ,,
\operatorname{I}(X;Y) &\le \Eta(X),\,
操作者名{ i }(x; y) & le Eta (x) ,,
Conditional entropy of independent random variables
\end{align}</math>
结束{ align } </math >
Conversely, [math]\displaystyle{ \Eta(Y|X) = \Eta(Y) }[/math] if and only if [math]\displaystyle{ Y }[/math] and [math]\displaystyle{ X }[/math] are independent random variables.
where [math]\displaystyle{ \operatorname{I}(X;Y) }[/math] is the mutual information between [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math].
其中,“数学”和“数学”之间的相互信息。
Chain rule
Assume that the combined system determined by two random variables [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] has joint entropy [math]\displaystyle{ \Eta(X,Y) }[/math], that is, we need [math]\displaystyle{ \Eta(X,Y) }[/math] bits of information on average to describe its exact state. Now if we first learn the value of [math]\displaystyle{ X }[/math], we have gained [math]\displaystyle{ \Eta(X) }[/math] bits of information. Once [math]\displaystyle{ X }[/math] is known, we only need [math]\displaystyle{ \Eta(X,Y)-\Eta(X) }[/math] bits to describe the state of the whole system. This quantity is exactly [math]\displaystyle{ \Eta(Y|X) }[/math], which gives the chain rule of conditional entropy:
For independent [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math]:
对于独立的《数学》和《数学》 :
- [math]\displaystyle{ \Eta(Y|X)\, = \, \Eta(X,Y)- \Eta(X). }[/math][3]:17
[math]\displaystyle{ \Eta(Y|X) = \Eta(Y) }[/math] and [math]\displaystyle{ \Eta(X|Y) = \Eta(X) \, }[/math]
Eta (y | x) = Eta (y) </math > and < math > Eta (x | y) = Eta (x) ,</math >
The chain rule follows from the above definition of conditional entropy:
Although the specific-conditional entropy [math]\displaystyle{ \Eta(X|Y=y) }[/math] can be either less or greater than [math]\displaystyle{ \Eta(X) }[/math] for a given random variate [math]\displaystyle{ y }[/math] of [math]\displaystyle{ Y }[/math], [math]\displaystyle{ \Eta(X|Y) }[/math] can never exceed [math]\displaystyle{ \Eta(X) }[/math].
虽然对于给定的随机变量来说,特定条件熵的 Eta (x | y = y) </math > </math > 可能比 </math > Eta (x) </math > </math > ,< math > Eta (x | y) </math > 不能超过 math > Eta (x) </math > 。
- [math]\displaystyle{ \begin{align} \Eta(Y|X) &= \sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log \left(\frac{p(x)}{p(x,y)} \right) \\[4pt] &= \sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)(\log (p(x))-\log (p(x,y))) \\[4pt] The above definition is for discrete random variables. The continuous version of discrete conditional entropy is called conditional differential (or continuous) entropy. Let \lt math\gt X }[/math] and [math]\displaystyle{ Y }[/math] be a continuous random variables with a joint probability density function [math]\displaystyle{ f(x,y) }[/math]. The differential conditional entropy [math]\displaystyle{ h(X|Y) }[/math] is defined as
上面的定义适用于离散随机变量。离散条件熵的连续形式称为条件微分(或连续)熵。设 x 是连续随机变量,f (x,y)是连续随机概率密度函数。微分条件熵 < math > h (x | y) </math > 被定义为
&= -\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log (p(x,y)) + \sum_{x\in\mathcal X, y\in\mathcal Y}{p(x,y)\log(p(x))} \\[4pt]
& = \Eta(X,Y) + \sum_{x \in \mathcal X} p(x)\log (p(x) ) \\[4pt]
{{Equation box 1
{方程式方框1
& = \Eta(X,Y) - \Eta(X).
|indent =
2012年10月22日
\end{align}</math>
|title=
2012年10月11日
|equation = }}
| equation = }
In general, a chain rule for multiple random variables holds:
|cellpadding= 6
6
|border
边界
- [math]\displaystyle{ \Eta(X_1,X_2,\ldots,X_n) = |border colour = #0073CF 0073CF \sum_{i=1}^n \Eta(X_i | X_1, \ldots, X_{i-1}) }[/math][3]:22
|background colour=#F5FFFA}}
5/fffa }}
It has a similar form to chain rule in probability theory, except that addition instead of multiplication is used.
In contrast to the conditional entropy for discrete random variables, the conditional differential entropy may be negative.
与离散随机变量的条件熵相反,条件微分熵可能是负的。
Bayes' rule
Bayes' rule for conditional entropy states
As in the discrete case there is a chain rule for differential entropy:
在离散情况下,微分熵有一个链式规则:
- [math]\displaystyle{ \Eta(Y|X) \,=\, \Eta(X|Y) - \Eta(X) + \Eta(Y). }[/math]
[math]\displaystyle{ h(Y|X)\,=\,h(X,Y)-h(X) }[/math]
H (y | x) ,= ,h (x,y)-h (x)
Notice however that this rule may not be true if the involved differential entropies do not exist or are infinite.
然而,请注意,如果所涉及的微分熵不存在或者是无限的,那么这个规则可能不成立。
Proof. [math]\displaystyle{ \Eta(Y|X) = \Eta(X,Y) - \Eta(X) }[/math] and [math]\displaystyle{ \Eta(X|Y) = \Eta(Y,X) - \Eta(Y) }[/math]. Symmetry entails [math]\displaystyle{ \Eta(X,Y) = \Eta(Y,X) }[/math]. Subtracting the two equations implies Bayes' rule.
Joint differential entropy is also used in the definition of the mutual information between continuous random variables:
联合微分熵也用于连续随机变量之间互信息的定义:
If [math]\displaystyle{ Y }[/math] is conditionally independent of [math]\displaystyle{ Z }[/math] given [math]\displaystyle{ X }[/math] we have:
[math]\displaystyle{ \operatorname{I}(X,Y)=h(X)-h(X|Y)=h(Y)-h(Y|X) }[/math]
(x,y) = h (x)-h (x | y) = h (y)-h (y | x) </math >
- [math]\displaystyle{ \Eta(Y|X,Z) \,=\, \Eta(Y|X). }[/math]
[math]\displaystyle{ h(X|Y) \le h(X) }[/math] with equality if and only if [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] are independent.
当且仅当 < math > x </math > 和 < math > y </math > 是独立的。
Other properties
For any [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math]:
The conditional differential entropy yields a lower bound on the expected squared error of an estimator. For any random variable [math]\displaystyle{ X }[/math], observation [math]\displaystyle{ Y }[/math] and estimator [math]\displaystyle{ \widehat{X} }[/math] the following holds:
条件微分熵对估计量的期望平方误差产生一个下限。对于任何一个随机变量,观察值 < math > y </math > 和估计值 < math > widedhat { x } </math > ,下面是:
- [math]\displaystyle{ \begin{align} \lt math display="block"\gt \mathbb{E}\left[\bigl(X - \widehat{X}{(Y)}\bigr)^2\right] \lt math display = " block" \gt mathbb { e } left [ bigl (x-widehat { x }{(y)} bigr) ^ 2 right ] \Eta(Y|X) &\le \Eta(Y) \, \\ \ge \frac{1}{2\pi e}e^{2h(X|Y)} }[/math]
1}{2 pi e } e ^ {2 h (x | y)} </math >
\Eta(X,Y) &= \Eta(X|Y) + \Eta(Y|X) + \operatorname{I}(X;Y),\qquad \\
\Eta(X,Y) &= \Eta(X) + \Eta(Y) - \operatorname{I}(X;Y),\, \\
This is related to the uncertainty principle from quantum mechanics.
这与量子力学的不确定性原理有关。
\operatorname{I}(X;Y) &\le \Eta(X),\,
\end{align}</math>
In quantum information theory, the conditional entropy is generalized to the conditional quantum entropy. The latter can take negative values, unlike its classical counterpart.
在量子信息论中,条件熵被推广为条件量子熵。后者可以采取负值,不像它的古典对应物。
where [math]\displaystyle{ \operatorname{I}(X;Y) }[/math] is the mutual information between [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math].
For independent [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math]:
- [math]\displaystyle{ \Eta(Y|X) = \Eta(Y) }[/math] and [math]\displaystyle{ \Eta(X|Y) = \Eta(X) \, }[/math]
Although the specific-conditional entropy [math]\displaystyle{ \Eta(X|Y=y) }[/math] can be either less or greater than [math]\displaystyle{ \Eta(X) }[/math] for a given random variate [math]\displaystyle{ y }[/math] of [math]\displaystyle{ Y }[/math], [math]\displaystyle{ \Eta(X|Y) }[/math] can never exceed [math]\displaystyle{ \Eta(X) }[/math].
Conditional differential entropy
Definition
The above definition is for discrete random variables. The continuous version of discrete conditional entropy is called conditional differential (or continuous) entropy. Let [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] be a continuous random variables with a joint probability density function [math]\displaystyle{ f(x,y) }[/math]. The differential conditional entropy [math]\displaystyle{ h(X|Y) }[/math] is defined as[3]:249
{{Equation box 1
Category:Entropy and information
类别: 熵和信息
|indent =
Category:Information theory
范畴: 信息论
This page was moved from wikipedia:en:Conditional entropy. Its edit history can be viewed at 条件熵/edithistory
- ↑ "David MacKay: Information Theory, Pattern Recognition and Neural Networks: The Book". www.inference.org.uk. Retrieved 2019-10-25.
- ↑ Hellman, M.; Raviv, J. (1970). "Probability of error, equivocation, and the Chernoff bound". IEEE Transactions on Information Theory. 16 (4): 368–372.
- ↑ 3.0 3.1 3.2 3.3 T. Cover; J. Thomas (1991). Elements of Information Theory. ISBN 0-471-06259-6. https://archive.org/details/elementsofinform0000cove.