“斑图”的版本间的差异

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
跳到导航 跳到搜索
（Moved page from wikipedia:en:Pattern formation (history)）
 
小 （Moved page from wikipedia:en:Pattern formation (history)）
第1行： 第1行：
−
此词条暂由彩云小译翻译，未经人工整理和审校，带来阅读不便，请见谅。{{Short description|Study of how patterns form by self-organization in nature}}
+
此词条暂由彩云小译翻译，翻译字数共484，未经人工整理和审校，带来阅读不便，请见谅。
−
 
 
  
 +
{{Short description|Study of how patterns form by self-organization in nature}}
  
 
{{Complex systems}}
 
{{Complex systems}}
−
 
−
 
  
 
[[File:Self-organizing-Mechanism-for-Development-of-Space-filling-Neuronal-Dendrites-pcbi.0030212.sv003.ogv|thumb|Pattern formation in a [[computational model]] of [[dendrite]] growth.]]
 
[[File:Self-organizing-Mechanism-for-Development-of-Space-filling-Neuronal-Dendrites-pcbi.0030212.sv003.ogv|thumb|Pattern formation in a [[computational model]] of [[dendrite]] growth.]]
第18行： 第16行：
  
 
模式形成的科学研究的是可见的、(统计学上)有序的自我组织和自然界中相似模式背后的共同原理。
 
模式形成的科学研究的是可见的、(统计学上)有序的自我组织和自然界中相似模式背后的共同原理。
−
 
−
 
  
  
第27行： 第23行：
 
In developmental biology, pattern formation refers to the generation of complex organizations of cell fates in space and time. Pattern formation is controlled by genes. The role of genes in pattern formation is an aspect of morphogenesis, the creation of diverse anatomies from similar genes, now being explored in the science of evolutionary developmental biology or evo-devo. The mechanisms involved are well seen in the anterior-posterior patterning of embryos from the model organism Drosophila melanogaster (a fruit fly), one of the first organisms to have its morphogenesis studied and in the eyespots of butterflies, whose development is a variant of the standard (fruit fly) mechanism.
 
In developmental biology, pattern formation refers to the generation of complex organizations of cell fates in space and time. Pattern formation is controlled by genes. The role of genes in pattern formation is an aspect of morphogenesis, the creation of diverse anatomies from similar genes, now being explored in the science of evolutionary developmental biology or evo-devo. The mechanisms involved are well seen in the anterior-posterior patterning of embryos from the model organism Drosophila melanogaster (a fruit fly), one of the first organisms to have its morphogenesis studied and in the eyespots of butterflies, whose development is a variant of the standard (fruit fly) mechanism.
  
−
在发育生物学，模式形成指的是细胞在空间和时间中命运的复杂组织的产生。模式的形成是由基因控制的。基因在模式形成中的作用是形态发生的一个方面，即从相似的基因中创造不同的解剖结构，目前正在演化发育生物学或演化发育生物学中探索。其中涉及的机制可以从模式生物黑腹果蝇(一种果蝇)的胚胎前后图案和蝴蝶的眼点中清楚地看到，后者的发育是标准(果蝇)机制的变体。
+
在发育生物学，模式形成指的是细胞在空间和时间中命运的复杂组织的产生。模式的形成是由基因控制的。基因在模式形成中的作用是形态发生的一个方面，即从相似的基因中创造出不同的解剖结构，目前正在演化发育生物学科学或演化发育生物学中探索。模式生物黑腹果蝇(一种果蝇)的胚胎的前后部图案和蝴蝶的眼点都清楚地表明了其中的机制，前者是最早研究其形态发生的生物之一，后者的发育是标准(果蝇)机制的变体。
−
 
 
−
 
 
  
  
  
 
==Examples==
 
==Examples==
−
 
−
==Examples==
 
−
 
−
例子
 
  
 
{{further|Patterns in nature}}
 
{{further|Patterns in nature}}
−
 
−
 
  
 
Examples of pattern formation can be found in biology, chemistry, physics, and mathematics,<ref>Ball, 2009.</ref> and can readily be simulated with computer graphics, as described in turn below.
 
Examples of pattern formation can be found in biology, chemistry, physics, and mathematics,<ref>Ball, 2009.</ref> and can readily be simulated with computer graphics, as described in turn below.
  
−
Examples of pattern formation can be found in biology, chemistry, physics, and mathematics, and can readily be simulated with computer graphics, as described in turn below.
+
Examples of pattern formation can be found in biology, chemistry, physics, and mathematics, In contrast, fir waves occur in forests on mountain slopes after wind disturbance, during regeneration. When trees fall, the trees that they had sheltered become exposed and are in turn more likely to be damaged, so gaps tend to expand downwind. Meanwhile, on the windward side, young trees grow, protected by the wind shadow of the remaining tall trees. In flat terrains additional pattern morphologies appear besides stripes - hexagonal gap patterns and hexagonal spot patterns. Pattern formation in this case is driven by positive feedback loops between local vegetation growth and water transport towards the growth location. The emergence of pattern formation can be studied by mathematical modeling and simulation of the underlying reaction-diffusion system.
  
−
模式形成的例子可以在生物、化学、物理和数学中找到，并且可以很容易地用计算机图形学模拟，下面依次描述。
+
在生物学、化学、物理学和数学中都可以找到模式形成的例子。相反，在风扰动之后，在更新期间，冷杉波发生在山坡上的森林中。当树木倒下的时候，它们曾经庇护过的树木变得暴露，反过来更有可能受到损害，所以缝隙往往在下风处扩大。与此同时，在迎风面，年轻的树木生长，受到剩余高大树木的风影的保护。在平面地形中，除了条纹、六角形缝隙图案和六角形斑点图案外，还出现了其他图案形态。在这种情况下，格局的形成是由当地植被生长和水向生长地点输送之间的正反馈循环驱动的。模式形成的出现可以用潜在的反应扩散系统的数学建模与模拟来研究。
  
  
−
 
−
 
−
 
−
===Biology===
 
  
 
===Biology===
 
===Biology===
−
 
−
生物学
 
  
 
{{further|Evolutionary developmental biology|Morphogenetic field}}
 
{{further|Evolutionary developmental biology|Morphogenetic field}}
−
 
−
 
−
 
−
 
  
  
  
 
Biological patterns such as [[animal markings]], the segmentation of animals, and [[phyllotaxis]] are formed in different ways.<ref>Ball, 2009. ''Shapes'', pp. 231–252.</ref>
 
Biological patterns such as [[animal markings]], the segmentation of animals, and [[phyllotaxis]] are formed in different ways.<ref>Ball, 2009. ''Shapes'', pp. 231–252.</ref>
−
 
−
Biological patterns such as animal markings, the segmentation of animals, and phyllotaxis are formed in different ways.
 
−
 
−
动物标记、动物分节、叶序等生物学模式以不同的方式形成。
 
−
 
−
 
  
  
  
 
In [[developmental biology]], pattern formation describes the mechanism by which initially equivalent cells in a developing tissue in an [[embryo]] assume complex forms and functions.<ref>Ball, 2009. Shapes, pp. 261–290.</ref> [[Embryogenesis]], such as [[Drosophila embryogenesis|of the fruit fly ''Drosophila'']], involves coordinated [[cell fate determination|control of cell fates]].<ref name=Lai>{{cite journal |author=Eric C. Lai |title=Notch signaling: control of cell communication and cell fate |doi=10.1242/dev.01074 |pmid=14973298 |volume=131 |issue=5 |date=March 2004 |pages=965–73 |journal=Development|doi-access=free }}</ref><ref name=Tyler>{{cite journal |title=Cellular pattern formation during retinal regeneration: A role for homotypic control of cell fate acquisition |authors=Melinda J. Tyler, David A. Cameron|journal=Vision Research |volume=47 |issue=4 |pages=501–511 |year=2007 |doi=10.1016/j.visres.2006.08.025 |pmid=17034830}}</ref><ref name=Meinhard>{{cite web|title=Biological pattern formation: How cell[s] talk with each other to achieve reproducible pattern formation |author=Hans Meinhard |agency= Max-Planck-Institut für Entwicklungsbiologie, Tübingen, Germany |url=http://www1.biologie.uni-hamburg.de/b-online/e28_1/pattern.htm |date=2001-10-26 }}</ref> Pattern formation is genetically controlled, and often involves each cell in a field sensing and responding to its position along a [[morphogen]] gradient, followed by short distance cell-to-cell communication through [[cell signaling]] pathways to refine the initial pattern. In this context, a field of cells is the group of cells whose fates are affected by responding to the same set positional information cues. This conceptual model was first described as the [[French flag model]] in the 1960s.<ref>{{cite journal |doi=10.1016/S0022-5193(69)80016-0 |author=Wolpert L |title=Positional information and the spatial pattern of cellular differentiation |journal=J. Theor. Biol. |volume=25 |issue=1 |pages=1–47 |date=October 1969 |pmid=4390734 }}</ref><ref>{{cite book |author=Wolpert, Lewis |title=Principles of development |publisher=Oxford University Press |location=Oxford [Oxfordshire] |year=2007 |isbn=978-0-19-927536-6 |edition=3rd |display-authors=etal}}</ref> More generally, the morphology of organisms is patterned by the mechanisms of [[evolutionary developmental biology]], such as [[heterochrony|changing the timing]] and positioning of specific developmental events in the embryo.<ref>{{cite journal |last1=Hall |first1=B. K. |title=Evo-Devo: evolutionary developmental mechanisms |journal=International Journal of Developmental Biology |date=2003 |volume=47 |issue=7–8 |pages=491–495 |pmid=14756324}}</ref>
 
In [[developmental biology]], pattern formation describes the mechanism by which initially equivalent cells in a developing tissue in an [[embryo]] assume complex forms and functions.<ref>Ball, 2009. Shapes, pp. 261–290.</ref> [[Embryogenesis]], such as [[Drosophila embryogenesis|of the fruit fly ''Drosophila'']], involves coordinated [[cell fate determination|control of cell fates]].<ref name=Lai>{{cite journal |author=Eric C. Lai |title=Notch signaling: control of cell communication and cell fate |doi=10.1242/dev.01074 |pmid=14973298 |volume=131 |issue=5 |date=March 2004 |pages=965–73 |journal=Development|doi-access=free }}</ref><ref name=Tyler>{{cite journal |title=Cellular pattern formation during retinal regeneration: A role for homotypic control of cell fate acquisition |authors=Melinda J. Tyler, David A. Cameron|journal=Vision Research |volume=47 |issue=4 |pages=501–511 |year=2007 |doi=10.1016/j.visres.2006.08.025 |pmid=17034830}}</ref><ref name=Meinhard>{{cite web|title=Biological pattern formation: How cell[s] talk with each other to achieve reproducible pattern formation |author=Hans Meinhard |agency= Max-Planck-Institut für Entwicklungsbiologie, Tübingen, Germany |url=http://www1.biologie.uni-hamburg.de/b-online/e28_1/pattern.htm |date=2001-10-26 }}</ref> Pattern formation is genetically controlled, and often involves each cell in a field sensing and responding to its position along a [[morphogen]] gradient, followed by short distance cell-to-cell communication through [[cell signaling]] pathways to refine the initial pattern. In this context, a field of cells is the group of cells whose fates are affected by responding to the same set positional information cues. This conceptual model was first described as the [[French flag model]] in the 1960s.<ref>{{cite journal |doi=10.1016/S0022-5193(69)80016-0 |author=Wolpert L |title=Positional information and the spatial pattern of cellular differentiation |journal=J. Theor. Biol. |volume=25 |issue=1 |pages=1–47 |date=October 1969 |pmid=4390734 }}</ref><ref>{{cite book |author=Wolpert, Lewis |title=Principles of development |publisher=Oxford University Press |location=Oxford [Oxfordshire] |year=2007 |isbn=978-0-19-927536-6 |edition=3rd |display-authors=etal}}</ref> More generally, the morphology of organisms is patterned by the mechanisms of [[evolutionary developmental biology]], such as [[heterochrony|changing the timing]] and positioning of specific developmental events in the embryo.<ref>{{cite journal |last1=Hall |first1=B. K. |title=Evo-Devo: evolutionary developmental mechanisms |journal=International Journal of Developmental Biology |date=2003 |volume=47 |issue=7–8 |pages=491–495 |pmid=14756324}}</ref>
−
 
−
In developmental biology, pattern formation describes the mechanism by which initially equivalent cells in a developing tissue in an embryo assume complex forms and functions. Embryogenesis, such as of the fruit fly Drosophila, involves coordinated control of cell fates. Pattern formation is genetically controlled, and often involves each cell in a field sensing and responding to its position along a morphogen gradient, followed by short distance cell-to-cell communication through cell signaling pathways to refine the initial pattern. In this context, a field of cells is the group of cells whose fates are affected by responding to the same set positional information cues. This conceptual model was first described as the French flag model in the 1960s. More generally, the morphology of organisms is patterned by the mechanisms of evolutionary developmental biology, such as changing the timing and positioning of specific developmental events in the embryo.
 
−
 
−
在《发育生物学，模式形成描述了胚胎中发育中的组织中最初的等效细胞呈现出复杂形态和功能的机制。胚胎发生，例如果蝇的胚胎发生，涉及到细胞命运的协调控制。模式的形成是遗传控制的，通常涉及每个细胞在一个场感应和响应其位置沿形态梯度，然后通过细胞信号通路进行短距离的细胞间通信，以精炼最初的模式。在这种情况下，一个细胞领域是一组细胞，它们的命运受到相同位置信息线索的响应影响。这种概念模型在20世纪60年代首次被描述为法国国旗模型。更一般地说，生物体的形态是由演化发育生物学的机制构成的，例如改变胚胎中特定发育事件的时间和位置。
 
  
  
  
 +
In the 1980s Lugiato and Lefever developed a model of light propagation in an optical cavity that results in pattern formation by the exploitation of nonlinear effects.
  
 +
在20世纪80年代，Lugiato 和 Lefever 发展了一个光在光学腔中传播的模型，这个模型通过利用非线性效应来形成图案。
  
 
Possible mechanisms of pattern formation in biological systems include the classical [[reaction–diffusion]] model proposed by [[Alan Turing]]<ref>S. Kondo, T. Miura, "Reaction-Diffusion Model as a Framework for Understanding Biological Pattern Formation", Science 24 Sep 2010: Vol. 329, Issue 5999, pp. 1616-1620 DOI: 10.1126/science.1179047</ref> and the more recently found [[elastic instability]] mechanism which is thought to be responsible for the fold patterns on the [[cerebral cortex]] of higher animals, among other things.<ref name="Mercker">{{cite journal |last1=Mercker |first1=M |last2=Brinkmann |first2=F |last3=Marciniak-Czochra |first3=A |last4=Richter |first4=T |title=Beyond Turing: mechanochemical pattern formation in biological tissues. |journal=Biology Direct |date=4 May 2016 |volume=11 |pages=22 |doi=10.1186/s13062-016-0124-7 |pmid=27145826|pmc=4857296 }}</ref><ref>Tallinen et al. Nature Physics 12, 588–593 (2016) doi:10.1038/nphys3632</ref>
 
Possible mechanisms of pattern formation in biological systems include the classical [[reaction–diffusion]] model proposed by [[Alan Turing]]<ref>S. Kondo, T. Miura, "Reaction-Diffusion Model as a Framework for Understanding Biological Pattern Formation", Science 24 Sep 2010: Vol. 329, Issue 5999, pp. 1616-1620 DOI: 10.1126/science.1179047</ref> and the more recently found [[elastic instability]] mechanism which is thought to be responsible for the fold patterns on the [[cerebral cortex]] of higher animals, among other things.<ref name="Mercker">{{cite journal |last1=Mercker |first1=M |last2=Brinkmann |first2=F |last3=Marciniak-Czochra |first3=A |last4=Richter |first4=T |title=Beyond Turing: mechanochemical pattern formation in biological tissues. |journal=Biology Direct |date=4 May 2016 |volume=11 |pages=22 |doi=10.1186/s13062-016-0124-7 |pmid=27145826|pmc=4857296 }}</ref><ref>Tallinen et al. Nature Physics 12, 588–593 (2016) doi:10.1038/nphys3632</ref>
−
 
−
Possible mechanisms of pattern formation in biological systems include the classical reaction–diffusion model proposed by Alan Turing and the more recently found elastic instability mechanism which is thought to be responsible for the fold patterns on the cerebral cortex of higher animals, among other things.
 
−
 
−
生物系统中模式形成的可能机制包括阿兰 · 图灵提出的经典反应扩散模型和最近发现的弹性不稳定机制，该机制被认为对高等动物大脑皮层的折叠模式负有责任。
 
−
 
  
  
  
 +
Bénard cells, laser, cloud formations in stripes or rolls. Ripples in icicles. Washboard patterns on dirtroads. Dendrites in solidification, liquid crystals. Solitons.
  
−
====Growth of colonies====
+
贝纳德细胞，激光，条纹或滚动的云层。冰柱上的涟漪。十字架上的搓板图案。凝固过程中的树枝晶、液晶。孤子。
  
 
====Growth of colonies====
 
====Growth of colonies====
−
 
−
菌落生长
 
  
 
Bacterial colonies show a [[bacterial patterns|large variety of patterns]] formed during colony growth. The resulting shapes depend on the growth conditions. In particular, stresses (hardness of the culture medium, lack of nutrients, etc.) enhance the complexity of the resulting patterns.<ref>Ball, 2009. ''Branches'', pp. 52–59.</ref> Other organisms such as [[slime mould]]s display remarkable patterns caused by the dynamics of chemical signaling.<ref>Ball, 2009. ''Shapes'', pp. 149–151.</ref>
 
Bacterial colonies show a [[bacterial patterns|large variety of patterns]] formed during colony growth. The resulting shapes depend on the growth conditions. In particular, stresses (hardness of the culture medium, lack of nutrients, etc.) enhance the complexity of the resulting patterns.<ref>Ball, 2009. ''Branches'', pp. 52–59.</ref> Other organisms such as [[slime mould]]s display remarkable patterns caused by the dynamics of chemical signaling.<ref>Ball, 2009. ''Shapes'', pp. 149–151.</ref>
−
 
−
Bacterial colonies show a large variety of patterns formed during colony growth. The resulting shapes depend on the growth conditions. In particular, stresses (hardness of the culture medium, lack of nutrients, etc.) enhance the complexity of the resulting patterns. Other organisms such as slime moulds display remarkable patterns caused by the dynamics of chemical signaling.
 
−
 
−
细菌菌落在菌落生长过程中表现出多种多样的形式。产生的形状取决于生长条件。特别是强调(培养基的硬度，缺乏营养等)增加了产生模式的复杂性。其他有机体，如粘菌显示了显着的模式所造成的动态化学信号。
 
−
 
−
 
  
  
第115行： 第73行：
 
====Vegetation patterns====
 
====Vegetation patterns====
  
−
====Vegetation patterns====
+
Sphere packings and coverings. Mathematics underlies the other pattern formation mechanisms listed.
  
−
植被模式
+
球形填料和覆盖物。数学是其他模式形成机制的基础。
  
 
{{Main|patterned vegetation}}
 
{{Main|patterned vegetation}}
−
 
−
 
  
 
[[File:Tiger Bush Niger Corona 1965-12-31.jpg|thumb|[[Tiger bush]] is a [[patterned vegetation|vegetation pattern]] that forms in arid conditions.]]
 
[[File:Tiger Bush Niger Corona 1965-12-31.jpg|thumb|[[Tiger bush]] is a [[patterned vegetation|vegetation pattern]] that forms in arid conditions.]]
  
−
[[Tiger bush is a vegetation pattern that forms in arid conditions.]]
 
  
−
[虎灌木是在干旱条件下形成的植被模式。]
 
  
 +
[[patterned vegetation|Vegetation patterns]] such as [[tiger bush]]<ref name=TigerBush>{{cite book | title=Banded vegetation patterning in arid and semiarid environments | publisher=Springer-Verlag | author=Tongway, D.J., Valentin, C. & Seghieri, J. | year=2001 | location=New York|isbn=978-1461265597}}</ref> and [[fir wave]]s<ref name=FirWave>{{cite web | url=http://tiee.esa.org/vol/v1/figure_sets/disturb/disturb_back4.html | title=Fir Waves: Regeneration in New England Conifer Forests | publisher=TIEE | date=22 February 2004 | accessdate=26 May 2012 | author=D'Avanzo, C.}}</ref> form for different reasons. Tiger bush consists of stripes of bushes on arid slopes in countries such as [[Niger]] where plant growth is limited by rainfall. Each roughly horizontal stripe of vegetation absorbs rainwater from the bare zone immediately above it.<ref name=TigerBush/> In contrast, fir waves occur in forests on mountain slopes after wind disturbance, during regeneration. When trees fall, the trees that they had sheltered become exposed and are in turn more likely to be damaged, so gaps tend to expand downwind. Meanwhile, on the windward side, young trees grow, protected by the wind shadow of the remaining tall trees.<ref name=FirWave/> In flat terrains additional pattern morphologies appear besides stripes - hexagonal gap patterns and hexagonal spot patterns. Pattern formation in this case is driven by positive feedback loops between local vegetation growth and water transport towards the growth location.<ref>{{cite journal |author=Meron, E |title=Vegetation pattern formation: the mechanisms behind the forms |journal=Physics Today |volume=72 |issue=11 | pages=30–36 |year=2019 |doi=10.1063/PT.3.4340}}</ref><ref>{{cite journal |author=Meron, E |title=From Patterns to Function in Living Systems: Dryland Ecosystems as a Case Study|journal=Annual Review of Condensed Matter Physics  |volume=9 | pages=79–103  |year=2018 |doi=10.1146/annurev-conmatphys-033117-053959}}</ref>
  
  
  
 +
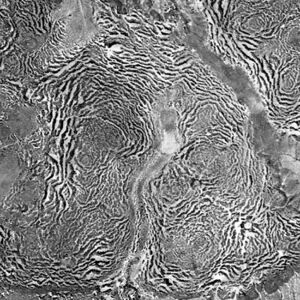
Pattern resembling a [[reaction–diffusion model, produced using sharpen and blur]]
  
−
[[patterned vegetation|Vegetation patterns]] such as [[tiger bush]]<ref name=TigerBush>{{cite book | title=Banded vegetation patterning in arid and semiarid environments | publisher=Springer-Verlag | author=Tongway, D.J., Valentin, C. & Seghieri, J. | year=2001 | location=New York|isbn=978-1461265597}}</ref> and [[fir wave]]s<ref name=FirWave>{{cite web | url=http://tiee.esa.org/vol/v1/figure_sets/disturb/disturb_back4.html | title=Fir Waves: Regeneration in New England Conifer Forests | publisher=TIEE | date=22 February 2004 | accessdate=26 May 2012 | author=D'Avanzo, C.}}</ref> form for different reasons. Tiger bush consists of stripes of bushes on arid slopes in countries such as [[Niger]] where plant growth is limited by rainfall. Each roughly horizontal stripe of vegetation absorbs rainwater from the bare zone immediately above it.<ref name=TigerBush/> In contrast, fir waves occur in forests on mountain slopes after wind disturbance, during regeneration. When trees fall, the trees that they had sheltered become exposed and are in turn more likely to be damaged, so gaps tend to expand downwind. Meanwhile, on the windward side, young trees grow, protected by the wind shadow of the remaining tall trees<ref name=FirWave/>. In flat terrains additional pattern morphologies appear besides stripes - hexagonal gap patterns and hexagonal spot patterns. Pattern formation in this case is driven by positive feedback loops between local vegetation growth and water transport towards the growth location<ref>{{cite journal |author=Meron, E |title=Vegetation pattern formation: the mechanisms behind the forms |journal=Physics Today |volume=72 |issue=11 | pages=30-36 |year=2019 |doi=10.1063/PT.3.4340}}</ref><ref>{{cite journal |author=Meron, E |title=From Patterns to Function in Living Systems: Dryland Ecosystems as a Case Study|journal=Annual Review of Condensed Matter Physics  |volume=9 | pages=79-103  |year=2018 |doi=10.1146/annurev-conmatphys-033117-053959}}</ref>.
+
图案类似于[[反应扩散模型，使用锐化和模糊]]
−
 
 
−
Vegetation patterns such as tiger bush and fir waves form for different reasons. Tiger bush consists of stripes of bushes on arid slopes in countries such as Niger where plant growth is limited by rainfall. Each roughly horizontal stripe of vegetation absorbs rainwater from the bare zone immediately above it..
 
−
 
 
−
植被模式，如虎灌木和冷杉波形成的原因不同。在尼日尔等干旱国家，植物生长受到降雨的限制，虎灌木由干旱斜坡上的带状灌木组成。每一条粗略的水平植被带都可以从其上方的裸露地带吸收雨水。
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
===Chemistry===
 
  
 
===Chemistry===
 
===Chemistry===
−
 
−
化学
 
  
 
{{expand section|date=March 2013}}
 
{{expand section|date=March 2013}}
−
 
−
 
  
 
{{further|reaction–diffusion system|Turing patterns}}Pattern formation has been well studied in chemistry and chemical engineering, including both temperature and concentration patterns.<ref name=":0">{{Cite journal|last=Gupta|first=Ankur|last2=Chakraborty|first2=Saikat|date=January 2009|title=Linear stability analysis of high- and low-dimensional models for describing mixing-limited pattern formation in homogeneous autocatalytic reactors|journal=Chemical Engineering Journal|volume=145|issue=3|pages=399–411|doi=10.1016/j.cej.2008.08.025|issn=1385-8947}}</ref> The [[Brusselator]] model developed by [[Ilya Prigogine]] and collaborators is one such example that exhibits [[Turing instability]].<ref>{{Citation|last=Prigogine|first=I.|title=Self-Organisation in Nonequilibrium Systems: Towards A Dynamics of Complexity|date=1985|work=Bifurcation Analysis: Principles, Applications and Synthesis|pages=3–12|editor-last=Hazewinkel|editor-first=M.|publisher=Springer Netherlands|doi=10.1007/978-94-009-6239-2_1|isbn=9789400962392|last2=Nicolis|first2=G.|editor2-last=Jurkovich|editor2-first=R.|editor3-last=Paelinck|editor3-first=J. H. P.}}</ref> Pattern formation in chemical systems often involve [[Chemical oscillator|oscillatory chemical kinetics]] or [[Autocatalysis|autocatalytic reactions]]<ref name=":1">{{Cite journal|last=Gupta|first=Ankur|last2=Chakraborty|first2=Saikat|date=2008-01-19|title=Dynamic Simulation of Mixing-Limited Pattern Formation in Homogeneous Autocatalytic Reactions|journal=Chemical Product and Process Modeling|volume=3|issue=2|doi=10.2202/1934-2659.1135|issn=1934-2659}}</ref> such as [[Belousov–Zhabotinsky reaction]] or [[Briggs–Rauscher reaction]]. In industrial applications such as chemical reactors, pattern formation can lead to temperature hot spots which can reduce the yield or create hazardous safety problems such as a [[thermal runaway]].<ref>{{Cite journal|last=Marwaha|first=Bharat|last2=Sundarram|first2=Sandhya|last3=Luss|first3=Dan|date=September 2004|title=Dynamics of Transversal Hot Zones in Shallow Packed-Bed Reactors†|journal=The Journal of Physical Chemistry B|volume=108|issue=38|pages=14470–14476|doi=10.1021/jp049803p|issn=1520-6106}}</ref><ref name=":0" /> The emergence of pattern formation can be studied by mathematical modeling and simulation of the underlying [[Reaction–diffusion system|reaction-diffusion system]].<ref name=":0" /><ref name=":1" />
 
{{further|reaction–diffusion system|Turing patterns}}Pattern formation has been well studied in chemistry and chemical engineering, including both temperature and concentration patterns.<ref name=":0">{{Cite journal|last=Gupta|first=Ankur|last2=Chakraborty|first2=Saikat|date=January 2009|title=Linear stability analysis of high- and low-dimensional models for describing mixing-limited pattern formation in homogeneous autocatalytic reactors|journal=Chemical Engineering Journal|volume=145|issue=3|pages=399–411|doi=10.1016/j.cej.2008.08.025|issn=1385-8947}}</ref> The [[Brusselator]] model developed by [[Ilya Prigogine]] and collaborators is one such example that exhibits [[Turing instability]].<ref>{{Citation|last=Prigogine|first=I.|title=Self-Organisation in Nonequilibrium Systems: Towards A Dynamics of Complexity|date=1985|work=Bifurcation Analysis: Principles, Applications and Synthesis|pages=3–12|editor-last=Hazewinkel|editor-first=M.|publisher=Springer Netherlands|doi=10.1007/978-94-009-6239-2_1|isbn=9789400962392|last2=Nicolis|first2=G.|editor2-last=Jurkovich|editor2-first=R.|editor3-last=Paelinck|editor3-first=J. H. P.}}</ref> Pattern formation in chemical systems often involve [[Chemical oscillator|oscillatory chemical kinetics]] or [[Autocatalysis|autocatalytic reactions]]<ref name=":1">{{Cite journal|last=Gupta|first=Ankur|last2=Chakraborty|first2=Saikat|date=2008-01-19|title=Dynamic Simulation of Mixing-Limited Pattern Formation in Homogeneous Autocatalytic Reactions|journal=Chemical Product and Process Modeling|volume=3|issue=2|doi=10.2202/1934-2659.1135|issn=1934-2659}}</ref> such as [[Belousov–Zhabotinsky reaction]] or [[Briggs–Rauscher reaction]]. In industrial applications such as chemical reactors, pattern formation can lead to temperature hot spots which can reduce the yield or create hazardous safety problems such as a [[thermal runaway]].<ref>{{Cite journal|last=Marwaha|first=Bharat|last2=Sundarram|first2=Sandhya|last3=Luss|first3=Dan|date=September 2004|title=Dynamics of Transversal Hot Zones in Shallow Packed-Bed Reactors†|journal=The Journal of Physical Chemistry B|volume=108|issue=38|pages=14470–14476|doi=10.1021/jp049803p|issn=1520-6106}}</ref><ref name=":0" /> The emergence of pattern formation can be studied by mathematical modeling and simulation of the underlying [[Reaction–diffusion system|reaction-diffusion system]].<ref name=":0" /><ref name=":1" />
−
 
−
Pattern formation has been well studied in chemistry and chemical engineering, including both temperature and concentration patterns. The Brusselator model developed by Ilya Prigogine and collaborators is one such example that exhibits Turing instability. Pattern formation in chemical systems often involve oscillatory chemical kinetics or autocatalytic reactions such as Belousov–Zhabotinsky reaction or Briggs–Rauscher reaction. In industrial applications such as chemical reactors, pattern formation can lead to temperature hot spots which can reduce the yield or create hazardous safety problems such as a thermal runaway. The emergence of pattern formation can be studied by mathematical modeling and simulation of the underlying reaction-diffusion system.
 
−
 
−
模式的形成已经在化学和化学工程中得到了很好的研究，包括温度和浓度模式。由 Ilya Prigogine 和他的合作者发展的 Brusselator 模型就是这样一个展示图灵不稳定性的例子。化学体系中图形的形成通常涉及振荡化学动力学或自催化反应，如 Belousov-Zhabotinsky 反应或 Briggs-Rauscher 反应。在工业应用中，如化学反应堆，图案的形成可能导致温度热点，这可能降低产量或造成危险的安全问题，如热失控。模式形成的出现可以用潜在的反应扩散系统的数学建模与模拟来研究。
 
  
  
  
 +
Some types of automata have been used to generate organic-looking textures for more realistic shading of 3d objects.
  
 +
一些类型的自动机已经被用来生成看起来有机的纹理，以获得更加真实的三维物体着色。
  
 
* [[Belousov–Zhabotinsky reaction]]
 
* [[Belousov–Zhabotinsky reaction]]
−
 
−
 
  
 
* [[Liesegang rings]]
 
* [[Liesegang rings]]
  
 +
A popular Photoshop plugin, KPT 6, included a filter called 'KPT reaction'. Reaction produced reaction–diffusion style patterns based on the supplied seed image.
  
−
 
+
一个流行的 Photoshop 插件 KPT 6，包含了一个叫做 KPT reaction 的过滤器。基于提供的种子图像，反应产生反应扩散样式的图案。
−
 
 
  
  
第177行： 第115行：
 
===Physics===
 
===Physics===
  
−
===Physics===
+
A similar effect to the 'KPT reaction' can be achieved with convolution functions in digital image processing, with a little patience, by repeatedly sharpening and blurring an image in a graphics editor. If other filters are used, such as emboss or edge detection, different types of effects can be achieved.
  
−
物理学
+
在数字图像处理中，只需一点点耐心，通过在图形编辑器中反复锐化和模糊图像，就可以达到类似于“ KPT 反应”的效果。如果使用其他过滤器，如浮雕或边缘检测，可以实现不同类型的效果。
  
 
{{expand section|date=March 2013}}
 
{{expand section|date=March 2013}}
第185行： 第123行：
  
  
 +
Computers are often used to simulate the biological, physical or chemical processes that lead to pattern formation, and they can display the results in a realistic way. Calculations using models like reaction–diffusion or MClone are based on the actual mathematical equations designed by the scientists to model the studied phenomena.
  
−
 
+
计算机经常被用来模拟导致图案形成的生物、物理或化学过程，它们可以以一种逼真的方式显示结果。使用反应扩散或 MClone 等模型的计算是基于科学家为模拟所研究的现象而设计的实际数学方程。
−
 
 
  
 
In the 1980s [[Lugiato–Lefever equation|Lugiato and Lefever]] developed a model of light propagation in an optical cavity that results in pattern formation by the exploitation of nonlinear effects.
 
In the 1980s [[Lugiato–Lefever equation|Lugiato and Lefever]] developed a model of light propagation in an optical cavity that results in pattern formation by the exploitation of nonlinear effects.
−
 
−
In the 1980s Lugiato and Lefever developed a model of light propagation in an optical cavity that results in pattern formation by the exploitation of nonlinear effects.
 
−
 
−
在20世纪80年代，Lugiato 和 Lefever 发展了一个光在光学腔中传播的模型，该模型通过利用非线性效应形成图案。
 
−
 
−
 
  
  
  
 
[[Bénard cell]]s, [[laser]], [[cloud|cloud formation]]s in stripes or rolls. Ripples in icicles. Washboard patterns on dirtroads. [[dendrite (crystal)|Dendrites]] in [[freezing|solidification]], [[liquid crystal]]s. [[Soliton]]s.
 
[[Bénard cell]]s, [[laser]], [[cloud|cloud formation]]s in stripes or rolls. Ripples in icicles. Washboard patterns on dirtroads. [[dendrite (crystal)|Dendrites]] in [[freezing|solidification]], [[liquid crystal]]s. [[Soliton]]s.
−
 
−
Bénard cells, laser, cloud formations in stripes or rolls. Ripples in icicles. Washboard patterns on dirtroads. Dendrites in solidification, liquid crystals. Solitons.
 
−
 
−
B nard 细胞，激光，条纹或卷云的形成。冰柱上的涟漪。十字架上的搓板图案。凝固过程中的树枝晶、液晶。孤子。
 
−
 
−
 
−
 
  
  
−
===Mathematics===
 
  
 
===Mathematics===
 
===Mathematics===
−
 
−
数学
 
  
 
{{expand section|date=March 2013}}
 
{{expand section|date=March 2013}}
−
 
−
 
  
 
[[Sphere packing]]s and coverings. Mathematics underlies the other pattern formation mechanisms listed.
 
[[Sphere packing]]s and coverings. Mathematics underlies the other pattern formation mechanisms listed.
−
 
−
Sphere packings and coverings. Mathematics underlies the other pattern formation mechanisms listed.
 
−
 
−
球形填料和覆盖物。数学是其他模式形成机制的基础。
 
−
 
−
 
  
  
第232行： 第146行：
  
  
−
 
−
 
−
 
−
 
−
 
−
===Computer graphics===
 
  
 
===Computer graphics===
 
===Computer graphics===
−
 
−
计算机图形学
 
  
 
[[File:Homebrew reaction diffusion example 512iter.jpg|thumb|right|Pattern resembling a [[reaction–diffusion]] model, produced using sharpen and blur]]
 
[[File:Homebrew reaction diffusion example 512iter.jpg|thumb|right|Pattern resembling a [[reaction–diffusion]] model, produced using sharpen and blur]]
−
 
−
Pattern resembling a [[reaction–diffusion model, produced using sharpen and blur]]
 
−
 
−
图案类似于[[反应扩散模型，使用锐化和模糊]]
 
−
 
−
 
  
  
  
 
{{further|Cellular automaton}}
 
{{further|Cellular automaton}}
−
 
−
 
−
 
−
 
  
  
第263行： 第159行：
 
Some types of [[finite-state machine|automata]] have been used to generate organic-looking [[texture (computer graphics)|textures]] for more realistic [[Shader|shading]] of [[3D modeling|3d objects]].<ref>Greg Turk, [http://www.cc.gatech.edu/~turk/reaction_diffusion/reaction_diffusion.html Reaction–Diffusion]</ref><ref>{{cite journal|title=Reaction–Diffusion Textures|author1=Andrew Witkin |author2=Michael Kassy |url=https://www.cs.cmu.edu/~aw/pdf/texture.pdf|doi=10.1145/122718.122750|journal=Proceedings of the 18th Annual Conference on Computer Graphics and Interactive Techniques|year=1991|pages=299–308|isbn=0897914368 }}</ref>
 
Some types of [[finite-state machine|automata]] have been used to generate organic-looking [[texture (computer graphics)|textures]] for more realistic [[Shader|shading]] of [[3D modeling|3d objects]].<ref>Greg Turk, [http://www.cc.gatech.edu/~turk/reaction_diffusion/reaction_diffusion.html Reaction–Diffusion]</ref><ref>{{cite journal|title=Reaction–Diffusion Textures|author1=Andrew Witkin |author2=Michael Kassy |url=https://www.cs.cmu.edu/~aw/pdf/texture.pdf|doi=10.1145/122718.122750|journal=Proceedings of the 18th Annual Conference on Computer Graphics and Interactive Techniques|year=1991|pages=299–308|isbn=0897914368 }}</ref>
  
−
Some types of automata have been used to generate organic-looking textures for more realistic shading of 3d objects.
 
−
 
−
一些类型的自动机已经被用来生成看起来有机的纹理，以便对三维物体进行更真实的阴影处理。
 
−
 
−
 
−
 
−
 
−
 
−
A popular Photoshop plugin, [[Kai's Power Tools|KPT 6]], included a filter called 'KPT reaction'. Reaction produced [[reaction–diffusion system|reaction–diffusion]] style patterns based on the supplied seed image.
 
−
 
−
A popular Photoshop plugin, KPT 6, included a filter called 'KPT reaction'. Reaction produced reaction–diffusion style patterns based on the supplied seed image.
 
  
−
一个流行的 Photoshop 插件 KPT 6，包含了一个叫做 KPT reaction 的过滤器。基于提供的种子图像，反应产生反应扩散样式的图案。
 
−
 
−
 
−
 
−
 
−
 
−
A similar effect to the 'KPT reaction' can be achieved with [[convolution]] functions in [[digital image processing]], with a little patience, by repeatedly [[unsharp masking|sharpening]] and [[box blur|blurring]] an image in a graphics editor. If other filters are used, such as [[image embossing|emboss]] or [[edge detection]], different types of effects can be achieved.
 
−
 
−
A similar effect to the 'KPT reaction' can be achieved with convolution functions in digital image processing, with a little patience, by repeatedly sharpening and blurring an image in a graphics editor. If other filters are used, such as emboss or edge detection, different types of effects can be achieved.
 
−
 
−
在数字图像处理中，只需一点点耐心，通过在图形编辑器中反复锐化和模糊图像，就可以达到类似于“ KPT 反应”的效果。如果使用其他过滤器，如浮雕或边缘检测，可以实现不同类型的效果。
 
−
 
−
 
−
 
−
 
−
 
−
Computers are often used to [[computer simulation|simulate]] the biological, physical or chemical processes that lead to pattern formation, and they can display the results in a realistic way. Calculations using models like [[reaction–diffusion]] or [[MClone]] are based on the actual mathematical equations designed by the scientists to model the studied phenomena.
 
−
 
−
Computers are often used to simulate the biological, physical or chemical processes that lead to pattern formation, and they can display the results in a realistic way. Calculations using models like reaction–diffusion or MClone are based on the actual mathematical equations designed by the scientists to model the studied phenomena.
 
−
 
−
计算机经常被用来模拟导致图案形成的生物、物理或化学过程，它们可以以一种逼真的方式显示结果。使用反应扩散或 MClone 等模型的计算是基于科学家为模拟所研究的现象而设计的实际数学方程。
 
−
 
−
 
−
 
−
 
−
 
−
==References==
 
−
 
−
==References==
 
−
 
−
参考资料
 
−
 
−
{{reflist|30em}}
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
==Bibliography==
 
−
 
−
==Bibliography==
 
−
 
−
参考书目
 
−
 
−
* {{cite book|authorlink=Philip Ball|author=Ball, Philip|title=Nature's Patterns: a tapestry in three parts. 1:Shapes. 2:Flow. 3:Branches|publisher=Oxford|year=2009|isbn=978-0199604869}}
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
==External links==
 
−
 
−
==External links==
 
−
 
−
外部链接
 
−
 
−
* [https://web.archive.org/web/20190514060955/http://spiralzoom.com/Science/patternformation/patternformation.html ''SpiralZoom.com''], an educational website about the science of pattern formation, spirals in nature, and spirals in the mythic imagination.
 
−
 
−
 
−
 
−
* [https://books.google.com/books?id=T_i0o_55MNwC&printsec=frontcover&dq=introduction+to+computational+mathematics#v=onepage&q=pattern%20formation&f=false, '15-line Matlab code'], A simple 15-line Matlab program to simulate 2D pattern formation for reaction-diffusion model.
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
{{Patterns in nature}}
 
−
 
−
 
−
 
−
{{Genarch}}
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
{{DEFAULTSORT:Pattern Formation}}
 
−
 
−
 
−
 
−
[[Category:Developmental biology]]
 
  
 
Category:Developmental biology
 
Category:Developmental biology
第369行： 第165行：
 
类别: 发育生物学
 
类别: 发育生物学
  
−
[[Category:Articles containing video clips]]
+
A popular Photoshop plugin, [[Kai's Power Tools|KPT 6]], included a filter called 'KPT reaction'. Reaction produced [[reaction–diffusion system|reaction–diffusion]] style patterns based on the supplied seed image.
  
 
Category:Articles containing video clips
 
Category:Articles containing video clips
  
 
类别: 包含视频剪辑的文章
 
类别: 包含视频剪辑的文章
−
 
−
[[Category:Pattern formation]]
 
−
 
−
Category:Pattern formation
 
−
 
−
类别: 模式形成
 
  
 
<noinclude>
 
<noinclude>

2020年10月25日 (日) 17:51的版本

此词条暂由彩云小译翻译，翻译字数共484，未经人工整理和审校，带来阅读不便，请见谅。

Complex systems organizational map.jpg
Complex systems
Topics
文件:Self-organizing-Mechanism-for-Development-of-Space-filling-Neuronal-Dendrites-pcbi.0030212.sv003.ogv
Pattern formation in a computational model of dendrite growth.

Pattern formation in a computational model of dendrite growth.

在枝晶生长的计算模型中形成图案

The science of pattern formation deals with the visible, (statistically) orderly outcomes of self-organization and the common principles behind similar patterns in nature.

The science of pattern formation deals with the visible, (statistically) orderly outcomes of self-organization and the common principles behind similar patterns in nature.

模式形成的科学研究的是可见的、(统计学上)有序的自我组织和自然界中相似模式背后的共同原理。


In developmental biology, pattern formation refers to the generation of complex organizations of cell fates in space and time. Pattern formation is controlled by genes. The role of genes in pattern formation is an aspect of morphogenesis, the creation of diverse anatomies from similar genes, now being explored in the science of evolutionary developmental biology or evo-devo. The mechanisms involved are well seen in the anterior-posterior patterning of embryos from the model organism Drosophila melanogaster (a fruit fly), one of the first organisms to have its morphogenesis studied and in the eyespots of butterflies, whose development is a variant of the standard (fruit fly) mechanism.

In developmental biology, pattern formation refers to the generation of complex organizations of cell fates in space and time. Pattern formation is controlled by genes. The role of genes in pattern formation is an aspect of morphogenesis, the creation of diverse anatomies from similar genes, now being explored in the science of evolutionary developmental biology or evo-devo. The mechanisms involved are well seen in the anterior-posterior patterning of embryos from the model organism Drosophila melanogaster (a fruit fly), one of the first organisms to have its morphogenesis studied and in the eyespots of butterflies, whose development is a variant of the standard (fruit fly) mechanism.

在发育生物学，模式形成指的是细胞在空间和时间中命运的复杂组织的产生。模式的形成是由基因控制的。基因在模式形成中的作用是形态发生的一个方面，即从相似的基因中创造出不同的解剖结构，目前正在演化发育生物学科学或演化发育生物学中探索。模式生物黑腹果蝇(一种果蝇)的胚胎的前后部图案和蝴蝶的眼点都清楚地表明了其中的机制，前者是最早研究其形态发生的生物之一，后者的发育是标准(果蝇)机制的变体。


Examples

模板:Further

Examples of pattern formation can be found in biology, chemistry, physics, and mathematics,[1] and can readily be simulated with computer graphics, as described in turn below.

Examples of pattern formation can be found in biology, chemistry, physics, and mathematics, In contrast, fir waves occur in forests on mountain slopes after wind disturbance, during regeneration. When trees fall, the trees that they had sheltered become exposed and are in turn more likely to be damaged, so gaps tend to expand downwind. Meanwhile, on the windward side, young trees grow, protected by the wind shadow of the remaining tall trees. In flat terrains additional pattern morphologies appear besides stripes - hexagonal gap patterns and hexagonal spot patterns. Pattern formation in this case is driven by positive feedback loops between local vegetation growth and water transport towards the growth location. The emergence of pattern formation can be studied by mathematical modeling and simulation of the underlying reaction-diffusion system.

在生物学、化学、物理学和数学中都可以找到模式形成的例子。相反，在风扰动之后，在更新期间，冷杉波发生在山坡上的森林中。当树木倒下的时候，它们曾经庇护过的树木变得暴露，反过来更有可能受到损害，所以缝隙往往在下风处扩大。与此同时，在迎风面，年轻的树木生长，受到剩余高大树木的风影的保护。在平面地形中，除了条纹、六角形缝隙图案和六角形斑点图案外，还出现了其他图案形态。在这种情况下，格局的形成是由当地植被生长和水向生长地点输送之间的正反馈循环驱动的。模式形成的出现可以用潜在的反应扩散系统的数学建模与模拟来研究。


Biology

模板:Further


Biological patterns such as animal markings, the segmentation of animals, and phyllotaxis are formed in different ways.[2]


In developmental biology, pattern formation describes the mechanism by which initially equivalent cells in a developing tissue in an embryo assume complex forms and functions.[3] Embryogenesis, such as of the fruit fly Drosophila, involves coordinated control of cell fates.[4][5][6] Pattern formation is genetically controlled, and often involves each cell in a field sensing and responding to its position along a morphogen gradient, followed by short distance cell-to-cell communication through cell signaling pathways to refine the initial pattern. In this context, a field of cells is the group of cells whose fates are affected by responding to the same set positional information cues. This conceptual model was first described as the French flag model in the 1960s.[7][8] More generally, the morphology of organisms is patterned by the mechanisms of evolutionary developmental biology, such as changing the timing and positioning of specific developmental events in the embryo.[9]


In the 1980s Lugiato and Lefever developed a model of light propagation in an optical cavity that results in pattern formation by the exploitation of nonlinear effects.

在20世纪80年代，Lugiato 和 Lefever 发展了一个光在光学腔中传播的模型，这个模型通过利用非线性效应来形成图案。

Possible mechanisms of pattern formation in biological systems include the classical reaction–diffusion model proposed by Alan Turing[10] and the more recently found elastic instability mechanism which is thought to be responsible for the fold patterns on the cerebral cortex of higher animals, among other things.[11][12]


Bénard cells, laser, cloud formations in stripes or rolls. Ripples in icicles. Washboard patterns on dirtroads. Dendrites in solidification, liquid crystals. Solitons.

贝纳德细胞，激光，条纹或滚动的云层。冰柱上的涟漪。十字架上的搓板图案。凝固过程中的树枝晶、液晶。孤子。

Growth of colonies

Bacterial colonies show a large variety of patterns formed during colony growth. The resulting shapes depend on the growth conditions. In particular, stresses (hardness of the culture medium, lack of nutrients, etc.) enhance the complexity of the resulting patterns.[13] Other organisms such as slime moulds display remarkable patterns caused by the dynamics of chemical signaling.[14]


Vegetation patterns

Sphere packings and coverings. Mathematics underlies the other pattern formation mechanisms listed.

球形填料和覆盖物。数学是其他模式形成机制的基础。

Main article: patterned vegetation
Tiger bush is a vegetation pattern that forms in arid conditions.


Vegetation patterns such as tiger bush[15] and fir waves[16] form for different reasons. Tiger bush consists of stripes of bushes on arid slopes in countries such as Niger where plant growth is limited by rainfall. Each roughly horizontal stripe of vegetation absorbs rainwater from the bare zone immediately above it.[15] In contrast, fir waves occur in forests on mountain slopes after wind disturbance, during regeneration. When trees fall, the trees that they had sheltered become exposed and are in turn more likely to be damaged, so gaps tend to expand downwind. Meanwhile, on the windward side, young trees grow, protected by the wind shadow of the remaining tall trees.[16] In flat terrains additional pattern morphologies appear besides stripes - hexagonal gap patterns and hexagonal spot patterns. Pattern formation in this case is driven by positive feedback loops between local vegetation growth and water transport towards the growth location.[17][18]


Pattern resembling a reaction–diffusion model, produced using sharpen and blur

图案类似于反应扩散模型，使用锐化和模糊

Chemistry

模板:Expand section

模板:FurtherPattern formation has been well studied in chemistry and chemical engineering, including both temperature and concentration patterns.[19] The Brusselator model developed by Ilya Prigogine and collaborators is one such example that exhibits Turing instability.[20] Pattern formation in chemical systems often involve oscillatory chemical kinetics or autocatalytic reactions[21] such as Belousov–Zhabotinsky reaction or Briggs–Rauscher reaction. In industrial applications such as chemical reactors, pattern formation can lead to temperature hot spots which can reduce the yield or create hazardous safety problems such as a thermal runaway.[22][19] The emergence of pattern formation can be studied by mathematical modeling and simulation of the underlying reaction-diffusion system.[19][21]


Some types of automata have been used to generate organic-looking textures for more realistic shading of 3d objects.

一些类型的自动机已经被用来生成看起来有机的纹理，以获得更加真实的三维物体着色。

A popular Photoshop plugin, KPT 6, included a filter called 'KPT reaction'. Reaction produced reaction–diffusion style patterns based on the supplied seed image.

一个流行的 Photoshop 插件 KPT 6，包含了一个叫做 KPT reaction 的过滤器。基于提供的种子图像，反应产生反应扩散样式的图案。


Physics

A similar effect to the 'KPT reaction' can be achieved with convolution functions in digital image processing, with a little patience, by repeatedly sharpening and blurring an image in a graphics editor. If other filters are used, such as emboss or edge detection, different types of effects can be achieved.

在数字图像处理中，只需一点点耐心，通过在图形编辑器中反复锐化和模糊图像，就可以达到类似于“ KPT 反应”的效果。如果使用其他过滤器，如浮雕或边缘检测，可以实现不同类型的效果。

模板:Expand section


Computers are often used to simulate the biological, physical or chemical processes that lead to pattern formation, and they can display the results in a realistic way. Calculations using models like reaction–diffusion or MClone are based on the actual mathematical equations designed by the scientists to model the studied phenomena.

计算机经常被用来模拟导致图案形成的生物、物理或化学过程，它们可以以一种逼真的方式显示结果。使用反应扩散或 MClone 等模型的计算是基于科学家为模拟所研究的现象而设计的实际数学方程。

In the 1980s Lugiato and Lefever developed a model of light propagation in an optical cavity that results in pattern formation by the exploitation of nonlinear effects.


Bénard cells, laser, cloud formations in stripes or rolls. Ripples in icicles. Washboard patterns on dirtroads. Dendrites in solidification, liquid crystals. Solitons.


Mathematics

模板:Expand section

Sphere packings and coverings. Mathematics underlies the other pattern formation mechanisms listed.


模板:Further


Computer graphics

Pattern resembling a reaction–diffusion model, produced using sharpen and blur


模板:Further


Some types of automata have been used to generate organic-looking textures for more realistic shading of 3d objects.[23][24]


Category:Developmental biology

类别: 发育生物学

A popular Photoshop plugin, KPT 6, included a filter called 'KPT reaction'. Reaction produced reaction–diffusion style patterns based on the supplied seed image.

Category:Articles containing video clips

类别: 包含视频剪辑的文章


This page was moved from wikipedia:en:Pattern formation. Its edit history can be viewed at 斑图/edithistory

  1. ↑ Ball, 2009.
  2. ↑ Ball, 2009. Shapes, pp. 231–252.
  3. ↑ Ball, 2009. Shapes, pp. 261–290.
  4. ↑ Eric C. Lai (March 2004). "Notch signaling: control of cell communication and cell fate". Development. 131 (5): 965–73. doi:10.1242/dev.01074. PMID 14973298.
  5. ↑ Melinda J. Tyler, David A. Cameron (2007). "Cellular pattern formation during retinal regeneration: A role for homotypic control of cell fate acquisition". Vision Research. 47 (4): 501–511. doi:10.1016/j.visres.2006.08.025. PMID 17034830.{{cite journal}}: CS1 maint: uses authors parameter (link)
  6. ↑ Hans Meinhard (2001-10-26). "Biological pattern formation: How cell[s] talk with each other to achieve reproducible pattern formation". Max-Planck-Institut für Entwicklungsbiologie, Tübingen, Germany.
  7. ↑ Wolpert L (October 1969). "Positional information and the spatial pattern of cellular differentiation". J. Theor. Biol. 25 (1): 1–47. doi:10.1016/S0022-5193(69)80016-0. PMID 4390734.
  8. ↑ Wolpert, Lewis (2007). Principles of development (3rd ed.). Oxford [Oxfordshire]: Oxford University Press. ISBN 978-0-19-927536-6. 
  9. ↑ Hall, B. K. (2003). "Evo-Devo: evolutionary developmental mechanisms". International Journal of Developmental Biology. 47 (7–8): 491–495. PMID 14756324.
  10. ↑ S. Kondo, T. Miura, "Reaction-Diffusion Model as a Framework for Understanding Biological Pattern Formation", Science 24 Sep 2010: Vol. 329, Issue 5999, pp. 1616-1620 DOI: 10.1126/science.1179047
  11. ↑ Mercker, M; Brinkmann, F; Marciniak-Czochra, A; Richter, T (4 May 2016). "Beyond Turing: mechanochemical pattern formation in biological tissues". Biology Direct. 11: 22. doi:10.1186/s13062-016-0124-7. PMC 4857296. PMID 27145826.
  12. ↑ Tallinen et al. Nature Physics 12, 588–593 (2016) doi:10.1038/nphys3632
  13. ↑ Ball, 2009. Branches, pp. 52–59.
  14. ↑ Ball, 2009. Shapes, pp. 149–151.
  15. ↑ 15.0 15.1 Tongway, D.J., Valentin, C. & Seghieri, J. (2001). Banded vegetation patterning in arid and semiarid environments. New York: Springer-Verlag. ISBN 978-1461265597. 
  16. ↑ 16.0 16.1 D'Avanzo, C. (22 February 2004). "Fir Waves: Regeneration in New England Conifer Forests". TIEE. Retrieved 26 May 2012.
  17. ↑ Meron, E (2019). "Vegetation pattern formation: the mechanisms behind the forms". Physics Today. 72 (11): 30–36. doi:10.1063/PT.3.4340.
  18. ↑ Meron, E (2018). "From Patterns to Function in Living Systems: Dryland Ecosystems as a Case Study". Annual Review of Condensed Matter Physics. 9: 79–103. doi:10.1146/annurev-conmatphys-033117-053959.
  19. ↑ 19.0 19.1 19.2 Gupta, Ankur; Chakraborty, Saikat (January 2009). "Linear stability analysis of high- and low-dimensional models for describing mixing-limited pattern formation in homogeneous autocatalytic reactors". Chemical Engineering Journal. 145 (3): 399–411. doi:10.1016/j.cej.2008.08.025. ISSN 1385-8947.
  20. ↑ Prigogine, I.; Nicolis, G. (1985), Hazewinkel, M.; Jurkovich, R.; Paelinck, J. H. P. (eds.), "Self-Organisation in Nonequilibrium Systems: Towards A Dynamics of Complexity", Bifurcation Analysis: Principles, Applications and Synthesis, Springer Netherlands, pp. 3–12, doi:10.1007/978-94-009-6239-2_1, ISBN 9789400962392
  21. ↑ 21.0 21.1 Gupta, Ankur; Chakraborty, Saikat (2008-01-19). "Dynamic Simulation of Mixing-Limited Pattern Formation in Homogeneous Autocatalytic Reactions". Chemical Product and Process Modeling. 3 (2). doi:10.2202/1934-2659.1135. ISSN 1934-2659.
  22. ↑ Marwaha, Bharat; Sundarram, Sandhya; Luss, Dan (September 2004). "Dynamics of Transversal Hot Zones in Shallow Packed-Bed Reactors†". The Journal of Physical Chemistry B. 108 (38): 14470–14476. doi:10.1021/jp049803p. ISSN 1520-6106.
  23. ↑ Greg Turk, Reaction–Diffusion
  24. ↑ Andrew Witkin; Michael Kassy (1991). "Reaction–Diffusion Textures" (PDF). Proceedings of the 18th Annual Conference on Computer Graphics and Interactive Techniques: 299–308. doi:10.1145/122718.122750. ISBN 0897914368.
取自“https://wiki.swarma.org/index.php?title=斑图&oldid=16907”