“条件熵”的版本间的差异
小 (Moved page from wikipedia:en:Conditional entropy (history)) |
|||
| 第2行: | 第2行: | ||
{{Short description|Measure of relative information in probability theory}} | {{Short description|Measure of relative information in probability theory}} | ||
| − | |||
{{Information theory}} | {{Information theory}} | ||
| − | |||
| − | |||
[[Image:Entropy-mutual-information-relative-entropy-relation-diagram.svg|thumb|256px|right|[[Venn diagram]] showing additive and subtractive relationships various [[Quantities of information|information measures]] associated with correlated variables <math>X</math> and <math>Y</math>. The area contained by both circles is the [[joint entropy]] <math>\Eta(X,Y)</math>. The circle on the left (red and violet) is the [[Entropy (information theory)|individual entropy]] <math>\Eta(X)</math>, with the red being the [[conditional entropy]] <math>\Eta(X|Y)</math>. The circle on the right (blue and violet) is <math>\Eta(Y)</math>, with the blue being <math>\Eta(Y|X)</math>. The violet is the [[mutual information]] <math>\operatorname{I}(X;Y)</math>.]] | [[Image:Entropy-mutual-information-relative-entropy-relation-diagram.svg|thumb|256px|right|[[Venn diagram]] showing additive and subtractive relationships various [[Quantities of information|information measures]] associated with correlated variables <math>X</math> and <math>Y</math>. The area contained by both circles is the [[joint entropy]] <math>\Eta(X,Y)</math>. The circle on the left (red and violet) is the [[Entropy (information theory)|individual entropy]] <math>\Eta(X)</math>, with the red being the [[conditional entropy]] <math>\Eta(X|Y)</math>. The circle on the right (blue and violet) is <math>\Eta(Y)</math>, with the blue being <math>\Eta(Y|X)</math>. The violet is the [[mutual information]] <math>\operatorname{I}(X;Y)</math>.]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
In [[information theory]], the '''conditional entropy''' quantifies the amount of information needed to describe the outcome of a [[random variable]] <math>Y</math> given that the value of another random variable <math>X</math> is known. Here, information is measured in [[Shannon (unit)|shannon]]s, [[Nat (unit)|nat]]s, or [[Hartley (unit)|hartley]]s. The ''entropy of <math>Y</math> conditioned on <math>X</math>'' is written as <math>\Eta(Y|X)</math>. | In [[information theory]], the '''conditional entropy''' quantifies the amount of information needed to describe the outcome of a [[random variable]] <math>Y</math> given that the value of another random variable <math>X</math> is known. Here, information is measured in [[Shannon (unit)|shannon]]s, [[Nat (unit)|nat]]s, or [[Hartley (unit)|hartley]]s. The ''entropy of <math>Y</math> conditioned on <math>X</math>'' is written as <math>\Eta(Y|X)</math>. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Definition == | == Definition == | ||
| − | |||
The conditional entropy of <math>Y</math> given <math>X</math> is defined as | The conditional entropy of <math>Y</math> given <math>X</math> is defined as | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{Equation box 1 | {{Equation box 1 | ||
| − | |||
| − | |||
| − | |||
|indent = | |indent = | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|title= | |title= | ||
| − | |||
| − | |||
| − | |||
|equation = {{NumBlk||<math>\Eta(Y|X)\ = -\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log \frac {p(x,y)} {p(x)}</math>|{{EquationRef|Eq.1}}}} | |equation = {{NumBlk||<math>\Eta(Y|X)\ = -\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log \frac {p(x,y)} {p(x)}</math>|{{EquationRef|Eq.1}}}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|cellpadding= 6 | |cellpadding= 6 | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|border | |border | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|border colour = #0073CF | |border colour = #0073CF | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|background colour=#F5FFFA}} | |background colour=#F5FFFA}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
where <math>\mathcal X</math> and <math>\mathcal Y</math> denote the [[Support (mathematics)|support sets]] of <math>X</math> and <math>Y</math>. | where <math>\mathcal X</math> and <math>\mathcal Y</math> denote the [[Support (mathematics)|support sets]] of <math>X</math> and <math>Y</math>. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
''Note:'' It is conventioned that the expressions <math>0 \log 0</math> and <math>0 \log c/0</math> for fixed <math>c > 0</math> should be treated as being equal to zero. This is because <math>\lim_{\theta\to0^+} \theta\, \log \,c/\theta = 0</math> and <math>\lim_{\theta\to0^+} \theta\, \log \theta = 0</math><ref>{{Cite web|url=http://www.inference.org.uk/mackay/itprnn/book.html|title=David MacKay: Information Theory, Pattern Recognition and Neural Networks: The Book|website=www.inference.org.uk|access-date=2019-10-25}}</ref> <!-- because p(x,y) could still equal 0 even if p(x) != 0 and p(y) != 0. What about p(x,y)=p(x)=0? --> | ''Note:'' It is conventioned that the expressions <math>0 \log 0</math> and <math>0 \log c/0</math> for fixed <math>c > 0</math> should be treated as being equal to zero. This is because <math>\lim_{\theta\to0^+} \theta\, \log \,c/\theta = 0</math> and <math>\lim_{\theta\to0^+} \theta\, \log \theta = 0</math><ref>{{Cite web|url=http://www.inference.org.uk/mackay/itprnn/book.html|title=David MacKay: Information Theory, Pattern Recognition and Neural Networks: The Book|website=www.inference.org.uk|access-date=2019-10-25}}</ref> <!-- because p(x,y) could still equal 0 even if p(x) != 0 and p(y) != 0. What about p(x,y)=p(x)=0? --> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Intuitive explanation of the definition : | Intuitive explanation of the definition : | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
According to the definition, <math>\displaystyle H( Y|X) =\mathbb{E}( \ f( X,Y) \ )</math> where <math>\displaystyle f:( x,y) \ \rightarrow -\log( \ p( y|x) \ ) .</math> <math>\displaystyle f</math> associates to <math>\displaystyle ( x,y)</math> the information content of <math>\displaystyle ( Y=y)</math> given <math>\displaystyle (X=x)</math>, which is the amount of information needed to describe the event <math>\displaystyle (Y=y)</math> given <math>(X=x)</math>. According to the law of large numbers, <math>\displaystyle H(Y|X)</math> is the arithmetic mean of a large number of independent realizations of <math>\displaystyle f(X,Y)</math>. | According to the definition, <math>\displaystyle H( Y|X) =\mathbb{E}( \ f( X,Y) \ )</math> where <math>\displaystyle f:( x,y) \ \rightarrow -\log( \ p( y|x) \ ) .</math> <math>\displaystyle f</math> associates to <math>\displaystyle ( x,y)</math> the information content of <math>\displaystyle ( Y=y)</math> given <math>\displaystyle (X=x)</math>, which is the amount of information needed to describe the event <math>\displaystyle (Y=y)</math> given <math>(X=x)</math>. According to the law of large numbers, <math>\displaystyle H(Y|X)</math> is the arithmetic mean of a large number of independent realizations of <math>\displaystyle f(X,Y)</math>. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Motivation == | == Motivation == | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Let <math>\Eta(Y|X=x)</math> be the [[Shannon Entropy|entropy]] of the discrete random variable <math>Y</math> conditioned on the discrete random variable <math>X</math> taking a certain value <math>x</math>. Denote the support sets of <math>X</math> and <math>Y</math> by <math>\mathcal X</math> and <math>\mathcal Y</math>. Let <math>Y</math> have [[probability mass function]] <math>p_Y{(y)}</math>. The unconditional entropy of <math>Y</math> is calculated as <math>\Eta(Y) := \mathbb{E}[\operatorname{I}(Y)]</math>, i.e. | Let <math>\Eta(Y|X=x)</math> be the [[Shannon Entropy|entropy]] of the discrete random variable <math>Y</math> conditioned on the discrete random variable <math>X</math> taking a certain value <math>x</math>. Denote the support sets of <math>X</math> and <math>Y</math> by <math>\mathcal X</math> and <math>\mathcal Y</math>. Let <math>Y</math> have [[probability mass function]] <math>p_Y{(y)}</math>. The unconditional entropy of <math>Y</math> is calculated as <math>\Eta(Y) := \mathbb{E}[\operatorname{I}(Y)]</math>, i.e. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
:<math>\Eta(Y) = \sum_{y\in\mathcal Y} {\mathrm{Pr}(Y=y)\,\mathrm{I}(y)} | :<math>\Eta(Y) = \sum_{y\in\mathcal Y} {\mathrm{Pr}(Y=y)\,\mathrm{I}(y)} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
= -\sum_{y\in\mathcal Y} {p_Y(y) \log_2{p_Y(y)}},</math> | = -\sum_{y\in\mathcal Y} {p_Y(y) \log_2{p_Y(y)}},</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
where <math>\operatorname{I}(y_i)</math> is the [[information content]] of the [[Outcome (probability)|outcome]] of <math>Y</math> taking the value <math>y_i</math>. The entropy of <math>Y</math> conditioned on <math>X</math> taking the value <math>x</math> is defined analogously by [[conditional expectation]]: | where <math>\operatorname{I}(y_i)</math> is the [[information content]] of the [[Outcome (probability)|outcome]] of <math>Y</math> taking the value <math>y_i</math>. The entropy of <math>Y</math> conditioned on <math>X</math> taking the value <math>x</math> is defined analogously by [[conditional expectation]]: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
:<math>\Eta(Y|X=x) | :<math>\Eta(Y|X=x) | ||
| − | |||
= -\sum_{y\in\mathcal Y} {\Pr(Y = y|X=x) \log_2{\Pr(Y = y|X=x)}}.</math> | = -\sum_{y\in\mathcal Y} {\Pr(Y = y|X=x) \log_2{\Pr(Y = y|X=x)}}.</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Note that <math>\Eta(Y|X)</math> is the result of averaging <math>\Eta(Y|X=x)</math> over all possible values <math>x</math> that <math>X</math> may take. Also, if the above sum is taken over a sample <math>y_1, \dots, y_n</math>, the expected value <math>E_X[ \Eta(y_1, \dots, y_n \mid X = x)]</math> is known in some domains as '''equivocation'''.<ref>{{cite journal|author1=Hellman, M.|author2=Raviv, J.|year=1970|title=Probability of error, equivocation, and the Chernoff bound|journal=IEEE Transactions on Information Theory|volume=16|issue=4|pp=368-372}}</ref> | Note that <math>\Eta(Y|X)</math> is the result of averaging <math>\Eta(Y|X=x)</math> over all possible values <math>x</math> that <math>X</math> may take. Also, if the above sum is taken over a sample <math>y_1, \dots, y_n</math>, the expected value <math>E_X[ \Eta(y_1, \dots, y_n \mid X = x)]</math> is known in some domains as '''equivocation'''.<ref>{{cite journal|author1=Hellman, M.|author2=Raviv, J.|year=1970|title=Probability of error, equivocation, and the Chernoff bound|journal=IEEE Transactions on Information Theory|volume=16|issue=4|pp=368-372}}</ref> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Given [[Discrete random variable|discrete random variables]] <math>X</math> with image <math>\mathcal X</math> and <math>Y</math> with image <math>\mathcal Y</math>, the conditional entropy of <math>Y</math> given <math>X</math> is defined as the weighted sum of <math>\Eta(Y|X=x)</math> for each possible value of <math>x</math>, using <math>p(x)</math> as the weights:<ref name=cover1991>{{cite book|isbn=0-471-06259-6|year=1991|authorlink1=Thomas M. Cover|author1=T. Cover|author2=J. Thomas|title=Elements of Information Theory|url=https://archive.org/details/elementsofinform0000cove|url-access=registration}}</ref>{{rp|15}} | Given [[Discrete random variable|discrete random variables]] <math>X</math> with image <math>\mathcal X</math> and <math>Y</math> with image <math>\mathcal Y</math>, the conditional entropy of <math>Y</math> given <math>X</math> is defined as the weighted sum of <math>\Eta(Y|X=x)</math> for each possible value of <math>x</math>, using <math>p(x)</math> as the weights:<ref name=cover1991>{{cite book|isbn=0-471-06259-6|year=1991|authorlink1=Thomas M. Cover|author1=T. Cover|author2=J. Thomas|title=Elements of Information Theory|url=https://archive.org/details/elementsofinform0000cove|url-access=registration}}</ref>{{rp|15}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
:<math> | :<math> | ||
| − | |||
\begin{align} | \begin{align} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
\Eta(Y|X)\ &\equiv \sum_{x\in\mathcal X}\,p(x)\,\Eta(Y|X=x)\\ | \Eta(Y|X)\ &\equiv \sum_{x\in\mathcal X}\,p(x)\,\Eta(Y|X=x)\\ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
& =-\sum_{x\in\mathcal X} p(x)\sum_{y\in\mathcal Y}\,p(y|x)\,\log\, p(y|x)\\ | & =-\sum_{x\in\mathcal X} p(x)\sum_{y\in\mathcal Y}\,p(y|x)\,\log\, p(y|x)\\ | ||
| − | |||
& =-\sum_{x\in\mathcal X}\sum_{y\in\mathcal Y}\,p(x,y)\,\log\,p(y|x)\\ | & =-\sum_{x\in\mathcal X}\sum_{y\in\mathcal Y}\,p(x,y)\,\log\,p(y|x)\\ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
& =-\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log\,p(y|x)\\ | & =-\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log\,p(y|x)\\ | ||
| − | |||
& =-\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log \frac {p(x,y)} {p(x)}. \\ | & =-\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log \frac {p(x,y)} {p(x)}. \\ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
& = \sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log \frac {p(x)} {p(x,y)}. \\ | & = \sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log \frac {p(x)} {p(x,y)}. \\ | ||
| − | |||
\end{align} | \end{align} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</math> | </math> | ||
| − | |||
| − | |||
<!-- This paragraph is incorrect; the last line is not the KL divergence between any two distributions, since p(x) is [in general] not a valid distribution over the domains of X and Y. The last formula above is the [[Kullback-Leibler divergence]], also known as relative entropy. Relative entropy is always positive, and vanishes if and only if <math>p(x,y) = p(x)</math>. This is when knowing <math>x</math> tells us everything about <math>y</math>. ADDED: Could this comment be out of date since the KL divergence is not mentioned above? November 2014 --> | <!-- This paragraph is incorrect; the last line is not the KL divergence between any two distributions, since p(x) is [in general] not a valid distribution over the domains of X and Y. The last formula above is the [[Kullback-Leibler divergence]], also known as relative entropy. Relative entropy is always positive, and vanishes if and only if <math>p(x,y) = p(x)</math>. This is when knowing <math>x</math> tells us everything about <math>y</math>. ADDED: Could this comment be out of date since the KL divergence is not mentioned above? November 2014 --> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Properties== | ==Properties== | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===Conditional entropy equals zero=== | ===Conditional entropy equals zero=== | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<math>\Eta(Y|X)=0</math> if and only if the value of <math>Y</math> is completely determined by the value of <math>X</math>. | <math>\Eta(Y|X)=0</math> if and only if the value of <math>Y</math> is completely determined by the value of <math>X</math>. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===Conditional entropy of independent random variables=== | ===Conditional entropy of independent random variables=== | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Conversely, <math>\Eta(Y|X) = \Eta(Y)</math> if and only if <math>Y</math> and <math>X</math> are [[independent random variables]]. | Conversely, <math>\Eta(Y|X) = \Eta(Y)</math> if and only if <math>Y</math> and <math>X</math> are [[independent random variables]]. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===Chain rule=== | ===Chain rule=== | ||
| − | |||
Assume that the combined system determined by two random variables <math>X</math> and <math>Y</math> has [[joint entropy]] <math>\Eta(X,Y)</math>, that is, we need <math>\Eta(X,Y)</math> bits of information on average to describe its exact state. Now if we first learn the value of <math>X</math>, we have gained <math>\Eta(X)</math> bits of information. Once <math>X</math> is known, we only need <math>\Eta(X,Y)-\Eta(X)</math> bits to describe the state of the whole system. This quantity is exactly <math>\Eta(Y|X)</math>, which gives the ''chain rule'' of conditional entropy: | Assume that the combined system determined by two random variables <math>X</math> and <math>Y</math> has [[joint entropy]] <math>\Eta(X,Y)</math>, that is, we need <math>\Eta(X,Y)</math> bits of information on average to describe its exact state. Now if we first learn the value of <math>X</math>, we have gained <math>\Eta(X)</math> bits of information. Once <math>X</math> is known, we only need <math>\Eta(X,Y)-\Eta(X)</math> bits to describe the state of the whole system. This quantity is exactly <math>\Eta(Y|X)</math>, which gives the ''chain rule'' of conditional entropy: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
:<math>\Eta(Y|X)\, = \, \Eta(X,Y)- \Eta(X).</math><ref name=cover1991 />{{rp|17}} | :<math>\Eta(Y|X)\, = \, \Eta(X,Y)- \Eta(X).</math><ref name=cover1991 />{{rp|17}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
The chain rule follows from the above definition of conditional entropy: | The chain rule follows from the above definition of conditional entropy: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
:<math>\begin{align} | :<math>\begin{align} | ||
| − | |||
\Eta(Y|X) &= \sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log \left(\frac{p(x)}{p(x,y)} \right) \\[4pt] | \Eta(Y|X) &= \sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log \left(\frac{p(x)}{p(x,y)} \right) \\[4pt] | ||
| − | |||
&= \sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)(\log (p(x))-\log (p(x,y))) \\[4pt] | &= \sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)(\log (p(x))-\log (p(x,y))) \\[4pt] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
&= -\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log (p(x,y)) + \sum_{x\in\mathcal X, y\in\mathcal Y}{p(x,y)\log(p(x))} \\[4pt] | &= -\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log (p(x,y)) + \sum_{x\in\mathcal X, y\in\mathcal Y}{p(x,y)\log(p(x))} \\[4pt] | ||
| − | |||
& = \Eta(X,Y) + \sum_{x \in \mathcal X} p(x)\log (p(x) ) \\[4pt] | & = \Eta(X,Y) + \sum_{x \in \mathcal X} p(x)\log (p(x) ) \\[4pt] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
& = \Eta(X,Y) - \Eta(X). | & = \Eta(X,Y) - \Eta(X). | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
\end{align}</math> | \end{align}</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
In general, a chain rule for multiple random variables holds: | In general, a chain rule for multiple random variables holds: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
:<math> \Eta(X_1,X_2,\ldots,X_n) = | :<math> \Eta(X_1,X_2,\ldots,X_n) = | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
\sum_{i=1}^n \Eta(X_i | X_1, \ldots, X_{i-1}) </math><ref name=cover1991 />{{rp|22}} | \sum_{i=1}^n \Eta(X_i | X_1, \ldots, X_{i-1}) </math><ref name=cover1991 />{{rp|22}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
It has a similar form to [[Chain rule (probability)|chain rule]] in probability theory, except that addition instead of multiplication is used. | It has a similar form to [[Chain rule (probability)|chain rule]] in probability theory, except that addition instead of multiplication is used. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===Bayes' rule=== | ===Bayes' rule=== | ||
| − | |||
[[Bayes' rule]] for conditional entropy states | [[Bayes' rule]] for conditional entropy states | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
:<math>\Eta(Y|X) \,=\, \Eta(X|Y) - \Eta(X) + \Eta(Y).</math> | :<math>\Eta(Y|X) \,=\, \Eta(X|Y) - \Eta(X) + \Eta(Y).</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
''Proof.'' <math>\Eta(Y|X) = \Eta(X,Y) - \Eta(X)</math> and <math>\Eta(X|Y) = \Eta(Y,X) - \Eta(Y)</math>. Symmetry entails <math>\Eta(X,Y) = \Eta(Y,X)</math>. Subtracting the two equations implies Bayes' rule. | ''Proof.'' <math>\Eta(Y|X) = \Eta(X,Y) - \Eta(X)</math> and <math>\Eta(X|Y) = \Eta(Y,X) - \Eta(Y)</math>. Symmetry entails <math>\Eta(X,Y) = \Eta(Y,X)</math>. Subtracting the two equations implies Bayes' rule. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
If <math>Y</math> is [[Conditional independence|conditionally independent]] of <math>Z</math> given <math>X</math> we have: | If <math>Y</math> is [[Conditional independence|conditionally independent]] of <math>Z</math> given <math>X</math> we have: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
:<math>\Eta(Y|X,Z) \,=\, \Eta(Y|X).</math> | :<math>\Eta(Y|X,Z) \,=\, \Eta(Y|X).</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===Other properties=== | ===Other properties=== | ||
| − | |||
For any <math>X</math> and <math>Y</math>: | For any <math>X</math> and <math>Y</math>: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
:<math display="block">\begin{align} | :<math display="block">\begin{align} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
\Eta(Y|X) &\le \Eta(Y) \, \\ | \Eta(Y|X) &\le \Eta(Y) \, \\ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
\Eta(X,Y) &= \Eta(X|Y) + \Eta(Y|X) + \operatorname{I}(X;Y),\qquad \\ | \Eta(X,Y) &= \Eta(X|Y) + \Eta(Y|X) + \operatorname{I}(X;Y),\qquad \\ | ||
| − | |||
\Eta(X,Y) &= \Eta(X) + \Eta(Y) - \operatorname{I}(X;Y),\, \\ | \Eta(X,Y) &= \Eta(X) + \Eta(Y) - \operatorname{I}(X;Y),\, \\ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
\operatorname{I}(X;Y) &\le \Eta(X),\, | \operatorname{I}(X;Y) &\le \Eta(X),\, | ||
| − | |||
\end{align}</math> | \end{align}</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
where <math>\operatorname{I}(X;Y)</math> is the [[mutual information]] between <math>X</math> and <math>Y</math>. | where <math>\operatorname{I}(X;Y)</math> is the [[mutual information]] between <math>X</math> and <math>Y</math>. | ||
| − | |||
| − | |||
For independent <math>X</math> and <math>Y</math>: | For independent <math>X</math> and <math>Y</math>: | ||
| − | |||
| − | |||
:<math>\Eta(Y|X) = \Eta(Y) </math> and <math>\Eta(X|Y) = \Eta(X) \, </math> | :<math>\Eta(Y|X) = \Eta(Y) </math> and <math>\Eta(X|Y) = \Eta(X) \, </math> | ||
| − | |||
| − | |||
Although the specific-conditional entropy <math>\Eta(X|Y=y)</math> can be either less or greater than <math>\Eta(X)</math> for a given [[random variate]] <math>y</math> of <math>Y</math>, <math>\Eta(X|Y)</math> can never exceed <math>\Eta(X)</math>. | Although the specific-conditional entropy <math>\Eta(X|Y=y)</math> can be either less or greater than <math>\Eta(X)</math> for a given [[random variate]] <math>y</math> of <math>Y</math>, <math>\Eta(X|Y)</math> can never exceed <math>\Eta(X)</math>. | ||
| − | |||
| − | |||
== Conditional differential entropy == | == Conditional differential entropy == | ||
| − | |||
=== Definition === | === Definition === | ||
| − | |||
The above definition is for discrete random variables. The continuous version of discrete conditional entropy is called ''conditional differential (or continuous) entropy''. Let <math>X</math> and <math>Y</math> be a continuous random variables with a [[joint probability density function]] <math>f(x,y)</math>. The differential conditional entropy <math>h(X|Y)</math> is defined as<ref name=cover1991 />{{rp|249}} | The above definition is for discrete random variables. The continuous version of discrete conditional entropy is called ''conditional differential (or continuous) entropy''. Let <math>X</math> and <math>Y</math> be a continuous random variables with a [[joint probability density function]] <math>f(x,y)</math>. The differential conditional entropy <math>h(X|Y)</math> is defined as<ref name=cover1991 />{{rp|249}} | ||
| + | {{Equation box 1 | ||
| + | |indent = | ||
| + | |title= | ||
| + | |equation = {{NumBlk||<math>h(X|Y) = -\int_{\mathcal X, \mathcal Y} f(x,y)\log f(x|y)\,dx dy</math>|{{EquationRef|Eq.2}}}} | ||
| + | |cellpadding= 6 | ||
| + | |border | ||
| + | |border colour = #0073CF | ||
| + | |background colour=#F5FFFA}} | ||
| + | === Properties === | ||
| + | In contrast to the conditional entropy for discrete random variables, the conditional differential entropy may be negative. | ||
| − | {{ | + | As in the discrete case there is a chain rule for differential entropy: |
| + | :<math>h(Y|X)\,=\,h(X,Y)-h(X)</math><ref name=cover1991 />{{rp|253}} | ||
| + | Notice however that this rule may not be true if the involved differential entropies do not exist or are infinite. | ||
| − | + | Joint differential entropy is also used in the definition of the [[mutual information]] between continuous random variables: | |
| + | :<math>\operatorname{I}(X,Y)=h(X)-h(X|Y)=h(Y)-h(Y|X)</math> | ||
| − | + | <math>h(X|Y) \le h(X)</math> with equality if and only if <math>X</math> and <math>Y</math> are independent.<ref name=cover1991 />{{rp|253}} | |
| − | | | + | ===Relation to estimator error=== |
| + | The conditional differential entropy yields a lower bound on the expected squared error of an [[estimator]]. For any random variable <math>X</math>, observation <math>Y</math> and estimator <math>\widehat{X}</math> the following holds:<ref name=cover1991 />{{rp|255}} | ||
| + | :<math display="block">\mathbb{E}\left[\bigl(X - \widehat{X}{(Y)}\bigr)^2\right] | ||
| + | \ge \frac{1}{2\pi e}e^{2h(X|Y)}</math> | ||
| − | + | This is related to the [[uncertainty principle]] from [[quantum mechanics]]. | |
| − | + | ==Generalization to quantum theory== | |
| + | In [[quantum information theory]], the conditional entropy is generalized to the [[conditional quantum entropy]]. The latter can take negative values, unlike its classical counterpart. | ||
| − | + | == See also == | |
| + | * [[Entropy (information theory)]] | ||
| + | * [[Mutual information]] | ||
| + | * [[Conditional quantum entropy]] | ||
| + | * [[Variation of information]] | ||
| + | * [[Entropy power inequality]] | ||
| + | * [[Likelihood function]] | ||
| − | + | ==References== | |
| + | {{Reflist}} | ||
| − | [[Category: | + | [[Category:Entropy and information]] |
| + | [[Category:Information theory]] | ||
2020年10月26日 (一) 09:42的版本
此词条暂由彩云小译翻译,未经人工整理和审校,带来阅读不便,请见谅。
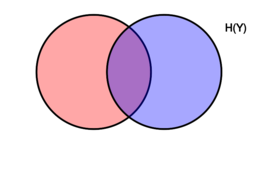
In information theory, the conditional entropy quantifies the amount of information needed to describe the outcome of a random variable [math]\displaystyle{ Y }[/math] given that the value of another random variable [math]\displaystyle{ X }[/math] is known. Here, information is measured in shannons, nats, or hartleys. The entropy of [math]\displaystyle{ Y }[/math] conditioned on [math]\displaystyle{ X }[/math] is written as [math]\displaystyle{ \Eta(Y|X) }[/math].
Definition
The conditional entropy of [math]\displaystyle{ Y }[/math] given [math]\displaystyle{ X }[/math] is defined as
[math]\displaystyle{ \Eta(Y|X)\ = -\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log \frac {p(x,y)} {p(x)} }[/math]
|
|
(Eq.1) |
where [math]\displaystyle{ \mathcal X }[/math] and [math]\displaystyle{ \mathcal Y }[/math] denote the support sets of [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math].
Note: It is conventioned that the expressions [math]\displaystyle{ 0 \log 0 }[/math] and [math]\displaystyle{ 0 \log c/0 }[/math] for fixed [math]\displaystyle{ c \gt 0 }[/math] should be treated as being equal to zero. This is because [math]\displaystyle{ \lim_{\theta\to0^+} \theta\, \log \,c/\theta = 0 }[/math] and [math]\displaystyle{ \lim_{\theta\to0^+} \theta\, \log \theta = 0 }[/math][1]
Intuitive explanation of the definition : According to the definition, [math]\displaystyle{ \displaystyle H( Y|X) =\mathbb{E}( \ f( X,Y) \ ) }[/math] where [math]\displaystyle{ \displaystyle f:( x,y) \ \rightarrow -\log( \ p( y|x) \ ) . }[/math] [math]\displaystyle{ \displaystyle f }[/math] associates to [math]\displaystyle{ \displaystyle ( x,y) }[/math] the information content of [math]\displaystyle{ \displaystyle ( Y=y) }[/math] given [math]\displaystyle{ \displaystyle (X=x) }[/math], which is the amount of information needed to describe the event [math]\displaystyle{ \displaystyle (Y=y) }[/math] given [math]\displaystyle{ (X=x) }[/math]. According to the law of large numbers, [math]\displaystyle{ \displaystyle H(Y|X) }[/math] is the arithmetic mean of a large number of independent realizations of [math]\displaystyle{ \displaystyle f(X,Y) }[/math].
Motivation
Let [math]\displaystyle{ \Eta(Y|X=x) }[/math] be the entropy of the discrete random variable [math]\displaystyle{ Y }[/math] conditioned on the discrete random variable [math]\displaystyle{ X }[/math] taking a certain value [math]\displaystyle{ x }[/math]. Denote the support sets of [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] by [math]\displaystyle{ \mathcal X }[/math] and [math]\displaystyle{ \mathcal Y }[/math]. Let [math]\displaystyle{ Y }[/math] have probability mass function [math]\displaystyle{ p_Y{(y)} }[/math]. The unconditional entropy of [math]\displaystyle{ Y }[/math] is calculated as [math]\displaystyle{ \Eta(Y) := \mathbb{E}[\operatorname{I}(Y)] }[/math], i.e.
- [math]\displaystyle{ \Eta(Y) = \sum_{y\in\mathcal Y} {\mathrm{Pr}(Y=y)\,\mathrm{I}(y)} = -\sum_{y\in\mathcal Y} {p_Y(y) \log_2{p_Y(y)}}, }[/math]
where [math]\displaystyle{ \operatorname{I}(y_i) }[/math] is the information content of the outcome of [math]\displaystyle{ Y }[/math] taking the value [math]\displaystyle{ y_i }[/math]. The entropy of [math]\displaystyle{ Y }[/math] conditioned on [math]\displaystyle{ X }[/math] taking the value [math]\displaystyle{ x }[/math] is defined analogously by conditional expectation:
- [math]\displaystyle{ \Eta(Y|X=x) = -\sum_{y\in\mathcal Y} {\Pr(Y = y|X=x) \log_2{\Pr(Y = y|X=x)}}. }[/math]
Note that [math]\displaystyle{ \Eta(Y|X) }[/math] is the result of averaging [math]\displaystyle{ \Eta(Y|X=x) }[/math] over all possible values [math]\displaystyle{ x }[/math] that [math]\displaystyle{ X }[/math] may take. Also, if the above sum is taken over a sample [math]\displaystyle{ y_1, \dots, y_n }[/math], the expected value [math]\displaystyle{ E_X[ \Eta(y_1, \dots, y_n \mid X = x)] }[/math] is known in some domains as equivocation.[2]
Given discrete random variables [math]\displaystyle{ X }[/math] with image [math]\displaystyle{ \mathcal X }[/math] and [math]\displaystyle{ Y }[/math] with image [math]\displaystyle{ \mathcal Y }[/math], the conditional entropy of [math]\displaystyle{ Y }[/math] given [math]\displaystyle{ X }[/math] is defined as the weighted sum of [math]\displaystyle{ \Eta(Y|X=x) }[/math] for each possible value of [math]\displaystyle{ x }[/math], using [math]\displaystyle{ p(x) }[/math] as the weights:[3]:15
- [math]\displaystyle{ \begin{align} \Eta(Y|X)\ &\equiv \sum_{x\in\mathcal X}\,p(x)\,\Eta(Y|X=x)\\ & =-\sum_{x\in\mathcal X} p(x)\sum_{y\in\mathcal Y}\,p(y|x)\,\log\, p(y|x)\\ & =-\sum_{x\in\mathcal X}\sum_{y\in\mathcal Y}\,p(x,y)\,\log\,p(y|x)\\ & =-\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log\,p(y|x)\\ & =-\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log \frac {p(x,y)} {p(x)}. \\ & = \sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log \frac {p(x)} {p(x,y)}. \\ \end{align} }[/math]
Properties
Conditional entropy equals zero
[math]\displaystyle{ \Eta(Y|X)=0 }[/math] if and only if the value of [math]\displaystyle{ Y }[/math] is completely determined by the value of [math]\displaystyle{ X }[/math].
Conditional entropy of independent random variables
Conversely, [math]\displaystyle{ \Eta(Y|X) = \Eta(Y) }[/math] if and only if [math]\displaystyle{ Y }[/math] and [math]\displaystyle{ X }[/math] are independent random variables.
Chain rule
Assume that the combined system determined by two random variables [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] has joint entropy [math]\displaystyle{ \Eta(X,Y) }[/math], that is, we need [math]\displaystyle{ \Eta(X,Y) }[/math] bits of information on average to describe its exact state. Now if we first learn the value of [math]\displaystyle{ X }[/math], we have gained [math]\displaystyle{ \Eta(X) }[/math] bits of information. Once [math]\displaystyle{ X }[/math] is known, we only need [math]\displaystyle{ \Eta(X,Y)-\Eta(X) }[/math] bits to describe the state of the whole system. This quantity is exactly [math]\displaystyle{ \Eta(Y|X) }[/math], which gives the chain rule of conditional entropy:
- [math]\displaystyle{ \Eta(Y|X)\, = \, \Eta(X,Y)- \Eta(X). }[/math][3]:17
The chain rule follows from the above definition of conditional entropy:
- [math]\displaystyle{ \begin{align} \Eta(Y|X) &= \sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log \left(\frac{p(x)}{p(x,y)} \right) \\[4pt] &= \sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)(\log (p(x))-\log (p(x,y))) \\[4pt] &= -\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log (p(x,y)) + \sum_{x\in\mathcal X, y\in\mathcal Y}{p(x,y)\log(p(x))} \\[4pt] & = \Eta(X,Y) + \sum_{x \in \mathcal X} p(x)\log (p(x) ) \\[4pt] & = \Eta(X,Y) - \Eta(X). \end{align} }[/math]
In general, a chain rule for multiple random variables holds:
- [math]\displaystyle{ \Eta(X_1,X_2,\ldots,X_n) = \sum_{i=1}^n \Eta(X_i | X_1, \ldots, X_{i-1}) }[/math][3]:22
It has a similar form to chain rule in probability theory, except that addition instead of multiplication is used.
Bayes' rule
Bayes' rule for conditional entropy states
- [math]\displaystyle{ \Eta(Y|X) \,=\, \Eta(X|Y) - \Eta(X) + \Eta(Y). }[/math]
Proof. [math]\displaystyle{ \Eta(Y|X) = \Eta(X,Y) - \Eta(X) }[/math] and [math]\displaystyle{ \Eta(X|Y) = \Eta(Y,X) - \Eta(Y) }[/math]. Symmetry entails [math]\displaystyle{ \Eta(X,Y) = \Eta(Y,X) }[/math]. Subtracting the two equations implies Bayes' rule.
If [math]\displaystyle{ Y }[/math] is conditionally independent of [math]\displaystyle{ Z }[/math] given [math]\displaystyle{ X }[/math] we have:
- [math]\displaystyle{ \Eta(Y|X,Z) \,=\, \Eta(Y|X). }[/math]
Other properties
For any [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math]:
- [math]\displaystyle{ \begin{align} \Eta(Y|X) &\le \Eta(Y) \, \\ \Eta(X,Y) &= \Eta(X|Y) + \Eta(Y|X) + \operatorname{I}(X;Y),\qquad \\ \Eta(X,Y) &= \Eta(X) + \Eta(Y) - \operatorname{I}(X;Y),\, \\ \operatorname{I}(X;Y) &\le \Eta(X),\, \end{align} }[/math]
where [math]\displaystyle{ \operatorname{I}(X;Y) }[/math] is the mutual information between [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math].
For independent [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math]:
- [math]\displaystyle{ \Eta(Y|X) = \Eta(Y) }[/math] and [math]\displaystyle{ \Eta(X|Y) = \Eta(X) \, }[/math]
Although the specific-conditional entropy [math]\displaystyle{ \Eta(X|Y=y) }[/math] can be either less or greater than [math]\displaystyle{ \Eta(X) }[/math] for a given random variate [math]\displaystyle{ y }[/math] of [math]\displaystyle{ Y }[/math], [math]\displaystyle{ \Eta(X|Y) }[/math] can never exceed [math]\displaystyle{ \Eta(X) }[/math].
Conditional differential entropy
Definition
The above definition is for discrete random variables. The continuous version of discrete conditional entropy is called conditional differential (or continuous) entropy. Let [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] be a continuous random variables with a joint probability density function [math]\displaystyle{ f(x,y) }[/math]. The differential conditional entropy [math]\displaystyle{ h(X|Y) }[/math] is defined as[3]:249
[math]\displaystyle{ h(X|Y) = -\int_{\mathcal X, \mathcal Y} f(x,y)\log f(x|y)\,dx dy }[/math]
|
|
(Eq.2) |
Properties
In contrast to the conditional entropy for discrete random variables, the conditional differential entropy may be negative.
As in the discrete case there is a chain rule for differential entropy:
- [math]\displaystyle{ h(Y|X)\,=\,h(X,Y)-h(X) }[/math][3]:253
Notice however that this rule may not be true if the involved differential entropies do not exist or are infinite.
Joint differential entropy is also used in the definition of the mutual information between continuous random variables:
- [math]\displaystyle{ \operatorname{I}(X,Y)=h(X)-h(X|Y)=h(Y)-h(Y|X) }[/math]
[math]\displaystyle{ h(X|Y) \le h(X) }[/math] with equality if and only if [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] are independent.[3]:253
Relation to estimator error
The conditional differential entropy yields a lower bound on the expected squared error of an estimator. For any random variable [math]\displaystyle{ X }[/math], observation [math]\displaystyle{ Y }[/math] and estimator [math]\displaystyle{ \widehat{X} }[/math] the following holds:[3]:255
- [math]\displaystyle{ \mathbb{E}\left[\bigl(X - \widehat{X}{(Y)}\bigr)^2\right] \ge \frac{1}{2\pi e}e^{2h(X|Y)} }[/math]
This is related to the uncertainty principle from quantum mechanics.
Generalization to quantum theory
In quantum information theory, the conditional entropy is generalized to the conditional quantum entropy. The latter can take negative values, unlike its classical counterpart.
See also
- Entropy (information theory)
- Mutual information
- Conditional quantum entropy
- Variation of information
- Entropy power inequality
- Likelihood function
References
- ↑ "David MacKay: Information Theory, Pattern Recognition and Neural Networks: The Book". www.inference.org.uk. Retrieved 2019-10-25.
- ↑ Hellman, M.; Raviv, J. (1970). "Probability of error, equivocation, and the Chernoff bound". IEEE Transactions on Information Theory. 16 (4): 368–372.
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 3.6 T. Cover; J. Thomas (1991). Elements of Information Theory. ISBN 0-471-06259-6. https://archive.org/details/elementsofinform0000cove.