“奇点”的版本间的差异

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
跳到导航 跳到搜索
第1行： 第1行：
−
此词条暂由彩云小译翻译，翻译字数共606，未经人工整理和审校，带来阅读不便，请见谅。
+
此词条暂由彩云小译翻译，翻译字数共1231，未经人工整理和审校，带来阅读不便，请见谅。
  
 
{{short description|Point where a function, a curve or another mathematical object does not behave regularly}}
 
{{short description|Point where a function, a curve or another mathematical object does not behave regularly}}
第13行： 第13行：
 
For example, the [[function of a real variable|real function]]
 
For example, the [[function of a real variable|real function]]
  
 +
For example, the real function
  
 +
例如，真正的函数
  
−
Other than isolated singularities, complex functions of one variable may exhibit other singular behaviour. These are termed nonisolated singularities, of which there are two types:
 
  
−
除孤立奇点外，一个变量的复变函数还可能表现出其他奇异行为。这些称为非孤立奇点，其中有两种类型:
 
  
 
:<math> f(x)=\frac{1}{x} </math>
 
:<math> f(x)=\frac{1}{x} </math>
 +
 +
<math> f(x)=\frac{1}{x} </math>
 +
 +
= frac {1}{ x } </math >
  
  
  
 
has a singularity at <math>x = 0</math>, where it seems to "explode" to <math>\pm\infty</math> and is hence not defined. The [[absolute value]] function <math>g(x) = |x|</math> also has a singularity at {{math|1=''x'' = 0}}, since it is not [[Differentiable function|differentiable]] there.<ref name=":0" /><ref>{{cite book |first=Geoffrey C. |last=Berresford |first2=Andrew M. |last2=Rockett |title=Applied Calculus |location= |publisher=Cengage Learning |year=2015 |isbn= 978-1-305-46505-3|page=151 |url=https://books.google.com/books?id=wzNBBAAAQBAJ&pg=PA151 }}</ref>
 
has a singularity at <math>x = 0</math>, where it seems to "explode" to <math>\pm\infty</math> and is hence not defined. The [[absolute value]] function <math>g(x) = |x|</math> also has a singularity at {{math|1=''x'' = 0}}, since it is not [[Differentiable function|differentiable]] there.<ref name=":0" /><ref>{{cite book |first=Geoffrey C. |last=Berresford |first2=Andrew M. |last2=Rockett |title=Applied Calculus |location= |publisher=Cengage Learning |year=2015 |isbn= 978-1-305-46505-3|page=151 |url=https://books.google.com/books?id=wzNBBAAAQBAJ&pg=PA151 }}</ref>
 +
 +
has a singularity at <math>x = 0</math>, where it seems to "explode" to <math>\pm\infty</math> and is hence not defined. The absolute value function <math>g(x) = |x|</math> also has a singularity at , since it is not differentiable there.
 +
 +
有一个奇点在 < math > x = 0 </math > ，它似乎“爆炸”到 < math > pm infty </math > ，因此没有定义。绝对值函数 < math > g (x) = | x | </math > 也有一个奇点，因为它在那里是不可微的。
  
  
第29行： 第37行：
 
The [[algebraic curve]] defined by <math>\{(x,y):y^3-x^2=0\}</math> in the <math>(x, y)</math> coordinate system has a singularity (called a [[cusp (singularity)|cusp]]) at <math>(0, 0)</math>. For singularities in [[algebraic geometry]], see [[singular point of an algebraic variety]]. For singularities in [[differential geometry]], see [[singularity theory]].
 
The [[algebraic curve]] defined by <math>\{(x,y):y^3-x^2=0\}</math> in the <math>(x, y)</math> coordinate system has a singularity (called a [[cusp (singularity)|cusp]]) at <math>(0, 0)</math>. For singularities in [[algebraic geometry]], see [[singular point of an algebraic variety]]. For singularities in [[differential geometry]], see [[singularity theory]].
  
 +
The algebraic curve defined by <math>\{(x,y):y^3-x^2=0\}</math> in the <math>(x, y)</math> coordinate system has a singularity (called a cusp) at <math>(0, 0)</math>. For singularities in algebraic geometry, see singular point of an algebraic variety. For singularities in differential geometry, see singularity theory.
  
 +
代数曲线定义于 math > (x，y) : y ^ 3-x ^ 2 = 0} </math > (x，y) </math > 坐标系在 math > (0,0) </math > 上有一个奇点(叫做尖点)。关于代数几何的奇点，请参阅《非奇异。关于微分几何的奇点，请参阅《奇点理论。
  
−
Branch points are generally the result of a multi-valued function, such as <math>\sqrt{z}</math> or <math>\log(z)</math>, which are defined within a certain limited domain so that the function can be made single-valued within the domain. The cut is a line or curve excluded from the domain to introduce a technical separation between discontinuous values of the function. When the cut is genuinely required, the function will have distinctly different values on each side of the branch cut. The shape of the branch cut is a matter of choice, even though it must connect two different branch points (such as <math>z=0</math> and <math>z=\infty</math> for <math>\log(z)</math>) which are fixed in place.
 
  
−
分支点通常是多值函数的结果，比如 < math > sqrt { z } </math > 或 < math > log (z) </math > ，这些分支点定义在一个特定的有限域内，因此函数可以在域内成为单值函数。切割是一条从区域中排除的直线或曲线，它在函数的不连续值之间引入了一种技术上的分离。当切割是真正需要的，功能将有明显不同的价值观在每一侧的分支削减。分支切口的形状是一个选择的问题，即使它必须连接两个不同的分支点(如 < math > z = 0 </math > 和 < math > z = infty </math > for < math > log (z) </math >) ，这两个分支点是固定的。
 
  
 
==Real analysis==
 
==Real analysis==
第39行： 第47行：
 
In [[real analysis]], singularities are either [[classification of discontinuities|discontinuities]], or discontinuities of the [[derivative]] (sometimes also discontinuities of higher order derivatives). There are four kinds of discontinuities: '''type&nbsp;I''', which has two subtypes, and '''type&nbsp;II''', which can also be divided into two subtypes (though usually is not).
 
In [[real analysis]], singularities are either [[classification of discontinuities|discontinuities]], or discontinuities of the [[derivative]] (sometimes also discontinuities of higher order derivatives). There are four kinds of discontinuities: '''type&nbsp;I''', which has two subtypes, and '''type&nbsp;II''', which can also be divided into two subtypes (though usually is not).
  
 +
In real analysis, singularities are either discontinuities, or discontinuities of the derivative (sometimes also discontinuities of higher order derivatives). There are four kinds of discontinuities: type&nbsp;I, which has two subtypes, and type&nbsp;II, which can also be divided into two subtypes (though usually is not).
  
 +
在实际分析中，奇点要么是导数的不连续性，要么是导数的不连续性(有时也是高阶导数的不连续性)。有四种不连续性: i 型(有两个子类型)和 II 型(也可以分为两个子类型(虽然通常不是)。
  
−
The [[reciprocal function, exhibiting hyperbolic growth.]]<!-- A better image would be 1/(1-x) or similar, showing a positive singular point and growth as x increases -->
 
  
−
[[倒数函数，显示双曲增长。[] < ! -- 一个更好的图像应该是1/(1-x)或类似的图像，显示一个正的奇点，并且随着 x 的增加而增长 -- >
 
  
 
To describe the way these two types of limits are being used, suppose that <math>f(x)</math> is a function of a real argument <math>x</math>, and for any value of its argument, say <math>c</math>, then the '''left-handed limit''', <math>f(c^-)</math>, and the '''right-handed limit''', <math>f(c^+)</math>, are defined by:
 
To describe the way these two types of limits are being used, suppose that <math>f(x)</math> is a function of a real argument <math>x</math>, and for any value of its argument, say <math>c</math>, then the '''left-handed limit''', <math>f(c^-)</math>, and the '''right-handed limit''', <math>f(c^+)</math>, are defined by:
 +
 +
To describe the way these two types of limits are being used, suppose that <math>f(x)</math> is a function of a real argument <math>x</math>, and for any value of its argument, say <math>c</math>, then the left-handed limit, <math>f(c^-)</math>, and the right-handed limit, <math>f(c^+)</math>, are defined by:
 +
 +
为了描述这两种类型的限制被使用的方式，假设 < math > f (x) </math > 是一个实参数的函数 < math > x </math > ，并且对于它的参数的任何值，比如 < math > c </math > ，那么左手限制 < math > f (c ^ -) </math > ，和右手限制 < math > f (c ^ +) </math，定义为:
  
 
:<math>f(c^-) = \lim_{x \to c}f(x)</math>, constrained by <math>x < c</math> and
 
:<math>f(c^-) = \lim_{x \to c}f(x)</math>, constrained by <math>x < c</math> and
  
−
A finite-time singularity occurs when one input variable is time, and an output variable increases towards infinity at a finite time. These are important in kinematics and PDEs (Partial Differential Equations) – infinites do not occur physically, but the behavior near the singularity is often of interest. Mathematically, the simplest finite-time singularities are power laws for various exponents of the form <math>x^{-\alpha},</math> of which the simplest is hyperbolic growth, where the exponent is (negative) 1: <math>x^{-1}.</math> More precisely, in order to get a singularity at positive time as time advances (so the output grows to infinity), one instead uses <math>(t_0-t)^{-\alpha}</math> (using t for time, reversing direction to <math>-t</math> so that time increases to infinity, and shifting the singularity forward from 0 to a fixed time <math>t_0</math>).
+
<math>f(c^-) = \lim_{x \to c}f(x)</math>, constrained by <math>x < c</math> and
  
−
当一个输入变量为时间，输出变量在有限时间内向无穷大方向增长时，出现了有限时间奇异性。这些在运动学和偏微分方程(偏微分方程)中很重要——物理上不存在无穷大，但奇点附近的行为通常是有趣的。数学上，最简单的有限时间奇点是形式为 < math > x ^ {-alpha }的各种指数的幂律，其中最简单的是双曲增长，其指数是(负)1: < math > x ^ {-1}。更准确地说，为了在正时间得到一个奇点，随着时间的推移(所以输出增长到无穷大) ，取而代之的是使用 < math > (t _ 0-t) ^ {-alpha } </math > (使用 t 表示时间，将方向倒转到 < math >-t </math > ，使时间增长到无穷大，并将奇点从0向前移动到一个固定的时间 < t _ 0 </math >)。
+
[ math > f (c ^ -) = lim _ { x to c } f (x) </math > ，受到 < math > x </math > 和 </math > 的约束
  
  
第57行： 第69行：
 
:<math>f(c^+) = \lim_{x \to c}f(x)</math>, constrained by <math>x > c</math>.
 
:<math>f(c^+) = \lim_{x \to c}f(x)</math>, constrained by <math>x > c</math>.
  
−
An example would be the bouncing motion of an inelastic ball on a plane. If idealized motion is considered, in which the same fraction of kinetic energy is lost on each bounce, the frequency of bounces becomes infinite, as the ball comes to rest in a finite time. Other examples of finite-time singularities include the various forms of the Painlevé paradox (for example, the tendency of a chalk to skip when dragged across a blackboard), and how the precession rate of a coin spun on a flat surface accelerates towards infinite—before abruptly stopping (as studied using the Euler's Disk toy).
+
<math>f(c^+) = \lim_{x \to c}f(x)</math>, constrained by <math>x > c</math>.
  
−
一个例子是一个非弹性球在平面上的反弹运动。如果考虑理想运动，即每次弹跳都损失相同的动能，那么弹跳的频率就是无限的，因为球停在一个有限的时间里。有限时间奇点的其他例子包括 painlevé 悖论的各种形式(例如，当粉笔被拖过黑板时，粉笔倾向于跳过) ，以及在平面上旋转的硬币的进动速率如何加速到无限ー然后突然停止(使用欧拉圆盘玩具进行的研究)。
+
[ math > f (c ^ +) = lim _ { x to c } f (x) </math > ，受 < math > x > c </math > 约束。
  
  
第65行： 第77行：
 
The value <math>f(c^-)</math> is the value that the function <math>f(x)</math> tends towards as the value <math>x</math> approaches <math>c</math> from ''below'', and the value <math>f(c^+)</math> is the value that the function <math>f(x)</math> tends towards as the value <math>x</math> approaches <math>c</math> from ''above'', regardless of the actual value the function has at the point where <math>x = c</math>&nbsp;.
 
The value <math>f(c^-)</math> is the value that the function <math>f(x)</math> tends towards as the value <math>x</math> approaches <math>c</math> from ''below'', and the value <math>f(c^+)</math> is the value that the function <math>f(x)</math> tends towards as the value <math>x</math> approaches <math>c</math> from ''above'', regardless of the actual value the function has at the point where <math>x = c</math>&nbsp;.
  
−
Hypothetical examples include Heinz von Foerster's facetious "Doomsday's equation" (simplistic models yield infinite human population in finite time).
+
The value <math>f(c^-)</math> is the value that the function <math>f(x)</math> tends towards as the value <math>x</math> approaches <math>c</math> from below, and the value <math>f(c^+)</math> is the value that the function <math>f(x)</math> tends towards as the value <math>x</math> approaches <math>c</math> from above, regardless of the actual value the function has at the point where <math>x = c</math>&nbsp;.
 +
 
 +
值 < math > f (c ^ -) </math > 是函数 < math > f (x) </math > 趋向于下面的值 < math > x </math > 接近 < math > c </math > ，值 < math > f (c ^ +) </math > 是函数 < math > f (x) </math > 趋向于上面的值 < math > x </math > 接近 math > c </math > ，而不管函数在数学上的实际值 < x = c </math > 。
  
−
假设的例子包括 Heinz von Foerster 滑稽的“末日方程”(简单化的模型在有限的时间里产生无限的人口)。
 
  
  
 +
There are some functions for which these limits do not exist at all. For example, the function
  
 
There are some functions for which these limits do not exist at all. For example, the function
 
There are some functions for which these limits do not exist at all. For example, the function
 +
 +
有些函数根本不存在这些限制。例如，函数
  
 
:<math>g(x) = \sin\left(\frac{1}{x}\right)</math>
 
:<math>g(x) = \sin\left(\frac{1}{x}\right)</math>
  
−
In algebraic geometry, a singularity of an algebraic variety is a point of the variety where the tangent space may not be regularly defined. The simplest example of singularities are curves that cross themselves. But there are other types of singularities, like cusps. For example, the equation  − x = 0 }} defines a curve that has a cusp at the origin . One could define the -axis as a tangent at this point, but this definition can not be the same as the definition at other points. In fact, in this case, the -axis is a "double tangent."
+
<math>g(x) = \sin\left(\frac{1}{x}\right)</math>
  
−
在代数几何中，代数簇的奇点是各种各样的切线空间可能没有规则定义的一点。奇点最简单的例子就是它们自己交叉的曲线。但是还有其他类型的奇点，比如尖点。例如，方程 -x = 0}}定义了一条在原点有尖点的曲线。可以将-轴定义为这一点的切线，但这个定义不能与其他点的定义相同。实际上，在这种情况下,-轴是一个“双切线”
+
< math > g (x) = sin left (frac {1}{ x } right) </math >
  
 
does not tend towards anything as <math>x</math> approaches <math>c = 0</math>. The limits in this case are not infinite, but rather [[Undefined (mathematics)|undefined]]: there is no value that <math>g(x)</math> settles in on. Borrowing from complex analysis, this is sometimes called an ''[[essential singularity]]''.
 
does not tend towards anything as <math>x</math> approaches <math>c = 0</math>. The limits in this case are not infinite, but rather [[Undefined (mathematics)|undefined]]: there is no value that <math>g(x)</math> settles in on. Borrowing from complex analysis, this is sometimes called an ''[[essential singularity]]''.
  
 +
does not tend towards anything as <math>x</math> approaches <math>c = 0</math>. The limits in this case are not infinite, but rather undefined: there is no value that <math>g(x)</math> settles in on. Borrowing from complex analysis, this is sometimes called an essential singularity.
  
 +
不倾向于做任何事情，因为。在这种情况下，限制不是无限的，而是未定义的: 没有一个值是 < math > g (x) </math > 的。借用复杂的分析，这有时被称为本质奇点。
  
−
For affine and projective varieties, the singularities are the points where the Jacobian matrix has a rank which is lower than at other points of the variety.
 
  
−
对于仿射变种和射影变种，奇异点是指雅可比矩阵的秩低于其它变种点的点。
 
  
 
The possible cases at a given value <math>c</math> for the argument are as follows.
 
The possible cases at a given value <math>c</math> for the argument are as follows.
  
−
* A '''point of continuity''' is a value of <math>c</math> for which <math>f(c^-) = f(c) = f(c^+)</math>, as one expects for a smooth function. All the values must be finite. If <math>c</math> is not a point of continuity, then a discontinuity occurs at <math>c</math>.
+
The possible cases at a given value <math>c</math> for the argument are as follows.
  
−
An equivalent definition in terms of commutative algebra may be given, which extends to abstract varieties and schemes: A point is singular if the local ring at this point is not a regular local ring.
+
参数在给定值 < math > c </math > 下的可能情况如下。
  
−
可以给出一个关于交换代数的等价定义，它扩展到抽象的簇和方案: 如果局部环在这一点上不是一个正则局部环，那么一个点就是奇异的。
+
* A '''point of continuity''' is a value of <math>c</math> for which <math>f(c^-) = f(c) = f(c^+)</math>, as one expects for a smooth function. All the values must be finite. If <math>c</math> is not a point of continuity, then a discontinuity occurs at <math>c</math>.
  
 
* A '''type&nbsp;I''' discontinuity occurs when both <math>f(c^-)</math> and <math>f(c^+)</math> exist and are finite, but at least one of the following three conditions also applies:
 
* A '''type&nbsp;I''' discontinuity occurs when both <math>f(c^-)</math> and <math>f(c^+)</math> exist and are finite, but at least one of the following three conditions also applies:
第104行： 第120行：
  
 
:Type I discontinuities can be further distinguished as being one of the following subtypes:
 
:Type I discontinuities can be further distinguished as being one of the following subtypes:
 +
 +
Type I discontinuities can be further distinguished as being one of the following subtypes:
 +
 +
第一类不连续性可以进一步区分为下列子类型之一:
  
 
:* A '''[[jump discontinuity]]''' occurs when <math>f(c^-) \neq f(c^+)</math>, regardless of whether <math>f(c)</math> is defined, and regardless of its value if it is defined.
 
:* A '''[[jump discontinuity]]''' occurs when <math>f(c^-) \neq f(c^+)</math>, regardless of whether <math>f(c)</math> is defined, and regardless of its value if it is defined.
 +
 +
* A jump discontinuity occurs when <math>f(c^-) \neq f(c^+)</math>, regardless of whether <math>f(c)</math> is defined, and regardless of its value if it is defined.
 +
 +
* 当 < math > f (c ^ -) neq f (c ^ +) </math > ，不管 < math > f (c) </math > 是否定义，也不管是否定义了它的值时，就会发生跳转不连续性。
  
 
:* A '''[[removable singularity|removable discontinuity]]''' occurs when <math>f(c^-) = f(c^+)</math>, also regardless of whether <math>f(c)</math> is defined, and regardless of its value if it is defined (but which does not match that of the two limits).
 
:* A '''[[removable singularity|removable discontinuity]]''' occurs when <math>f(c^-) = f(c^+)</math>, also regardless of whether <math>f(c)</math> is defined, and regardless of its value if it is defined (but which does not match that of the two limits).
 +
 +
* A removable discontinuity occurs when <math>f(c^-) = f(c^+)</math>, also regardless of whether <math>f(c)</math> is defined, and regardless of its value if it is defined (but which does not match that of the two limits).
 +
 +
* 当 < math > f (c ^ -) = f (c ^ +) </math > ，也不管 < math > f (c) </math > 是否已定义，也不管是否已定义它的值(但不匹配两个极限)时，就会出现可移动的不连续性。
  
 
* A '''type&nbsp;II''' discontinuity occurs when either <math>f(c^-)</math> or <math>f(c^+)</math> does not exist (possibly both). This has two subtypes, which are usually not considered separately:
 
* A '''type&nbsp;II''' discontinuity occurs when either <math>f(c^-)</math> or <math>f(c^+)</math> does not exist (possibly both). This has two subtypes, which are usually not considered separately:
第118行： 第146行：
  
 
In real analysis, a singularity or discontinuity is a property of a function alone. Any singularities that may exist in the derivative of a function are considered as belonging to the derivative, not to the original function.
 
In real analysis, a singularity or discontinuity is a property of a function alone. Any singularities that may exist in the derivative of a function are considered as belonging to the derivative, not to the original function.
 +
 +
In real analysis, a singularity or discontinuity is a property of a function alone. Any singularities that may exist in the derivative of a function are considered as belonging to the derivative, not to the original function.
 +
 +
在实际分析中，奇点或不连续是函数本身的一个性质。任何可能存在于函数导数中的奇点都被认为是属于导数，而不是原函数。
  
  
第126行： 第158行：
  
 
A '''coordinate singularity''' occurs when an apparent singularity or discontinuity occurs in one coordinate frame, which can be removed by choosing a different frame. An example of this is the apparent singularity at the 90 degree latitude in [[spherical coordinates]]. An object moving due north (for example, along the line 0 degrees longitude) on the surface of a sphere will suddenly experience an instantaneous change in longitude at the pole (in the case of the example, jumping from longitude 0 to longitude 180 degrees).  This discontinuity, however, is only apparent; it is an artifact of the coordinate system chosen, which is singular at the poles.  A different coordinate system would eliminate the apparent discontinuity (e.g., by replacing the latitude/longitude representation with an [[n-vector|{{mvar|n}}-vector]] representation).
 
A '''coordinate singularity''' occurs when an apparent singularity or discontinuity occurs in one coordinate frame, which can be removed by choosing a different frame. An example of this is the apparent singularity at the 90 degree latitude in [[spherical coordinates]]. An object moving due north (for example, along the line 0 degrees longitude) on the surface of a sphere will suddenly experience an instantaneous change in longitude at the pole (in the case of the example, jumping from longitude 0 to longitude 180 degrees).  This discontinuity, however, is only apparent; it is an artifact of the coordinate system chosen, which is singular at the poles.  A different coordinate system would eliminate the apparent discontinuity (e.g., by replacing the latitude/longitude representation with an [[n-vector|{{mvar|n}}-vector]] representation).
 +
 +
A coordinate singularity occurs when an apparent singularity or discontinuity occurs in one coordinate frame, which can be removed by choosing a different frame. An example of this is the apparent singularity at the 90 degree latitude in spherical coordinates. An object moving due north (for example, along the line 0 degrees longitude) on the surface of a sphere will suddenly experience an instantaneous change in longitude at the pole (in the case of the example, jumping from longitude 0 to longitude 180 degrees).  This discontinuity, however, is only apparent; it is an artifact of the coordinate system chosen, which is singular at the poles.  A different coordinate system would eliminate the apparent discontinuity (e.g., by replacing the latitude/longitude representation with an -vector representation).
 +
 +
当在一个坐标系中出现明显的奇异或不连续时，就会出现坐标奇异性，这可以通过选择不同的坐标系来消除。这方面的一个例子是球坐标系中90度纬度处的明显奇点。在球体表面向北移动的物体(例如，沿着0度经线)在极点会突然经历经度的瞬时变化(例如，从0度经度跳到180度经度)。然而，这种不连续性只是显而易见的，它是所选择的坐标系的人工制品，在极点是奇异的。不同的坐标系将消除明显的不连续性(例如，将纬度/经度表示替换为-vector 表示)。
 +
 +
 +
 +
==Complex analysis==
 +
 +
In [[complex analysis]], there are several classes of singularities. These include the isolated singularities, the nonisolated singularities and the branch points.
 +
 +
In complex analysis, there are several classes of singularities. These include the isolated singularities, the nonisolated singularities and the branch points.
 +
 +
在复分析中，有几类奇异点。其中包括孤立奇点、非孤立奇点和分支点。
 +
 +
 +
 +
===Isolated singularities===
 +
 +
Suppose that ''U'' is an [[open set|open subset]] of the [[complex number]]s '''C''', with the point ''a'' being an element of ''U'', and that ''f'' is a [[holomorphic function|complex differentiable function]] defined on some [[Neighbourhood (mathematics)|neighborhood]] around ''a'', excluding ''a'': ''U'' \ {''a''}, then:
 +
 +
Suppose that U is an open subset of the complex numbers C, with the point a being an element of U, and that f is a complex differentiable function defined on some neighborhood around a, excluding a: U \ {a}, then:
 +
 +
假设 u 是复数 c 的一个开子集，点 a 是 u 的一个元素，而 f 是定义在 a 周围某个邻域上的复可微函数，除了 a: u { a } ，那么:
 +
 +
* The point ''a'' is a [[removable singularity]] of ''f'' if there exists a [[holomorphic function]] ''g'' defined on all of ''U'' such that ''f''(''z'') = ''g''(''z'') for all ''z'' in ''U'' \ {''a''}. The function ''g'' is a continuous replacement for the function ''f''.<ref>{{Cite web|url=http://mathworld.wolfram.com/Singularity.html|title=Singularity|last=Weisstein|first=Eric W.|website=mathworld.wolfram.com|language=en|access-date=2019-12-12}}</ref>
 +
 +
* The point ''a'' is a [[pole (complex analysis)|pole]] or non-essential singularity of ''f''  if there exists a holomorphic function ''g'' defined on ''U'' with ''g''(''a'') nonzero, and a [[natural number]] ''n'' such that ''f''(''z'') = ''g''(''z'') / (''z'' − ''a'')<sup>''n''</sup> for all ''z'' in ''U'' \ {''a''}. The least such number ''n'' is called the ''order of the pole''. The derivative at a non-essential singularity itself has a non-essential singularity, with ''n'' increased by 1 (except if ''n'' is 0 so that the singularity is removable).
 +
 +
* The point ''a'' is an [[essential singularity]] of ''f'' if it is neither a removable singularity nor a pole. The point ''a'' is an essential singularity [[iff|if and only if]] the [[Laurent series]] has infinitely many powers of negative degree.<ref name=":1" />
 +
 +
 +
 +
===Nonisolated singularities===
 +
 +
Other than isolated singularities, complex functions of one variable may exhibit other singular behaviour. These are termed nonisolated singularities, of which there are two types:
 +
 +
Other than isolated singularities, complex functions of one variable may exhibit other singular behaviour. These are termed nonisolated singularities, of which there are two types:
 +
 +
除孤立奇点外，一个变量的复变函数还可能表现出其他奇异行为。这些称为非孤立奇点，其中有两种类型:
 +
 +
 +
 +
* '''Cluster points''': [[limit points]] of isolated singularities. If they are all poles, despite admitting [[Laurent series]] expansions on each of them, then no such expansion is possible at its limit.
 +
 +
* '''Natural boundaries''': any non-isolated set (e.g. a curve) on which functions cannot be [[analytic continuation|analytically continued]] around (or outside them if they are closed curves in the [[Riemann sphere]]).
 +
 +
 +
 +
===Branch points===
 +
 +
[[Branch point]]s are generally the result of a [[multi-valued function]], such as <math>\sqrt{z}</math> or <math>\log(z)</math>, which are defined within a certain limited domain so that the function can be made single-valued within the domain. The cut is a line or curve excluded from the domain to introduce a technical separation between discontinuous values of the function. When the cut is genuinely required, the function will have distinctly different values on each side of the branch cut. The shape of the branch cut is a matter of choice, even though it must connect two different branch points (such as <math>z=0</math> and <math>z=\infty</math> for <math>\log(z)</math>) which are fixed in place.
 +
 +
Branch points are generally the result of a multi-valued function, such as <math>\sqrt{z}</math> or <math>\log(z)</math>, which are defined within a certain limited domain so that the function can be made single-valued within the domain. The cut is a line or curve excluded from the domain to introduce a technical separation between discontinuous values of the function. When the cut is genuinely required, the function will have distinctly different values on each side of the branch cut. The shape of the branch cut is a matter of choice, even though it must connect two different branch points (such as <math>z=0</math> and <math>z=\infty</math> for <math>\log(z)</math>) which are fixed in place.
 +
 +
分支点通常是多值函数的结果，比如 < math > sqrt { z } </math > 或 < math > log (z) </math > ，这些分支点定义在一个特定的有限域内，因此函数可以在域内成为单值函数。切割是一条从区域中排除的直线或曲线，用以在不连续的函数值之间进行技术上的分离。当切割是真正需要的，功能将有明显不同的价值观在每一侧的分支削减。分支切口的形状是一个选择问题，即使它必须连接两个不同的分支点(比如 < math > z = 0 </math > 和 < math > z = infty </math > ，用于 < math > log (z) </math >) ，这两个分支点是固定的。
 +
 +
 +
 +
==Finite-time singularity==
 +
 +
[[File:Rectangular hyperbola.svg|thumb|The [[reciprocal function]], exhibiting [[hyperbolic growth]].]]<!-- A better image would be 1/(1-x) or similar, showing a positive singular point and growth as x increases -->
 +
 +
The [[reciprocal function, exhibiting hyperbolic growth.]]<!-- A better image would be 1/(1-x) or similar, showing a positive singular point and growth as x increases -->
 +
 +
[[倒数函数，显示双曲增长。[] < ! -- 一个更好的图像应该是1/(1-x)或类似的图像，显示一个正的奇点，并且随着 x 的增加而增长 -- >
 +
 +
 +
 +
A '''finite-time singularity''' occurs when one input variable is time, and an output variable increases towards infinity at a finite time. These are important in [[kinematic]]s and PDEs ([[Partial differential equation|Partial Differential Equations]]) – infinites do not occur physically, but the behavior near the singularity is often of interest. Mathematically, the simplest finite-time singularities are [[power law]]s for various exponents of the form <math>x^{-\alpha},</math> of which the simplest is [[hyperbolic growth]], where the exponent is (negative) 1: <math>x^{-1}.</math> More precisely, in order to get a singularity at positive time as time advances (so the output grows to infinity), one instead uses <math>(t_0-t)^{-\alpha}</math> (using ''t'' for time, reversing direction to <math>-t</math> so that time increases to infinity, and shifting the singularity forward from 0 to a fixed time <math>t_0</math>).
 +
 +
A finite-time singularity occurs when one input variable is time, and an output variable increases towards infinity at a finite time. These are important in kinematics and PDEs (Partial Differential Equations) – infinites do not occur physically, but the behavior near the singularity is often of interest. Mathematically, the simplest finite-time singularities are power laws for various exponents of the form <math>x^{-\alpha},</math> of which the simplest is hyperbolic growth, where the exponent is (negative) 1: <math>x^{-1}.</math> More precisely, in order to get a singularity at positive time as time advances (so the output grows to infinity), one instead uses <math>(t_0-t)^{-\alpha}</math> (using t for time, reversing direction to <math>-t</math> so that time increases to infinity, and shifting the singularity forward from 0 to a fixed time <math>t_0</math>).
 +
 +
当输入变量为时间，输出变量在有限时间内向无穷大方向增长时，出现有限时间奇异性。这些在运动学和偏微分方程(偏微分方程)中都很重要——物理上不存在无穷大，但奇点附近的行为通常是有趣的。数学上，最简单的有限时间奇点是形式为 < math > x ^ {-alpha }的各种指数的幂律，其中最简单的是双曲增长，其指数是(负)1: < math > x ^ {-1}。更准确地说，为了在正时间得到一个奇点，随着时间的推移(所以输出增加到无穷大) ，一个代替使用 < math > (t _ 0-t) ^ {-alpha } </math > (使用 t 表示时间，倒转方向到 < math >-t </math > ，所以时间增加到无穷大，并将奇点从0向前移动到一个固定的时间 < t _ 0 </math >)。
 +
 +
 +
 +
An example would be the bouncing motion of an inelastic ball on a plane. If idealized motion is considered, in which the same fraction of [[kinetic energy]] is lost on each bounce, the [[frequency]] of bounces becomes infinite, as the ball comes to rest in a finite time. Other examples of finite-time singularities include the various forms of the [[Painlevé paradox]] (for example, the tendency of a chalk to skip when dragged across a blackboard), and how the [[precession]] rate of a [[coin]] spun on a flat surface accelerates towards infinite—before abruptly stopping (as studied using the [[Euler's Disk]] toy).
 +
 +
An example would be the bouncing motion of an inelastic ball on a plane. If idealized motion is considered, in which the same fraction of kinetic energy is lost on each bounce, the frequency of bounces becomes infinite, as the ball comes to rest in a finite time. Other examples of finite-time singularities include the various forms of the Painlevé paradox (for example, the tendency of a chalk to skip when dragged across a blackboard), and how the precession rate of a coin spun on a flat surface accelerates towards infinite—before abruptly stopping (as studied using the Euler's Disk toy).
 +
 +
一个例子是一个非弹性球在平面上的反弹运动。如果考虑理想运动，即每次弹跳都损失相同的动能，那么弹跳的频率就是无限的，因为球停在一个有限的时间里。有限时间奇点的其他例子包括各种形式的 painlevé 悖论(例如，粉笔在黑板上拖动时会跳过) ，以及在平面上旋转的硬币的进动速率如何加速到无限，然后突然停止(用欧拉圆盘玩具进行的研究)。
 +
 +
 +
 +
Hypothetical examples include [[Heinz von Foerster]]'s facetious "[[Heinz von Foerster#Doomsday equation|Doomsday's equation]]" (simplistic models yield infinite human population in finite time).
 +
 +
Hypothetical examples include Heinz von Foerster's facetious "Doomsday's equation" (simplistic models yield infinite human population in finite time).
 +
 +
假设的例子包括 Heinz von Foerster 滑稽的“末日方程”(简单化的模型在有限的时间里产生无限的人口)。
 +
 +
 +
 +
==Algebraic geometry and commutative algebra==
 +
 +
In [[algebraic geometry]], a [[singular point of an algebraic variety|singularity of an algebraic variety]] is a point of the variety where the [[tangent space]] may not be regularly defined. The simplest example of singularities are curves that cross themselves. But there are other types of singularities, like [[cusp (singularity)|cusps]]. For example, the equation {{math|1= ''y''{{sup|2}} − ''x''{{sup|3}} = 0 }} defines a curve that has a cusp at the origin {{math|1= ''x'' = ''y'' = 0 }}. One could define the {{math|''x''}}-axis as a tangent at this point, but this definition can not be the same as the definition at other points. In fact, in this case, the {{math|''x''}}-axis is a "double tangent."
 +
 +
In algebraic geometry, a singularity of an algebraic variety is a point of the variety where the tangent space may not be regularly defined. The simplest example of singularities are curves that cross themselves. But there are other types of singularities, like cusps. For example, the equation  − x = 0 }} defines a curve that has a cusp at the origin . One could define the -axis as a tangent at this point, but this definition can not be the same as the definition at other points. In fact, in this case, the -axis is a "double tangent."
 +
 +
在代数几何中，代数簇的奇点是各种各样的切线空间可能没有规则定义的一点。奇点最简单的例子就是它们自己交叉的曲线。但是还有其他类型的奇点，比如尖点。例如，方程 -x = 0}}定义了一条在原点有尖点的曲线。可以将-轴定义为这一点的切线，但这个定义不能与其他点的定义相同。实际上，在这种情况下,-轴是一个“双切线”
 +
 +
 +
 +
For [[affine variety|affine]] and [[projective variety|projective varieties]], the singularities are the points where the [[Jacobian matrix]] has a [[rank (linear algebra)|rank]] which is lower than at other points of the variety.
 +
 +
For affine and projective varieties, the singularities are the points where the Jacobian matrix has a rank which is lower than at other points of the variety.
 +
 +
对于仿射变种和射影变种，奇异点是指雅可比矩阵的秩低于其它变种点的秩的点。
 +
 +
 +
 +
An equivalent definition in terms of [[commutative algebra]] may be given, which extends to [[abstract variety|abstract varieties]] and [[scheme (mathematics)|schemes]]: A point is ''singular'' if the [[Localization of a ring|local ring at this point]] is not a [[regular local ring]].
 +
 +
An equivalent definition in terms of commutative algebra may be given, which extends to abstract varieties and schemes: A point is singular if the local ring at this point is not a regular local ring.
 +
 +
可以给出一个关于交换代数的等价定义，它扩展到抽象的簇和方案: 如果局部环在这一点上不是一个正则局部环，那么一个点就是奇异的。
 +
 +
 +
 +
==See also==
 +
 +
*[[Catastrophe theory]]
 +
 +
*[[Defined and undefined]]
 +
 +
*[[Degeneracy (mathematics)]]
 +
 +
*[[Division by zero]]
 +
 +
*[[Hyperbolic growth]]
 +
 +
*[[Pathological (mathematics)]]
 +
 +
*[[Singular solution]]
 +
 +
*[[Removable singularity]]
 +
 +
 +
 +
==References==
 +
 +
{{Reflist}}
 +
 +
 +
 +
{{Authority control}}
 +
  
  
 +
[[Category:Mathematical analysis]]
  
 
Category:Mathematical analysis
 
Category:Mathematical analysis

2020年10月27日 (二) 22:17的版本

此词条暂由彩云小译翻译，翻译字数共1231，未经人工整理和审校，带来阅读不便，请见谅。

In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point where the mathematical object ceases to be well-behaved in some particular way, such as the lack of differentiability or analyticity.[1][2][3][4]

In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point where the mathematical object ceases to be well-behaved in some particular way, such as the lack of differentiability or analyticity.

在数学中，奇点通常是一个给定的数学对象没有定义的点，或者是一个数学对象不再以某种特定方式表现良好的点，例如缺乏可微性或分析性。


For example, the real function

For example, the real function

例如，真正的函数


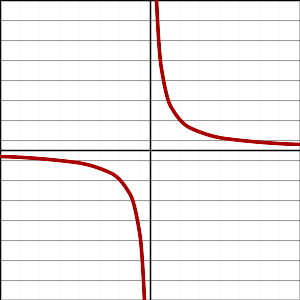
[math]\displaystyle{ f(x)=\frac{1}{x} }[/math]

[math]\displaystyle{ f(x)=\frac{1}{x} }[/math]

= frac {1}{ x } </math >


has a singularity at [math]\displaystyle{ x = 0 }[/math], where it seems to "explode" to [math]\displaystyle{ \pm\infty }[/math] and is hence not defined. The absolute value function [math]\displaystyle{ g(x) = |x| }[/math] also has a singularity at x = 0, since it is not differentiable there.[1][5]

has a singularity at [math]\displaystyle{ x = 0 }[/math], where it seems to "explode" to [math]\displaystyle{ \pm\infty }[/math] and is hence not defined. The absolute value function [math]\displaystyle{ g(x) = |x| }[/math] also has a singularity at , since it is not differentiable there.

有一个奇点在 < math > x = 0 </math > ，它似乎“爆炸”到 < math > pm infty </math > ，因此没有定义。绝对值函数 < math > g (x) = | x | </math > 也有一个奇点，因为它在那里是不可微的。


The algebraic curve defined by [math]\displaystyle{ \{(x,y):y^3-x^2=0\} }[/math] in the [math]\displaystyle{ (x, y) }[/math] coordinate system has a singularity (called a cusp) at [math]\displaystyle{ (0, 0) }[/math]. For singularities in algebraic geometry, see singular point of an algebraic variety. For singularities in differential geometry, see singularity theory.

The algebraic curve defined by [math]\displaystyle{ \{(x,y):y^3-x^2=0\} }[/math] in the [math]\displaystyle{ (x, y) }[/math] coordinate system has a singularity (called a cusp) at [math]\displaystyle{ (0, 0) }[/math]. For singularities in algebraic geometry, see singular point of an algebraic variety. For singularities in differential geometry, see singularity theory.

代数曲线定义于 math > (x，y) : y ^ 3-x ^ 2 = 0} </math > (x，y) </math > 坐标系在 math > (0,0) </math > 上有一个奇点(叫做尖点)。关于代数几何的奇点，请参阅《非奇异。关于微分几何的奇点，请参阅《奇点理论。


Real analysis

In real analysis, singularities are either discontinuities, or discontinuities of the derivative (sometimes also discontinuities of higher order derivatives). There are four kinds of discontinuities: type I, which has two subtypes, and type II, which can also be divided into two subtypes (though usually is not).

In real analysis, singularities are either discontinuities, or discontinuities of the derivative (sometimes also discontinuities of higher order derivatives). There are four kinds of discontinuities: type I, which has two subtypes, and type II, which can also be divided into two subtypes (though usually is not).

在实际分析中，奇点要么是导数的不连续性，要么是导数的不连续性(有时也是高阶导数的不连续性)。有四种不连续性: i 型(有两个子类型)和 II 型(也可以分为两个子类型(虽然通常不是)。


To describe the way these two types of limits are being used, suppose that [math]\displaystyle{ f(x) }[/math] is a function of a real argument [math]\displaystyle{ x }[/math], and for any value of its argument, say [math]\displaystyle{ c }[/math], then the left-handed limit, [math]\displaystyle{ f(c^-) }[/math], and the right-handed limit, [math]\displaystyle{ f(c^+) }[/math], are defined by:

To describe the way these two types of limits are being used, suppose that [math]\displaystyle{ f(x) }[/math] is a function of a real argument [math]\displaystyle{ x }[/math], and for any value of its argument, say [math]\displaystyle{ c }[/math], then the left-handed limit, [math]\displaystyle{ f(c^-) }[/math], and the right-handed limit, [math]\displaystyle{ f(c^+) }[/math], are defined by:

为了描述这两种类型的限制被使用的方式，假设 < math > f (x) </math > 是一个实参数的函数 < math > x </math > ，并且对于它的参数的任何值，比如 < math > c </math > ，那么左手限制 < math > f (c ^ -) </math > ，和右手限制 < math > f (c ^ +) </math，定义为:

[math]\displaystyle{ f(c^-) = \lim_{x \to c}f(x) }[/math], constrained by [math]\displaystyle{ x \lt c }[/math] and

[math]\displaystyle{ f(c^-) = \lim_{x \to c}f(x) }[/math], constrained by [math]\displaystyle{ x \lt c }[/math] and

[ math > f (c ^ -) = lim _ { x to c } f (x) </math > ，受到 < math > x </math > 和 </math > 的约束


[math]\displaystyle{ f(c^+) = \lim_{x \to c}f(x) }[/math], constrained by [math]\displaystyle{ x \gt c }[/math].

[math]\displaystyle{ f(c^+) = \lim_{x \to c}f(x) }[/math], constrained by [math]\displaystyle{ x \gt c }[/math].

[ math > f (c ^ +) = lim _ { x to c } f (x) </math > ，受 < math > x > c </math > 约束。


The value [math]\displaystyle{ f(c^-) }[/math] is the value that the function [math]\displaystyle{ f(x) }[/math] tends towards as the value [math]\displaystyle{ x }[/math] approaches [math]\displaystyle{ c }[/math] from below, and the value [math]\displaystyle{ f(c^+) }[/math] is the value that the function [math]\displaystyle{ f(x) }[/math] tends towards as the value [math]\displaystyle{ x }[/math] approaches [math]\displaystyle{ c }[/math] from above, regardless of the actual value the function has at the point where [math]\displaystyle{ x = c }[/math] .

The value [math]\displaystyle{ f(c^-) }[/math] is the value that the function [math]\displaystyle{ f(x) }[/math] tends towards as the value [math]\displaystyle{ x }[/math] approaches [math]\displaystyle{ c }[/math] from below, and the value [math]\displaystyle{ f(c^+) }[/math] is the value that the function [math]\displaystyle{ f(x) }[/math] tends towards as the value [math]\displaystyle{ x }[/math] approaches [math]\displaystyle{ c }[/math] from above, regardless of the actual value the function has at the point where [math]\displaystyle{ x = c }[/math] .

值 < math > f (c ^ -) </math > 是函数 < math > f (x) </math > 趋向于下面的值 < math > x </math > 接近 < math > c </math > ，值 < math > f (c ^ +) </math > 是函数 < math > f (x) </math > 趋向于上面的值 < math > x </math > 接近 math > c </math > ，而不管函数在数学上的实际值 < x = c </math > 。


There are some functions for which these limits do not exist at all. For example, the function

There are some functions for which these limits do not exist at all. For example, the function

有些函数根本不存在这些限制。例如，函数

[math]\displaystyle{ g(x) = \sin\left(\frac{1}{x}\right) }[/math]

[math]\displaystyle{ g(x) = \sin\left(\frac{1}{x}\right) }[/math]

< math > g (x) = sin left (frac {1}{ x } right) </math >

does not tend towards anything as [math]\displaystyle{ x }[/math] approaches [math]\displaystyle{ c = 0 }[/math]. The limits in this case are not infinite, but rather undefined: there is no value that [math]\displaystyle{ g(x) }[/math] settles in on. Borrowing from complex analysis, this is sometimes called an essential singularity.

does not tend towards anything as [math]\displaystyle{ x }[/math] approaches [math]\displaystyle{ c = 0 }[/math]. The limits in this case are not infinite, but rather undefined: there is no value that [math]\displaystyle{ g(x) }[/math] settles in on. Borrowing from complex analysis, this is sometimes called an essential singularity.

不倾向于做任何事情，因为。在这种情况下，限制不是无限的，而是未定义的: 没有一个值是 < math > g (x) </math > 的。借用复杂的分析，这有时被称为本质奇点。


The possible cases at a given value [math]\displaystyle{ c }[/math] for the argument are as follows.

The possible cases at a given value [math]\displaystyle{ c }[/math] for the argument are as follows.

参数在给定值 < math > c </math > 下的可能情况如下。

  • A point of continuity is a value of [math]\displaystyle{ c }[/math] for which [math]\displaystyle{ f(c^-) = f(c) = f(c^+) }[/math], as one expects for a smooth function. All the values must be finite. If [math]\displaystyle{ c }[/math] is not a point of continuity, then a discontinuity occurs at [math]\displaystyle{ c }[/math].
  • A type I discontinuity occurs when both [math]\displaystyle{ f(c^-) }[/math] and [math]\displaystyle{ f(c^+) }[/math] exist and are finite, but at least one of the following three conditions also applies:
    • [math]\displaystyle{ f(c^-) \neq f(c^+) }[/math];
    • [math]\displaystyle{ f(x) }[/math] is not defined for the case of [math]\displaystyle{ x = c }[/math]; or
    • [math]\displaystyle{ f(c) }[/math] has a defined value, which, however, does not match the value of the two limits.
Type I discontinuities can be further distinguished as being one of the following subtypes:

Type I discontinuities can be further distinguished as being one of the following subtypes:

第一类不连续性可以进一步区分为下列子类型之一:

  • A jump discontinuity occurs when [math]\displaystyle{ f(c^-) \neq f(c^+) }[/math], regardless of whether [math]\displaystyle{ f(c) }[/math] is defined, and regardless of its value if it is defined.
  • A jump discontinuity occurs when [math]\displaystyle{ f(c^-) \neq f(c^+) }[/math], regardless of whether [math]\displaystyle{ f(c) }[/math] is defined, and regardless of its value if it is defined.
  • 当 < math > f (c ^ -) neq f (c ^ +) </math > ，不管 < math > f (c) </math > 是否定义，也不管是否定义了它的值时，就会发生跳转不连续性。
  • A removable discontinuity occurs when [math]\displaystyle{ f(c^-) = f(c^+) }[/math], also regardless of whether [math]\displaystyle{ f(c) }[/math] is defined, and regardless of its value if it is defined (but which does not match that of the two limits).
  • A removable discontinuity occurs when [math]\displaystyle{ f(c^-) = f(c^+) }[/math], also regardless of whether [math]\displaystyle{ f(c) }[/math] is defined, and regardless of its value if it is defined (but which does not match that of the two limits).
  • 当 < math > f (c ^ -) = f (c ^ +) </math > ，也不管 < math > f (c) </math > 是否已定义，也不管是否已定义它的值(但不匹配两个极限)时，就会出现可移动的不连续性。
  • A type II discontinuity occurs when either [math]\displaystyle{ f(c^-) }[/math] or [math]\displaystyle{ f(c^+) }[/math] does not exist (possibly both). This has two subtypes, which are usually not considered separately:
    • An infinite discontinuity is the special case when either the left hand or right hand limit does not exist, specifically because it is infinite, and the other limit is either also infinite, or is some well defined finite number. In other words, the function has an infinite discontinuity when its graph has a vertical asymptote.
    • An essential singularity is a term borrowed from complex analysis (see below). This is the case when either one or the other limits [math]\displaystyle{ f(c^-) }[/math] or [math]\displaystyle{ f(c^+) }[/math] does not exist, but not because it is an infinite discontinuity. Essential singularities approach no limit, not even if valid answers are extended to include [math]\displaystyle{ \pm\infty }[/math].


In real analysis, a singularity or discontinuity is a property of a function alone. Any singularities that may exist in the derivative of a function are considered as belonging to the derivative, not to the original function.

In real analysis, a singularity or discontinuity is a property of a function alone. Any singularities that may exist in the derivative of a function are considered as belonging to the derivative, not to the original function.

在实际分析中，奇点或不连续是函数本身的一个性质。任何可能存在于函数导数中的奇点都被认为是属于导数，而不是原函数。


Coordinate singularities

Main article: Coordinate singularity

A coordinate singularity occurs when an apparent singularity or discontinuity occurs in one coordinate frame, which can be removed by choosing a different frame. An example of this is the apparent singularity at the 90 degree latitude in spherical coordinates. An object moving due north (for example, along the line 0 degrees longitude) on the surface of a sphere will suddenly experience an instantaneous change in longitude at the pole (in the case of the example, jumping from longitude 0 to longitude 180 degrees). This discontinuity, however, is only apparent; it is an artifact of the coordinate system chosen, which is singular at the poles. A different coordinate system would eliminate the apparent discontinuity (e.g., by replacing the latitude/longitude representation with an n-vector representation).

A coordinate singularity occurs when an apparent singularity or discontinuity occurs in one coordinate frame, which can be removed by choosing a different frame. An example of this is the apparent singularity at the 90 degree latitude in spherical coordinates. An object moving due north (for example, along the line 0 degrees longitude) on the surface of a sphere will suddenly experience an instantaneous change in longitude at the pole (in the case of the example, jumping from longitude 0 to longitude 180 degrees). This discontinuity, however, is only apparent; it is an artifact of the coordinate system chosen, which is singular at the poles. A different coordinate system would eliminate the apparent discontinuity (e.g., by replacing the latitude/longitude representation with an -vector representation).

当在一个坐标系中出现明显的奇异或不连续时，就会出现坐标奇异性，这可以通过选择不同的坐标系来消除。这方面的一个例子是球坐标系中90度纬度处的明显奇点。在球体表面向北移动的物体(例如，沿着0度经线)在极点会突然经历经度的瞬时变化(例如，从0度经度跳到180度经度)。然而，这种不连续性只是显而易见的，它是所选择的坐标系的人工制品，在极点是奇异的。不同的坐标系将消除明显的不连续性(例如，将纬度/经度表示替换为-vector 表示)。


Complex analysis

In complex analysis, there are several classes of singularities. These include the isolated singularities, the nonisolated singularities and the branch points.

In complex analysis, there are several classes of singularities. These include the isolated singularities, the nonisolated singularities and the branch points.

在复分析中，有几类奇异点。其中包括孤立奇点、非孤立奇点和分支点。


Isolated singularities

Suppose that U is an open subset of the complex numbers C, with the point a being an element of U, and that f is a complex differentiable function defined on some neighborhood around a, excluding a: U \ {a}, then:

Suppose that U is an open subset of the complex numbers C, with the point a being an element of U, and that f is a complex differentiable function defined on some neighborhood around a, excluding a: U \ {a}, then:

假设 u 是复数 c 的一个开子集，点 a 是 u 的一个元素，而 f 是定义在 a 周围某个邻域上的复可微函数，除了 a: u { a } ，那么:

  • The point a is a pole or non-essential singularity of f if there exists a holomorphic function g defined on U with g(a) nonzero, and a natural number n such that f(z) = g(z) / (z − a)n for all z in U \ {a}. The least such number n is called the order of the pole. The derivative at a non-essential singularity itself has a non-essential singularity, with n increased by 1 (except if n is 0 so that the singularity is removable).


Nonisolated singularities

Other than isolated singularities, complex functions of one variable may exhibit other singular behaviour. These are termed nonisolated singularities, of which there are two types:

Other than isolated singularities, complex functions of one variable may exhibit other singular behaviour. These are termed nonisolated singularities, of which there are two types:

除孤立奇点外，一个变量的复变函数还可能表现出其他奇异行为。这些称为非孤立奇点，其中有两种类型:


  • Cluster points: limit points of isolated singularities. If they are all poles, despite admitting Laurent series expansions on each of them, then no such expansion is possible at its limit.
  • Natural boundaries: any non-isolated set (e.g. a curve) on which functions cannot be analytically continued around (or outside them if they are closed curves in the Riemann sphere).


Branch points

Branch points are generally the result of a multi-valued function, such as [math]\displaystyle{ \sqrt{z} }[/math] or [math]\displaystyle{ \log(z) }[/math], which are defined within a certain limited domain so that the function can be made single-valued within the domain. The cut is a line or curve excluded from the domain to introduce a technical separation between discontinuous values of the function. When the cut is genuinely required, the function will have distinctly different values on each side of the branch cut. The shape of the branch cut is a matter of choice, even though it must connect two different branch points (such as [math]\displaystyle{ z=0 }[/math] and [math]\displaystyle{ z=\infty }[/math] for [math]\displaystyle{ \log(z) }[/math]) which are fixed in place.

Branch points are generally the result of a multi-valued function, such as [math]\displaystyle{ \sqrt{z} }[/math] or [math]\displaystyle{ \log(z) }[/math], which are defined within a certain limited domain so that the function can be made single-valued within the domain. The cut is a line or curve excluded from the domain to introduce a technical separation between discontinuous values of the function. When the cut is genuinely required, the function will have distinctly different values on each side of the branch cut. The shape of the branch cut is a matter of choice, even though it must connect two different branch points (such as [math]\displaystyle{ z=0 }[/math] and [math]\displaystyle{ z=\infty }[/math] for [math]\displaystyle{ \log(z) }[/math]) which are fixed in place.

分支点通常是多值函数的结果，比如 < math > sqrt { z } </math > 或 < math > log (z) </math > ，这些分支点定义在一个特定的有限域内，因此函数可以在域内成为单值函数。切割是一条从区域中排除的直线或曲线，用以在不连续的函数值之间进行技术上的分离。当切割是真正需要的，功能将有明显不同的价值观在每一侧的分支削减。分支切口的形状是一个选择问题，即使它必须连接两个不同的分支点(比如 < math > z = 0 </math > 和 < math > z = infty </math > ，用于 < math > log (z) </math >) ，这两个分支点是固定的。


Finite-time singularity

The reciprocal function, exhibiting hyperbolic growth.

The reciprocal function, exhibiting hyperbolic growth.

[[倒数函数，显示双曲增长。[] < ! -- 一个更好的图像应该是1/(1-x)或类似的图像，显示一个正的奇点，并且随着 x 的增加而增长 -- >


A finite-time singularity occurs when one input variable is time, and an output variable increases towards infinity at a finite time. These are important in kinematics and PDEs (Partial Differential Equations) – infinites do not occur physically, but the behavior near the singularity is often of interest. Mathematically, the simplest finite-time singularities are power laws for various exponents of the form [math]\displaystyle{ x^{-\alpha}, }[/math] of which the simplest is hyperbolic growth, where the exponent is (negative) 1: [math]\displaystyle{ x^{-1}. }[/math] More precisely, in order to get a singularity at positive time as time advances (so the output grows to infinity), one instead uses [math]\displaystyle{ (t_0-t)^{-\alpha} }[/math] (using t for time, reversing direction to [math]\displaystyle{ -t }[/math] so that time increases to infinity, and shifting the singularity forward from 0 to a fixed time [math]\displaystyle{ t_0 }[/math]).

A finite-time singularity occurs when one input variable is time, and an output variable increases towards infinity at a finite time. These are important in kinematics and PDEs (Partial Differential Equations) – infinites do not occur physically, but the behavior near the singularity is often of interest. Mathematically, the simplest finite-time singularities are power laws for various exponents of the form [math]\displaystyle{ x^{-\alpha}, }[/math] of which the simplest is hyperbolic growth, where the exponent is (negative) 1: [math]\displaystyle{ x^{-1}. }[/math] More precisely, in order to get a singularity at positive time as time advances (so the output grows to infinity), one instead uses [math]\displaystyle{ (t_0-t)^{-\alpha} }[/math] (using t for time, reversing direction to [math]\displaystyle{ -t }[/math] so that time increases to infinity, and shifting the singularity forward from 0 to a fixed time [math]\displaystyle{ t_0 }[/math]).

当输入变量为时间，输出变量在有限时间内向无穷大方向增长时，出现有限时间奇异性。这些在运动学和偏微分方程(偏微分方程)中都很重要——物理上不存在无穷大，但奇点附近的行为通常是有趣的。数学上，最简单的有限时间奇点是形式为 < math > x ^ {-alpha }的各种指数的幂律，其中最简单的是双曲增长，其指数是(负)1: < math > x ^ {-1}。更准确地说，为了在正时间得到一个奇点，随着时间的推移(所以输出增加到无穷大) ，一个代替使用 < math > (t _ 0-t) ^ {-alpha } </math > (使用 t 表示时间，倒转方向到 < math >-t </math > ，所以时间增加到无穷大，并将奇点从0向前移动到一个固定的时间 < t _ 0 </math >)。


An example would be the bouncing motion of an inelastic ball on a plane. If idealized motion is considered, in which the same fraction of kinetic energy is lost on each bounce, the frequency of bounces becomes infinite, as the ball comes to rest in a finite time. Other examples of finite-time singularities include the various forms of the Painlevé paradox (for example, the tendency of a chalk to skip when dragged across a blackboard), and how the precession rate of a coin spun on a flat surface accelerates towards infinite—before abruptly stopping (as studied using the Euler's Disk toy).

An example would be the bouncing motion of an inelastic ball on a plane. If idealized motion is considered, in which the same fraction of kinetic energy is lost on each bounce, the frequency of bounces becomes infinite, as the ball comes to rest in a finite time. Other examples of finite-time singularities include the various forms of the Painlevé paradox (for example, the tendency of a chalk to skip when dragged across a blackboard), and how the precession rate of a coin spun on a flat surface accelerates towards infinite—before abruptly stopping (as studied using the Euler's Disk toy).

一个例子是一个非弹性球在平面上的反弹运动。如果考虑理想运动，即每次弹跳都损失相同的动能，那么弹跳的频率就是无限的，因为球停在一个有限的时间里。有限时间奇点的其他例子包括各种形式的 painlevé 悖论(例如，粉笔在黑板上拖动时会跳过) ，以及在平面上旋转的硬币的进动速率如何加速到无限，然后突然停止(用欧拉圆盘玩具进行的研究)。


Hypothetical examples include Heinz von Foerster's facetious "Doomsday's equation" (simplistic models yield infinite human population in finite time).

Hypothetical examples include Heinz von Foerster's facetious "Doomsday's equation" (simplistic models yield infinite human population in finite time).

假设的例子包括 Heinz von Foerster 滑稽的“末日方程”(简单化的模型在有限的时间里产生无限的人口)。


Algebraic geometry and commutative algebra

In algebraic geometry, a singularity of an algebraic variety is a point of the variety where the tangent space may not be regularly defined. The simplest example of singularities are curves that cross themselves. But there are other types of singularities, like cusps. For example, the equation y模板:Sup − x模板:Sup = 0 defines a curve that has a cusp at the origin x = y = 0. One could define the x-axis as a tangent at this point, but this definition can not be the same as the definition at other points. In fact, in this case, the x-axis is a "double tangent."

In algebraic geometry, a singularity of an algebraic variety is a point of the variety where the tangent space may not be regularly defined. The simplest example of singularities are curves that cross themselves. But there are other types of singularities, like cusps. For example, the equation − x = 0 }} defines a curve that has a cusp at the origin . One could define the -axis as a tangent at this point, but this definition can not be the same as the definition at other points. In fact, in this case, the -axis is a "double tangent."

在代数几何中，代数簇的奇点是各种各样的切线空间可能没有规则定义的一点。奇点最简单的例子就是它们自己交叉的曲线。但是还有其他类型的奇点，比如尖点。例如，方程 -x = 0}}定义了一条在原点有尖点的曲线。可以将-轴定义为这一点的切线，但这个定义不能与其他点的定义相同。实际上，在这种情况下,-轴是一个“双切线”


For affine and projective varieties, the singularities are the points where the Jacobian matrix has a rank which is lower than at other points of the variety.

For affine and projective varieties, the singularities are the points where the Jacobian matrix has a rank which is lower than at other points of the variety.

对于仿射变种和射影变种，奇异点是指雅可比矩阵的秩低于其它变种点的秩的点。


An equivalent definition in terms of commutative algebra may be given, which extends to abstract varieties and schemes: A point is singular if the local ring at this point is not a regular local ring.

An equivalent definition in terms of commutative algebra may be given, which extends to abstract varieties and schemes: A point is singular if the local ring at this point is not a regular local ring.

可以给出一个关于交换代数的等价定义，它扩展到抽象的簇和方案: 如果局部环在这一点上不是一个正则局部环，那么一个点就是奇异的。


See also


References

  1. ↑ 1.0 1.1 "The Definitive Glossary of Higher Mathematical Jargon — Singularity". Math Vault (in English). 2019-08-01. Retrieved 2019-12-12.{{cite web}}: CS1 maint: url-status (link)
  2. ↑ 2.0 2.1 "Singularities, Zeros, and Poles". mathfaculty.fullerton.edu. Retrieved 2019-12-12.
  3. ↑ "Singularity | complex functions". Encyclopedia Britannica (in English). Retrieved 2019-12-12.
  4. ↑ "Singularity (mathematics)". TheFreeDictionary.com. Retrieved 2019-12-12.
  5. ↑ Berresford, Geoffrey C.; Rockett, Andrew M. (2015). Applied Calculus. Cengage Learning. p. 151. ISBN 978-1-305-46505-3. https://books.google.com/books?id=wzNBBAAAQBAJ&pg=PA151. 
  6. ↑ Weisstein, Eric W. "Singularity". mathworld.wolfram.com (in English). Retrieved 2019-12-12.

Category:Mathematical analysis

分类: 数学分析


This page was moved from wikipedia:en:Singularity (mathematics). Its edit history can be viewed at 奇点/edithistory

取自“https://wiki.swarma.org/index.php?title=奇点&oldid=17203”