“层次聚类”的版本间的差异
| 第64行: | 第64行: | ||
=== 连接准则 Linkage criteria=== | === 连接准则 Linkage criteria=== | ||
| − | + | 连接标准决定了集合内簇之间的距离作为两个簇之间距离的函数。簇''A''和簇''B''之间一些常用的连接标准如下:<ref>{{cite web | title=The CLUSTER Procedure: Clustering Methods |url=https://support.sas.com/documentation/cdl/en/statug/63033/HTML/default/statug_cluster_sect012.htm | work=SAS/STAT 9.2 Users Guide | publisher= [[SAS Institute]] | date= | accessdate=2009-04-26}}</ref><ref>{{cite journal |last=Székely |first=G. J. |last2=Rizzo |first2=M. L. |year=2005 |title=Hierarchical clustering via Joint Between-Within Distances: Extending Ward's Minimum Variance Method |journal=Journal of Classification |volume=22 |issue=2 |pages=151–183 |doi=10.1007/s00357-005-0012-9 }}</ref> | |
| − | |||
| − | |||
| − | |||
| − | |||
{|class="wikitable" | {|class="wikitable" | ||
| 第104行: | 第100行: | ||
* 在合并了两个簇之后,某个簇的定义符号(即为度量一个簇的质量而定义的一个量)的增量。<ref>Zhang, et al. "Agglomerative clustering via maximum incremental path integral." Pattern Recognition (2013).</ref><ref>Zhao, and Tang. "Cyclizing clusters via zeta function of a graph."Advances in Neural Information Processing Systems. 2008.</ref><ref>Ma, et al. "Segmentation of multivariate mixed data via lossy data coding and compression." IEEE Transactions on Pattern Analysis and Machine Intelligence, 29(9) (2007): 1546-1562.</ref> | * 在合并了两个簇之后,某个簇的定义符号(即为度量一个簇的质量而定义的一个量)的增量。<ref>Zhang, et al. "Agglomerative clustering via maximum incremental path integral." Pattern Recognition (2013).</ref><ref>Zhao, and Tang. "Cyclizing clusters via zeta function of a graph."Advances in Neural Information Processing Systems. 2008.</ref><ref>Ma, et al. "Segmentation of multivariate mixed data via lossy data coding and compression." IEEE Transactions on Pattern Analysis and Machine Intelligence, 29(9) (2007): 1546-1562.</ref> | ||
| − | |||
==讨论== | ==讨论== | ||
2020年10月29日 (四) 22:31的版本
此词条暂由水流心不竞翻译,未经审校,带来阅读不便,请见谅。由CecileLi初步审校。翻译评级:B
在数据挖掘和统计学中,层次聚类 Hierarchical clustering (HCA)(也被称为“层次数据聚类”)是一种通过建立一个集群层次结构来聚类分析的方法。实现层次聚类的方法通常有两种:[1]
- 凝聚聚类 Agglomerative:这是一种“自上而下又自下而上/纵向”的方法:每个被观察数据从自己的簇类中开始,当一个观察组数据向上层移动时,成对的簇类集群被合并。
- 分裂聚类 Divisive: 这是一种“自上而下”的方法:所有的被观察数据都从一个簇类集群中开始,当一个簇类向下移动时,整个观察组数据群会递归地执行分割。
一般来说,合并和分裂是基于贪心算法 greedy algorithm决定的。层次聚类的结果 [2] 通常在树状图中呈现。
层次凝聚聚类 Hierarchical agglomerative clustering(HAC)标准算法的时间复杂度为[math]\displaystyle{ \mathcal{O}(n^3) }[/math] ,并且需要 [math]\displaystyle{ \mathcal{O}(n^2) }[/math] 占用内存,这使得它对于中等数据集来说效率太低了。然而,对于某些特殊情况,已知的最有效凝聚方法(复杂度 [math]\displaystyle{ \mathcal{O}(n^2) }[/math])是: SLINK 用于单连接聚类 Single-linkage clustering[3], CLINK用于完全连接 complete-linkage clustering[4]。一般情况下的运行时可以缩减为[math]\displaystyle{ \mathcal{O}(n^2 \log n) }[/math] ,代价是进一步增加内存需求。在多数情况下,这种方法的内存消耗太大,并不实用。
除了单连接的特殊情况外,所有算法(除了时间复杂度为[math]\displaystyle{ \mathcal{O}(2^n) }[/math]的全局搜索 exhaustive search)都不能保证找到最优解。
分裂聚类全局搜索的时间复杂度为[math]\displaystyle{ \mathcal{O}(2^n) }[/math],但通常使用更快的启发式 heuristics来选择分裂,比如k-means。
簇异性 Cluster dissimilarity
为了决定哪些簇应该被组合起来(用于聚合) ,或者哪些簇应该被分离(用于分裂) ,测量簇之间的相异度 dissimilarity。在大多数层次聚类方法中,这是通过使用适当的度量 metric(对两个簇之间的距离度量)和连接准则来实现的。连接标准决定了两个簇之间的距离函数。
度量标准 Metric
更多信息请查看度量标准 Metric
度量方式的选择将影响数据簇类的形状,因为某些元素依据一个距离可能彼此接近,而依据另一个距离可能彼此远离。例如,在一个二维空间中,点(1,0)和原点(0,0)之间的距离通常是1,但是点(1,1)和原点(0,0)之间的距离在曼哈顿距离下可以是2,在欧几里得度量下可以是 [math]\displaystyle{ \scriptstyle\sqrt{2} }[/math],在最大距离下可以是1。
一些常用的指标如下:[5]
| 名字 | 公式 |
|---|---|
| 欧氏距离 Euclidean distance | [math]\displaystyle{ \|a-b \|_2 = \sqrt{\sum_i (a_i-b_i)^2} }[/math] |
| 平方欧氏距离 Squared Euclidean distance | [math]\displaystyle{ \|a-b \|_2^2 = \sum_i (a_i-b_i)^2 }[/math] |
| 曼哈顿距离 Manhattan distance | [math]\displaystyle{ \|a-b \|_1 = \sum_i |a_i-b_i| }[/math] |
| 最大距离 Maximum distance | [math]\displaystyle{ \|a-b \|_\infty = \max_i |a_i-b_i| }[/math] |
| 马氏距离 Mahalanobis distance | [math]\displaystyle{ \sqrt{(a-b)^{\top}S^{-1}(a-b)} }[/math] 其中S是协方差矩阵 |
对于文本文字或其他非数字数据,常常使用汉明距离 Hamming distance或编辑距离 Levenshtein distance等度量标准。
通过对数据聚类健康心理学研究的回顾发现,在该研究领域已发表的研究中,最常见的距离测量方法是欧氏距离或平方欧氏距离。[citation needed]
连接准则 Linkage criteria
连接标准决定了集合内簇之间的距离作为两个簇之间距离的函数。簇A和簇B之间一些常用的连接标准如下:[6][7]
| 名字 | 公式 |
|---|---|
| 最大或完全连接聚类 | [math]\displaystyle{ \max \, \{\, d(a,b) : a \in A,\, b \in B \,\} }[/math] |
| 最小或单连接聚类 | [math]\displaystyle{ \min \, \{\, d(a,b) : a \in A,\, b \in B \,\} }[/math] |
| 未加权平均连接聚类 Unweighted average linkage clustering (或UPGMA) | [math]\displaystyle{ \frac{1}{|A|\cdot|B|} \sum_{a \in A }\sum_{ b \in B} d(a,b) }[/math] |
| 加权平均数连接聚类 Weighted average linkage clustering (或WPGMA) | [math]\displaystyle{ d(i \cup j, k) = \frac{d(i, k) + d(j, k)}{2} |- | 质心连接集群 Centroid linkage clustering (或UPGMC) | \lt math\gt \|c_s - c_t \| }[/math] where [math]\displaystyle{ c_s }[/math] and [math]\displaystyle{ c_t }[/math] 分别是 s类和 t类的中心. |
| 最小能量聚类Minimum energy clustering | [math]\displaystyle{ \frac {2}{nm}\sum_{i,j=1}^{n,m} \|a_i- b_j\|_2 - \frac {1}{n^2}\sum_{i,j=1}^{n} \|a_i-a_j\|_2 - \frac{1}{m^2}\sum_{i,j=1}^{m} \|b_i-b_j\|_2 }[/math] |
其中 d 是选定的度量单位。其他连接准则包括:
- 簇内方差之和。
- 候选簇从同一分布函数(V-连接 V-linkage)衍生的概率。
- k-最近邻 k-nearest-neighbour图 (KNN,图度连接)上的入度与出度的乘积[9]
讨论
层次聚类具有明显的优势,它可以使用任何有效的距离度量。事实上,观测本身也并不是必需的,层次聚类所需要用的只是一个距离矩阵。
凝聚聚类实例
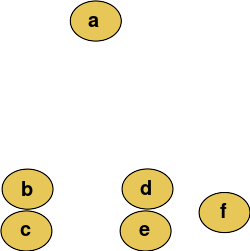
例如,假设要对这些数据进行聚类,将欧式距离作为度量。系统聚类树状图如下:
Cutting the tree at a given height will give a partitioning clustering at a selected precision. In this example, cutting after the second row (from the top) of the dendrogram will yield clusters {a} {b c} {d e} {f}. Cutting after the third row will yield clusters {a} {b c} {d e f}, which is a coarser clustering, with a smaller number but larger clusters.
在给定的高度切割树状图中,将以选定的精度提供分区聚类。在这个示例中,在树状图的第二行(从顶部开始)之后切割将产生类别{a} {b c} {d e} {f}。在第三行之后进行切割将产生类别{a} {b c} {d e f},这是一个较为粗略的聚类,其数量少但簇群较大。
此方法通过逐步合并簇,从单个元素构建层次结构。在我们的示例中,有六个元素{a} {b} {c} {d} {e}和{f}。第一步是确定在集群中合并哪些元素。通常,我们希望根据选定的距离获取两个最接近的元素。
还可以选择在这个阶段构造一个距离矩阵 distance matrix,其中第i行第j列中的数字是 i和j,即为两个元素之间的距离。然后,随着聚类过程的推进,行和列随着聚类的合并和距离的更新而合并。这是实现这类聚类的常用方法,并且具有缓存簇之间的距离的优点。在单连接聚类 single-linkage clustering页面中描述了一个简单的凝聚聚类算法; 它适用于很多连接(见下文)。
假设我们已经合并了两个最接近的元素 b 和c,现在我们有以下簇{a}, {b, c}, {d}, {e} 和{f} ,并希望进一步合并它们。为此,我们需要计算{a} 和 {b c}之间的距离,从而定义两个簇之间的距离。
通常情况下的簇[math]\displaystyle{ \mathcal{A} }[/math]和 簇[math]\displaystyle{ \mathcal{B} }[/math]之间距离如下:
- 每个簇内元素之间的最大距离(又名完全连接聚类 complete-linkage clustering)
- [math]\displaystyle{ \max \{\, d(x,y) : x \in \mathcal{A},\, y \in \mathcal{B}\,\}. }[/math]
- 每个簇内的元素之间的最小距离(也称为单连接聚类 single-linkage clustering):
- [math]\displaystyle{ \min \{\, d(x,y) : x \in \mathcal{A},\, y \in \mathcal{B} \,\}. }[/math]
- 每个簇元素之间的平均距离(也称为平均连接聚类,UPGMA):
- [math]\displaystyle{ {1 \over {|\mathcal{A}|\cdot|\mathcal{B}|}}\sum_{x \in \mathcal{A}}\sum_{ y \in \mathcal{B}} d(x,y). }[/math]
- 所有簇内元素方差之和。
- 候选簇从同一分布函数(V-连接 V-linkage)衍生的概率。
在采用最小距离的情况下,随机选择一对元素,从而能够生成几个结构上不同的树状图。或者,同时连接所有绑定对,生成唯一的树状图。[13]
当簇数足够少时,人们可以停止聚类过程。有些联系也可能保证聚集发生在比先前聚集更大的聚集距离上,直到当聚集距离太远无法合并时可以停止聚集(距离标准)。然而也有例外,如采用质心连接,可能会发生逆转(反转 inversions,偏离超节拍 departures from ultrametricity)[14]。
分裂聚类 Divisive clustering
分裂聚类的基本原理被公布为分裂分析聚类 DIvisive ANAlysis Clustering,(DIANA)算法[15]。最初,所有数据都位于同一个集群中,然后最大的集群被拆分,依此类推,直到每个元素都是独立的。
由于每个聚类存在[math]\displaystyle{ O(2^n) }[/math]种划分方法,所以需要启发式算法。DIANA 选择平均相异度最大的对象,然后将所有对象移动到与新集群更相似的集群中。
软件
开源工具

- ALGLIB implements several hierarchical clustering algorithms (single-link, complete-link, Ward) in C++ and C# with O(n²) memory and O(n³) run time.
- ALGLIB在C++ 和 C# 上以 [math]\displaystyle{ \mathcal{O}(2^n) }[/math] 的内存和 [math]\displaystyle{ \mathcal{O}(3^n) }[/math]的运行时间实现了几个层次聚类算法(单链接,完整链接,均值)。
- ELKI includes multiple hierarchical clustering algorithms, various linkage strategies and also includes the efficient SLINK,[3] CLINK[4] and Anderberg algorithms, flexible cluster extraction from dendrograms and various other cluster analysis algorithms.
- ELKI包括多种层次聚类算法,各种链接策略,同时包括高效运行,[3] CLINK[4] 安德伯格算法,从树状图和其他各种聚类分析算法中进行灵活的聚类提取。
- Octave, the GNU analog to MATLAB implements hierarchical clustering in function "linkage".
- Octave,与MATLAB类似的GNU在“联动”功能中实现了分层聚类。
- Orange, a data mining software suite, includes hierarchical clustering with interactive dendrogram visualisation.
- Orange,一个数据挖掘软件套件,包括层次聚类和交互式可视化树形图。
- R has many packages that provide functions for hierarchical clustering.
- R 有许多提供分层聚类功能的工具包。
- SciPy implements hierarchical clustering in Python, including the efficient SLINK algorithm.
- SciPy在python中实现分层聚类,包括高效的slink算法。
- scikit-learn also implements hierarchical clustering in Python.
- scikit-learn还实现了Python中的层次聚类。
- Weka includes hierarchical cluster analysis.
- Weka 包括层次聚类分析。
收费软件
- MATLAB 包括层次聚类分析。
- SAS PROC CLUSTER中包括层次聚类分析。
- SAS包括在群聚程序中进行层次聚类分析。
- Mathematica 包括层次聚类分析工具包。
- NCSS 包括层次聚类分析。
- SPSS包括层次聚类分析。
- QlucoreOmits 资源管理器包括层次聚类分析。
- Stata 包括层次聚类分析。
- CrimeStat 包括一个能够为地理位置提供图形输出的最近邻层次聚类算法。
参见
- 二进制空间划分 Binary space partitioning
- 层次包围盒 Bounding volume hierarchy
- 布朗群集 Brown clustering
- 遗传分类学 Cladistics
- 聚类分析 Cluster analysis
- 计算系统发生学 Computational phylogenetics
- CURE数据聚类算法 CURE data clustering algorithm
- Dasgupta的目标
- 树状图 Dendrogram
- 确定数据集中的簇数 Determining the number of clusters in a data set
- 网络层次聚类 Hierarchical clustering of networks
- 局部敏感哈希(LSH)方法 Locality-sensitive hashing
- 最近邻搜索 Nearest neighbor search
- 最近邻链算法 Nearest-neighbor chain algorithm
- 数值分类法 Numerical taxonomy
- OPTICS算法 OPTICS algorithm
- 统计距离 Statistical distance
- 持续同调 Persistent homology
参考文献
- ↑ Rokach, Lior, and Oded Maimon. "Clustering methods." Data mining and knowledge discovery handbook. Springer US, 2005. 321-352.
- ↑ Frank Nielsen (2016). "Chapter 8: Hierarchical Clustering". Introduction to HPC with MPI for Data Science. Springer. https://www.researchgate.net/publication/314700681.
- ↑ 3.0 3.1 3.2 R. Sibson (1973). "SLINK: an optimally efficient algorithm for the single-link cluster method" (PDF). The Computer Journal. British Computer Society. 16 (1): 30–34. doi:10.1093/comjnl/16.1.30.
- ↑ 4.0 4.1 4.2 D. Defays (1977). "An efficient algorithm for a complete-link method". The Computer Journal. British Computer Society. 20 (4): 364–366. doi:10.1093/comjnl/20.4.364.
- ↑ "The DISTANCE Procedure: Proximity Measures". SAS/STAT 9.2 Users Guide. SAS Institute. Retrieved 2009-04-26.
- ↑ "The CLUSTER Procedure: Clustering Methods". SAS/STAT 9.2 Users Guide. SAS Institute. Retrieved 2009-04-26.
- ↑ Székely, G. J.; Rizzo, M. L. (2005). "Hierarchical clustering via Joint Between-Within Distances: Extending Ward's Minimum Variance Method". Journal of Classification. 22 (2): 151–183. doi:10.1007/s00357-005-0012-9.
- ↑ 8.0 8.1 Ward, Joe H. (1963). "Hierarchical Grouping to Optimize an Objective Function". Journal of the American Statistical Association. 58 (301): 236–244. doi:10.2307/2282967.
- ↑ Zhang, Wei; Wang, Xiaogang; Zhao, Deli; Tang, Xiaoou (2012). Fitzgibbon, Andrew; Lazebnik, Svetlana; Perona, Pietro; Sato, Yoichi; Schmid, Cordelia (eds.). "Graph Degree Linkage: Agglomerative Clustering on a Directed Graph". Computer Vision – ECCV 2012. Lecture Notes in Computer Science (in English). Springer Berlin Heidelberg. 7572: 428–441. arXiv:1208.5092. Bibcode:2012arXiv1208.5092Z. doi:10.1007/978-3-642-33718-5_31. ISBN 9783642337185. 见: https://github.com/waynezhanghk/gacluster
- ↑ Zhang, et al. "Agglomerative clustering via maximum incremental path integral." Pattern Recognition (2013).
- ↑ Zhao, and Tang. "Cyclizing clusters via zeta function of a graph."Advances in Neural Information Processing Systems. 2008.
- ↑ Ma, et al. "Segmentation of multivariate mixed data via lossy data coding and compression." IEEE Transactions on Pattern Analysis and Machine Intelligence, 29(9) (2007): 1546-1562.
- ↑ Fernández, Alberto; Gómez, Sergio (2008). "Solving Non-uniqueness in Agglomerative Hierarchical Clustering Using Multidendrograms". Journal of Classification. 25 (1): 43–65. arXiv:cs/0608049. doi:10.1007/s00357-008-9004-x.
- ↑ Legendre, P.; Legendre, L. (2003). Numerical Ecology. Elsevier Science BV.
- ↑ Kaufman, L., & Roussew, P. J. (1990). Finding Groups in Data - An Introduction to Cluster Analysis. A Wiley-Science Publication John Wiley & Sons.
进一步阅读
- Kaufman, L.; Rousseeuw, P.J. (1990). Finding Groups in Data: An Introduction to Cluster Analysis (1 ed.). New York: John Wiley. ISBN 0-471-87876-6. https://archive.org/details/findinggroupsind00kauf.
- Hastie, Trevor; Tibshirani, Robert; Friedman, Jerome (2009). "14.3.12 Hierarchical clustering". The Elements of Statistical Learning (2nd ed.). New York: Springer. pp. 520–528. ISBN 978-0-387-84857-0. Archived from the original on 2009-11-10. http://www-stat.stanford.edu/~tibs/ElemStatLearn/. Retrieved 2009-10-20.