“复杂系统生物学”的版本间的差异

2020年11月3日 (二) 15:09的版本

复杂系统生物学 Complex system biology （CSB）是数学和理论生物学的一个分支或子领域，研究生物有机体结构和功能的复杂性，以及生物和物种的出现与进化，重点研究生物网络及其内部的复杂相互作用，以及生命所必须的基本关系与关系模式。因此，CBS是一个旨在发现和建模生命所必需的关系模式理论科学领域，它只与复杂系统理论和被称为系统生物学的生物学的系统方法有部分重叠;这是因为后者主要局限于生物组织和有机体的简化模型，以及对与生物学复杂性相关的哲学或语义问题的一般性考虑。此外，人们把广泛的抽象理论复杂系统作为应用数学的一个领域进行研究，无论其是否与生物学、化学或物理相关。

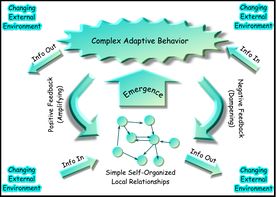
Network Representation of a Complex Adaptive System

一个复杂自适应系统的网络表示

生物体和生物圈的复杂性

研究人员一直困扰于如何完整定义单个生物体、物种、生态系统、生物进化和生物圈的复杂性，而且这仍然是一个悬而未决的问题。

大多数复杂系统模型通常是根据统计物理学、信息论和非线性动力学的概念来制定的；这些方法并不关注或者说不包括与组织、拓扑属性或代数拓扑有关的复杂性的概念部分，如基因组、交互体和生物有机体的网络连通性这些重要概念。近年来，人们把以信息论、网络拓扑/抽象图论概念为基础的两种互补方法在神经科学和人类认知等领域结合起来。人们普遍认为，组织的复杂程度存在一种应与本体论的现实层次相区别层次结构，现代等级分类的分类方法也承认生物圈的例如:生物领域和生物圈、生物的界、门、纲、目、科、属和种等复杂层次结构。由于生物体具有动态性和组成的可变性、内在的“模糊性”、自生属性、自我繁殖的能力等等，生物体不符合一般系统的“标准”的定义，因此它们在功能和结构上都是“超级复杂”的；因此，在CSB中，生物体只能被定义为一种简单动态系统，“元系统”。这样一个有机体、物种、“生态系统”等等的元系统定义，并不等同于自生系统理论中对系统中的系统的定义。它也不同于K·D·帕尔默在元系统工程中提出的定义，即生物体不同于具有固定输入输出转换函数的机器和自动机，或不同于具有固定相空间的连续动力系统，这与笛卡尔哲学思想相反；因此，尽管“非确定性自动机”和“模糊自动机”也被定义了，但生物体不能仅仅用五组a（状态、启动状态、输入和输出集/字母、转换函数）来定义。然而，棋盘自动机 tessellation automata或元胞自动机 cellular automata 提供了一种直观的、可视化的/计算的视角来洞察较低层次的复杂性，因此已经成为一种越来越流行的离散模型，研究领域包括可计算理论、应用数学、物理、计算机科学、理论生物学/系统生物学、癌症模拟和微观结构建模。利用遗传算法实现元胞自动机是一个桥接棋盘自动机和CSB中的高层次复杂性方法之间差距的新兴领域。

of taxonomic ranks, such as: biological domain and biosphere, biological kingdom, Phylum, biological class, order, family, genus and species. Because of their dynamic and composition variability, intrinsic "fuzziness", autopoietic attributes, ability to self-reproduce, and so on, organisms do not fit into the 'standard' definition of general systems, and they are therefore 'super-complex' in both their function and structure; organisms can be thus be defined in CSB only as 'meta-systems' of simpler dynamic systems^[1]^[2] Such a meta-system definition of organisms, species, 'ecosystems', and so on, is not equivalent to the definition of a system of systems as in Autopoietic Systems Theory,;^[3] it also differs from the definition proposed for example by K.D. Palmer in meta-system engineering,^[4] organisms being quite different from machines and automata with fixed input-output transition functions, or a continuous dynamical system with fixed phase space,^[5] contrary to the Cartesian philosophical thinking; thus, organisms cannot be defined merely in terms of a quintuple A of (states, startup state, input and output sets/alphabet, transition function),^[6] although 'non-deterministic automata', as well as 'fuzzy automata' have also been defined. Tessellation or cellular automata provide however an intuitive, visual/computational insight into the lower levels of complexity, and have therefore become an increasingly popular, discrete model studied in computability theory, applied mathematics, physics, computer science, theoretical biology/systems biology, cancer simulations and microstructure modeling. Evolving cellular automata using genetic algorithms^[7]^[8]^[9] is also an emerging field attempting to bridge the gap between the tessellation automata and the higher level complexity approaches in CSB.

复杂系统生物学的主题

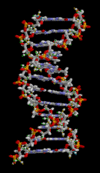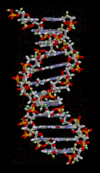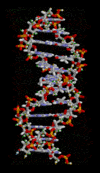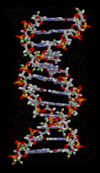
Animated Molecular Model of a DNA double helix

一个DNA双螺旋的动画分子模型

Telomerase structure and function

端粒酶的结构与功能

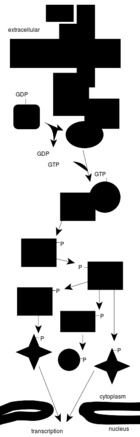
A Complex Signal Transduction Pathway

一个复杂的信号转导途径

以下只是复杂系统生物学所涵盖的部分主题列表:

生物与物种的关系与进化 Organisms and species relations and evolution
物种间的相互作用 Interactions among Species
进化论和种群遗传学 Evolution theories and population genetics
- 群体遗传学模型 Population genetics models
- 表观遗传学 Epigenetics
- 分子进化理论 Molecular evolution theories
量子生物计算学Quantum biocomputation

Quantum genetics^[10]

量子遗传

Relational biology^[11]^[12]^[13]^[14]

关系生物学

Self-reproduction^[15] (also called self-replication in a more general context)

自我繁殖(在更一般的情况下也称为自我复制)

计算基因模型 Computational gene models
- DNA拓扑学 DNA topology
- DNA测序理论 DNA sequencing theory
进化发育生物学 Evolutionary developmental biology
自我生产 Autopoiesis
蛋白质折叠 Protein folding
端粒酶在体内的构象和功能 Telomerase conformations and functions in vivo
表观遗传学 Epigenetics
交互组学 Interactomics^[16]^[17]^[17] < ref name ="hayete2007">

{{cite journal

{引用期刊

|author1=Hayete, B |author2=Gardner, TS |author3=Collins, JJ | year = 2007

1 = Hayete，b | author2 = Gardner，TS | author3 = Collins，JJ | year = 2007

| title = Size matters: network inference tackles the genome scale

| title = 规模问题: 网络推理解决了基因组规模

| journal = Molecular Systems Biology

分子系统生物学

| volume = 3 |issue = 1| pages = 77

3 | issue = 1 | pages = 77

| doi = 10.1038/msb4100118

| pmid = 17299414

17299414

| pmc = 1828748

1828748

}}</ref>

} </ref >

Cell signaling

细胞信号传导

Signal transduction networks

信号转导网络

Complex neural nets

复杂神经网络

Genetic networks

基因网络

Morphogenesis

形态发生

Digital morphogenesis

数字形态发生

Complex adaptive systems

复杂自适应系统

Topological models of morphogenesis

形态形成的拓扑模型

Population dynamics of fisheries

渔业种群动态

Epidemiology

流行病学

Theoretical ecology

理论生态学

Immune system

免疫系统

另请参阅

数学和理论生物学 Mathematical and theoretical biology

抽象关系生物学 Abstract relational biology

复杂 Complexity

复杂系统 Complex system

生物系统 Biological system

系统理论 Systems theory

动力系统 Dynamical system

动力系统理论 Dynamical systems theory

自动机理论 Automata theory

元胞自动机 Cellular automaton

系统生物学Systems biology

人类学中的系统理论 Systems theory in anthropology

自组织 Self-organization

非线性度 Nonlinearity

生成科学 Generative sciences

紧急情况 Emergence

生物圈 Biosphere

脱氧核糖核酸 DNA

量子生物学 Quantum biology

- 量子遗传学 Quantum genetics

- 量子生物化学 Quantum biochemistry

- 量子化学 Quantum chemistry

- 量子分子动力学 Quantum molecular dynamics

蛋白质折叠 Protein folding

交互组学 Interactomics^[16]^[17]

基因组学 Genomics

蛋白质组学 Proteomics

表观遗传学 Epigenetics

数字形态 Digital morphogenesis

复杂自适应系统 Complex adaptive system

多代理系统 Multi-agent systems

认知科学 Cognitive Science

面向模式的建模 Pattern oriented modeling

波动性，不确定性，复杂性和歧义性 Volatility, uncertainty, complexity and ambiguity

蓝色基因 blue Gene

折叠@家 Folding@home

端粒酶 Telomerase

生命是什么 What Is Life?

传记

Charles Darwin

D'Arcy Thompson

William Ross Ashby

Ludwig von Bertalanffy

Ronald Brown

Joseph Fourier

Brian Goodwin

George Karreman

Charles S. Peskin

Nicolas Rashevsky

Robert Rosen

Anatol Rapoport

Rosalind Franklin

Francis Crick

René Thom

Vito Volterra

Norbert Wiener

笔记

↑ 引用错误：无效<ref>标签；未给name属性为springerlink的引用提供文字
↑ Metasystem Transition Theory, Valentin Turchin, Cliff Joslyn, 1993-1997
↑ Reflexive Autopoietic Systems Theory
↑ Meta-system Engineering, Kent D. Palmer, 1996
↑ Hoff, M.A., Roggia, K.G., Menezes, P.B.:(2004). Composition of Transformations: A Framework for Systems with Dynamic Topology. International Journal of Computing Anticipatory System's 14:259–270

↑ John E. Hopcroft, Rajeev Motwani, Jeffrey D. Ullman.2000. Introduction to Automata Theory, Languages, and Computation (2nd Edition)Pearson Education.

↑ The Evolutionary Design of Collective Computation in Cellular Automata, James P. Crutchfeld, Melanie Mitchell, Rajarshi Das (In J. P. Crutchfield and P. K. Schuster (editors), Evolutionary Dynamics|Exploring the Interplay of Selection, Neutrality, Accident, and Function. New York: Oxford University Press, 2002.)
↑ Evolving Cellular Automata with Genetic Algorithms: A Review of Recent Work, Melanie Mitchell, James P. Crutchfeld, Rajarshi Das (In Proceedings of the First International Conference on Evolutionary Computation and Its Applications (EvCA'96). Moscow, Russia: Russian Academy of Sciences, 1996.)
↑ Peak, West; Messinger, Mott; Messinger, SM; Mott, KA (2004). "Evidence for complex, collective dynamics and emergent, distributed computation in plants". Proceedings of the National Academy of Sciences of the USA. 101 (4): 918–922. Bibcode:2004PNAS..101..918P. doi:10.1073/pnas.0307811100. PMC 327117. PMID 14732685.
↑ Rosen, R. 1960. (1960). "A quantum-theoretic approach to genetic problems". Bulletin of Mathematical Biophysics. 22 (3): 227–255. doi:10.1007/BF02478347.
↑ 引用错误：无效<ref>标签；未给name属性为ReferenceA的引用提供文字
↑ Baianu, I. C.: 2006 (2006). "Robert Rosen's Work and Complex Systems Biology". Axiomathes. 16 (1–2): 25–34. doi:10.1007/s10516-005-4204-z.
↑ Rosen, R.: 1958b (1958). "The Representation of Biological Systems from the Standpoint of the Theory of Categories". Bulletin of Mathematical Biophysics. 20 (4): 317–341. doi:10.1007/BF02477890.
↑ PlanetMath
↑ "PlanetMath". PlanetMath. Retrieved 2010-03-17.
↑ ^16.0 ^16.1 {{cite journal {{cite journal {引用期刊 | author = Faith, JJ | author = Faith, JJ 作者 = Faith，JJ | year = 2007 | year = 2007 2007年 | title = Large-Scale Mapping and Validation of Escherichia coli Transcriptional Regulation from a Compendium of Expression Profiles | title = Large-Scale Mapping and Validation of Escherichia coli Transcriptional Regulation from a Compendium of Expression Profiles | title = 大比例绘制和验证表达式概要中的大肠桿菌转录调控 | journal = PLOS Biology | journal = PLOS Biology | journal = PLOS Biology | volume = 5 | issue = 1 | pages = 54–66 | volume = 5 | issue = 1 | pages = 54–66 5 | issue = 1 | pages = 54-66 | doi = 10.1371/journal.pbio.0050008 | doi = 10.1371/journal.pbio.0050008 10.1371/journal.pbio. 0050008 | pmid = 17214507 | pmid = 17214507 17214507 | pmc = 1764438 | pmc = 1764438 1764438 | display-authors = 1 | display-authors = 1 | display-authors = 1 | last2 = Hayete | last2 = Hayete 2 = Hayete | first2 = Boris | first2 = Boris 2 = Boris | last3 = Thaden | last3 = Thaden 3 = Thaden | first3 = Joshua T. | first3 = Joshua T. 3 = Joshua t. | last4 = Mogno | last4 = Mogno 4 = Mogno | first4 = Ilaria | first4 = Ilaria 4 = Ilaria | last5 = Wierzbowski | last5 = Wierzbowski 5 = Wierzbowski | first5 = Jamey | first5 = Jamey 5 = Jamey | last6 = Cottarel | last6 = Cottarel 6 = Cottarel | first6 = Guillaume | first6 = Guillaume 6 = Guillaume | last7 = Kasif | last7 = Kasif 7 = Kasif | first7 = Simon | first7 = Simon 7 = Simon | last8 = Collins | last8 = Collins 8 = Collins | first8 = James J. | first8 = James J. 8 = James j. | last9 = Gardner | last9 = Gardner 9 = Gardner | first9 = Timothy S. | first9 = Timothy S. 9 = Timothy s. }}
↑ ^17.0 ^17.1 ^17.2 }} 引用错误：无效<ref>标签；name属性“Hayete2007”使用不同内容定义了多次

References cited

参考文献引用

Ahmed, E. (2006). "On modeling the immune system as a complex system". Theor. BioSci. 124 (3–4): 413–8. arXiv:0801.0847. Bibcode:2008arXiv0801.0847A. doi:10.1016/j.thbio.2005.07.001. PMID 17046369.

Baianu, I. C., Computer Models and Automata Theory in Biology and Medicine., Monograph, Ch.11 in M. Witten (Editor), Mathematical Models in Medicine, vol. 7., Vol. 7: 1513-1577 (1987),Pergamon Press:New York, (updated by Hsiao Chen Lin in 2004

Bonner, J. T. 1988. The Evolution of Complexity by Means of Natural Selection. Princeton: Princeton University Press.

Donald Snooks, Graeme, "A general theory of complex living systems: Exploring the demand side of dynamics", Complexity, vol. 13, no. 6, July/August 2008.

Drazin, P.G., Nonlinear systems. C.U.P., 1992.

Edelstein-Keshet, L., Mathematical Models in Biology. SIAM, 2004.

Forgacs, G.; S. A. Newman, Biological Physics of the Developing Embryo. C.U.P., 2005.

Israel G (1988). "On the contribution of Volterra and Lotka to the development of modern biomathematics". History and Philosophy of the Life Sciences. 10 (1): 37–49. PMID 3045853.

Israel, G., 2005, "Book on mathematical biology" in Grattan-Guinness, I., ed., Landmark Writings in Western Mathematics. Elsevier: 936-44.

Jordan, D.W.; Smith, P., Nonlinear ordinary differential equations, 2nd ed. O.U.P., 1987.

Kampen, N.G. van. Stochastic Processes in Physics and Chemistry, North Holland., 3rd ed. 2001,

Murray, J.D., Mathematical Biology. Springer-Verlag, 3rd ed. in 2 vols.: Mathematical Biology: I. An Introduction, 2002

; Mathematical Biology: II. Spatial Models and Biomedical Applications, 2003

.

Nicolas Rashevsky. (1938)., Mathematical Biophysics. Chicago: University of Chicago Press.

Preziosi, L., Cancer Modelling and Simulation. Chapman Hall/CRC Press, 2003.

.

Renshaw, E., Modelling biological populations in space and time. C.U.P., 1991.

Rosen, Robert.1991, Life Itself: A Comprehensive Inquiry into the Nature, Origin, and Fabrication of Life, Columbia University Press, published posthumously:

Rosen, Robert .1970. Dynamical system theory in biology. New York, Wiley-Interscience.

Rosen, Robert. 2000, Essays on Life Itself, Columbia University Press.

Rosen, Robert. 2003, "Anticipatory Systems; Philosophical, Mathematical, and Methodolical Foundations", Rosen Enterprises publs.

Rubinow, S.I., Introduction to mathematical biology. John Wiley, 1975.

Scudo FM (March 1971). "Vito Volterra and theoretical ecology". Theoretical Population Biology. 2 (1): 1–23. doi:10.1016/0040-5809(71)90002-5. PMID 4950157.

Segel, L.A., Modeling dynamic phenomena in molecular and cellular biology. C.U.P., 1984.

.

Strogatz, S.H., Nonlinear dynamics and Chaos: Applications to Physics, Biology, Chemistry, and Engineering. Perseus, 2001,

Thompson, D'Arcy W., 1992. On Growth and Form. Dover reprint of 1942, 2nd ed. (1st ed., 1917).

@@ 第12行： / 第12行： @@
-of taxonomic ranks, such as: [[domain (biology)|biological domain]] and biosphere, [[Kingdom (biology)|biological kingdom]], [[Phylum]], [[Class (biology)|biological class]], [[Order (biology)|order]], [[Family (biology)|family]], [[genus]] and [[species]]. Because of their dynamic and composition variability, intrinsic "fuzziness",  autopoietic attributes, ability to self-reproduce, and so on, organisms do not fit into the 'standard' definition of general systems, and they are therefore 'super-complex' in both their function and structure; organisms can be thus be defined in CSB only as '[[meta-system]]s' of simpler dynamic systems<ref name="springerlink" /><ref>[http://pespmc1.vub.ac.be/MST.html Metasystem Transition Theory], [[Valentin Turchin]], [[Cliff Joslyn]], 1993-1997</ref> Such a meta-system definition of organisms, species, 'ecosystems', and so on, is  not equivalent to the definition of a ''system of systems'' as in [[Autopoiesis|Autopoietic System]]s Theory,;<ref>[http://archonic.net Reflexive Autopoietic Systems Theory]</ref> it also differs from the definition proposed for example by K.D. Palmer in meta-system engineering,<ref>[http://archonic.net/incosewg/ppframe.htm Meta-system Engineering], Kent D. Palmer, 1996</ref> organisms being quite different from machines and [[Automata theory|automata]] with fixed input-output transition functions, or a continuous [[dynamical system]] with fixed [[phase space]],<ref>Hoff, M.A., Roggia, K.G., Menezes, P.B.:(2004). Composition of Transformations: A
+of taxonomic ranks, such as: [[domain (biology)|biological domain]] and biosphere, [[Kingdom (biology)|biological kingdom]], [[Phylum]], [[Class (biology)|biological class]], [[Order (biology)|order]], [[Family (biology)|family]], [[genus]] and [[species]]. Because of their dynamic and composition variability, intrinsic "fuzziness",  autopoietic attributes, ability to self-reproduce, and so on, organisms do not fit into the 'standard' definition of general systems, and they are therefore 'super-complex' in both their function and structure; organisms can be thus be defined in CSB only as '[[meta-system]]s' of simpler dynamic systems<ref name="springerlink" /><ref>[http://pespmc1.vub.ac.be/MST.html Metasystem Transition Theory], [[Valentin Turchin]], [[Cliff Joslyn]], 1993-1997</ref> Such a meta-system definition of organisms, species, 'ecosystems', and so on, is  not equivalent to the definition of a ''system of systems'' as in [[Autopoiesis|Autopoietic System]]s Theory,;<ref>[http://archonic.net Reflexive Autopoietic Systems Theory]</ref> it also differs from the definition proposed for example by K.D. Palmer in meta-system engineering,<ref>[http://archonic.net/incosewg/ppframe.htm Meta-system Engineering], Kent D. Palmer, 1996</ref> organisms being quite different from machines and [[Automata theory|automata]] with fixed input-output transition functions, or a continuous [[dynamical system]] with fixed [[phase space]],<ref>Hoff, M.A., Roggia, K.G., Menezes, P.B.:(2004). Composition of Transformations: A Framework for Systems with Dynamic Topology. ''International Journal of Computing Anticipatory System's'' 14:259–270</ref> contrary to the Cartesian philosophical thinking; thus, organisms cannot be defined merely in terms of a quintuple ''A'' of ''(states, startup state, input and output sets/alphabet, transition function)'',<ref>[[John E. Hopcroft]], [[Rajeev Motwani]], [[Jeffrey D. Ullman]].2000. [[Introduction to Automata Theory, Languages, and Computation]] (2nd Edition)Pearson Education. {{ISBN|0-201-44124-1}}</ref> although 'non-deterministic automata', as well as 'fuzzy automata' have also been defined. Tessellation or [[cellular automaton|cellular automata]] provide however an intuitive, visual/computational insight into the lower levels of complexity, and have therefore become an increasingly popular, discrete model studied in computability theory, applied mathematics, physics, computer science, theoretical biology/systems biology, cancer simulations and microstructure modeling. Evolving cellular automata using genetic algorithms<ref>The Evolutionary Design of Collective Computation in Cellular Automata, James P. Crutchfeld, Melanie Mitchell, Rajarshi Das (In J. P. Crutchfield and P. K. Schuster (editors), Evolutionary Dynamics|Exploring the Interplay of Selection, Neutrality, Accident, and Function. New York: Oxford University Press, 2002.)</ref><ref>Evolving Cellular Automata with Genetic Algorithms: A Review of Recent Work, Melanie Mitchell, James P. Crutchfeld, Rajarshi Das (In Proceedings of the First International Conference on Evolutionary Computation and Its Applications (EvCA'96). Moscow, Russia: Russian Academy of Sciences, 1996.)</ref><ref>{{cite journal | doi = 10.1073/pnas.0307811100 | last1 = Peak | first1 = West | last2 = Messinger | first2 = Mott | year = 2004 | title = Evidence for complex, collective dynamics and emergent, distributed computation in plants | journal = Proceedings of the National Academy of Sciences of the USA | volume = 101 | issue = 4| pages = 918–922 |bibcode = 2004PNAS..101..918P | pmid = 14732685 | last3 = Messinger | first3 = SM | last4 = Mott | first4 = KA | pmc = 327117}}</ref> is also an emerging field attempting to bridge the gap between the tessellation automata and the higher level complexity approaches in CSB.
-of taxonomic ranks, such as: biological domain and biosphere, biological kingdom, Phylum, biological class, order, family, genus and species. Because of their dynamic and composition variability, intrinsic "fuzziness",  autopoietic attributes, ability to self-reproduce, and so on, organisms do not fit into the 'standard' definition of general systems, and they are therefore 'super-complex' in both their function and structure; organisms can be thus be defined in CSB only as 'meta-systems' of simpler dynamic systems Such a meta-system definition of organisms, species, 'ecosystems', and so on, is  not equivalent to the definition of a system of systems as in Autopoietic Systems Theory,; it also differs from the definition proposed for example by K.D. Palmer in meta-system engineering, organisms being quite different from machines and automata with fixed input-output transition functions, or a continuous dynamical system with fixed phase space,<ref>Hoff, M.A., Roggia, K.G., Menezes, P.B.:(2004). Composition of Transformations: A
-Framework for Systems with Dynamic Topology. ''International Journal of Computing Anticipatory System's'' 14:259–270</ref> contrary to the Cartesian philosophical thinking; thus, organisms cannot be defined merely in terms of a quintuple ''A'' of ''(states, startup state, input and output sets/alphabet, transition function)'',<ref>[[John E. Hopcroft]], [[Rajeev Motwani]], [[Jeffrey D. Ullman]].2000. [[Introduction to Automata Theory, Languages, and Computation]] (2nd Edition)Pearson Education. {{ISBN|0-201-44124-1}}</ref> although 'non-deterministic automata', as well as 'fuzzy automata' have also been defined. Tessellation or [[cellular automaton|cellular automata]] provide however an intuitive, visual/computational insight into the lower levels of complexity, and have therefore become an increasingly popular, discrete model studied in computability theory, applied mathematics, physics, computer science, theoretical biology/systems biology, cancer simulations and microstructure modeling. Evolving cellular automata using genetic algorithms<ref>The Evolutionary Design of Collective Computation in Cellular Automata, James P. Crutchfeld, Melanie Mitchell, Rajarshi Das (In J. P. Crutchfield and P. K. Schuster (editors), Evolutionary Dynamics|Exploring the Interplay of Selection, Neutrality, Accident, and Function. New York: Oxford University Press, 2002.)</ref><ref>
-Framework for Systems with Dynamic Topology. International Journal of Computing Anticipatory System's 14:259–270</ref> contrary to the Cartesian philosophical thinking; thus, organisms cannot be defined merely in terms of a quintuple A of (states, startup state, input and output sets/alphabet, transition function), although 'non-deterministic automata', as well as 'fuzzy automata' have also been defined. Tessellation or cellular automata provide however an intuitive, visual/computational insight into the lower levels of complexity, and have therefore become an increasingly popular, discrete model studied in computability theory, applied mathematics, physics, computer science, theoretical biology/systems biology, cancer simulations and microstructure modeling. Evolving cellular automata using genetic algorithms<ref>
-Evolving Cellular Automata with Genetic Algorithms: A Review of Recent Work, Melanie Mitchell, James P. Crutchfeld, Rajarshi Das (In Proceedings of the First International Conference on Evolutionary Computation and Its Applications (EvCA'96). Moscow, Russia: Russian Academy of Sciences, 1996.)</ref><ref>{{cite journal | doi = 10.1073/pnas.0307811100 | last1 = Peak | first1 = West | last2 = Messinger | first2 = Mott | year = 2004 | title = Evidence for complex, collective dynamics and emergent, distributed computation in plants | journal = Proceedings of the National Academy of Sciences of the USA | volume = 101 | issue = 4| pages = 918–922 |bibcode = 2004PNAS..101..918P | pmid = 14732685 | last3 = Messinger | first3 = SM | last4 = Mott | first4 = KA | pmc = 327117}}</ref> is also an emerging field attempting to bridge the gap between the tessellation automata and the higher level complexity approaches in CSB.
-Evolving Cellular Automata with Genetic Algorithms: A Review of Recent Work, Melanie Mitchell, James P. Crutchfeld, Rajarshi Das (In Proceedings of the First International Conference on Evolutionary Computation and Its Applications (EvCA'96). Moscow, Russia: Russian Academy of Sciences, 1996.)</ref> is also an emerging field attempting to bridge the gap between the tessellation automata and the higher level complexity approaches in CSB.