“条件互信息”的版本间的差异
小 (Moved page from wikipedia:en:Conditional mutual information (history)) |
|||
| 第1行: | 第1行: | ||
| − | + | 此词条Jie翻译。 | |
{{Information theory}} | {{Information theory}} | ||
| − | |||
| − | |||
[[Image:VennInfo3Var.svg|thumb|256px|right|[[Venn diagram]] of information theoretic measures for three variables <math>x</math>, <math>y</math>, and <math>z</math>, represented by the lower left, lower right, and upper circles, respectively. The conditional mutual informations <math>I(x;z|y)</math>, <math>I(y;z|x)</math> and <math>I(x;y|z)</math> are represented by the yellow, cyan, and magenta regions, respectively.]] | [[Image:VennInfo3Var.svg|thumb|256px|right|[[Venn diagram]] of information theoretic measures for three variables <math>x</math>, <math>y</math>, and <math>z</math>, represented by the lower left, lower right, and upper circles, respectively. The conditional mutual informations <math>I(x;z|y)</math>, <math>I(y;z|x)</math> and <math>I(x;y|z)</math> are represented by the yellow, cyan, and magenta regions, respectively.]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
In [[probability theory]], particularly [[information theory]], the '''conditional mutual information'''<ref name = Wyner1978>{{cite journal|last=Wyner|first=A. D. |title=A definition of conditional mutual information for arbitrary ensembles|url=|journal=Information and Control|year=1978|volume=38|issue=1|pages=51–59|doi=10.1016/s0019-9958(78)90026-8|doi-access=free}}</ref><ref name = Dobrushin1959>{{cite journal|last=Dobrushin|first=R. L. |title=General formulation of Shannon's main theorem in information theory|journal=Uspekhi Mat. Nauk|year=1959|volume=14|pages=3–104}}</ref> is, in its most basic form, the [[expected value]] of the [[mutual information]] of two random variables given the value of a third. | In [[probability theory]], particularly [[information theory]], the '''conditional mutual information'''<ref name = Wyner1978>{{cite journal|last=Wyner|first=A. D. |title=A definition of conditional mutual information for arbitrary ensembles|url=|journal=Information and Control|year=1978|volume=38|issue=1|pages=51–59|doi=10.1016/s0019-9958(78)90026-8|doi-access=free}}</ref><ref name = Dobrushin1959>{{cite journal|last=Dobrushin|first=R. L. |title=General formulation of Shannon's main theorem in information theory|journal=Uspekhi Mat. Nauk|year=1959|volume=14|pages=3–104}}</ref> is, in its most basic form, the [[expected value]] of the [[mutual information]] of two random variables given the value of a third. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Definition== | ==Definition== | ||
| − | |||
For random variables <math>X</math>, <math>Y</math>, and <math>Z</math> with [[Support (mathematics)|support sets]] <math>\mathcal{X}</math>, <math>\mathcal{Y}</math> and <math>\mathcal{Z}</math>, we define the conditional mutual information as | For random variables <math>X</math>, <math>Y</math>, and <math>Z</math> with [[Support (mathematics)|support sets]] <math>\mathcal{X}</math>, <math>\mathcal{Y}</math> and <math>\mathcal{Z}</math>, we define the conditional mutual information as | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{Equation box 1 | {{Equation box 1 | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|indent = | |indent = | ||
| − | |||
| − | |||
| − | |||
|title= | |title= | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|equation = | |equation = | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<math> | <math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
I(X;Y|Z) = \int_\mathcal{Z} D_{\mathrm{KL}}( P_{(X,Y)|Z} \| P_{X|Z} \otimes P_{Y|Z} ) dP_{Z} | I(X;Y|Z) = \int_\mathcal{Z} D_{\mathrm{KL}}( P_{(X,Y)|Z} \| P_{X|Z} \otimes P_{Y|Z} ) dP_{Z} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</math> | </math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|cellpadding= 2 | |cellpadding= 2 | ||
| − | |||
| − | |||
| − | |||
|border | |border | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|border colour = #0073CF | |border colour = #0073CF | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|background colour=#F5FFFA}} | |background colour=#F5FFFA}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
This may be written in terms of the expectation operator: <math>I(X;Y|Z) = \mathbb{E}_Z [D_{\mathrm{KL}}( P_{(X,Y)|Z} \| P_{X|Z} \otimes P_{Y|Z} )]</math>. | This may be written in terms of the expectation operator: <math>I(X;Y|Z) = \mathbb{E}_Z [D_{\mathrm{KL}}( P_{(X,Y)|Z} \| P_{X|Z} \otimes P_{Y|Z} )]</math>. | ||
| − | |||
| − | |||
| − | |||
| − | |||
Thus <math>I(X;Y|Z)</math> is the expected (with respect to <math>Z</math>) [[Kullback–Leibler divergence]] from the conditional joint distribution <math>P_{(X,Y)|Z}</math> to the product of the conditional marginals <math>P_{X|Z}</math> and <math>P_{Y|Z}</math>. Compare with the definition of [[mutual information]]. | Thus <math>I(X;Y|Z)</math> is the expected (with respect to <math>Z</math>) [[Kullback–Leibler divergence]] from the conditional joint distribution <math>P_{(X,Y)|Z}</math> to the product of the conditional marginals <math>P_{X|Z}</math> and <math>P_{Y|Z}</math>. Compare with the definition of [[mutual information]]. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==In terms of pmf's for discrete distributions== | ==In terms of pmf's for discrete distributions== | ||
| − | |||
For discrete random variables <math>X</math>, <math>Y</math>, and <math>Z</math> with [[Support (mathematics)|support sets]] <math>\mathcal{X}</math>, <math>\mathcal{Y}</math> and <math>\mathcal{Z}</math>, the conditional mutual information <math>I(X;Y|Z)</math> is as follows | For discrete random variables <math>X</math>, <math>Y</math>, and <math>Z</math> with [[Support (mathematics)|support sets]] <math>\mathcal{X}</math>, <math>\mathcal{Y}</math> and <math>\mathcal{Z}</math>, the conditional mutual information <math>I(X;Y|Z)</math> is as follows | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
:<math> | :<math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
I(X;Y|Z) = \sum_{z\in \mathcal{Z}} p_Z(z) \sum_{y\in \mathcal{Y}} \sum_{x\in \mathcal{X}} | I(X;Y|Z) = \sum_{z\in \mathcal{Z}} p_Z(z) \sum_{y\in \mathcal{Y}} \sum_{x\in \mathcal{X}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
p_{X,Y|Z}(x,y|z) \log \frac{p_{X,Y|Z}(x,y|z)}{p_{X|Z}(x|z)p_{Y|Z}(y|z)} | p_{X,Y|Z}(x,y|z) \log \frac{p_{X,Y|Z}(x,y|z)}{p_{X|Z}(x|z)p_{Y|Z}(y|z)} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</math> | </math> | ||
| − | |||
| − | |||
| − | |||
where the marginal, joint, and/or conditional [[probability mass function]]s are denoted by <math>p</math> with the appropriate subscript. This can be simplified as | where the marginal, joint, and/or conditional [[probability mass function]]s are denoted by <math>p</math> with the appropriate subscript. This can be simplified as | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{Equation box 1 | {{Equation box 1 | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|indent = | |indent = | ||
| − | |||
| − | |||
| − | |||
|title= | |title= | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|equation = | |equation = | ||
| − | |||
| − | |||
| − | |||
<math> | <math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
I(X;Y|Z) = \sum_{z\in \mathcal{Z}} \sum_{y\in \mathcal{Y}} \sum_{x\in \mathcal{X}} p_{X,Y,Z}(x,y,z) \log \frac{p_Z(z)p_{X,Y,Z}(x,y,z)}{p_{X,Z}(x,z)p_{Y,Z}(y,z)}. | I(X;Y|Z) = \sum_{z\in \mathcal{Z}} \sum_{y\in \mathcal{Y}} \sum_{x\in \mathcal{X}} p_{X,Y,Z}(x,y,z) \log \frac{p_Z(z)p_{X,Y,Z}(x,y,z)}{p_{X,Z}(x,z)p_{Y,Z}(y,z)}. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</math> | </math> | ||
| − | |||
| − | |||
| − | |||
|cellpadding= 6 | |cellpadding= 6 | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|border | |border | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|border colour = #0073CF | |border colour = #0073CF | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|background colour=#F5FFFA}} | |background colour=#F5FFFA}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
==In terms of pdf's for continuous distributions== | ==In terms of pdf's for continuous distributions== | ||
| − | |||
For (absolutely) continuous random variables <math>X</math>, <math>Y</math>, and <math>Z</math> with [[Support (mathematics)|support sets]] <math>\mathcal{X}</math>, <math>\mathcal{Y}</math> and <math>\mathcal{Z}</math>, the conditional mutual information <math>I(X;Y|Z)</math> is as follows | For (absolutely) continuous random variables <math>X</math>, <math>Y</math>, and <math>Z</math> with [[Support (mathematics)|support sets]] <math>\mathcal{X}</math>, <math>\mathcal{Y}</math> and <math>\mathcal{Z}</math>, the conditional mutual information <math>I(X;Y|Z)</math> is as follows | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
:<math> | :<math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
I(X;Y|Z) = \int_{\mathcal{Z}} \bigg( \int_{\mathcal{Y}} \int_{\mathcal{X}} | I(X;Y|Z) = \int_{\mathcal{Z}} \bigg( \int_{\mathcal{Y}} \int_{\mathcal{X}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
\log \left(\frac{p_{X,Y|Z}(x,y|z)}{p_{X|Z}(x|z)p_{Y|Z}(y|z)}\right) p_{X,Y|Z}(x,y|z) dx dy \bigg) p_Z(z) dz | \log \left(\frac{p_{X,Y|Z}(x,y|z)}{p_{X|Z}(x|z)p_{Y|Z}(y|z)}\right) p_{X,Y|Z}(x,y|z) dx dy \bigg) p_Z(z) dz | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</math> | </math> | ||
| − | |||
| − | |||
| − | |||
where the marginal, joint, and/or conditional [[probability density function]]s are denoted by <math>p</math> with the appropriate subscript. This can be simplified as | where the marginal, joint, and/or conditional [[probability density function]]s are denoted by <math>p</math> with the appropriate subscript. This can be simplified as | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{Equation box 1 | {{Equation box 1 | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|indent = | |indent = | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|title= | |title= | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|equation = | |equation = | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<math> | <math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
I(X;Y|Z) = \int_{\mathcal{Z}} \int_{\mathcal{Y}} \int_{\mathcal{X}} \log \left(\frac{p_Z(z)p_{X,Y,Z}(x,y,z)}{p_{X,Z}(x,z)p_{Y,Z}(y,z)}\right) p_{X,Y,Z}(x,y,z) dx dy dz. | I(X;Y|Z) = \int_{\mathcal{Z}} \int_{\mathcal{Y}} \int_{\mathcal{X}} \log \left(\frac{p_Z(z)p_{X,Y,Z}(x,y,z)}{p_{X,Z}(x,z)p_{Y,Z}(y,z)}\right) p_{X,Y,Z}(x,y,z) dx dy dz. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</math> | </math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|cellpadding= 6 | |cellpadding= 6 | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|border | |border | ||
| − | |||
| − | |||
| − | |||
|border colour = #0073CF | |border colour = #0073CF | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|background colour=#F5FFFA}} | |background colour=#F5FFFA}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
==Some identities== | ==Some identities== | ||
| − | |||
Alternatively, we may write in terms of joint and conditional [[Entropy (information theory)|entropies]] as<ref>{{cite book |last1=Cover |first1=Thomas |author-link1=Thomas M. Cover |last2=Thomas |first2=Joy A. |title=Elements of Information Theory |edition=2nd |location=New York |publisher=[[Wiley-Interscience]] |date=2006 |isbn=0-471-24195-4}}</ref> | Alternatively, we may write in terms of joint and conditional [[Entropy (information theory)|entropies]] as<ref>{{cite book |last1=Cover |first1=Thomas |author-link1=Thomas M. Cover |last2=Thomas |first2=Joy A. |title=Elements of Information Theory |edition=2nd |location=New York |publisher=[[Wiley-Interscience]] |date=2006 |isbn=0-471-24195-4}}</ref> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
:<math>I(X;Y|Z) = H(X,Z) + H(Y,Z) - H(X,Y,Z) - H(Z) | :<math>I(X;Y|Z) = H(X,Z) + H(Y,Z) - H(X,Y,Z) - H(Z) | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
= H(X|Z) - H(X|Y,Z) = H(X|Z)+H(Y|Z)-H(X,Y|Z).</math> | = H(X|Z) - H(X|Y,Z) = H(X|Z)+H(Y|Z)-H(X,Y|Z).</math> | ||
| − | |||
| − | |||
| − | |||
This can be rewritten to show its relationship to mutual information | This can be rewritten to show its relationship to mutual information | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
:<math>I(X;Y|Z) = I(X;Y,Z) - I(X;Z)</math> | :<math>I(X;Y|Z) = I(X;Y,Z) - I(X;Z)</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
usually rearranged as '''the chain rule for mutual information''' | usually rearranged as '''the chain rule for mutual information''' | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
:<math>I(X;Y,Z) = I(X;Z) + I(X;Y|Z)</math> | :<math>I(X;Y,Z) = I(X;Z) + I(X;Y|Z)</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Another equivalent form of the above is<ref>[https://math.stackexchange.com/q/1863993 Decomposition on Math.StackExchange]</ref> | Another equivalent form of the above is<ref>[https://math.stackexchange.com/q/1863993 Decomposition on Math.StackExchange]</ref> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
:<math>I(X;Y|Z) = H(Z|X) + H(X) + H(Z|Y) + H(Y) - H(Z|X,Y) - H(X,Y) - H(Z) | :<math>I(X;Y|Z) = H(Z|X) + H(X) + H(Z|Y) + H(Y) - H(Z|X,Y) - H(X,Y) - H(Z) | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
= I(X;Y) + H(Z|X) + H(Z|Y) - H(Z|X,Y) - H(Z)</math> | = I(X;Y) + H(Z|X) + H(Z|Y) - H(Z|X,Y) - H(Z)</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
Like mutual information, conditional mutual information can be expressed as a [[Kullback–Leibler divergence]]: | Like mutual information, conditional mutual information can be expressed as a [[Kullback–Leibler divergence]]: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
:<math> I(X;Y|Z) = D_{\mathrm{KL}}[ p(X,Y,Z) \| p(X|Z)p(Y|Z)p(Z) ]. </math> | :<math> I(X;Y|Z) = D_{\mathrm{KL}}[ p(X,Y,Z) \| p(X|Z)p(Y|Z)p(Z) ]. </math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Or as an expected value of simpler Kullback–Leibler divergences: | Or as an expected value of simpler Kullback–Leibler divergences: | ||
| − | |||
| − | |||
| − | |||
:<math> I(X;Y|Z) = \sum_{z \in \mathcal{Z}} p( Z=z ) D_{\mathrm{KL}}[ p(X,Y|z) \| p(X|z)p(Y|z) ]</math>, | :<math> I(X;Y|Z) = \sum_{z \in \mathcal{Z}} p( Z=z ) D_{\mathrm{KL}}[ p(X,Y|z) \| p(X|z)p(Y|z) ]</math>, | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
:<math> I(X;Y|Z) = \sum_{y \in \mathcal{Y}} p( Y=y ) D_{\mathrm{KL}}[ p(X,Z|y) \| p(X|Z)p(Z|y) ]</math>. | :<math> I(X;Y|Z) = \sum_{y \in \mathcal{Y}} p( Y=y ) D_{\mathrm{KL}}[ p(X,Z|y) \| p(X|Z)p(Z|y) ]</math>. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==More general definition== | ==More general definition== | ||
| − | |||
A more general definition of conditional mutual information, applicable to random variables with continuous or other arbitrary distributions, will depend on the concept of '''[[regular conditional probability]]'''. (See also.<ref>[http://planetmath.org/encyclopedia/ConditionalProbabilityMeasure.html Regular Conditional Probability] on [http://planetmath.org/ PlanetMath]</ref><ref>D. Leao, Jr. et al. ''Regular conditional probability, disintegration of probability and Radon spaces.'' Proyecciones. Vol. 23, No. 1, pp. 15–29, May 2004, Universidad Católica del Norte, Antofagasta, Chile [http://www.scielo.cl/pdf/proy/v23n1/art02.pdf PDF]</ref>) | A more general definition of conditional mutual information, applicable to random variables with continuous or other arbitrary distributions, will depend on the concept of '''[[regular conditional probability]]'''. (See also.<ref>[http://planetmath.org/encyclopedia/ConditionalProbabilityMeasure.html Regular Conditional Probability] on [http://planetmath.org/ PlanetMath]</ref><ref>D. Leao, Jr. et al. ''Regular conditional probability, disintegration of probability and Radon spaces.'' Proyecciones. Vol. 23, No. 1, pp. 15–29, May 2004, Universidad Católica del Norte, Antofagasta, Chile [http://www.scielo.cl/pdf/proy/v23n1/art02.pdf PDF]</ref>) | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Let <math>(\Omega, \mathcal F, \mathfrak P)</math> be a [[probability space]], and let the random variables <math>X</math>, <math>Y</math>, and <math>Z</math> each be defined as a Borel-measurable function from <math>\Omega</math> to some state space endowed with a topological structure. | Let <math>(\Omega, \mathcal F, \mathfrak P)</math> be a [[probability space]], and let the random variables <math>X</math>, <math>Y</math>, and <math>Z</math> each be defined as a Borel-measurable function from <math>\Omega</math> to some state space endowed with a topological structure. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Consider the Borel measure (on the σ-algebra generated by the open sets) in the state space of each random variable defined by assigning each Borel set the <math>\mathfrak P</math>-measure of its preimage in <math>\mathcal F</math>. This is called the [[pushforward measure]] <math>X _* \mathfrak P = \mathfrak P\big(X^{-1}(\cdot)\big).</math> The '''support of a random variable''' is defined to be the [[Support (measure theory)|topological support]] of this measure, i.e. <math>\mathrm{supp}\,X = \mathrm{supp}\,X _* \mathfrak P.</math> | Consider the Borel measure (on the σ-algebra generated by the open sets) in the state space of each random variable defined by assigning each Borel set the <math>\mathfrak P</math>-measure of its preimage in <math>\mathcal F</math>. This is called the [[pushforward measure]] <math>X _* \mathfrak P = \mathfrak P\big(X^{-1}(\cdot)\big).</math> The '''support of a random variable''' is defined to be the [[Support (measure theory)|topological support]] of this measure, i.e. <math>\mathrm{supp}\,X = \mathrm{supp}\,X _* \mathfrak P.</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Now we can formally define the [[conditional probability distribution|conditional probability measure]] given the value of one (or, via the [[product topology]], more) of the random variables. Let <math>M</math> be a measurable subset of <math>\Omega,</math> (i.e. <math>M \in \mathcal F,</math>) and let <math>x \in \mathrm{supp}\,X.</math> Then, using the [[disintegration theorem]]: | Now we can formally define the [[conditional probability distribution|conditional probability measure]] given the value of one (or, via the [[product topology]], more) of the random variables. Let <math>M</math> be a measurable subset of <math>\Omega,</math> (i.e. <math>M \in \mathcal F,</math>) and let <math>x \in \mathrm{supp}\,X.</math> Then, using the [[disintegration theorem]]: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
:<math>\mathfrak P(M | X=x) = \lim_{U \ni x} | :<math>\mathfrak P(M | X=x) = \lim_{U \ni x} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
\frac {\mathfrak P(M \cap \{X \in U\})} | \frac {\mathfrak P(M \cap \{X \in U\})} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{\mathfrak P(\{X \in U\})} | {\mathfrak P(\{X \in U\})} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
\qquad \textrm{and} \qquad \mathfrak P(M|X) = \int_M d\mathfrak P\big(\omega|X=X(\omega)\big),</math> | \qquad \textrm{and} \qquad \mathfrak P(M|X) = \int_M d\mathfrak P\big(\omega|X=X(\omega)\big),</math> | ||
| − | |||
| − | |||
| − | |||
where the limit is taken over the open neighborhoods <math>U</math> of <math>x</math>, as they are allowed to become arbitrarily smaller with respect to [[Subset|set inclusion]]. | where the limit is taken over the open neighborhoods <math>U</math> of <math>x</math>, as they are allowed to become arbitrarily smaller with respect to [[Subset|set inclusion]]. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Finally we can define the conditional mutual information via [[Lebesgue integration]]: | Finally we can define the conditional mutual information via [[Lebesgue integration]]: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
:<math>I(X;Y|Z) = \int_\Omega \log | :<math>I(X;Y|Z) = \int_\Omega \log | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
\Bigl( | \Bigl( | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
\frac {d \mathfrak P(\omega|X,Z)\, d\mathfrak P(\omega|Y,Z)} | \frac {d \mathfrak P(\omega|X,Z)\, d\mathfrak P(\omega|Y,Z)} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{d \mathfrak P(\omega|Z)\, d\mathfrak P(\omega|X,Y,Z)} | {d \mathfrak P(\omega|Z)\, d\mathfrak P(\omega|X,Y,Z)} | ||
| − | |||
| − | |||
| − | |||
\Bigr) | \Bigr) | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
d \mathfrak P(\omega), | d \mathfrak P(\omega), | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</math> | </math> | ||
| − | |||
| − | |||
| − | |||
where the integrand is the logarithm of a [[Radon–Nikodym derivative]] involving some of the conditional probability measures we have just defined. | where the integrand is the logarithm of a [[Radon–Nikodym derivative]] involving some of the conditional probability measures we have just defined. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Note on notation== | ==Note on notation== | ||
| − | |||
In an expression such as <math>I(A;B|C),</math> <math>A,</math> <math>B,</math> and <math>C</math> need not necessarily be restricted to representing individual random variables, but could also represent the joint distribution of any collection of random variables defined on the same [[probability space]]. As is common in [[probability theory]], we may use the comma to denote such a joint distribution, e.g. <math>I(A_0,A_1;B_1,B_2,B_3|C_0,C_1).</math> Hence the use of the semicolon (or occasionally a colon or even a wedge <math>\wedge</math>) to separate the principal arguments of the mutual information symbol. (No such distinction is necessary in the symbol for [[joint entropy]], since the joint entropy of any number of random variables is the same as the entropy of their joint distribution.) | In an expression such as <math>I(A;B|C),</math> <math>A,</math> <math>B,</math> and <math>C</math> need not necessarily be restricted to representing individual random variables, but could also represent the joint distribution of any collection of random variables defined on the same [[probability space]]. As is common in [[probability theory]], we may use the comma to denote such a joint distribution, e.g. <math>I(A_0,A_1;B_1,B_2,B_3|C_0,C_1).</math> Hence the use of the semicolon (or occasionally a colon or even a wedge <math>\wedge</math>) to separate the principal arguments of the mutual information symbol. (No such distinction is necessary in the symbol for [[joint entropy]], since the joint entropy of any number of random variables is the same as the entropy of their joint distribution.) | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Properties == | == Properties == | ||
| − | |||
===Nonnegativity=== | ===Nonnegativity=== | ||
| − | |||
| − | |||
| − | |||
It is always true that | It is always true that | ||
| − | |||
| − | |||
| − | |||
:<math>I(X;Y|Z) \ge 0</math>, | :<math>I(X;Y|Z) \ge 0</math>, | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
for discrete, jointly distributed random variables <math>X</math>, <math>Y</math> and <math>Z</math>. This result has been used as a basic building block for proving other [[inequalities in information theory]], in particular, those known as Shannon-type inequalities. Conditional mutual information is also non-negative for continuous random variables under certain regularity conditions.<ref>{{cite book |last1=Polyanskiy |first1=Yury |last2=Wu |first2=Yihong |title=Lecture notes on information theory |date=2017 |page=30 |url=http://people.lids.mit.edu/yp/homepage/data/itlectures_v5.pdf}}</ref> | for discrete, jointly distributed random variables <math>X</math>, <math>Y</math> and <math>Z</math>. This result has been used as a basic building block for proving other [[inequalities in information theory]], in particular, those known as Shannon-type inequalities. Conditional mutual information is also non-negative for continuous random variables under certain regularity conditions.<ref>{{cite book |last1=Polyanskiy |first1=Yury |last2=Wu |first2=Yihong |title=Lecture notes on information theory |date=2017 |page=30 |url=http://people.lids.mit.edu/yp/homepage/data/itlectures_v5.pdf}}</ref> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===Interaction information=== | ===Interaction information=== | ||
| − | |||
Conditioning on a third random variable may either increase or decrease the mutual information: that is, the difference <math>I(X;Y) - I(X;Y|Z)</math>, called the [[interaction information]], may be positive, negative, or zero. This is the case even when random variables are pairwise independent. Such is the case when: <math display="block">X \sim \mathrm{Bernoulli}(0.5), Z \sim \mathrm{Bernoulli}(0.5), \quad Y=\left\{\begin{array}{ll} X & \text{if }Z=0\\ 1-X & \text{if }Z=1 \end{array}\right.</math>in which case <math>X</math>, <math>Y</math> and <math>Z</math> are pairwise independent and in particular <math>I(X;Y)=0</math>, but <math>I(X;Y|Z)=1.</math> | Conditioning on a third random variable may either increase or decrease the mutual information: that is, the difference <math>I(X;Y) - I(X;Y|Z)</math>, called the [[interaction information]], may be positive, negative, or zero. This is the case even when random variables are pairwise independent. Such is the case when: <math display="block">X \sim \mathrm{Bernoulli}(0.5), Z \sim \mathrm{Bernoulli}(0.5), \quad Y=\left\{\begin{array}{ll} X & \text{if }Z=0\\ 1-X & \text{if }Z=1 \end{array}\right.</math>in which case <math>X</math>, <math>Y</math> and <math>Z</math> are pairwise independent and in particular <math>I(X;Y)=0</math>, but <math>I(X;Y|Z)=1.</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===Chain rule for mutual information=== | ===Chain rule for mutual information=== | ||
| − | |||
:<math>I(X;Y,Z) = I(X;Z) + I(X;Y|Z)</math> | :<math>I(X;Y,Z) = I(X;Z) + I(X;Y|Z)</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Multivariate mutual information== | ==Multivariate mutual information== | ||
| − | |||
{{main|Multivariate mutual information}} | {{main|Multivariate mutual information}} | ||
| − | |||
The conditional mutual information can be used to inductively define a '''multivariate mutual information''' in a set- or [[Information theory and measure theory|measure-theoretic sense]] in the context of '''[[information diagram]]s'''. In this sense we define the multivariate mutual information as follows: | The conditional mutual information can be used to inductively define a '''multivariate mutual information''' in a set- or [[Information theory and measure theory|measure-theoretic sense]] in the context of '''[[information diagram]]s'''. In this sense we define the multivariate mutual information as follows: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
:<math>I(X_1;\ldots;X_{n+1}) = I(X_1;\ldots;X_n) - I(X_1;\ldots;X_n|X_{n+1}),</math> | :<math>I(X_1;\ldots;X_{n+1}) = I(X_1;\ldots;X_n) - I(X_1;\ldots;X_n|X_{n+1}),</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
where | where | ||
| − | |||
| − | |||
| − | |||
:<math>I(X_1;\ldots;X_n|X_{n+1}) = \mathbb{E}_{X_{n+1}} [D_{\mathrm{KL}}( P_{(X_1,\ldots,X_n)|X_{n+1}} \| P_{X_1|X_{n+1}} \otimes\cdots\otimes P_{X_n|X_{n+1}} )].</math> | :<math>I(X_1;\ldots;X_n|X_{n+1}) = \mathbb{E}_{X_{n+1}} [D_{\mathrm{KL}}( P_{(X_1,\ldots,X_n)|X_{n+1}} \| P_{X_1|X_{n+1}} \otimes\cdots\otimes P_{X_n|X_{n+1}} )].</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
This definition is identical to that of [[interaction information]] except for a change in sign in the case of an odd number of random variables. A complication is that this multivariate mutual information (as well as the interaction information) can be positive, negative, or zero, which makes this quantity difficult to interpret intuitively. In fact, for <math>n</math> random variables, there are <math>2^n-1</math> degrees of freedom for how they might be correlated in an information-theoretic sense, corresponding to each non-empty subset of these variables. These degrees of freedom are bounded by various Shannon- and non-Shannon-type [[inequalities in information theory]]. | This definition is identical to that of [[interaction information]] except for a change in sign in the case of an odd number of random variables. A complication is that this multivariate mutual information (as well as the interaction information) can be positive, negative, or zero, which makes this quantity difficult to interpret intuitively. In fact, for <math>n</math> random variables, there are <math>2^n-1</math> degrees of freedom for how they might be correlated in an information-theoretic sense, corresponding to each non-empty subset of these variables. These degrees of freedom are bounded by various Shannon- and non-Shannon-type [[inequalities in information theory]]. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==References== | ==References== | ||
| − | |||
<references/> | <references/> | ||
| − | |||
| − | |||
[[Category:Information theory]] | [[Category:Information theory]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
[[Category:Entropy and information]] | [[Category:Entropy and information]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
2020年11月3日 (二) 17:43的版本
此词条Jie翻译。
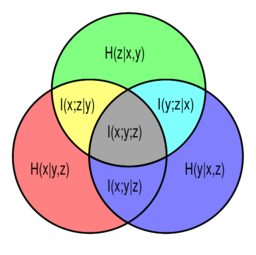
In probability theory, particularly information theory, the conditional mutual information[1][2] is, in its most basic form, the expected value of the mutual information of two random variables given the value of a third.
Definition
For random variables [math]\displaystyle{ X }[/math], [math]\displaystyle{ Y }[/math], and [math]\displaystyle{ Z }[/math] with support sets [math]\displaystyle{ \mathcal{X} }[/math], [math]\displaystyle{ \mathcal{Y} }[/math] and [math]\displaystyle{ \mathcal{Z} }[/math], we define the conditional mutual information as
[math]\displaystyle{ I(X;Y|Z) = \int_\mathcal{Z} D_{\mathrm{KL}}( P_{(X,Y)|Z} \| P_{X|Z} \otimes P_{Y|Z} ) dP_{Z} }[/math]
This may be written in terms of the expectation operator: [math]\displaystyle{ I(X;Y|Z) = \mathbb{E}_Z [D_{\mathrm{KL}}( P_{(X,Y)|Z} \| P_{X|Z} \otimes P_{Y|Z} )] }[/math].
Thus [math]\displaystyle{ I(X;Y|Z) }[/math] is the expected (with respect to [math]\displaystyle{ Z }[/math]) Kullback–Leibler divergence from the conditional joint distribution [math]\displaystyle{ P_{(X,Y)|Z} }[/math] to the product of the conditional marginals [math]\displaystyle{ P_{X|Z} }[/math] and [math]\displaystyle{ P_{Y|Z} }[/math]. Compare with the definition of mutual information.
In terms of pmf's for discrete distributions
For discrete random variables [math]\displaystyle{ X }[/math], [math]\displaystyle{ Y }[/math], and [math]\displaystyle{ Z }[/math] with support sets [math]\displaystyle{ \mathcal{X} }[/math], [math]\displaystyle{ \mathcal{Y} }[/math] and [math]\displaystyle{ \mathcal{Z} }[/math], the conditional mutual information [math]\displaystyle{ I(X;Y|Z) }[/math] is as follows
- [math]\displaystyle{ I(X;Y|Z) = \sum_{z\in \mathcal{Z}} p_Z(z) \sum_{y\in \mathcal{Y}} \sum_{x\in \mathcal{X}} p_{X,Y|Z}(x,y|z) \log \frac{p_{X,Y|Z}(x,y|z)}{p_{X|Z}(x|z)p_{Y|Z}(y|z)} }[/math]
where the marginal, joint, and/or conditional probability mass functions are denoted by [math]\displaystyle{ p }[/math] with the appropriate subscript. This can be simplified as
[math]\displaystyle{ I(X;Y|Z) = \sum_{z\in \mathcal{Z}} \sum_{y\in \mathcal{Y}} \sum_{x\in \mathcal{X}} p_{X,Y,Z}(x,y,z) \log \frac{p_Z(z)p_{X,Y,Z}(x,y,z)}{p_{X,Z}(x,z)p_{Y,Z}(y,z)}. }[/math]
In terms of pdf's for continuous distributions
For (absolutely) continuous random variables [math]\displaystyle{ X }[/math], [math]\displaystyle{ Y }[/math], and [math]\displaystyle{ Z }[/math] with support sets [math]\displaystyle{ \mathcal{X} }[/math], [math]\displaystyle{ \mathcal{Y} }[/math] and [math]\displaystyle{ \mathcal{Z} }[/math], the conditional mutual information [math]\displaystyle{ I(X;Y|Z) }[/math] is as follows
- [math]\displaystyle{ I(X;Y|Z) = \int_{\mathcal{Z}} \bigg( \int_{\mathcal{Y}} \int_{\mathcal{X}} \log \left(\frac{p_{X,Y|Z}(x,y|z)}{p_{X|Z}(x|z)p_{Y|Z}(y|z)}\right) p_{X,Y|Z}(x,y|z) dx dy \bigg) p_Z(z) dz }[/math]
where the marginal, joint, and/or conditional probability density functions are denoted by [math]\displaystyle{ p }[/math] with the appropriate subscript. This can be simplified as
[math]\displaystyle{ I(X;Y|Z) = \int_{\mathcal{Z}} \int_{\mathcal{Y}} \int_{\mathcal{X}} \log \left(\frac{p_Z(z)p_{X,Y,Z}(x,y,z)}{p_{X,Z}(x,z)p_{Y,Z}(y,z)}\right) p_{X,Y,Z}(x,y,z) dx dy dz. }[/math]
Some identities
Alternatively, we may write in terms of joint and conditional entropies as[3]
- [math]\displaystyle{ I(X;Y|Z) = H(X,Z) + H(Y,Z) - H(X,Y,Z) - H(Z) = H(X|Z) - H(X|Y,Z) = H(X|Z)+H(Y|Z)-H(X,Y|Z). }[/math]
This can be rewritten to show its relationship to mutual information
- [math]\displaystyle{ I(X;Y|Z) = I(X;Y,Z) - I(X;Z) }[/math]
usually rearranged as the chain rule for mutual information
- [math]\displaystyle{ I(X;Y,Z) = I(X;Z) + I(X;Y|Z) }[/math]
Another equivalent form of the above is[4]
- [math]\displaystyle{ I(X;Y|Z) = H(Z|X) + H(X) + H(Z|Y) + H(Y) - H(Z|X,Y) - H(X,Y) - H(Z) = I(X;Y) + H(Z|X) + H(Z|Y) - H(Z|X,Y) - H(Z) }[/math]
Like mutual information, conditional mutual information can be expressed as a Kullback–Leibler divergence:
- [math]\displaystyle{ I(X;Y|Z) = D_{\mathrm{KL}}[ p(X,Y,Z) \| p(X|Z)p(Y|Z)p(Z) ]. }[/math]
Or as an expected value of simpler Kullback–Leibler divergences:
- [math]\displaystyle{ I(X;Y|Z) = \sum_{z \in \mathcal{Z}} p( Z=z ) D_{\mathrm{KL}}[ p(X,Y|z) \| p(X|z)p(Y|z) ] }[/math],
- [math]\displaystyle{ I(X;Y|Z) = \sum_{y \in \mathcal{Y}} p( Y=y ) D_{\mathrm{KL}}[ p(X,Z|y) \| p(X|Z)p(Z|y) ] }[/math].
More general definition
A more general definition of conditional mutual information, applicable to random variables with continuous or other arbitrary distributions, will depend on the concept of regular conditional probability. (See also.[5][6])
Let [math]\displaystyle{ (\Omega, \mathcal F, \mathfrak P) }[/math] be a probability space, and let the random variables [math]\displaystyle{ X }[/math], [math]\displaystyle{ Y }[/math], and [math]\displaystyle{ Z }[/math] each be defined as a Borel-measurable function from [math]\displaystyle{ \Omega }[/math] to some state space endowed with a topological structure.
Consider the Borel measure (on the σ-algebra generated by the open sets) in the state space of each random variable defined by assigning each Borel set the [math]\displaystyle{ \mathfrak P }[/math]-measure of its preimage in [math]\displaystyle{ \mathcal F }[/math]. This is called the pushforward measure [math]\displaystyle{ X _* \mathfrak P = \mathfrak P\big(X^{-1}(\cdot)\big). }[/math] The support of a random variable is defined to be the topological support of this measure, i.e. [math]\displaystyle{ \mathrm{supp}\,X = \mathrm{supp}\,X _* \mathfrak P. }[/math]
Now we can formally define the conditional probability measure given the value of one (or, via the product topology, more) of the random variables. Let [math]\displaystyle{ M }[/math] be a measurable subset of [math]\displaystyle{ \Omega, }[/math] (i.e. [math]\displaystyle{ M \in \mathcal F, }[/math]) and let [math]\displaystyle{ x \in \mathrm{supp}\,X. }[/math] Then, using the disintegration theorem:
- [math]\displaystyle{ \mathfrak P(M | X=x) = \lim_{U \ni x} \frac {\mathfrak P(M \cap \{X \in U\})} {\mathfrak P(\{X \in U\})} \qquad \textrm{and} \qquad \mathfrak P(M|X) = \int_M d\mathfrak P\big(\omega|X=X(\omega)\big), }[/math]
where the limit is taken over the open neighborhoods [math]\displaystyle{ U }[/math] of [math]\displaystyle{ x }[/math], as they are allowed to become arbitrarily smaller with respect to set inclusion.
Finally we can define the conditional mutual information via Lebesgue integration:
- [math]\displaystyle{ I(X;Y|Z) = \int_\Omega \log \Bigl( \frac {d \mathfrak P(\omega|X,Z)\, d\mathfrak P(\omega|Y,Z)} {d \mathfrak P(\omega|Z)\, d\mathfrak P(\omega|X,Y,Z)} \Bigr) d \mathfrak P(\omega), }[/math]
where the integrand is the logarithm of a Radon–Nikodym derivative involving some of the conditional probability measures we have just defined.
Note on notation
In an expression such as [math]\displaystyle{ I(A;B|C), }[/math] [math]\displaystyle{ A, }[/math] [math]\displaystyle{ B, }[/math] and [math]\displaystyle{ C }[/math] need not necessarily be restricted to representing individual random variables, but could also represent the joint distribution of any collection of random variables defined on the same probability space. As is common in probability theory, we may use the comma to denote such a joint distribution, e.g. [math]\displaystyle{ I(A_0,A_1;B_1,B_2,B_3|C_0,C_1). }[/math] Hence the use of the semicolon (or occasionally a colon or even a wedge [math]\displaystyle{ \wedge }[/math]) to separate the principal arguments of the mutual information symbol. (No such distinction is necessary in the symbol for joint entropy, since the joint entropy of any number of random variables is the same as the entropy of their joint distribution.)
Properties
Nonnegativity
It is always true that
- [math]\displaystyle{ I(X;Y|Z) \ge 0 }[/math],
for discrete, jointly distributed random variables [math]\displaystyle{ X }[/math], [math]\displaystyle{ Y }[/math] and [math]\displaystyle{ Z }[/math]. This result has been used as a basic building block for proving other inequalities in information theory, in particular, those known as Shannon-type inequalities. Conditional mutual information is also non-negative for continuous random variables under certain regularity conditions.[7]
Interaction information
Conditioning on a third random variable may either increase or decrease the mutual information: that is, the difference [math]\displaystyle{ I(X;Y) - I(X;Y|Z) }[/math], called the interaction information, may be positive, negative, or zero. This is the case even when random variables are pairwise independent. Such is the case when: [math]\displaystyle{ X \sim \mathrm{Bernoulli}(0.5), Z \sim \mathrm{Bernoulli}(0.5), \quad Y=\left\{\begin{array}{ll} X & \text{if }Z=0\\ 1-X & \text{if }Z=1 \end{array}\right. }[/math]in which case [math]\displaystyle{ X }[/math], [math]\displaystyle{ Y }[/math] and [math]\displaystyle{ Z }[/math] are pairwise independent and in particular [math]\displaystyle{ I(X;Y)=0 }[/math], but [math]\displaystyle{ I(X;Y|Z)=1. }[/math]
Chain rule for mutual information
- [math]\displaystyle{ I(X;Y,Z) = I(X;Z) + I(X;Y|Z) }[/math]
Multivariate mutual information
The conditional mutual information can be used to inductively define a multivariate mutual information in a set- or measure-theoretic sense in the context of information diagrams. In this sense we define the multivariate mutual information as follows:
- [math]\displaystyle{ I(X_1;\ldots;X_{n+1}) = I(X_1;\ldots;X_n) - I(X_1;\ldots;X_n|X_{n+1}), }[/math]
where
- [math]\displaystyle{ I(X_1;\ldots;X_n|X_{n+1}) = \mathbb{E}_{X_{n+1}} [D_{\mathrm{KL}}( P_{(X_1,\ldots,X_n)|X_{n+1}} \| P_{X_1|X_{n+1}} \otimes\cdots\otimes P_{X_n|X_{n+1}} )]. }[/math]
This definition is identical to that of interaction information except for a change in sign in the case of an odd number of random variables. A complication is that this multivariate mutual information (as well as the interaction information) can be positive, negative, or zero, which makes this quantity difficult to interpret intuitively. In fact, for [math]\displaystyle{ n }[/math] random variables, there are [math]\displaystyle{ 2^n-1 }[/math] degrees of freedom for how they might be correlated in an information-theoretic sense, corresponding to each non-empty subset of these variables. These degrees of freedom are bounded by various Shannon- and non-Shannon-type inequalities in information theory.
References
- ↑ Wyner, A. D. (1978). "A definition of conditional mutual information for arbitrary ensembles". Information and Control. 38 (1): 51–59. doi:10.1016/s0019-9958(78)90026-8.
- ↑ Dobrushin, R. L. (1959). "General formulation of Shannon's main theorem in information theory". Uspekhi Mat. Nauk. 14: 3–104.
- ↑ Cover, Thomas; Thomas, Joy A. (2006). Elements of Information Theory (2nd ed.). New York: Wiley-Interscience. ISBN 0-471-24195-4.
- ↑ Decomposition on Math.StackExchange
- ↑ Regular Conditional Probability on PlanetMath
- ↑ D. Leao, Jr. et al. Regular conditional probability, disintegration of probability and Radon spaces. Proyecciones. Vol. 23, No. 1, pp. 15–29, May 2004, Universidad Católica del Norte, Antofagasta, Chile PDF
- ↑ Polyanskiy, Yury; Wu, Yihong (2017). Lecture notes on information theory. p. 30. http://people.lids.mit.edu/yp/homepage/data/itlectures_v5.pdf.