“复杂系统生物学”的版本间的差异
| 第10行: | 第10行: | ||
[[File:Seawifs_global_biosphere.jpg|thumb|right]] | [[File:Seawifs_global_biosphere.jpg|thumb|right]] | ||
| − | 大多数复杂系统模型通常是根据统计物理学、信息论和非线性动力学的概念来制定的;这些方法并不关注或者说不包括与组织、拓扑属性或代数拓扑有关的复杂性的概念部分,如基因组、交互体和生物有机体的网络连通性这些重要概念<ref name="Rosen" /><ref>^ Heylighen, Francis (2008). "Complexity and Self-Organization". In Bates, Marcia J.; Maack, Mary Niles. Encyclopedia of Library and Information Sciences. CRC.</ref><ref>"abstract relational biology (ARB)". PlanetPhysics. Retrieved 2010-03-17.</ref>。近年来,人们把以信息论、网络拓扑/抽象图论概念为基础的两种互补方法在神经科学和人类认知等领域结合起来<ref name="springerlink" /><ref>http://hdl.handle.net/10101/npre.2011.6115.1 Wallace, Rodrick. When Spandrels Become Arches: Neural crosstalk and the evolution of consciousness. Available from Nature Precedings (2011)</ref>。人们普遍认为,组织的复杂程度存在一种应与本体论的现实层次相区别层次结构<ref name="springerlink" /><ref>{{cite journal | author = Poli R | year = 2001a | title = The Basic Problem of the Theory of Levels of Reality | url = | journal = Axiomathes | volume = 12 | issue = 3–4| pages = 261–283 | doi = 10.1023/A:1015845217681 | s2cid = 55743057 }}</ref><ref>{{cite journal | author = Poli R | year = 1998 | title = Levels | url = | journal = Axiomathes | volume = 9 | issue = 1–2| pages = 197–211 | doi=10.1007/bf02681712| pmid = 8053082 }}</ref>,现代等级分类的分类方法也承认生物圈的例如:生物领域和生物圈、生物的界、门、纲、目、科、属和种等复杂层次结构。由于生物体具有动态性和组成的可变性、内在的“模糊性”、自生属性、自我繁殖的能力等等,生物体不符合一般系统的“标准”的定义,因此它们在功能和结构上都是“超级复杂”的;因此,在CSB中,生物体只能被定义为一种简单动态系统,“元系统”<ref name="springerlink" /><ref>[http://pespmc1.vub.ac.be/MST.html Metasystem Transition Theory], [[Valentin Turchin]], [[Cliff Joslyn]], 1993-1997 | + | 大多数复杂系统模型通常是根据统计物理学、信息论和非线性动力学的概念来制定的;这些方法并不关注或者说不包括与组织、拓扑属性或代数拓扑有关的复杂性的概念部分,如基因组、交互体和生物有机体的网络连通性这些重要概念<ref name="Rosen" /><ref>^ Heylighen, Francis (2008). "Complexity and Self-Organization". In Bates, Marcia J.; Maack, Mary Niles. Encyclopedia of Library and Information Sciences. CRC.</ref><ref>"abstract relational biology (ARB)". PlanetPhysics. Retrieved 2010-03-17.</ref>。近年来,人们把以信息论、网络拓扑/抽象图论概念为基础的两种互补方法在神经科学和人类认知等领域结合起来<ref name="springerlink" /><ref>http://hdl.handle.net/10101/npre.2011.6115.1 Wallace, Rodrick. When Spandrels Become Arches: Neural crosstalk and the evolution of consciousness. Available from Nature Precedings (2011)</ref>。人们普遍认为,组织的复杂程度存在一种应与本体论的现实层次相区别层次结构<ref name="springerlink" /><ref>{{cite journal | author = Poli R | year = 2001a | title = The Basic Problem of the Theory of Levels of Reality | url = | journal = Axiomathes | volume = 12 | issue = 3–4| pages = 261–283 | doi = 10.1023/A:1015845217681 | s2cid = 55743057 }}</ref><ref>{{cite journal | author = Poli R | year = 1998 | title = Levels | url = | journal = Axiomathes | volume = 9 | issue = 1–2| pages = 197–211 | doi=10.1007/bf02681712| pmid = 8053082 }}</ref>,现代等级分类的分类方法也承认生物圈的例如:生物领域和生物圈、生物的界、门、纲、目、科、属和种等复杂层次结构。由于生物体具有动态性和组成的可变性、内在的“模糊性”、自生属性、自我繁殖的能力等等,生物体不符合一般系统的“标准”的定义,因此它们在功能和结构上都是“超级复杂”的;因此,在CSB中,生物体只能被定义为一种简单动态系统,“元系统”<ref name="springerlink" /><ref>[http://pespmc1.vub.ac.be/MST.html Metasystem Transition Theory], [[Valentin Turchin]], [[Cliff Joslyn]], 1993-1997</ref>。这样一个有机体、物种、“生态系统”等等的元系统定义 ,如自生系统理论中所述的系统的系统<ref>[http://archonic.net Reflexive Autopoietic Systems Theory]</ref>。它也不同于K·D·帕尔默在元系统工程中提出的定义<ref>[http://archonic.net/incosewg/ppframe.htm Meta-system Engineering], Kent D. Palmer, 1996</ref>,即生物体不同于具有固定输入输出转换函数的机器和自动机,或不同于具有固定相空间的连续动力系统<ref>Hoff, M.A., Roggia, K.G., Menezes, P.B.:(2004). Composition of Transformations: A Framework for Systems with Dynamic Topology. ''International Journal of Computing Anticipatory System's'' 14:259–270</ref>,这与笛卡尔哲学思想相反;因此,尽管“非确定性自动机”和“模糊自动机”也被定义了,但生物体不能仅仅用五组a(状态、启动状态、输入和输出集/字母、转换函数)来定义<ref>Hoff, M.A., Roggia, K.G., Menezes, P.B.:(2004). Composition of Transformations: A Framework for Systems with Dynamic Topology. ''International Journal of Computing Anticipatory System's'' 14:259–270</ref>。然而,棋盘自动机 tessellation automata或元胞自动机 cellular automata 提供了一种直观的、可视化的/计算的视角来洞察较低层次的复杂性,因此已经成为一种越来越流行的离散模型,研究领域包括可计算理论、应用数学、物理、计算机科学、理论生物学/系统生物学、癌症模拟和微观结构建模。利用遗传算法<ref>The Evolutionary Design of Collective Computation in Cellular Automata, James P. Crutchfeld, Melanie Mitchell, Rajarshi Das (In J. P. Crutchfield and P. K. Schuster (editors), Evolutionary Dynamics|Exploring the Interplay of Selection, Neutrality, Accident, and Function. New York: Oxford University Press, 2002.)</ref><ref>Evolving Cellular Automata with Genetic Algorithms: A Review of Recent Work, Melanie Mitchell, James P. Crutchfeld, Rajarshi Das (In Proceedings of the First International Conference on Evolutionary Computation and Its Applications (EvCA'96). Moscow, Russia: Russian Academy of Sciences, 1996.)</ref><ref>{{cite journal | doi = 10.1073/pnas.0307811100 | last1 = Peak | first1 = West | last2 = Messinger | first2 = Mott | year = 2004 | title = Evidence for complex, collective dynamics and emergent, distributed computation in plants | journal = Proceedings of the National Academy of Sciences of the USA | volume = 101 | issue = 4| pages = 918–922 |bibcode = 2004PNAS..101..918P | pmid = 14732685 | last3 = Messinger | first3 = SM | last4 = Mott | first4 = KA | pmc = 327117}}</ref> 实现元胞自动机是一个桥接棋盘自动机和CSB中的高层次复杂性方法之间差距的新兴领域。 |
==复杂系统生物学的主题== | ==复杂系统生物学的主题== | ||
2020年11月4日 (三) 16:56的版本
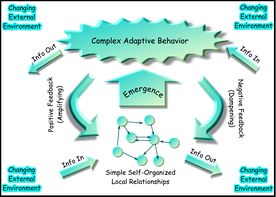
复杂系统生物学 Complex system biology (CSB)是数学和理论生物学的一个分支或子领域,研究生物有机体结构和功能的复杂性,以及生物和物种的出现与进化,重点研究生物网络及其内部的复杂相互作用[1],以及生命所必须的基本关系与关系模式[2][3][4][5][6] CSB is thus a field of theoretical sciences aimed at discovering and modeling the relational patterns essential to life that has only a partial overlap with complex systems theory,[7]。因此,CBS是一个旨在发现和建模生命所必需的关系模式理论科学领域,它只与复杂系统理论和被称为系统生物学的生物学的系统方法有部分重叠;这是因为后者主要局限于生物组织和有机体的简化模型,以及对与生物学复杂性相关的哲学或语义问题的一般性考虑。此外,人们把广泛的抽象理论复杂系统作为应用数学的一个领域进行研究,无论其是否与生物学、化学或物理相关。
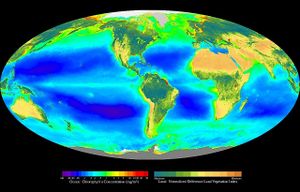
生物体和生物圈的复杂性
研究人员一直困扰于如何完整定义单个生物体、物种、生态系统、生物进化和生物圈的复杂性,而且这仍然是一个悬而未决的问题[3][8]。
大多数复杂系统模型通常是根据统计物理学、信息论和非线性动力学的概念来制定的;这些方法并不关注或者说不包括与组织、拓扑属性或代数拓扑有关的复杂性的概念部分,如基因组、交互体和生物有机体的网络连通性这些重要概念[6][9][10]。近年来,人们把以信息论、网络拓扑/抽象图论概念为基础的两种互补方法在神经科学和人类认知等领域结合起来[7][11]。人们普遍认为,组织的复杂程度存在一种应与本体论的现实层次相区别层次结构[7][12][13],现代等级分类的分类方法也承认生物圈的例如:生物领域和生物圈、生物的界、门、纲、目、科、属和种等复杂层次结构。由于生物体具有动态性和组成的可变性、内在的“模糊性”、自生属性、自我繁殖的能力等等,生物体不符合一般系统的“标准”的定义,因此它们在功能和结构上都是“超级复杂”的;因此,在CSB中,生物体只能被定义为一种简单动态系统,“元系统”[7][14]。这样一个有机体、物种、“生态系统”等等的元系统定义 ,如自生系统理论中所述的系统的系统[15]。它也不同于K·D·帕尔默在元系统工程中提出的定义[16],即生物体不同于具有固定输入输出转换函数的机器和自动机,或不同于具有固定相空间的连续动力系统[17],这与笛卡尔哲学思想相反;因此,尽管“非确定性自动机”和“模糊自动机”也被定义了,但生物体不能仅仅用五组a(状态、启动状态、输入和输出集/字母、转换函数)来定义[18]。然而,棋盘自动机 tessellation automata或元胞自动机 cellular automata 提供了一种直观的、可视化的/计算的视角来洞察较低层次的复杂性,因此已经成为一种越来越流行的离散模型,研究领域包括可计算理论、应用数学、物理、计算机科学、理论生物学/系统生物学、癌症模拟和微观结构建模。利用遗传算法[19][20][21] 实现元胞自动机是一个桥接棋盘自动机和CSB中的高层次复杂性方法之间差距的新兴领域。
复杂系统生物学的主题
以下只是复杂系统生物学所涵盖的部分主题列表:
- 生物与物种的关系与进化 Organisms and species relations and evolution
- 物种间的相互作用 Interactions among Species
- 进化论和种群遗传学 Evolution theories and population genetics
- 群体遗传学模型 Population genetics models
- 表观遗传学 Epigenetics
- 分子进化理论 Molecular evolution theories
- 量子生物计算学 Quantum biocomputation
- 量子遗传 Quantum genetics[22]
- 自我繁殖(在更一般的情况下也称为自我复制) Self-reproduction[26] (also called self-replication in a more general context)
- 计算基因模型 Computational gene models
- DNA拓扑学 DNA topology
- DNA测序理论 DNA sequencing theory
- 进化发育生物学 Evolutionary developmental biology
- 自我生产 Autopoiesis
- 蛋白质折叠 Protein folding
- 端粒酶在体内的构象和功能 Telomerase conformations and functions in vivo
- 表观遗传学 Epigenetics
- 交互组学 Interactomics[27][28]
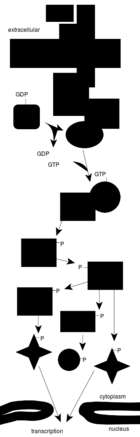
- 细胞信号传导 Cell signaling
- 信号转导网络 Signal transduction networks
- 复杂神经网络 Complex neural nets
- 基因网络 Genetic networks
- 形态发生 Morphogenesis
- 数字形态发生 Digital morphogenesis
- 复杂自适应系统 Complex adaptive system
- 形态形成的拓扑模型 Topological models of morphogenesis
- 流行病学 Epidemiology
- 理论生态学 Theoretical ecology
- 免疫系统 Immune system
另请参阅
- 数学和理论生物学 Mathematical and theoretical biology
- 抽象关系生物学 Abstract relational biology
- 复杂 Complexity
- 复杂系统 Complex system
- 生物系统 Biological system
- 系统理论 Systems theory
- 动力系统 Dynamical system
- 动力系统理论 Dynamical systems theory
- 自动机理论 Automata theory
- 元胞自动机 Cellular automaton
- 系统生物学 Systems biology
- 人类学中的系统理论 Systems theory in anthropology
- 非线性度 Nonlinearity
- 生成科学 Generative sciences
- 紧急情况 Emergence
- 生物圈 Biosphere
- 脱氧核糖核酸 DNA
- 量子生物学 Quantum biology
- 量子遗传学 Quantum genetics
- 量子生物化学 Quantum biochemistry
- 量子化学 Quantum chemistry
- 量子分子动力学 Quantum molecular dynamics
- 蛋白质折叠 Protein folding
- 基因组学 Genomics
- 蛋白质组学 Proteomics
- 表观遗传学 Epigenetics
- 复杂自适应系统 Complex adaptive system
- 多代理系统 Multi-agent systems
- 认知科学 Cognitive Science
- 面向模式的建模 Pattern oriented modeling
- 波动性,不确定性,复杂性和歧义性 Volatility, uncertainty, complexity and ambiguity
- 蓝色基因 blue Gene
- 折叠@家 Folding@home
- 端粒酶 Telomerase
- 生命是什么 What Is Life?
传记
笔记
- ↑ Sprites, P; Glymour, C; Scheines, R (2000). Causation, Prediction, and Search: Adaptive Computation and Machine Learning (2nd ed.). MIT Press.
- ↑ Donald Snooks, Graeme, "A general theory of complex living systems: Exploring the demand side of dynamics", Complexity, vol. 13, no. 6, July/August 2008.
- ↑ 3.0 3.1 Bonner, J. T. 1988. The Evolution of Complexity by Means of Natural Selection. Princeton: Princeton University Press.
- ↑ 4.0 4.1 Rosen, R. (1958a). "A Relational Theory of Biological Systems". Bulletin of Mathematical Biophysics. 20 (3): 245–260. doi:10.1007/bf02478302.
- ↑ Baianu, I. C. (2006). "Robert Rosen's Work and Complex Systems Biology". Axiomathes. 16 (1–2): 25–34. doi:10.1007/s10516-005-4204-z. S2CID 4673166.
- ↑ 6.0 6.1 Rosen, R. (1958b). "The Representation of Biological Systems from the Standpoint of the Theory of Categories". Bulletin of Mathematical Biophysics. 20 (4): 317–341. doi:10.1007/bf02477890.
- ↑ 7.0 7.1 7.2 7.3 Baianu, I. C.; Brown, R.; Glazebrook, J. F. (2007). "Categorical Ontology of Complex Spacetime Structures: The Emergence of Life and Human Consciousness". Axiomathes. 17 (3–4): 223–352. CiteSeerX 10.1.1.145.9486. doi:10.1007/s10516-007-9011-2. S2CID 123179302.
- ↑ Heylighen, Francis (2008). "Complexity and Self-Organization". In Bates, Marcia J.; Maack, Mary Niles. Encyclopedia of Library and Information Sciences. CRC.
- ↑ ^ Heylighen, Francis (2008). "Complexity and Self-Organization". In Bates, Marcia J.; Maack, Mary Niles. Encyclopedia of Library and Information Sciences. CRC.
- ↑ "abstract relational biology (ARB)". PlanetPhysics. Retrieved 2010-03-17.
- ↑ http://hdl.handle.net/10101/npre.2011.6115.1 Wallace, Rodrick. When Spandrels Become Arches: Neural crosstalk and the evolution of consciousness. Available from Nature Precedings (2011)
- ↑ Poli R (2001a). "The Basic Problem of the Theory of Levels of Reality". Axiomathes. 12 (3–4): 261–283. doi:10.1023/A:1015845217681. S2CID 55743057.
- ↑ Poli R (1998). "Levels". Axiomathes. 9 (1–2): 197–211. doi:10.1007/bf02681712. PMID 8053082.
- ↑ Metasystem Transition Theory, Valentin Turchin, Cliff Joslyn, 1993-1997
- ↑ Reflexive Autopoietic Systems Theory
- ↑ Meta-system Engineering, Kent D. Palmer, 1996
- ↑ Hoff, M.A., Roggia, K.G., Menezes, P.B.:(2004). Composition of Transformations: A Framework for Systems with Dynamic Topology. International Journal of Computing Anticipatory System's 14:259–270
- ↑ Hoff, M.A., Roggia, K.G., Menezes, P.B.:(2004). Composition of Transformations: A Framework for Systems with Dynamic Topology. International Journal of Computing Anticipatory System's 14:259–270
- ↑ The Evolutionary Design of Collective Computation in Cellular Automata, James P. Crutchfeld, Melanie Mitchell, Rajarshi Das (In J. P. Crutchfield and P. K. Schuster (editors), Evolutionary Dynamics|Exploring the Interplay of Selection, Neutrality, Accident, and Function. New York: Oxford University Press, 2002.)
- ↑ Evolving Cellular Automata with Genetic Algorithms: A Review of Recent Work, Melanie Mitchell, James P. Crutchfeld, Rajarshi Das (In Proceedings of the First International Conference on Evolutionary Computation and Its Applications (EvCA'96). Moscow, Russia: Russian Academy of Sciences, 1996.)
- ↑ Peak, West; Messinger, Mott; Messinger, SM; Mott, KA (2004). "Evidence for complex, collective dynamics and emergent, distributed computation in plants". Proceedings of the National Academy of Sciences of the USA. 101 (4): 918–922. Bibcode:2004PNAS..101..918P. doi:10.1073/pnas.0307811100. PMC 327117. PMID 14732685.
- ↑ Rosen, R. 1960. (1960). "A quantum-theoretic approach to genetic problems". Bulletin of Mathematical Biophysics. 22 (3): 227–255. doi:10.1007/BF02478347.
- ↑ Baianu, I. C.: 2006 (2006). "Robert Rosen's Work and Complex Systems Biology". Axiomathes. 16 (1–2): 25–34. doi:10.1007/s10516-005-4204-z.
- ↑ Rosen, R.: 1958b (1958). "The Representation of Biological Systems from the Standpoint of the Theory of Categories". Bulletin of Mathematical Biophysics. 20 (4): 317–341. doi:10.1007/BF02477890.
- ↑ PlanetMath
- ↑ "PlanetMath". PlanetMath. Retrieved 2010-03-17.
- ↑ 27.0 27.1 Faith, JJ; et al. (2007). "Large-Scale Mapping and Validation of Escherichia coli Transcriptional Regulation from a Compendium of Expression Profiles". PLOS Biology. 5 (1): 54–66. doi:10.1371/journal.pbio.0050008. PMC 1764438. PMID 17214507.
- ↑ 28.0 28.1 Hayete, B; Gardner, TS; Collins, JJ (2007). "Size matters: network inference tackles the genome scale". Molecular Systems Biology. 3 (1): 77. doi:10.1038/msb4100118. PMC 1828748. PMID 17299414.
参考文献引用
- Ahmed, E. (2006). "On modeling the immune system as a complex system". Theor. BioSci. 124 (3–4): 413–8. arXiv:0801.0847. Bibcode:2008arXiv0801.0847A. doi:10.1016/j.thbio.2005.07.001. PMID 17046369.
- Baianu, I. C., Computer Models and Automata Theory in Biology and Medicine., Monograph, Ch.11 in M. Witten (Editor), Mathematical Models in Medicine, vol. 7., Vol. 7: 1513-1577 (1987),Pergamon Press:New York, (updated by Hsiao Chen Lin in 2004
- Bonner, J. T. 1988. The Evolution of Complexity by Means of Natural Selection. Princeton: Princeton University Press.
- Donald Snooks, Graeme, "A general theory of complex living systems: Exploring the demand side of dynamics", Complexity, vol. 13, no. 6, July/August 2008.
- Drazin, P.G., Nonlinear systems. C.U.P., 1992.
- Edelstein-Keshet, L., Mathematical Models in Biology. SIAM, 2004.
- Forgacs, G.; S. A. Newman, Biological Physics of the Developing Embryo. C.U.P., 2005.
- Israel G (1988). "On the contribution of Volterra and Lotka to the development of modern biomathematics". History and Philosophy of the Life Sciences. 10 (1): 37–49. PMID 3045853.
- Israel, G., 2005, "Book on mathematical biology" in Grattan-Guinness, I., ed., Landmark Writings in Western Mathematics. Elsevier: 936-44.
- Jordan, D.W.; Smith, P., Nonlinear ordinary differential equations, 2nd ed. O.U.P., 1987.
- Kampen, N.G. van. Stochastic Processes in Physics and Chemistry, North Holland., 3rd ed. 2001,
- Murray, J.D., Mathematical Biology. Springer-Verlag, 3rd ed. in 2 vols.: Mathematical Biology: I. An Introduction, 2002 ; Mathematical Biology: II. Spatial Models and Biomedical Applications, 2003 .
- Nicolas Rashevsky. (1938)., Mathematical Biophysics. Chicago: University of Chicago Press.
- Preziosi, L., Cancer Modelling and Simulation. Chapman Hall/CRC Press, 2003..
- Renshaw, E., Modelling biological populations in space and time. C.U.P., 1991.
- Rosen, Robert.1991, Life Itself: A Comprehensive Inquiry into the Nature, Origin, and Fabrication of Life, Columbia University Press, published posthumously:
- Rosen, Robert .1970. Dynamical system theory in biology. New York, Wiley-Interscience.
- Rosen, Robert. 2000, Essays on Life Itself, Columbia University Press.
- Rosen, Robert. 2003, "Anticipatory Systems; Philosophical, Mathematical, and Methodolical Foundations", Rosen Enterprises publs.
- Rubinow, S.I., Introduction to mathematical biology. John Wiley, 1975.
- Scudo FM (March 1971). "Vito Volterra and theoretical ecology". Theoretical Population Biology. 2 (1): 1–23. doi:10.1016/0040-5809(71)90002-5. PMID 4950157.
- Segel, L.A., Modeling dynamic phenomena in molecular and cellular biology. C.U.P., 1984..
- Strogatz, S.H., Nonlinear dynamics and Chaos: Applications to Physics, Biology, Chemistry, and Engineering. Perseus, 2001,
- Thompson, D'Arcy W., 1992. On Growth and Form. Dover reprint of 1942, 2nd ed. (1st ed., 1917).
进一步阅读
- Drawing the Line Between Theoretical and Basic Biology, a forum article by Isidro A. T. Savillo
- Kurata, Hiroyuki; Taira, K; Kitano, H (1999). "Synthesis and Analysis of a Biological System". Genome Informatics Series (Sers 10): 352–353. OCLC 203735966.