|
|
| 第1行: |
第1行: |
| − | 此词条暂由小竹凉翻译,未经人工整理和审校,带来阅读不便,请见谅。
| |
| − | 由CecileLi初步审校{{Unreferenced|date=February 2011}}于2020.11.19再次审校,若有遗漏敬请谅解
| |
| | | | |
| | | | |
| | + | 在'''<font color="#ff8000">物理学领域 Physics</font>'''中,'''有序'''和'''无序'''指的是多粒子系统中某种'''<font color="#ff8000">对称性 symmetry</font>'''或'''<font color="#ff8000">相关性 correlation</font>'''的存在性问题。 |
| | | | |
| − | In [[physics]], the terms '''order''' and '''disorder''' designate the presence or absence of some [[symmetry]] or [[correlation]] in a many-particle system.
| |
| | | | |
| − | In physics, the terms order and disorder designate the presence or absence of some symmetry or correlation in a many-particle system.
| + | 在'''<font color="#ff8000">凝聚态物理学 condensed matter physics</font>'''中,系统通常在低温下有序;受热后,它们会经历一个或几个'''<font color="#ff8000">相变 Phase Transition</font>'''进入无序状态。 |
| | | | |
| − | 在'''<font color="#ff8000">物理学领域 Physics</font>'''中,'''有序'''和'''无序'''指的是多粒子系统中某种'''<font color="#ff8000">对称性 Symmetry</font>'''或'''<font color="#ff8000">相关性 Correlation</font>'''的存在性问题。
| |
| | | | |
| | + | 这种'''有序-无序转变'''的例子有: |
| | | | |
| | + | * 冰的融化: 固-液转变后,有序变无序; |
| | | | |
| | + | * 铁在受到'''<font color="#ff8000">居里温度 Curie Temperature</font>'''以上温度加热时就会逐渐退磁:铁磁性-顺磁性转变,磁有序变无序。 |
| | | | |
| | | | |
| − | In [[condensed matter physics]], systems typically are ordered at low temperatures; upon heating, they undergo one or several [[phase transition]]s into less ordered states.
| + | 有序或无序的自由度可以是平移('''<font color="#ff8000">晶体 crystal</font>'''有序)、旋转('''<font color="#ff8000">铁电性 ferroelectric</font>'''有序)或自旋状态('''<font color="#ff8000">磁性 Magnetic</font>'''有序)。 |
| | | | |
| − | In condensed matter physics, systems typically are ordered at low temperatures; upon heating, they undergo one or several phase transitions into less ordered states.
| |
| | | | |
| − | 在'''<font color="#ff8000">凝聚态物理学 Condensed Matter Physics</font>'''中,系统通常在低温下有序; 受热后,它们会经历一个或几个'''<font color="#ff8000">相变 Phase Transition</font>'''进入无序状态。
| + | 这种顺序既可以是完全晶体'''<font color="#ff8000">空间群 space group</font>'''的对称的也可以是关联的。根据相关系数随距离衰减的程度,我们可以说'''<font color="#ff8000">长程有序 long range order</font>'''或'''<font color="#ff8000">短程有序 short range order</font>'''。 |
| | | | |
| − | Examples for such an '''order-disorder transition''' are:
| |
| | | | |
| − | Examples for such an order-disorder transition are:
| + | 如果一个无序的状态不存在于'''<font color="#ff8000">热力学平衡 thermodynamic equilibrium</font>'''之中,那么就是'''淬致无序'''。例如,'''<font color="#ff8000">玻璃 glass</font>'''是通过淬火('''<font color="#ff8000">过冷却 supercooling</font>''')液体获得的。推而广之,其它淬火态称为'''<font color="#ff8000">自旋玻璃 spin glass</font>'''、'''<font color="#ff8000">取向玻璃 orientational glass</font>'''。在某些情况下,淬致无序的对立面是'''退火无序'''。 |
| | | | |
| − | 这种'''有序-无序转变'''的例子有:
| |
| | | | |
| − | * the melting of ice: solid-liquid transition, loss of crystalline order;
| + | ==特征化秩序 Characterizing order== |
| − | 冰的融化: 固-液转变后会失去结晶秩序
| + | ===晶格周期性与 x 射线结晶度 Lattice periodicity and X-ray crystallinity=== |
| | | | |
| | + | 固体中最严格的秩序形式是'''晶格周期性''':某种模式( 即'''<font color="#ff8000">单元格 unit cell</font>''' 中原子的排列)一次又一次地重复,通过平移形成一个不变的空间'''<font color="#ff8000">平铺 tiling</font>'''。这就是'''<font color="#ff8000">晶体 crystal</font>'''的定义属性。可能的对称性已在14个'''<font color="#ff8000">布拉维斯晶格 bravais lattice</font>'''和230个'''<font color="#ff8000">空间群 space group</font>'''中进行了分类。 |
| | | | |
| − | * the demagnetization of iron by heating above the [[Curie temperature]]: ferromagnetic-paramagnetic transition, loss of magnetic order.
| |
| − | 铁在'''<font color="#ff8000">受到居里点 Curie Temperature</font>'''以上温度加热时就会逐渐退磁: 铁磁-顺磁转变时会导致磁有序的耗损。
| |
| | | | |
| | + | 格点周期性意味着'''长程有序''':如果我们只知道一个单位单元,那么借助于平移对称性,就有可能在任意距离上精确地预测所有原子的位置。在20世纪的大部分时间里,相反的情况也被认为是合理的——但直到1982年'''<font color="#ff8000">准晶体 quasicrystal</font>'''的发现表明,完全确定性的倾斜并不具有晶格周期性。 |
| | | | |
| | | | |
| | + | 除了结构有序外,还有'''电荷有序 charge ordering'''、'''自旋有序 spin ordering'''、'''磁有序 magnetic ordering'''和成分有序。磁有序可以在'''<font color="#ff8000">中子衍射 neutron diffraction</font>'''中观察到。 |
| | | | |
| | | | |
| | + | 这是一个热力学'[[熵 Entropy]]的概念,通常表现为一个二阶'''<font color="#ff8000">相变 phase transition</font>'''。一般来说,高热能与无序有关,低热能与有序有关,但有违背这一规律的现象存在。在低能衍射实验中,有序峰十分明显。 |
| | | | |
| − | The degree of freedom that is ordered or disordered can be translational ([[crystal]]line ordering), rotational ([[ferroelectricity|ferroelectric]] ordering), or a spin state ([[magnetism|magnetic]] ordering).
| |
| | | | |
| − | The degree of freedom that is ordered or disordered can be translational (crystalline ordering), rotational (ferroelectric ordering), or a spin state (magnetic ordering).
| + | ===远程有序 Long-range order=== |
| | | | |
| − | 有序或无序的自由度可以是平移('''<font color="#ff8000">晶体 Crystal</font>'''有序)、旋转('''<font color="#ff8000">铁电性 ferroelectric</font>'''有序)或自旋状态('''<font color="#ff8000">磁性 Magnetic</font>'''有序)。
| + | '''远程有序'''描述了同一样本的远程部分表现出相关行为的物理系统。 |
| | | | |
| | | | |
| | + | 这可以用'''<font color="#ff8000">相关函数 correlation function</font>'''(量子场论)来表示,即'''<font color="#ff8000">旋转相关函数 spin-spin correlation Function</font>'''(量子场论): |
| | | | |
| | | | |
| | + | :<math>G(x,x') = \langle s(x),s(x') \rangle. \, </math> |
| | | | |
| − | The order can consist either in a full crystalline [[space group]] symmetry, or in a correlation. Depending on how the correlations decay with distance, one speaks of [[long range order]] or [[short range order]].
| |
| − |
| |
| − | The order can consist either in a full crystalline space group symmetry, or in a correlation. Depending on how the correlations decay with distance, one speaks of long range order or short range order.
| |
| − |
| |
| − | 这种顺序既可以是完全晶体'''<font color="#ff8000">空间群 Space Group</font>'''的对称的也可以是关联的。根据相关系数随距离衰减的程度,我们可以说'''<font color="#ff8000">长程有序 Long Range Order</font>'''或'''<font color="#ff8000">短程有序 Short Range Order</font>'''。
| |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − | If a disordered state is not in [[thermodynamic equilibrium]], one speaks of '''quenched disorder'''. For instance, a [[glass]] is obtained by quenching ([[supercooling]]) a liquid. By extension, other quenched states are called [[spin glass]], [[orientational glass]]. In some contexts, the opposite of quenched disorder is '''annealed disorder'''.
| |
| − |
| |
| − | If a disordered state is not in thermodynamic equilibrium, one speaks of quenched disorder. For instance, a glass is obtained by quenching (supercooling) a liquid. By extension, other quenched states are called spin glass, orientational glass. In some contexts, the opposite of quenched disorder is annealed disorder.
| |
| − |
| |
| − | 如果一个无序的状态不存在于'''<font color="#ff8000">热力学平衡 Thermodynamic Equilibrium</font>'''之中,那么就是'''淬致无序'''。例如,'''<font color="#ff8000">玻璃 Glass</font>'''是通过淬火('''<font color="#ff8000">过冷却 Supercooling</font>''')液体获得的。推而广之,其它淬火态称为'''<font color="#ff8000">自旋玻璃 Spin Glass</font>'''、'''<font color="#ff8000">取向玻璃 Orientational Glass</font>'''。在某些情况下,淬致无序的对立面是'''退火无序'''。
| |
| − |
| |
| − | ==Characterizing order==
| |
| − |
| |
| − | ==Characterizing order==
| |
| − |
| |
| − | 特征化秩序
| |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − | ===Lattice periodicity and X-ray crystallinity===
| |
| − |
| |
| − | ===Lattice periodicity and X-ray crystallinity===
| |
| − |
| |
| − | '''晶格周期性与 x 射线结晶度'''
| |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − | The strictest form of order in a solid is '''lattice periodicity''': a certain pattern (the arrangement of atoms in a [[unit cell]]) is repeated again and again to form a translationally invariant [[Tessellation|tiling]] of space. This is the defining property of a [[crystal]]. Possible symmetries have been classified in 14 [[Bravais lattice]]s and 230 [[space group]]s.
| |
| − |
| |
| − | The strictest form of order in a solid is lattice periodicity: a certain pattern (the arrangement of atoms in a unit cell) is repeated again and again to form a translationally invariant tiling of space. This is the defining property of a crystal. Possible symmetries have been classified in 14 Bravais lattices and 230 space groups.
| |
| − |
| |
| − | 固体中最严格的秩序形式是'''晶格周期性''': 某种模式( '''<font color="#ff8000">即单元格 Unit Cell</font>''' 中原子的排列)一次又一次地重复,通过平移形成一个不变的空间'''<font color="#ff8000">平铺 Tiling</font>'''。这就是'''<font color="#ff8000">晶体 Crystal</font>'''的定义属性。可能的对称性已在14个'''<font color="#ff8000">布拉维斯晶格 Bravais Lattice</font>'''和230个'''<font color="#ff8000">空间群 Space Group</font>'''中进行了分类。
| |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − | Lattice periodicity implies '''long-range order''': if only one unit cell is known, then by virtue of the translational symmetry it is possible to accurately predict all atomic positions at arbitrary distances. During much of the 20th century, the converse was also taken for granted – until the discovery of [[quasicrystal]]s in 1982 showed that there are perfectly deterministic tilings that do not possess lattice periodicity.
| |
| − |
| |
| − | Lattice periodicity implies long-range order: if only one unit cell is known, then by virtue of the translational symmetry it is possible to accurately predict all atomic positions at arbitrary distances. During much of the 20th century, the converse was also taken for granted – until the discovery of quasicrystals in 1982 showed that there are perfectly deterministic tilings that do not possess lattice periodicity.
| |
| − |
| |
| − | 格点周期性意味着'''长程有序''': 如果我们只知道一个单位单元,那么借助于平移对称性,就有可能在任意距离上精确地预测所有原子的位置。在20世纪的大部分时间里,相反的情况也被认为是合理的——但直到1982年'''<font color="#ff8000">准晶体 Quasicrystal</font>'''的发现表明,完全确定性的倾斜并不具有晶格周期性。
| |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − | Besides structural order, one may consider [[charge ordering]], [[Spin (physics)|spin]] ordering, [[magnetic ordering]], and compositional ordering. Magnetic ordering is observable in [[neutron diffraction]].
| |
| − |
| |
| − | Besides structural order, one may consider charge ordering, spin ordering, magnetic ordering, and compositional ordering. Magnetic ordering is observable in neutron diffraction.
| |
| − |
| |
| − | 除了结构有序外,还可以考虑'''<font color="#ff8000">电荷有序 Charge Ordering</font>'''、'''<font color="#ff8000">自旋 Spin</font>'''有序、'''<font color="#ff8000">磁有序 Magnetic Ordering</font>'''和成分有序。磁有序可以在'''<font color="#ff8000">中子衍射 Neutron Diffraction</font>'''中观察到。
| |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − | It is a [[thermodynamic]] [[Entropy (order and disorder)|entropy]] concept often displayed by a second-order [[phase transition]]. Generally speaking, high thermal energy is associated with disorder and low thermal energy with ordering, although there have been violations of this. Ordering peaks become apparent in diffraction experiments at low energy.
| |
| − |
| |
| − | It is a thermodynamic entropy concept often displayed by a second-order phase transition. Generally speaking, high thermal energy is associated with disorder and low thermal energy with ordering, although there have been violations of this. Ordering peaks become apparent in diffraction experiments at low energy.
| |
| − |
| |
| − | 这是一个'''<font color="#ff8000">熵 Thermodynamics Entropy</font>'''的概念,通常表现为一个二阶'''<font color="#ff8000">相变 Phase Transition</font>'''。一般来说,高热能与无序有关,低热能与有序有关,但有违背这一规律的现象存在。在低能衍射实验中,有序峰十分明显。
| |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − | ===Long-range order===
| |
| − |
| |
| − | ===Long-range order===
| |
| − |
| |
| − | 远程有序
| |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − | '''Long-range order''' characterizes physical [[system]]s in which remote portions of the same sample exhibit [[correlation|correlated]] behavior.
| |
| − |
| |
| − | Long-range order characterizes physical systems in which remote portions of the same sample exhibit correlated behavior.
| |
| − |
| |
| − | '''远程有序'''描述了同一样本的远程部分表现出'''<font color="#ff8000">相关 correlated</font>'''行为的物理'''<font color="#ff8000">系统 System</font>'''。
| |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − | This can be expressed as a [[correlation function]], namely the [[spin (physics)|spin-spin correlation function]]:
| |
| − |
| |
| − | This can be expressed as a correlation function, namely the spin-spin correlation function:
| |
| − |
| |
| − | 这可以用'''<font color="#ff8000">相关函数 Correlated Function</font>'''(量子场论)来表示,即'''<font color="#ff8000">旋转相关函数 Spin-spin Correlation Function</font>'''(量子场论) :
| |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − | : <math>G(x,x') = \langle s(x),s(x') \rangle. \, </math>
| |
| − |
| |
| − | <math>G(x,x') = \langle s(x),s(x') \rangle. \, </math>
| |
| − |
| |
| − | 设: <math>G(x,x') = \langle s(x),s(x') \rangle. \, </math>
| |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − | where ''s'' is the spin quantum number and ''x'' is the distance function within the particular system.
| |
| − |
| |
| − | where s is the spin quantum number and x is the distance function within the particular system.
| |
| | | | |
| | 其中 ''s'' 是自旋量子数,''x'' 是特定系统中的距离函数。 | | 其中 ''s'' 是自旋量子数,''x'' 是特定系统中的距离函数。 |
| | | | |
| | | | |
| | + | 当<math>x=x'</math>时,这个函数等于单位数量,当距离<math>|x-x'|</math>增加时,函数值减少。通常情况下,当它在很大程度上'''<font color="#ff8000">呈指数衰减 Decays Exponentially</font>'''为零时,系统就被认为是无序的。但如果相关函数(量子场论)衰变为一个常数值,那么这个系统就被认为具有远程有序。如果它衰变成为零以作为距离的幂,那么它被称为'''准远程有序'''(详见下面引用的教科书第11章。参见'''<font color="#ff8000">Berezinskii–Kosterlitz–Thouless过渡 Berezinskii–Kosterlitz–Thouless Transition</font>''')。请注意,构成较大的<math>|x-x'|</math>的值可以理解为渐近性。 |
| | | | |
| | | | |
| | + | ==淬火无序态 Quenched disorder== |
| | | | |
| − | This function is equal to unity when <math>x=x'</math> and decreases as the distance <math>|x-x'|</math> increases. Typically, it [[exponential decay|decays exponentially]] to zero at large distances, and the system is considered to be disordered. But if the correlation function decays to a constant value at large <math>|x-x'|</math> then the system is said to possess long-range order. If it decays to zero as a power of the distance then it is called quasi-long-range order (for details see Chapter 11 in the textbook cited below. See also [[Kosterlitz-Thouless transition|Berezinskii–Kosterlitz–Thouless transition]]). Note that what constitutes a large value of <math>|x-x'|</math> is understood in the sense of [[asymptotic analysis|asymptotics]].
| + | 在[[统计物理学 statistical physics]]中,当定义系统行为的某些参数是不随时间演化的随机变量时,系统称为'''淬火无序态'''。它们被'''<font color="#ff8000">淬火 quenched</font>'''或者''冷冻 frozen''。'''<font color="#ff8000">自旋玻璃态 spin glass</font>'''就是一个典型的例子。与'''<font color="#ff8000">退火无序态 annealed disorder</font>'''相反,它允许随机变量的自我进化。 |
| − | | |
| − | This function is equal to unity when <math>x=x'</math> and decreases as the distance <math>|x-x'|</math> increases. Typically, it decays exponentially to zero at large distances, and the system is considered to be disordered. But if the correlation function decays to a constant value at large <math>|x-x'|</math> then the system is said to possess long-range order. If it decays to zero as a power of the distance then it is called quasi-long-range order (for details see Chapter 11 in the textbook cited below. See also Berezinskii–Kosterlitz–Thouless transition). Note that what constitutes a large value of <math>|x-x'|</math> is understood in the sense of asymptotics.
| |
| − | | |
| − | 当<math>x=x'</math>时,这个函数等于单位数量,当距离<math>|x-x'|</math>增加时,函数值减少。通常情况下,当它在很大程度上'''<font color="#ff8000">呈指数衰减 Decays Exponentially</font>'''为零时,系统就被认为是无序的。但如果相关函数(量子场论)衰变为一个常数值,那么这个系统就被认为具有远程有序。如果它衰变成为零以作为距离的幂,那么它被称为准远程有序(详见下面引用的教科书第11章)。参见'''<font color="#ff8000">Berezinskii–Kosterlitz–Thouless过渡 Berezinskii–Kosterlitz–Thouless Transition</font>''')。请注意,构成较大的<math>|x-x'|</math>的值可以理解为渐近性。
| |
| − | | |
| − | ==Quenched disorder==
| |
| − | | |
| − | ==Quenched disorder==
| |
| − | | |
| − | 淬致无序
| |
| − | | |
| − | | |
| − | | |
| − | | |
| − | | |
| − | In [[statistical physics]], a system is said to present '''quenched disorder''' when some parameters defining its behavior are [[Random variable|random variables]] which do not evolve with time, i.e. they are [[quenching|quenched]] or ''frozen''. [[Spin glass]]es are a typical example. It is opposite to [[annealed disorder]], where the random variables are allowed to evolve themselves.
| |
| − | | |
| − | In statistical physics, a system is said to present quenched disorder when some parameters defining its behavior are random variables which do not evolve with time, i.e. they are quenched or frozen. Spin glasses are a typical example. It is opposite to annealed disorder, where the random variables are allowed to evolve themselves.
| |
| − | | |
| − | 在'''<font color="#ff8000">统计物理学 Statistical Physics</font>'''中,当定义系统行为的某些参数是不随时间演化的'''<font color="#ff8000">随机变量 Random Variable</font>'''时,系统称为淬致无序。它们被'''<font color="#ff8000">淬火 Quenched</font>'''或者''冷冻''。'''<font color="#ff8000">自旋玻璃 Spin Glass</font>'''就是一个典型的例子。与'''<font color="#ff8000">退火无序 Annealed Disorder</font>'''相反,它允许随机变量的自我进化。
| |
| − | | |
| − | | |
| − | | |
| − | | |
| − | | |
| − | In mathematical terms, quenched disorder is harder to analyze than its annealed counterpart, since the thermal and the noise averaging play very different roles. In fact, the problem is so hard that few techniques to approach each are known, most of them relying on approximations. The most used are
| |
| − | | |
| − | In mathematical terms, quenched disorder is harder to analyze than its annealed counterpart, since the thermal and the noise averaging play very different roles. In fact, the problem is so hard that few techniques to approach each are known, most of them relying on approximations. The most used are
| |
| − | | |
| − | 在数学中,由于热平均和噪声通常起着非常不同的作用,淬致无序比退火无序更难分析。事实上,这个问题太过困难以至于很少有已知的技术可以处理,而现有的大多数解决方案都依赖于近似值。最常用的是
| |
| − | | |
| − | | |
| − | | |
| − | | |
| − | | |
| − | # a technique based on a mathematical analytical continuation known as the [[replica trick]]
| |
| − | | |
| − | a technique based on a mathematical analytical continuation known as the replica trick
| |
| − | | |
| − | 一种基于数学解析延拓的技术,被称为'''<font color="#ff8000">复制技巧 Replica Trick</font>'''
| |
| − | | |
| − | # the [[Cavity method]]; although these give results in accord with experiments in a large range of problems, they are not generally proven to be a rigorous mathematical procedure.
| |
| − | | |
| − | the Cavity method; although these give results in accord with experiments in a large range of problems, they are not generally proven to be a rigorous mathematical procedure.
| |
| − | | |
| − | '''<font color="#ff8000">谐振腔法 Cavity Method</font>'''
| |
| − | the Cavity method 谐振腔法
| |
| | | | |
| − | 虽然这些方法给出的结果与许多问题的实验结果相一致,但它们通常不是一个可证明的严格数学过程。
| |
| | | | |
| − | More recently it has been shown by rigorous methods, however, that at least in the archetypal spin-glass model (the so-called [[Spin_glass#The_model_of_Sherrington_and_Kirkpatrick|Sherrington–Kirkpatrick model]]) the replica based solution is indeed exact.
| + | 在数学中,由于热平均和噪声通常起着非常不同的作用,淬致无序比退火无序更难分析。事实上,这个问题太过困难以至于很少有已知的技术可以处理,而现有的大多数解决方案都依赖于近似值。最常用的是: |
| | | | |
| − | More recently it has been shown by rigorous methods, however, that at least in the archetypal spin-glass model (the so-called Sherrington–Kirkpatrick model) the replica based solution is indeed exact.
| |
| | | | |
| − | 然而,最近人们已经通过严密的方法证明,至少在典型的自旋玻璃模型(所谓的 '''<font color="#ff8000">Sherrington–Kirkpatrick 模型 Sherrington–Kirkpatrick Model</font>''')中,基于复制的解确实是精确的。
| + | # 一种基于数学解析延拓的技术,被称为'''<font color="#ff8000">复制技巧 Replica Trick</font>''' |
| | | | |
| | + | # '''<font color="#ff8000">谐振腔法 Cavity Method</font>''':虽然这些方法给出的结果与许多问题的实验结果相一致,但它们通常不是一个可证明的严格数学过程。 |
| | | | |
| | | | |
| | + | 然而,最近人们已经通过严密的方法证明,至少在典型的自旋玻璃模型(所谓的 '''<font color="#ff8000">Sherrington–Kirkpatrick 模型 Sherrington–Kirkpatrick Model</font>''')中,基于复制的解确实是精确的。 |
| | | | |
| − |
| |
| − | The second most used technique in this field is [[generating functional analysis]]. This method is based on [[Path integral formulation|path integrals]], and is in principle fully exact, although generally more difficult to apply than the replica procedure.
| |
| − |
| |
| − | The second most used technique in this field is generating functional analysis. This method is based on path integrals, and is in principle fully exact, although generally more difficult to apply than the replica procedure.
| |
| | | | |
| | 该领域次常用的技术是'''<font color="#ff8000">生成函数分析 Generating Functional Analysis</font>'''。这种方法是基于'''<font color="#ff8000">路线积分 Path Integrals</font>'''的,虽然这通常比复制过程更难应用,但原则上是完全精确的, | | 该领域次常用的技术是'''<font color="#ff8000">生成函数分析 Generating Functional Analysis</font>'''。这种方法是基于'''<font color="#ff8000">路线积分 Path Integrals</font>'''的,虽然这通常比复制过程更难应用,但原则上是完全精确的, |
| | | | |
| | | | |
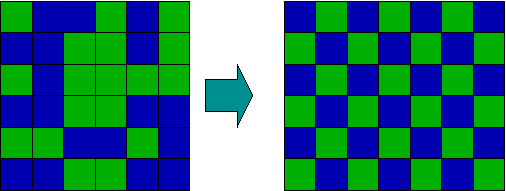
| | + | [[Image:Ordering.png|thumbnail|600px|center|从无序(左)状态过渡到有序(右)状态]] |
| | | | |
| | | | |
| − | [[Image:Ordering.png|thumbnail|600px|center|Transition from disordered (left) to ordered (right) states 从无序(左)状态过渡到有序(右)状态]]
| + | ==退火无序态 Annealed disorder== |
| | | | |
| − | Transition from disordered (left) to ordered (right) states
| + | 当一个系统的某些参数进入其定义为随机变量时,称系统呈现'''退火无序态''',但其演化与定义系统的[[自由度 Degrees of Freedom]]有关。它的定义与淬致无序相反,在淬灭无序态中,随机变量可能不会改变其值。 |
| | | | |
| − | 从无序(左)状态过渡到有序(右)状态
| |
| | | | |
| − | ==Annealed disorder== | + | 退火无序系统通常被认为更容易在数学上处理,因为无序系统的平均值和'''<font color="#ff8000">热平均值 thermal average</font>'''可以在同一基础上处理。 |
| | | | |
| − | ==Annealed disorder==
| |
| | | | |
| − | 退火无序
| + | ==参见== |
| | | | |
| | + | *在'''<font color="#ff8000">高能物理学 High Energy Physics</font>'''中,'''<font color="#ff8000">量子色动力学 Quantum Chromodynamics</font>'''中'''<font color="#ff8000">手性凝聚物 Chiral Condensate</font>'''的形成是一个有序转变,用'''<font color="#ff8000">超选择 Superselection</font>'''来讨论 |
| | + | * [[熵 Entropy]] |
| | + | * [[拓扑有序 Topological order]] |
| | + | * [[杂质 Impurity]] |
| | + | * [[上层建筑(物理学) superstructure (physics)]] |
| | | | |
| | | | |
| | + | ==延伸阅读== |
| | | | |
| | + | * H Kleinert: [http://www.physik.fu-berlin.de/~kleinert/kleiner_reb1 ''Gauge Fields in Condensed Matter''] ({{ISBN|9971-5-0210-0}}, 2 volumes) Singapore: World Scientific (1989). |
| | | | |
| − | A system is said to present '''annealed disorder''' when some parameters entering its definition are [[random variable]]s, but whose evolution is related to that of the [[Degrees of freedom (physics and chemistry)|degrees of freedom]] defining the system. It is defined in opposition to quenched disorder, where the random variables may not change their values.
| |
| − |
| |
| − | A system is said to present annealed disorder when some parameters entering its definition are random variables, but whose evolution is related to that of the degrees of freedom defining the system. It is defined in opposition to quenched disorder, where the random variables may not change their values.
| |
| − |
| |
| − | 当一个系统的某些参数进入其定义为'''<font color="#ff8000">随机变量 Random Variable</font>'''时,称系统呈现'''退火无序''',但其演化与定义系统的'''<font color="#ff8000">自由度 Degrees of Freedom</font>'''有关。它的定义与淬致无序相反,在淬灭无序中,随机变量可能不会改变其值。
| |
| | | | |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − | Systems with annealed disorder are usually considered to be easier to deal with mathematically, since the average on the disorder and the [[thermal average]] may be treated on the same footing.
| |
| − |
| |
| − | Systems with annealed disorder are usually considered to be easier to deal with mathematically, since the average on the disorder and the thermal average may be treated on the same footing.
| |
| − |
| |
| − | 退火无序系统通常被认为更容易在数学上处理,因为无序系统的平均值和'''<font color="#ff8000">热平均值 Thermal Average</font>'''可以在同一基础上处理。
| |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − | ==See also==
| |
| − |
| |
| − | ==See also 另请参见==
| |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − | * In [[high energy physics]], the formation of the [[chiral condensate]] in [[quantum chromodynamics]] is an ordering transition; it is discussed in terms of [[superselection]].
| |
| − | 在'''<font color="#ff8000">高能物理学 High Energy Physics</font>'''中,'''<font color="#ff8000">量子色动力学 Quantum Chromodynamics</font>'''中'''<font color="#ff8000">手性凝聚物 Chiral Condensate</font>'''的形成是一个有序转变,用'''<font color="#ff8000">超选择 Superselection</font>'''来讨论
| |
| − |
| |
| − |
| |
| − | * [[Entropy]]
| |
| − | 熵
| |
| − |
| |
| − |
| |
| − | * [[Topological order]]
| |
| − | '''<font color="#ff8000">拓扑有序 Topological Order</font>'''
| |
| − |
| |
| − |
| |
| − | * [[Impurity]]
| |
| − | '''<font color="#ff8000">杂质 Impurity</font>'''
| |
| − |
| |
| − |
| |
| − | * [[superstructure (physics)]]
| |
| − | '''<font color="#ff8000">上层建筑(物理学) Superstructure (physics)</font>'''
| |
| | | | |
| | == 编者推荐 == | | == 编者推荐 == |
| 第313行: |
第106行: |
| | 数十年以来,凝聚态物理学都是物理学领域中最大的分支,但是凝聚态物理学的成就直到最近才得以彰显。 | | 数十年以来,凝聚态物理学都是物理学领域中最大的分支,但是凝聚态物理学的成就直到最近才得以彰显。 |
| | | | |
| − | <br/>
| |
| − | ----
| |
| | | | |
| − | == Further reading ==
| |
| | | | |
| − | == Further reading 延伸阅读==
| + | <br/> |
| − | | |
| − | | |
| − | | |
| − | | |
| − | | |
| − | * H Kleinert: [http://www.physik.fu-berlin.de/~kleinert/kleiner_reb1 ''Gauge Fields in Condensed Matter''] ({{ISBN|9971-5-0210-0}}, 2 volumes) Singapore: World Scientific (1989).
| |
| − | | |
| − | | |
| − | | |
| − | | |
| − | | |
| − | | |
| − | | |
| − | [[Category:Statistical mechanics]]
| |
| − | | |
| − | Category:Statistical mechanics
| |
| − | | |
| − | 类别: 统计力学
| |
| − | | |
| − | [[Category:Crystallography]]
| |
| | | | |
| − | Category:Crystallography
| |
| | | | |
| − | 类别: 结晶学
| |
| | | | |
| − | <noinclude>
| + | [[Category:统计力学]] |
| | + | [[Category:结晶学]] |
| | | | |
| − | <small>This page was moved from [[wikipedia:en:Order and disorder]]. Its edit history can be viewed at [[有序和无序/edithistory]]</small></noinclude>
| |
| | | | |
| − | [[Category:待整理页面]]
| + | 小竹凉,CecileLi |