“图动力系统”的版本间的差异

2020年11月30日 (一) 17:06的版本

在数学领域中， 图动态系统 Graph dynamical systems的概念可以用来捕捉发生在图或网络上的广泛的过程。Gds 数学和计算分析的一个主题是将它们的结构特性联系起来(如网络连接)和全球动力学的结果。

Gdss 的工作是研究有限图和有限状态空间。因此，研究通常涉及到的技术是图论，组合学，代数和动力系统，而不是微分几何。原则上，我们可以在一个无限图上定义和研究 gds (例如:。元胞自动机或概率元胞自动机在 [math]\displaystyle{ mathbb { z } ^ k }[/math]或相互作用的粒子系统(包括一些随机性)上，以及具有无限状态空间的 gds (例如:在耦合映象格子中的 [math]\displaystyle{ mathbb {r} }[/math]; 例如，见 Wu。^[1]在下文中，除非另有说明，否则一切图和空间都默认为有限。

正式定义

图动力系统 Graph dynamical systems是由以下部分构成的:

具有变量集v[Y] = {1,2, ... , n}的有限图 Y。根据上下文，可以为有向图或无向图。

Y的取自有限集合“K”的每个顶点v的状态，“系统状态”是“n”元组“x”= (x₁, x₂, ... , x_n)，“x”[“v”]是由与垂直相关的状态组成的元组。

每个顶点v的顶点函数f_v 。顶点函数将时间“t”的顶点“v”的状态映射到时间t + 1 ，1基于与“Y”中“v”的1邻域相关的状态。

一个“更新方案”，通过它可以实现对单个顶点状态的映射，从而得到一个映射为“F”的离散动力系统：“Kⁿ”。

动力系统的相空间是有限有向图，其顶点集为 kⁿ，有向边(x，f (x))。相空间的结构由图 y 的性质、顶点函数(f _i)_i和更新方案决定。该领域的研究试图推断相空间特性的基础上的结构的系统组成。这种分析具有局部到全局的特点。

广义细胞自动机

例如，如果新方案由应用顶点函数组成，那么我们获得广义细胞自动机 Generalized cellular automata (GCA)(CA)类。在这种情况下，整体映射 f: k ⁿ → k ⁿ 是由

[math]\displaystyle{ f(x)vv(x[v]) }[/math]

这个类别被称为广义细胞自动机 Generalized cellular automata (GCA) ，因为经典的或标准的细胞自动机通常定义和研究在正则图或网格上，并且我们通常假定顶点函数是相同的。

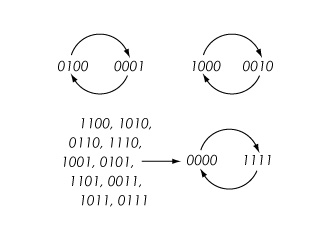
再例如: 设 y 是顶点{1,2,3,4}上的圆图，边{1,2} ，{2,3} ，{3,4}和{1,4} ，表示 Circ₄。设 k {0,1}为每个顶点的状态空间，对所有顶点函数使用 nor ₃: k ³→ k，该函数由 nor ₃ (x，y，z)(1 + x)(1 + y)(1 + z)定义，算术模为2。然后，例如，使用同步更新将系统状态(0,1,0,0)映射到(0,0,0,1)。所有的相变都显示在下面的相空间中。

序列动力系统

如果顶点函数按照 v [y]中 w (w ₁，w₂，... ，w_m)或置换[math]\displaystyle{ pi }[/math]([math]\displaystyle{ pi 1 }[/math]，[math]\displaystyle{ pi 2， dots， pi n }[/math])指定的序列异步应用，那么我们可以得到'序列动力系统 Sequential dynamical systems (SDS) 的类。^[2]在这种情况下，可以方便地引入由顶点函数构造的 y 局部映射 f_i

[math]\displaystyle{ F_i (x) = (x_1, x_2,\ldots, x_{i-1}, f_i(x[i]), x_{i+1}, \ldots , x_n) \;. }[/math]

Sds 映射 f [ f_y，w] : kⁿ → kⁿ是复合函数

[math]\displaystyle{ [F_Y ,w] = F_{w(m)} \circ F_{w(m-1)} \circ \cdots \circ F_{w(2)} \circ F_{w(1)} \;. }[/math]

如果新序列是置换序列，那么我们就经常使用置换 SDS map F = [F_Y] 以强调这一点。

例如: 设 y 是顶点{1,2,3,4}上的圆图，边{1,2} ，{2,3} ，{3,4}和{1,4} ，表示 Circ ₄。设 k {0,1}为每个顶点的状态空间，对所有顶点函数使用 nor ₃: k ³ → k，该函数由 nor ₃ (x，y，z)(1 + x)(1 + y)(1 + z)定义，算术模为2。使用新序列(1,2,3,4) ，然后将系统状态(0,1,0,0)映射到(0,0,1,0)。在所有系统状态转换下，这个动力系统依次显示在下面的相空间。

随机图动力系统

例如，从应用程序的角度来看，思考 GDS的一个或多个组件包含随机元素的情况是有趣的。激励应用程序可以包括不完全理解的过程(例如:细胞内部的动力学) ，以及所有实际应用的某些方面似乎都符合某些概率分布。还有一些由确定性原理控制的应用程序，因为它们的描述要么复杂要么笨拙，所以考虑概率近似是有意义的。

图动力系统 graph dynamical system的每个元素都可以通过几种方式随机化。例如，在顺序动力系统中，新序列可以是随机的。在每个迭代步骤中，可以从给定的新序列分布中随机选择具有相应概率的更新序列 w。新序列的匹配概率空间引出 SDS 地图的概率空间。在这方面需要研究的一个自然对象是 SDS 映射集合在状态空间上产生的 马尔可夫链 Markov chain 。这种情况被称为新序列随机 GDS，其目的如，“事件”按照一定的速率随机发生的过程(如化学反应)，在并行计算 / 离散事件模拟中的同步，以及在后面描述的计算范例中的同步! ——确保这个交叉引用保持 / 工作。

这个带有随机更新序列的具体例子说明了这类系统的两个一般事实: 当传递到一个 随机图动力系统 Stochastic graph dynamical system时，一般会导致: (1)对 马尔可夫链 Markov chain 的研究(其具体结构由 GDS 的组成部分控制) ，和(2)由此产生的 马尔可夫链 Markov chain 趋向于具有指数数量的状态。随机 GDS 研究的一个中心目标是能够推导出简化模型。

我们也可以考虑顶点函数是随机的情况，即函数是随机的 GDS。例如，随机布尔网络是函数随机 GDS 使用同步更新方案的例子，其中状态空间为 k {0,1}。有限概率 细胞自动机（PCA)是功能随机 GDS 的另一个例子。原则上，相互作用粒子系统(IPS)包括有限和无限的 PCA，但实际上，IPS 的工作主要是关注无限的情况，因为这允许在状态空间中引入更多有趣的拓扑Topologies 。

应用

图动力系统是捕捉分布式系统(如生物网络和社会网络上的传染病)的自然框架，其中许多常常被称为 复杂系统 Complex systems。

另请参见

参考文献

↑ Wu, Chai Wah (2005). "Synchronization in networks of nonlinear dynamical systems coupled via a directed graph". Nonlinearity. 18 (3): 1057–1064. Bibcode:2005Nonli..18.1057W. doi:10.1088/0951-7715/18/3/007.
↑ Mortveit, Henning S.; Reidys, Christian M. (2008). An introduction to sequential dynamical systems. Universitext. New York: Springer Verlag. ISBN 978-0-387-30654-4.

延伸阅读

Macauley, Matthew; Mortveit, Henning S. (2009). "Cycle equivalence of graph dynamical systems". Nonlinearity. 22 (2): 421–436. arXiv:0802.4412. Bibcode:2009Nonli..22..421M. doi:10.1088/0951-7715/22/2/010.

Golubitsky, Martin; Stewart, Ian (2003). The Symmetry Perspective. Basel: Birkhauser.

外部链接

Graph Dynamical Systems – A Mathematical Framework for Interaction-Based Systems, Their Analysis and Simulations by Henning Mortveit

编者推荐

集智文章推荐

动力系统中因果关系的可靠检测 | 网络科学论文速递13篇

核心速递
动力系统中因果关系的可靠检测；
抑制性突触对兴奋性神经元网络临界性的影响；
面向恶劣环境的鲁棒高效群集通信拓扑；
寻找零号病人: 医院中水平传播通道的视觉分析；
隔离期间的生产力悖论: 一个基于代理的模拟；
在线社交网络中的个人资料匹配；
复杂网络中的导航微分结构；
空间相关函数数据的空间同质性学习及其在新冠肺炎增长率曲线中的应用；
广告主意向与满意度的深度预测网络；
基于相似度和基于GNN的链接预测方法的比较研究；
共享知识的诅咒: 不完全信息协调博弈中的递归信念推理；
影响力最大化的视觉分析；
针对新冠肺炎开发人工智能解决方案的思考、良好实践、风险和陷阱；

本中文词条由水流心不竞参与编译， CecileLi 审校，不是海绵宝宝编辑，欢迎在讨论页面留言。

本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。

[wu-05-1] Wu, Chai Wah (2005). "Synchronization in networks of nonlinear dynamical systems coupled via a directed graph". Nonlinearity. 18 (3): 1057–1064. Bibcode:2005Nonli..18.1057W. doi:10.1088/0951-7715/18/3/007.

[Mortveit-08-2] Mortveit, Henning S.; Reidys, Christian M. (2008). An introduction to sequential dynamical systems. Universitext. New York: Springer Verlag. ISBN 978-0-387-30654-4.

[1]

[2]

@@ 第3行： / 第3行： @@
 |description=动力系统,代数,图论，组合数学
 }}
-在数学领域中，'''<font color="#ff8000"> 图动态系统'Graph dynamical systems</font>'''的概念可以用来捕捉发生在图或网络上的广泛的过程。Gds 数学和计算分析的一个主题是将它们的结构特性联系起来(如网络连接)和全球动力学的结果。
+在数学领域中，'''<font color="#ff8000"> 图动态系统 Graph dynamical systems</font>'''的概念可以用来捕捉发生在图或网络上的广泛的过程。Gds 数学和计算分析的一个主题是将它们的结构特性联系起来(如网络连接)和全球动力学的结果。
 Gdss 的工作是研究有限图和有限状态空间。因此，研究通常涉及到的技术是[[图论]]，[[组合学]]，[[代数]]和[[动力系统]]，而不是微分几何。原则上，我们可以在一个无限图上定义和研究 gds (例如:。元胞自动机或概率元胞自动机在 <math>mathbb { z } ^ k </math>或相互作用的粒子系统(包括一些随机性)上，以及具有无限状态空间的 gds (例如:在耦合映象格子中的 <math> mathbb {r} </math>; 例如，见 Wu。<ref name=wu-05>{{cite journal |doi=10.1088/0951-7715/18/3/007 |last=Wu |first=Chai Wah |year=2005 |title=Synchronization in networks of nonlinear dynamical systems coupled via a directed graph |journal=Nonlinearity |volume= 18 |issue= 3|pages=1057–1064 |ref=Wu:05|bibcode=2005Nonli..18.1057W }}</ref>在下文中，除非另有说明，否则一切图和空间都默认为有限。