“极限环”的版本间的差异

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
跳到导航 跳到搜索
第13行： 第13行：
  
  
−
当
+
当<math>V:\mathbb{R}^2\to\mathbb{R}^2</math>时，是一个平滑函数。这个系统的“轨迹”是满足这个微分方程的光滑函数。如果这个轨迹不是恒定的，而是返回到它的起始点，那么这个轨迹称为'''闭合'''（或周期）轨迹。如果存在一些 <math>t_0>0</math>有<math>x(t+t_0)=x(t)</math>对于所有的<math>t\in\mathbb{R}</math>。'''<font color="#ff8000">轨道 orbit</font>'''是轨迹的'''<font color="#ff8000">图像 image</font>'''，是<math>\mathbb{R}^2</math>的子集。一个“闭合轨道”，或“循环”，是一个闭合轨迹的图像。极限环是一个循环，它是其他轨迹的极限集。
−
 
 
−
 
 
−
:<math>V:\mathbb{R}^2\to\mathbb{R}^2</math>
 
−
 
 
−
 
 
−
是一个平滑函数。这个系统的“轨迹”是满足这个微分方程的光滑函数。如果这个轨迹不是恒定的，而是返回到它的起始点，那么这个轨迹称为'''闭合'''（或周期）轨迹。如果存在一些 <math>t_0>0</math>有<math>x(t+t_0)=x(t)</math>对于所有的<math>t\in\mathbb{R}</math>。'''<font color="#ff8000">轨道 orbit</font>'''是轨迹的'''<font color="#ff8000">图像 image</font>'''，是<math>\mathbb{R}^2</math>的子集。一个“闭合轨道”，或“循环”，是一个闭合轨迹的图像。极限环是一个循环，它是其他轨迹的极限集。
 
−
 
 
−
 
 
  
 
==属性==
 
==属性==

2021年1月10日 (日) 21:14的版本

此词条暂小竹凉翻译，翻译字数共657，未经人工整理和审校，带来阅读不便，请见谅。

稳定极限环和另外两个螺旋进入它的轨迹
范德波尔振荡器 Van der Pol oscillator的稳定极限环

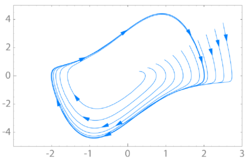
在数学中，二维相空间 phase space 动力系统的研究中，极限环是一个在相空间中的闭合轨迹，它具有当时间趋于无穷大或时间趋于负无穷大时至少有一条其他轨迹螺旋进入的性质。这种行为在一些非线性系统中表现出来。极限环已经被用来模拟许多实际振动系统的行为。对极限环的研究是由亨利·庞加莱 Henri poincaré提出的。


定义

我们认为一个二维动力系统的形式如下：

[math]\displaystyle{ x'(t)=V(x(t)) }[/math]


当[math]\displaystyle{ V:\mathbb{R}^2\to\mathbb{R}^2 }[/math]时，是一个平滑函数。这个系统的“轨迹”是满足这个微分方程的光滑函数。如果这个轨迹不是恒定的，而是返回到它的起始点，那么这个轨迹称为闭合（或周期）轨迹。如果存在一些 [math]\displaystyle{ t_0\gt 0 }[/math]有[math]\displaystyle{ x(t+t_0)=x(t) }[/math]对于所有的[math]\displaystyle{ t\in\mathbb{R} }[/math]。轨道 orbit是轨迹的图像 image，是[math]\displaystyle{ \mathbb{R}^2 }[/math]的子集。一个“闭合轨道”，或“循环”，是一个闭合轨迹的图像。极限环是一个循环，它是其他轨迹的极限集。

属性

通过若尔当曲线定理 Jordan Curve Theorem，每一个封闭的轨迹将平面分成两个区域，内部和外部的曲线。


给定一个极限环和它内部在时间上趋近[math]\displaystyle{ + \infty }[/math]的接近极限环的轨迹，在极限环周围有一个邻域，这样所有内部开始的轨迹在时间上趋近[math]\displaystyle{ + \infty }[/math]时都接近极限环。相应的陈述适用于时间上趋近[math]\displaystyle{ - \infty }[/math]的接近极限环的内部轨道，也适用于接近极限环的外部轨道。


稳定、不稳定和半稳定极限环

当所有相邻轨迹在时间趋于无穷大时都接近极限环时，称之为“稳定”或“吸引”极限环（ω- 极限环）。当时间趋近于负无穷时，若所有相邻轨线都逼近它，则它是一个不稳定的极限环（α- 极限环）。如果存在一个相邻轨迹，当时间趋于无穷大时螺旋进入极限环，另一个轨迹在时间趋于负无穷大时螺旋进入极限环，那么它是一个半稳定的极限环。还有一些既不稳定、不稳定也不半稳定的极限环 例如，邻近轨迹可能从外部接近极限环，但极限环的内部是由一组其他的极限环逼近的（不是极限环）。


稳定极限环是吸引子 Attractor的例子。它们意味着自我维持的振荡 Oscillation：闭合轨迹描述了系统的完美周期行为，任何来自这个闭合轨迹的微小扰动都会导致系统返回到它，使系统保持极限环。


寻找极限环

每一个闭合轨迹在其内部都包含一个系统的驻点 Stationary Point，即点[math]\displaystyle{ p }[/math]当有[math]\displaystyle{ V(p)=0 }[/math].本迪克森-杜拉克定理 Bendixson–Dulac theorem和庞加莱-本迪克森定理 Poincaré–Bendixson theorem 分别预言了二维非线性动力系统极限环的缺失或存在。


待解决的问题

一般来说，寻找极限环是一个非常困难的问题。平面上一个多项式微分方程的极限环的个数是希尔伯特第十六题 Hilbert's sixteenth problem第二部分的主要对象。例如，在平面上是否存在一个系统[math]\displaystyle{ x'=V(x) }[/math]，其中[math]\displaystyle{ V }[/math]的两个组成部分都是两个变量的二次多项式，这样的系统有多于4个极限环。


应用

霍普夫分岔 Hopf bifurcation附近不动点分支的极限环例子。红色的轨迹，深蓝色的稳定结构，浅蓝色的不稳定结构。参数的选择决定了极限环的出现和稳定性。

科学应用中许多自持振荡系统的仿真里，极限环具有重要意义。一些例子包括:

  • 空气动力学极限环振荡[1]
  • 神经元动作电位的霍奇金-赫胥黎模型 Hodgkin–Huxley model。
  • 糖酵解的塞尔科夫模型 Sel'kov model[2]。
  • 动物基因表达、激素水平和体温的日常变化，这些都是昼夜节律 circadian rhythm的一部分[3][4]。
  • 癌细胞在局限微环境中的迁移遵循极限环振荡[5] 。
  • 一些非线性电路表现出极限环振荡[6]，这启发了最初的范德波尔模型 Van der Pol model。

另见

参考文献

  1. ↑ Thomas, Jeffrey P.; Dowell, Earl H.; Hall, Kenneth C. (2002), "Nonlinear Inviscid Aerodynamic Effects on Transonic Divergence, Flutter, and Limit-Cycle Oscillations" (PDF), AIAA Journal, American Institute of Aeronautics and Astronautics, 40 (4): 638, Bibcode:2002AIAAJ..40..638T, doi:10.2514/2.1720, retrieved December 9, 2019
  2. ↑ Sel'kov, E. E. (1968). "Self-Oscillations in Glycolysis 1. A Simple Kinetic Model". European Journal of Biochemistry (in English). 4 (1): 79–86. doi:10.1111/j.1432-1033.1968.tb00175.x. ISSN 1432-1033. PMID 4230812.
  3. ↑ Leloup, Jean-Christophe; Gonze, Didier; Goldbeter, Albert (1999-12-01). "Limit Cycle Models for Circadian Rhythms Based on Transcriptional Regulation in Drosophila and Neurospora". Journal of Biological Rhythms (in English). 14 (6): 433–448. doi:10.1177/074873099129000948. ISSN 0748-7304. PMID 10643740.
  4. ↑ Roenneberg, Till; Chua, Elaine Jane; Bernardo, Ric; Mendoza, Eduardo (2008-09-09). "Modelling Biological Rhythms". Current Biology. 18 (17): R826–R835. doi:10.1016/j.cub.2008.07.017. ISSN 0960-9822. PMID 18786388.
  5. ↑ Brückner, David B.; Fink, Alexandra; Schreiber, Christoph; Röttgermann, Peter J. F.; Rädler, Joachim; Broedersz, Chase P. (2019). "Stochastic nonlinear dynamics of confined cell migration in two-state systems". Nature Physics (in English). 15 (6): 595–601. Bibcode:2019NatPh..15..595B. doi:10.1038/s41567-019-0445-4. ISSN 1745-2481.
  6. ↑ Ginoux, Jean-Marc; Letellier, Christophe (2012-04-30). "Van der Pol and the history of relaxation oscillations: Toward the emergence of a concept". Chaos: An Interdisciplinary Journal of Nonlinear Science. 22 (2): 023120. arXiv:1408.4890. Bibcode:2012Chaos..22b3120G. doi:10.1063/1.3670008. ISSN 1054-1500. PMID 22757527.


进一步阅读

  • Steven H. Strogatz (2014). Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering. Avalon. ISBN 9780813349114. 
  • M. Vidyasagar (2002). Nonlinear Systems Analysis (Second ed.). SIAM. ISBN 9780898715262. 
  • Philip Hartman, "Ordinary Differential Equation", Society for Industrial and Applied Mathematics, 2002.
  • Witold Hurewicz, "Lectures on Ordinary Differential Equations", Dover, 2002.
  • Solomon Lefschetz, "Differential Equations: Geometric Theory", Dover, 2005.
  • Lawrence Perko, "Differential Equations and Dynamical Systems", Springer-Verlag, 2006.


其他链接


编者推荐

集智文章推荐

什么是非线性系统 | 集智百科

描述变量随时间变化的非线性动力系统与较之简单得多的线性系统相比，可能显得混沌、不可预测或违反直觉。


取自“https://wiki.swarma.org/index.php?title=极限环&oldid=20797”