“条件熵”的版本间的差异
| 第1行: | 第1行: | ||
此词条由Jie翻译。由Lincent审校。 | 此词条由Jie翻译。由Lincent审校。 | ||
| − | |||
| − | |||
| − | |||
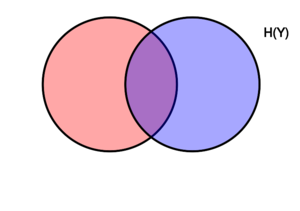
[[文件:Entropy-mutual-information-relative-entropy-relation-diagram.svg|缩略图|右|该图表示在变量X、Y相关联的各种信息量之间,进行加减关系的维恩图。两个圆所包含的区域是联合熵H(X,Y)。左侧的圆圈(红色和紫色)是单个熵H(X),红色是条件熵H(X ǀ Y)。右侧的圆圈(蓝色和紫色)为H(Y),蓝色为H(Y ǀ X)。中间紫色的是相互信息i(X; Y)。]] | [[文件:Entropy-mutual-information-relative-entropy-relation-diagram.svg|缩略图|右|该图表示在变量X、Y相关联的各种信息量之间,进行加减关系的维恩图。两个圆所包含的区域是联合熵H(X,Y)。左侧的圆圈(红色和紫色)是单个熵H(X),红色是条件熵H(X ǀ Y)。右侧的圆圈(蓝色和紫色)为H(Y),蓝色为H(Y ǀ X)。中间紫色的是相互信息i(X; Y)。]] | ||
| − | |||
| − | 在 | + | 在[[信息论 Information theory]]中,假设随机变量<math>X</math>的值已知,那么'''条件熵 Conditional entropy'''则用于定量描述随机变量<math>Y</math>表示的信息量。此时,信息以香农 Shannon''','''<font color="#ff8000">奈特 nat</font>'''或'''<font color="#ff8000">哈特莱 hartley</font>'''来衡量。已知<math>X</math>的条件下<math>Y</math>的熵记为<math>H(X ǀ Y)</math>。 |
| − | == | + | == 定义 == |
| − | |||
在给定<math>X</math>的情况下,<math>Y</math>的条件熵定义为: | 在给定<math>X</math>的情况下,<math>Y</math>的条件熵定义为: | ||
| − | |||
| 第28行: | 第22行: | ||
|background colour=#F5FFFA}} | |background colour=#F5FFFA}} | ||
| − | |||
| − | |||
| − | |||
其中<math>\mathcal X</math>和<math>\mathcal Y</math>表示<math>X</math>和<math>Y</math>的'''<font color="#ff8000">支撑集 support sets</font>'''。 | 其中<math>\mathcal X</math>和<math>\mathcal Y</math>表示<math>X</math>和<math>Y</math>的'''<font color="#ff8000">支撑集 support sets</font>'''。 | ||
| + | '''注意''':约定<math>c > 0</math>始终成立时,表达式<math>0 \log 0</math>和<math>0 \log c/0</math>视为等于零。这是因为<math>\lim_{\theta\to0^+} \theta\, \log \,c/\theta = 0</math>,而且<math>\lim_{\theta\to0^+} \theta\, \log \theta = 0</math>><ref>{{Cite web|url=http://www.inference.org.uk/mackay/itprnn/book.html|title=David MacKay: Information Theory, Pattern Recognition and Neural Networks: The Book|website=www.inference.org.uk|access-date=2019-10-25}}</ref> <!-- because p(x,y) could still equal 0 even if p(x) != 0 and p(y) != 0. What about p(x,y)=p(x)=0? --> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
对该定义的直观解释是:根据定义<math>\displaystyle H( Y|X) =\mathbb{E}( \ f( X,Y) \ )</math>,其中<math>\displaystyle f:( x,y) \ \rightarrow -\log( \ p( y|x) \ ) </math>. <math>\displaystyle f</math>将给定<math>\displaystyle (X=x)</math>时的<math>\displaystyle ( Y=y)</math>的信息内容与<math>\displaystyle ( x,y)</math>相关联,这是描述在给定<math>(X=x)</math>条件下的事件<math>\displaystyle (Y=y)</math>所需的信息量。根据大数定律,<math>H(Y ǀ X)</math>是大量<math>\displaystyle f(X,Y)</math>独立实验结果的算术平均值。 | 对该定义的直观解释是:根据定义<math>\displaystyle H( Y|X) =\mathbb{E}( \ f( X,Y) \ )</math>,其中<math>\displaystyle f:( x,y) \ \rightarrow -\log( \ p( y|x) \ ) </math>. <math>\displaystyle f</math>将给定<math>\displaystyle (X=x)</math>时的<math>\displaystyle ( Y=y)</math>的信息内容与<math>\displaystyle ( x,y)</math>相关联,这是描述在给定<math>(X=x)</math>条件下的事件<math>\displaystyle (Y=y)</math>所需的信息量。根据大数定律,<math>H(Y ǀ X)</math>是大量<math>\displaystyle f(X,Y)</math>独立实验结果的算术平均值。 | ||
| 第48行: | 第33行: | ||
| − | == | + | == 动机 == |
| − | |||
设<math>H(Y ǀ X = x)</math>为离散随机变量<math>Y</math>在离散随机变量<math>X</math>取定值<math>x</math>时的熵。用<math>\mathcal X</math>和<math>\mathcal Y</math>表示<math>X</math>和<math>Y</math>的支撑集。令<math>Y</math>的概率密度函数为<math>p_Y{(y)}</math>。<math>Y</math>的无条件熵计算为<math>H(Y):=E[I(Y)</math>。 | 设<math>H(Y ǀ X = x)</math>为离散随机变量<math>Y</math>在离散随机变量<math>X</math>取定值<math>x</math>时的熵。用<math>\mathcal X</math>和<math>\mathcal Y</math>表示<math>X</math>和<math>Y</math>的支撑集。令<math>Y</math>的概率密度函数为<math>p_Y{(y)}</math>。<math>Y</math>的无条件熵计算为<math>H(Y):=E[I(Y)</math>。 | ||
| 第57行: | 第41行: | ||
= -\sum_{y\in\mathcal Y} {p_Y(y) \log_2{p_Y(y)}},</math> | = -\sum_{y\in\mathcal Y} {p_Y(y) \log_2{p_Y(y)}},</math> | ||
| − | |||
| − | |||
当<math>Y</math>取值为<math>y_i</math>时,<math>\operatorname{I}(y_i)</math>是其结果<math>Y</math>的信息内容。类似地,当<math>X</math>值为<math>x</math>时以<math>X</math>为条件的<math>Y</math>的熵,也可以通过条件期望来定义: | 当<math>Y</math>取值为<math>y_i</math>时,<math>\operatorname{I}(y_i)</math>是其结果<math>Y</math>的信息内容。类似地,当<math>X</math>值为<math>x</math>时以<math>X</math>为条件的<math>Y</math>的熵,也可以通过条件期望来定义: | ||
| 第67行: | 第49行: | ||
| − | + | '''注意''',<math> H(Y ǀ X)</math>是在<math>X</math>可能取的所有可能值<math>x</math>时对<math>H(Y ǀ X = x)</math>求平均值的结果。同样,如果上述和取自样本<math>y_1, \dots, y_n</math>上,则期望值<math>E_X[ H(y_1, \dots, y_n \mid X = x)]</math><font color="#32cd32"> 在某些领域中认为是模糊值</font>。<ref>{{cite journal|author1=Hellman, M.|author2=Raviv, J.|year=1970|title=Probability of error, equivocation, and the Chernoff bound|journal=IEEE Transactions on Information Theory|volume=16|issue=4|pp=368-372}}</ref> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
给定具有像<math>\mathcal X</math>的离散随机变量<math>X</math>和具有像<math>\mathcal Y</math>的离散随机变量<math>Y</math>,将给定<math>X</math>的<math>Y</math>的条件熵定义为以<math>p(x)</math>作为权重,对<math>x</math>的每个可能取值得到的<math>H(Y|X=x)</math>的加权和。其表达式如下:<ref name=cover1991>{{cite book|isbn=0-471-06259-6|year=1991|authorlink1=Thomas M. Cover|author1=T. Cover|author2=J. Thomas|title=Elements of Information Theory|url=https://archive.org/details/elementsofinform0000cove|url-access=registration}}</ref>{{rp|15}} | 给定具有像<math>\mathcal X</math>的离散随机变量<math>X</math>和具有像<math>\mathcal Y</math>的离散随机变量<math>Y</math>,将给定<math>X</math>的<math>Y</math>的条件熵定义为以<math>p(x)</math>作为权重,对<math>x</math>的每个可能取值得到的<math>H(Y|X=x)</math>的加权和。其表达式如下:<ref name=cover1991>{{cite book|isbn=0-471-06259-6|year=1991|authorlink1=Thomas M. Cover|author1=T. Cover|author2=J. Thomas|title=Elements of Information Theory|url=https://archive.org/details/elementsofinform0000cove|url-access=registration}}</ref>{{rp|15}} | ||
| 第89行: | 第66行: | ||
</math> | </math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | == 属性 == | ||
| + | === 条件熵等于零 Conditional entropy equals zero === | ||
当且仅当<math>Y</math>的值完全由<math>X</math>的值确定时,<math>H(Y|X)=0</math>。 | 当且仅当<math>Y</math>的值完全由<math>X</math>的值确定时,<math>H(Y|X)=0</math>。 | ||
| − | + | ===独立随机变量的条件熵 Conditional entropy of independent random variables === | |
| − | === Conditional entropy of independent random variables | ||
| − | |||
相反,当且仅当<math>Y</math>和<math>X</math>是互相独立的随机变量时,则<math>H(Y|X) =H(Y)</math>。 | 相反,当且仅当<math>Y</math>和<math>X</math>是互相独立的随机变量时,则<math>H(Y|X) =H(Y)</math>。 | ||
| 第108行: | 第78行: | ||
| − | === Chain rule | + | === 链式法则 Chain rule === |
| − | + | 假设由两个随机变量<math>X</math>和<math>Y</math>确定的组合系统具有[[联合熵]]<math>H(X,Y)</math>,也就是说,我们通常需要<math>H(X,Y)</math>位信息来描述其确切状态。现在,如果我们首先尝试获得<math>X</math>的值,我们将知晓<math>H(X)</math>位信息。一旦<math>X</math>的值确定,我们就可以通过<math>H(X,Y)</math>-<math>H(X)</math>位来描述整个系统的状态。这个数量恰好是<math>H(Y|X)</math>,它给出了条件熵的链式法则: | |
| − | |||
| − | |||
:<math>H(Y|X)\, = \, H(X,Y)- H(X).</math><ref name=cover1991 />{{rp|17}} | :<math>H(Y|X)\, = \, H(X,Y)- H(X).</math><ref name=cover1991 />{{rp|17}} | ||
| − | |||
| − | |||
链式法则遵循以上条件熵的定义: | 链式法则遵循以上条件熵的定义: | ||
| 第130行: | 第96行: | ||
\end{align}</math> | \end{align}</math> | ||
| − | |||
| − | |||
通常情况下,多个随机变量的链式法则表示为: | 通常情况下,多个随机变量的链式法则表示为: | ||
| 第139行: | 第103行: | ||
\sum_{i=1}^n H(X_i | X_1, \ldots, X_{i-1}) </math><ref name=cover1991 />{{rp|22}} | \sum_{i=1}^n H(X_i | X_1, \ldots, X_{i-1}) </math><ref name=cover1991 />{{rp|22}} | ||
| − | |||
| − | |||
除了使用加法而不是乘法之外,它具有与概率论中的链式法则类似的形式。 | 除了使用加法而不是乘法之外,它具有与概率论中的链式法则类似的形式。 | ||
| 第146行: | 第108行: | ||
| − | === Bayes' rule | + | ===贝叶斯法则 Bayes' rule === |
| − | [[Bayes' rule]] | + | 条件熵状态的[[贝叶斯法则 Bayes' rule]] |
| − | |||
| − | |||
| 第155行: | 第115行: | ||
| − | '' | + | '''证明''',<math>H(Y|X) = H(X,Y) - H(X)</math> 和 <math>H(X|Y) = H(Y,X) - H(Y)</math>。对称性要求<math>H(X,Y) = H(Y,X)</math>。将两个方程式相减就意味着贝叶斯定律。 |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
如果给定<math>X</math>,<math>Y</math>有条件地独立于<math>Z</math>,则有: | 如果给定<math>X</math>,<math>Y</math>有条件地独立于<math>Z</math>,则有: | ||
| 第169行: | 第124行: | ||
| − | + | ===其他性质 === | |
| − | === | ||
| − | |||
| − | |||
对于任何<math>X</math>和<math>Y</math>: | 对于任何<math>X</math>和<math>Y</math>: | ||
| 第183行: | 第135行: | ||
\end{align}</math> | \end{align}</math> | ||
| − | |||
| − | 其中<math>\operatorname{I}(X;Y)</math>是<math>X</math>和<math>Y</math>之间的 | + | 其中<math>\operatorname{I}(X;Y)</math>是<math>X</math>和<math>Y</math>之间的[[互信息 mutual information]]。 |
| − | + | 对于独立的<math>X</math>和<math>Y</math>: | |
| − | |||
| − | |||
| − | |||
:<math>H(Y|X) = H(Y) </math> and <math>H(X|Y) = H(X) \, </math> | :<math>H(Y|X) = H(Y) </math> and <math>H(X|Y) = H(X) \, </math> | ||
| − | |||
| − | |||
对于给定随机变量<math>Y</math>的值<math>y</math>,尽管特定条件熵<math>H(X|Y=y)</math>可以小于或大于<math>H(X)</math>,但<math>H(X|Y)</math>永远不会超过<math>H(X)</math>。 | 对于给定随机变量<math>Y</math>的值<math>y</math>,尽管特定条件熵<math>H(X|Y=y)</math>可以小于或大于<math>H(X)</math>,但<math>H(X|Y)</math>永远不会超过<math>H(X)</math>。 | ||
| 第203行: | 第149行: | ||
| − | == Conditional differential entropy | + | == 条件微分熵 Conditional differential entropy == |
| − | === | + | === 定义 === |
| − | |||
| − | |||
上面的定义是针对离散随机变量的。离散条件熵的连续形式称为'''<font color="#ff8000">条件微分(或连续)熵 Conditional differential (or continuous) entropy </font>'''。 令<math>X</math>和<math>Y</math>为具有联合概率密度函数<math>f(x,y)</math>的连续随机变量。则微分条件熵<math>h(X|Y)</math>定义为:<ref name=cover1991 />{{rp|249}} | 上面的定义是针对离散随机变量的。离散条件熵的连续形式称为'''<font color="#ff8000">条件微分(或连续)熵 Conditional differential (or continuous) entropy </font>'''。 令<math>X</math>和<math>Y</math>为具有联合概率密度函数<math>f(x,y)</math>的连续随机变量。则微分条件熵<math>h(X|Y)</math>定义为:<ref name=cover1991 />{{rp|249}} | ||
| 第220行: | 第164行: | ||
| − | === Properties | + | ===属性 Properties === |
| − | |||
| − | |||
与离散随机变量的条件熵相比,条件微分熵可能为负。 | 与离散随机变量的条件熵相比,条件微分熵可能为负。 | ||
| − | |||
| − | |||
| − | |||
与离散情况一样,微分熵也有链式法则: | 与离散情况一样,微分熵也有链式法则: | ||
| 第234行: | 第173行: | ||
:<math>h(Y|X)\,=\,h(X,Y)-h(X)</math><ref name=cover1991 />{{rp|253}} | :<math>h(Y|X)\,=\,h(X,Y)-h(X)</math><ref name=cover1991 />{{rp|253}} | ||
| − | |||
| − | |||
但是请注意,如果所涉及的微分熵不存在或无限,则此法则可能不成立。 | 但是请注意,如果所涉及的微分熵不存在或无限,则此法则可能不成立。 | ||
| 第241行: | 第178行: | ||
| − | Joint differential | + | 联合微分熵 Joint differential entropy也用于定义连续随机变量之间的互信息: |
| − | |||
| − | |||
| 第249行: | 第184行: | ||
| − | <math> | + | 当且仅当<math>X</math>和<math>Y</math>是独立的,<math>h(X|Y) \le h(X)</math>等号成立。<ref name=cover1991 />{{rp|253}} |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | === 与估计量误差的关系Relation to estimator error === | ||
条件微分熵在估计量的期望平方误差上有一个下限。对于任何随机变量<math>X</math>,观察值<math>Y</math>和估计量<math>\widehat{X}</math>,以下条件成立: | 条件微分熵在估计量的期望平方误差上有一个下限。对于任何随机变量<math>X</math>,观察值<math>Y</math>和估计量<math>\widehat{X}</math>,以下条件成立: | ||
| 第265行: | 第196行: | ||
| − | + | 这与来自[[量子力学 quantum mechanics]]的[[不确定性原理 uncertainty principle]]有关。 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | + | == 量子理论泛化 Generalization to quantum theory == |
| − | + | 在[[量子信息论 quantum information theory]]中,条件熵被广义化为条件量子熵。后者可以采用负值,这与经典方法不同。 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | == 另见 == | ||
| + | * [[熵(信息论) Entropy (information theory)]] | ||
| + | * [[互信息 Mutual information]] | ||
| + | * [[条件量子熵 Conditional quantum entropy]] | ||
| + | * [[信息差异 Variation of information]] | ||
| + | * [[熵幂不等式 Entropy power inequality]] | ||
| + | * [[似然函数 Likelihood function]] | ||
| 第298行: | 第216行: | ||
{{Reflist}} | {{Reflist}} | ||
| − | [[Category: | + | [[Category:熵和信息]] |
| − | [[Category: | + | [[Category:信息理论]] |
2021年1月17日 (日) 21:49的版本
此词条由Jie翻译。由Lincent审校。
在信息论 Information theory中,假设随机变量[math]\displaystyle{ X }[/math]的值已知,那么条件熵 Conditional entropy则用于定量描述随机变量[math]\displaystyle{ Y }[/math]表示的信息量。此时,信息以香农 Shannon,奈特 nat或哈特莱 hartley来衡量。已知[math]\displaystyle{ X }[/math]的条件下[math]\displaystyle{ Y }[/math]的熵记为[math]\displaystyle{ H(X ǀ Y) }[/math]。
定义
在给定[math]\displaystyle{ X }[/math]的情况下,[math]\displaystyle{ Y }[/math]的条件熵定义为:
[math]\displaystyle{ \Eta(Y|X)\ = -\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log \frac {p(x,y)} {p(x)} }[/math]
|
|
(Eq.1) |
其中[math]\displaystyle{ \mathcal X }[/math]和[math]\displaystyle{ \mathcal Y }[/math]表示[math]\displaystyle{ X }[/math]和[math]\displaystyle{ Y }[/math]的支撑集 support sets。
注意:约定[math]\displaystyle{ c \gt 0 }[/math]始终成立时,表达式[math]\displaystyle{ 0 \log 0 }[/math]和[math]\displaystyle{ 0 \log c/0 }[/math]视为等于零。这是因为[math]\displaystyle{ \lim_{\theta\to0^+} \theta\, \log \,c/\theta = 0 }[/math],而且[math]\displaystyle{ \lim_{\theta\to0^+} \theta\, \log \theta = 0 }[/math]>[1]
对该定义的直观解释是:根据定义[math]\displaystyle{ \displaystyle H( Y|X) =\mathbb{E}( \ f( X,Y) \ ) }[/math],其中[math]\displaystyle{ \displaystyle f:( x,y) \ \rightarrow -\log( \ p( y|x) \ ) }[/math]. [math]\displaystyle{ \displaystyle f }[/math]将给定[math]\displaystyle{ \displaystyle (X=x) }[/math]时的[math]\displaystyle{ \displaystyle ( Y=y) }[/math]的信息内容与[math]\displaystyle{ \displaystyle ( x,y) }[/math]相关联,这是描述在给定[math]\displaystyle{ (X=x) }[/math]条件下的事件[math]\displaystyle{ \displaystyle (Y=y) }[/math]所需的信息量。根据大数定律,[math]\displaystyle{ H(Y ǀ X) }[/math]是大量[math]\displaystyle{ \displaystyle f(X,Y) }[/math]独立实验结果的算术平均值。
动机
设[math]\displaystyle{ H(Y ǀ X = x) }[/math]为离散随机变量[math]\displaystyle{ Y }[/math]在离散随机变量[math]\displaystyle{ X }[/math]取定值[math]\displaystyle{ x }[/math]时的熵。用[math]\displaystyle{ \mathcal X }[/math]和[math]\displaystyle{ \mathcal Y }[/math]表示[math]\displaystyle{ X }[/math]和[math]\displaystyle{ Y }[/math]的支撑集。令[math]\displaystyle{ Y }[/math]的概率密度函数为[math]\displaystyle{ p_Y{(y)} }[/math]。[math]\displaystyle{ Y }[/math]的无条件熵计算为[math]\displaystyle{ H(Y):=E[I(Y) }[/math]。
- [math]\displaystyle{ H(Y) = \sum_{y\in\mathcal Y} {\mathrm{Pr}(Y=y)\,\mathrm{I}(y)} = -\sum_{y\in\mathcal Y} {p_Y(y) \log_2{p_Y(y)}}, }[/math]
当[math]\displaystyle{ Y }[/math]取值为[math]\displaystyle{ y_i }[/math]时,[math]\displaystyle{ \operatorname{I}(y_i) }[/math]是其结果[math]\displaystyle{ Y }[/math]的信息内容。类似地,当[math]\displaystyle{ X }[/math]值为[math]\displaystyle{ x }[/math]时以[math]\displaystyle{ X }[/math]为条件的[math]\displaystyle{ Y }[/math]的熵,也可以通过条件期望来定义:
- [math]\displaystyle{ H(Y|X=x) = -\sum_{y\in\mathcal Y} {\Pr(Y = y|X=x) \log_2{\Pr(Y = y|X=x)}}. }[/math]
注意,[math]\displaystyle{ H(Y ǀ X) }[/math]是在[math]\displaystyle{ X }[/math]可能取的所有可能值[math]\displaystyle{ x }[/math]时对[math]\displaystyle{ H(Y ǀ X = x) }[/math]求平均值的结果。同样,如果上述和取自样本[math]\displaystyle{ y_1, \dots, y_n }[/math]上,则期望值[math]\displaystyle{ E_X[ H(y_1, \dots, y_n \mid X = x)] }[/math] 在某些领域中认为是模糊值。[2]
给定具有像[math]\displaystyle{ \mathcal X }[/math]的离散随机变量[math]\displaystyle{ X }[/math]和具有像[math]\displaystyle{ \mathcal Y }[/math]的离散随机变量[math]\displaystyle{ Y }[/math],将给定[math]\displaystyle{ X }[/math]的[math]\displaystyle{ Y }[/math]的条件熵定义为以[math]\displaystyle{ p(x) }[/math]作为权重,对[math]\displaystyle{ x }[/math]的每个可能取值得到的[math]\displaystyle{ H(Y|X=x) }[/math]的加权和。其表达式如下:[3]:15
- [math]\displaystyle{ \begin{align} H(Y|X)\ &\equiv \sum_{x\in\mathcal X}\,p(x)\,H(Y|X=x)\\ & =-\sum_{x\in\mathcal X} p(x)\sum_{y\in\mathcal Y}\,p(y|x)\,\log\, p(y|x)\\ & =-\sum_{x\in\mathcal X}\sum_{y\in\mathcal Y}\,p(x,y)\,\log\,p(y|x)\\ & =-\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log\,p(y|x)\\ & =-\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log \frac {p(x,y)} {p(x)}. \\ & = \sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log \frac {p(x)} {p(x,y)}. \\ \end{align} }[/math]
属性
条件熵等于零 Conditional entropy equals zero
当且仅当[math]\displaystyle{ Y }[/math]的值完全由[math]\displaystyle{ X }[/math]的值确定时,[math]\displaystyle{ H(Y|X)=0 }[/math]。
独立随机变量的条件熵 Conditional entropy of independent random variables
相反,当且仅当[math]\displaystyle{ Y }[/math]和[math]\displaystyle{ X }[/math]是互相独立的随机变量时,则[math]\displaystyle{ H(Y|X) =H(Y) }[/math]。
链式法则 Chain rule
假设由两个随机变量[math]\displaystyle{ X }[/math]和[math]\displaystyle{ Y }[/math]确定的组合系统具有联合熵[math]\displaystyle{ H(X,Y) }[/math],也就是说,我们通常需要[math]\displaystyle{ H(X,Y) }[/math]位信息来描述其确切状态。现在,如果我们首先尝试获得[math]\displaystyle{ X }[/math]的值,我们将知晓[math]\displaystyle{ H(X) }[/math]位信息。一旦[math]\displaystyle{ X }[/math]的值确定,我们就可以通过[math]\displaystyle{ H(X,Y) }[/math]-[math]\displaystyle{ H(X) }[/math]位来描述整个系统的状态。这个数量恰好是[math]\displaystyle{ H(Y|X) }[/math],它给出了条件熵的链式法则:
- [math]\displaystyle{ H(Y|X)\, = \, H(X,Y)- H(X). }[/math][3]:17
链式法则遵循以上条件熵的定义:
- [math]\displaystyle{ \begin{align} H(Y|X) &= \sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log \left(\frac{p(x)}{p(x,y)} \right) \\[4pt] &= \sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)(\log (p(x))-\log (p(x,y))) \\[4pt] &= -\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log (p(x,y)) + \sum_{x\in\mathcal X, y\in\mathcal Y}{p(x,y)\log(p(x))} \\[4pt] & = H(X,Y) + \sum_{x \in \mathcal X} p(x)\log (p(x) ) \\[4pt] & = H(X,Y) - H(X). \end{align} }[/math]
通常情况下,多个随机变量的链式法则表示为:
- [math]\displaystyle{ H(X_1,X_2,\ldots,X_n) = \sum_{i=1}^n H(X_i | X_1, \ldots, X_{i-1}) }[/math][3]:22
除了使用加法而不是乘法之外,它具有与概率论中的链式法则类似的形式。
贝叶斯法则 Bayes' rule
条件熵状态的贝叶斯法则 Bayes' rule
- [math]\displaystyle{ H(Y|X) \,=\, H(X|Y) - H(X) + H(Y). }[/math]
证明,[math]\displaystyle{ H(Y|X) = H(X,Y) - H(X) }[/math] 和 [math]\displaystyle{ H(X|Y) = H(Y,X) - H(Y) }[/math]。对称性要求[math]\displaystyle{ H(X,Y) = H(Y,X) }[/math]。将两个方程式相减就意味着贝叶斯定律。
如果给定[math]\displaystyle{ X }[/math],[math]\displaystyle{ Y }[/math]有条件地独立于[math]\displaystyle{ Z }[/math],则有:
- [math]\displaystyle{ H(Y|X,Z) \,=\, H(Y|X). }[/math]
其他性质
对于任何[math]\displaystyle{ X }[/math]和[math]\displaystyle{ Y }[/math]:
- [math]\displaystyle{ \begin{align} H(Y|X) &\le H(Y) \, \\ H(X,Y) &= H(X|Y) + H(Y|X) + \operatorname{I}(X;Y),\qquad \\ H(X,Y) &= H(X) + H(Y) - \operatorname{I}(X;Y),\, \\ \operatorname{I}(X;Y) &\le H(X),\, \end{align} }[/math]
其中[math]\displaystyle{ \operatorname{I}(X;Y) }[/math]是[math]\displaystyle{ X }[/math]和[math]\displaystyle{ Y }[/math]之间的互信息 mutual information。
对于独立的[math]\displaystyle{ X }[/math]和[math]\displaystyle{ Y }[/math]:
- [math]\displaystyle{ H(Y|X) = H(Y) }[/math] and [math]\displaystyle{ H(X|Y) = H(X) \, }[/math]
对于给定随机变量[math]\displaystyle{ Y }[/math]的值[math]\displaystyle{ y }[/math],尽管特定条件熵[math]\displaystyle{ H(X|Y=y) }[/math]可以小于或大于[math]\displaystyle{ H(X) }[/math],但[math]\displaystyle{ H(X|Y) }[/math]永远不会超过[math]\displaystyle{ H(X) }[/math]。
条件微分熵 Conditional differential entropy
定义
上面的定义是针对离散随机变量的。离散条件熵的连续形式称为条件微分(或连续)熵 Conditional differential (or continuous) entropy 。 令[math]\displaystyle{ X }[/math]和[math]\displaystyle{ Y }[/math]为具有联合概率密度函数[math]\displaystyle{ f(x,y) }[/math]的连续随机变量。则微分条件熵[math]\displaystyle{ h(X|Y) }[/math]定义为:[3]:249
[math]\displaystyle{ h(X|Y) = -\int_{\mathcal X, \mathcal Y} f(x,y)\log f(x|y)\,dx dy }[/math]
|
|
(Eq.2) |
属性 Properties
与离散随机变量的条件熵相比,条件微分熵可能为负。
与离散情况一样,微分熵也有链式法则:
- [math]\displaystyle{ h(Y|X)\,=\,h(X,Y)-h(X) }[/math][3]:253
但是请注意,如果所涉及的微分熵不存在或无限,则此法则可能不成立。
联合微分熵 Joint differential entropy也用于定义连续随机变量之间的互信息:
- [math]\displaystyle{ \operatorname{I}(X,Y)=h(X)-h(X|Y)=h(Y)-h(Y|X) }[/math]
当且仅当[math]\displaystyle{ X }[/math]和[math]\displaystyle{ Y }[/math]是独立的,[math]\displaystyle{ h(X|Y) \le h(X) }[/math]等号成立。[3]:253
与估计量误差的关系Relation to estimator error
条件微分熵在估计量的期望平方误差上有一个下限。对于任何随机变量[math]\displaystyle{ X }[/math],观察值[math]\displaystyle{ Y }[/math]和估计量[math]\displaystyle{ \widehat{X} }[/math],以下条件成立:
- [math]\displaystyle{ \mathbb{E}\left[\bigl(X - \widehat{X}{(Y)}\bigr)^2\right] \ge \frac{1}{2\pi e}e^{2h(X|Y)} }[/math]
这与来自量子力学 quantum mechanics的不确定性原理 uncertainty principle有关。
量子理论泛化 Generalization to quantum theory
在量子信息论 quantum information theory中,条件熵被广义化为条件量子熵。后者可以采用负值,这与经典方法不同。
另见
- 熵(信息论) Entropy (information theory)
- 互信息 Mutual information
- 条件量子熵 Conditional quantum entropy
- 信息差异 Variation of information
- 熵幂不等式 Entropy power inequality
- 似然函数 Likelihood function
References 参考文献
- ↑ "David MacKay: Information Theory, Pattern Recognition and Neural Networks: The Book". www.inference.org.uk. Retrieved 2019-10-25.
- ↑ Hellman, M.; Raviv, J. (1970). "Probability of error, equivocation, and the Chernoff bound". IEEE Transactions on Information Theory. 16 (4): 368–372.
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 T. Cover; J. Thomas (1991). Elements of Information Theory. ISBN 0-471-06259-6. https://archive.org/details/elementsofinform0000cove.