“邻接表”的版本间的差异
(→参见) |
(→操作) |
||
| 第33行: | 第33行: | ||
==操作== | ==操作== | ||
| − | + | 邻接表数据结构执行的主要操作是列出给定顶点的邻居列表。使用上面详细说明的任何一种表示方式,都可以在每个邻居的固定时间内执行。换句话说,列出一个顶点 <math>''v'' </math>所有邻居的总时间与 <math>''v'' </math>的'''[[度]] Degree '''成正比。 | |
| − | + | 也可以使用邻接表来测试两个指定顶点之间是否存在边,但效率不高。在一个邻接表中,每个顶点的邻域都是不排序的,通过对该顶点的邻域进行'''<font color="#ff8000">顺序搜索 sequential search</font>''',可以按照给定两个顶点的最小阶数按时间比例进行边的存在性测试。如果邻域被表示为一个排序数组,则可以使用'''<font color="#ff8000">二分搜索法 binary search</font>''',时间与次数的对数成正比。 | |
<br> | <br> | ||
| + | |||
==权衡== | ==权衡== | ||
2021年1月20日 (三) 20:30的版本
在图论和计算机科学中,邻接表 Adjacency List是用来表示有限图 的无序表的集合。每个列表描述图中一个顶点的邻域集。这是计算机程序中常用的几种图形表示法之一。
实现
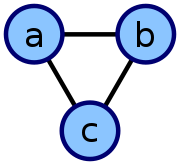
| 上图中的图表有这样的邻接表示法: | ||
| a | 毗邻 | b,c |
| b | 毗邻 | a,c |
| c | 毗邻 | a,b |
图的邻接表表示法将图中的每个顶点与其邻接顶点或边的集合关联起来。这个基本思想有许多变体,在如何实现顶点和集合之间的关联,如何实现集合,以及是否包括顶点和边还是只包括顶点作为第一类对象,以及什么类型的对象被用来表示顶点和边的细节上都有所不同。
- Guido van Rossum建议的实现方式是使用哈希表 hash table将图中的每个顶点与相邻顶点的数组数据结构联系起来。在这种表示方式中,一个顶点可以由任何可哈希的对象表示,没有明确地将边表示为对象。[1]。
- Cormen等人提出了一种用索引号来表示顶点的实现方法。[2]他们的表示方法是使用一个按顶点数索引的数组,其中每个顶点的数组单元格指向该顶点的相邻顶点的单链表 singly linked list。在这种表示方式中,单链表的节点可以解释为边对象;然而,它们并不存储关于每条边的完整信息(它们只存储边的两个端点中的一个) ,在无向图 Undirected Graph 中,每条边有两个不同的链表节点(边的两个端点中的每个端点的列表中都有一个)。
- Goodrich和Tamassia提出的面向对象入射列表结构有特殊的顶点对象和边缘对象类。每个顶点对象都有一个实例变量,指向一个集合对象,该集合对象列出了邻近的边缘对象。反过来,每个边缘对象又指向其端点的两个顶点对象。[3] 这种表示方式邻接表比直接列出相邻顶点的版本使用更多的内存,但是显示边对象的存在操作可以允许它在存储额外的关于边的信息方面有额外的灵活性。
操作
邻接表数据结构执行的主要操作是列出给定顶点的邻居列表。使用上面详细说明的任何一种表示方式,都可以在每个邻居的固定时间内执行。换句话说,列出一个顶点 [math]\displaystyle{ ''v'' }[/math]所有邻居的总时间与 [math]\displaystyle{ ''v'' }[/math]的度 Degree 成正比。
也可以使用邻接表来测试两个指定顶点之间是否存在边,但效率不高。在一个邻接表中,每个顶点的邻域都是不排序的,通过对该顶点的邻域进行顺序搜索 sequential search,可以按照给定两个顶点的最小阶数按时间比例进行边的存在性测试。如果邻域被表示为一个排序数组,则可以使用二分搜索法 binary search,时间与次数的对数成正比。
权衡
邻接表的主要替代方法是邻接矩阵 Adjacency Matrix,该矩阵的行和列按顶点索引,其单元格包含一个布尔值,该值指示与单元格的行和列对应的顶点之间是否存在边。对于稀疏图 Sparse Graph (大多数顶点对不是由边连接的图),邻接表比邻接矩阵(存储为二维数组)更节省空间:邻接表的空间使用与图中的边和顶点的数量成正比,而对于以这种方式存储的邻接矩阵,其空间与顶点数的平方成正比。然而,通过使用由顶点对索引的哈希表而不是数组,可以更有效地存储邻接矩阵的空间,从而匹配邻接表的线性空间使用。
邻接表和邻接矩阵之间的另一个显著区别是它们执行操作的效率。在邻接表中,每个顶点的邻居可以有效地列出,在时间上与顶点的程度成正比。在邻接矩阵中,这个操作需要的时间与图中顶点的数量成正比,而顶点的数量可能明显高于度。此外,邻接矩阵允许测试两个顶点是否在固定的时间内彼此相邻;邻接表支持这一操作的速度较慢。
数据结构
作为一种数据结构,邻接表的主要替代是邻接矩阵。因为邻接矩阵中的每个项只需要一个位,它可以用一种非常紧凑的方式表示,只占用[math]\displaystyle{ |V|^{2}/8 }[/math]字节的连续空间,其中[math]\displaystyle{ |V| }[/math]是图的顶点数。除了避免浪费空间之外,这种紧凑性还支持局部引用 locality of reference。
用稀疏邻接矩阵表示邻接表时,将占用更少的空间。这是因为它能避免为不存在的边分配任何空间。在一台32位计算机上,如果使用原始的数组结构实现邻接表,那么对于一个无向图来说,它大约需要占用[math]\displaystyle{ 2·(32/8)|E|= 8 |E| }[/math]字节的存储空间,其中[math]\displaystyle{ |E| }[/math]表示边的个数。每条边都将会在两个邻接表中重复出现,并分别占用4字节空间。
注意到一个无向简单图最多可以有[math]\displaystyle{ (|V|^{2}-|V|)/2≈ V^{2} }[/math]条边(允许循环),我们可以让[math]\displaystyle{ d = |E|/|V|^{2} }[/math]表示该图的密度。然后,当[math]\displaystyle{ 8|E| \gt |V|^{2}/8 }[/math]时,[math]\displaystyle{ |E|/|V|^{2} \gt 1/64 }[/math],即[math]\displaystyle{ d = |E|/|V|^{2}\gt 1/64 }[/math] ,邻接表表示比邻接矩阵表示占用更多的空间。因此,图必须足够稀疏,才适合使用邻接表表示。
除了空间上的权衡,不同的数据结构也有着不同的操作。在邻接表中找到与给定顶点相邻的所有顶点就像读取邻接表一样简单。对于邻接矩阵,必须扫描整行,这需要花费[math]\displaystyle{ O(|V|) }[/math]的时间。给定的两个顶点之间是否有边可以用邻接矩阵一次确定,并且运行时间与邻接列表中两个顶点的最小度数成正比。
参考资料
- ↑ Guido van Rossum (1998). "Python Patterns - Implementing Graphs".
- ↑ Thomas H. Cormen; Charles E. Leiserson; Ronald L. Rivest; Clifford Stein (2001). Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill.
- ↑ Michael T. Goodrich and Roberto Tamassia (2002). Algorithm Design: Foundations, Analysis, and Internet Examples. John Wiley & Sons. ISBN 0-471-38365-1.
延伸阅读
- David Eppstein (1996). "ICS 161 Lecture Notes: Graph Algorithms".
参见
- The Boost Graph Library implements an efficient adjacency list
编者推荐
书籍领读:图论
本课程中,将讲解巴拉巴西网络科学书籍第一章图论。
漫谈图论的起源、发展与应用
本课程中,介绍了图论中的基本概念和网络科学使用的工具,可以帮助认识真实网络的关键性质。
本中文词条由923397935参与编译,黄秋莉审校,Banditwen、薄荷编辑,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。