“多稳态”的版本间的差异
(→数学建模) |
|||
| 第1行: | 第1行: | ||
| + | {{#seo: | ||
| + | |keywords=多稳态,统计物理,双稳态 | ||
| + | |description=ISING模型 | ||
| + | }} | ||
| + | |||
| + | |||
在[[动力系统]]中,多稳态是系统中的一种状态属性,即由该系统的状态所形成的向量空间中,存在多个稳定平衡点。根据数学上的必然性,在稳定点之间也一定存在不稳定的平衡点。 | 在[[动力系统]]中,多稳态是系统中的一种状态属性,即由该系统的状态所形成的向量空间中,存在多个稳定平衡点。根据数学上的必然性,在稳定点之间也一定存在不稳定的平衡点。 | ||
| 第49行: | 第55行: | ||
<references /> | <references /> | ||
| + | ---- | ||
| + | 本中文词条由[[用户:舒寒|舒寒]]参与编译,[[用户:思无涯咿呀咿呀|思无涯咿呀咿呀]]编辑,欢迎在讨论页面留言。 | ||
| − | + | '''本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。''' | |
| − | + | [[category:复杂系统]] | |
| − | |||
| − | |||
2021年2月20日 (六) 16:46的版本
在动力系统中,多稳态是系统中的一种状态属性,即由该系统的状态所形成的向量空间中,存在多个稳定平衡点。根据数学上的必然性,在稳定点之间也一定存在不稳定的平衡点。
与L1、L2、L3前拉格朗日点一样,在某些维度上稳定而在其他维度上不稳定的点被称为不稳定点。
双稳态
双稳态是具有两个稳定平衡点的特殊情形。这是多重稳定性的最简单形式,可以发生在只有一个状态变量的系统中,因为它只需要一个一维空间来分隔两个点。[1]
在势能方面,一个双稳态系统有两个局部势能极小值,它们之间有一个局部极大值。一个双稳态的机械设备的例子是灯的开关,开关要么“开”要么“关”,但不会在二者之间停留。 在保守力场中,双稳态基于势能有三个平衡点的事实,其中两个极小,一个极大。通过数学讨论可知,极大值一定在两个极小值之间。一个处于基态的粒子位于两个平衡点中的一个,因为这对应着能量最小值。最大值可以被看作它们之间的一道屏障。
如果一个系统获得足够的活化能来穿过屏障(在化学例子中对比活化能与阿伦尼乌斯公式),那么它就可以从一个能量最小态过渡到另一个能量最小态。达到界限后,系统会在松弛时间后进入另一个能量最小态。
双稳态在数字电子设备中被广泛用于存储二进制数据。一个双稳态设备以一种状态代表“0”,另一种状态代表“1”的形式储存1比特的二进制数据。它同样被应用于张弛振荡器、多谐振荡器及施密特触发器。视觉双稳态是一些特定的视觉设备的分布,根据输入,这些设备中有两个稳定的共振的传送状态。双稳态也可以出现在生物化学系统中,它从持续的化学浓度和化学反应中产生数字式、开关式的输出。在这些系统中双稳态通常与滞后现象有关。
数学建模
在动态系统分析的数学语言中,最简单的双稳态系统之一是: [math]\displaystyle{ \frac{dy}{dt}=y\left(1-y^2\right) }[/math]
[math]\displaystyle{ \frac{y^4}{4}-\frac{y^2}{2} }[/math]
这个系统描述了一个沿着曲线[math]\displaystyle{ \frac{y^4}{4}-\frac{y^2}{2} }[/math]下滑的球,有三个定态:[math]\displaystyle{ y=1 }[/math],[math]\displaystyle{ y=0 }[/math],[math]\displaystyle{ y=-1 }[/math]和中间的定态是不稳定的,其它两个是稳定的。[math]\displaystyle{ y(t) }[/math]随时间变化的方向取决于初始条件[math]\displaystyle{ y(0) }[/math]。如果初始条件是正的,那么解y(t)随时间变化趋于1;但如果初始条件是负的,那么解[math]\displaystyle{ y(t) }[/math]随时间变化趋于-1。因此,这个动力系统是“双稳态”的。根据初值的不同,终态即可能是[math]\displaystyle{ y=1 }[/math]也可能是[math]\displaystyle{ y=-1 }[/math]。
可以通过[math]\displaystyle{ 系统=y(r-y) }[/math]来理解双稳态区域的表型,这个系统经历了一个分岔系数是[math]\displaystyle{ r }[/math]的超临界叉式分岔。
初始不稳定性
在不稳定平衡点附近,任何系统对噪声、初始条件和系统参数都很敏感,这肯能会导致它向多个不同的方向发展。
在经济学和社会科学中,路径依赖导致了发展方向上的分歧。一些路径的依赖过程可以通过多稳态来充分描述:在到达稳态之前,对输入的初始状态很敏感,比如最初市场份额不稳定,随后可能会演变成多个可能的供应商之一的稳定垄断。
多稳态知觉
多稳态知觉是一种较少见的视知觉现象。多稳态知觉常被描述为在观看一图形时,会主观性的观察到图形无法预期的自发性改变,并且这改变会接续不断发生。
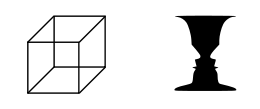
当一个图形对人类的视觉系统来说,是具有歧义性时,就会引发多稳态知觉的现象。如一些知名的例子如奈克方块Necker cube、运动中探知结构(structure from motion)、单眼竞争(monocular rivalry)和双眼竞争binocular rivalry。但更为人所知的是暧昧图形(ambiguous image)。因为这些图形通常会在两种知觉状态之间相互交换,所以又称为双稳态知觉。通过横向抑制,其中一个图像在受到刺激时会抑制邻近图像的活动。[2]
外部链接
参考文献
- ↑ https://baike.baidu.com/item/%E5%8F%8C%E7%A8%B3%E6%80%81
- ↑ Eagleman, David (2001). "Visual Illusions and Neurobiology" (PDF). Nature Reviews Neuroscience. 2 (12): 920–926. doi:10.1038/35104092. Archived from the original (PDF) on 2007-09-27.
{{cite journal}}: Unknown parameter|deadurl=ignored (help)
本中文词条由舒寒参与编译,思无涯咿呀咿呀编辑,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。