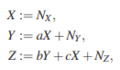“忠实性假设”的版本间的差异
Dario Zhang(讨论 | 贡献) |
(→定义) |
||
| 第6行: | 第6行: | ||
(总体:统计学概念,指包含所研究的全部个体(数据)的集合) | (总体:统计学概念,指包含所研究的全部个体(数据)的集合) | ||
| − | + | 考虑一个多变量联合概率分布<math>P_{X}</math>和一个有向无环图DAG <math>\mathcal{G}</math>. | |
| − | + | 定义:联合概率分布<math>P_{X}</math>对于DAG <math>\mathcal{G}</math>满足因果忠实性,如果<ref name="Elements">Peters Jonas,Janzing Dominik,Schlkopf Bernhard (2017) [https://pattern.swarma.org/paper?id=5c93b918-c3ba-11eb-8fd5-0242ac170007 Elements of Causal Inference: Foundations and Learning Algorithms].</ref>: | |
<math>A \perp\!\!\!\perp B \mid C \Rightarrow A \perp\!\!\!\perp_{\mathcal{G}} B \mid C</math> | <math>A \perp\!\!\!\perp B \mid C \Rightarrow A \perp\!\!\!\perp_{\mathcal{G}} B \mid C</math> | ||
| − | + | 对于所有不相交的顶点(变量)集 A,B,C 均成立。 | |
这个定义暗示了一个与全局马尔可夫条件相反的结论: | 这个定义暗示了一个与全局马尔可夫条件相反的结论: | ||
2021年6月3日 (四) 21:08的版本
因果忠实性
定义
假设某个总体是忠实的,那就是假设其中发生的任何独立性都不是来自不可思议的巧合,而是来自结构。[1] (总体:统计学概念,指包含所研究的全部个体(数据)的集合)
考虑一个多变量联合概率分布[math]\displaystyle{ P_{X} }[/math]和一个有向无环图DAG [math]\displaystyle{ \mathcal{G} }[/math].
定义:联合概率分布[math]\displaystyle{ P_{X} }[/math]对于DAG [math]\displaystyle{ \mathcal{G} }[/math]满足因果忠实性,如果[2]:
[math]\displaystyle{ A \perp\!\!\!\perp B \mid C \Rightarrow A \perp\!\!\!\perp_{\mathcal{G}} B \mid C }[/math]
对于所有不相交的顶点(变量)集 A,B,C 均成立。
这个定义暗示了一个与全局马尔可夫条件相反的结论:
[math]\displaystyle{ A \perp\!\!\!\perp_{\mathcal{G}} B \mid C \Rightarrow A \perp\!\!\!\perp B \mid C }[/math]
乍一看,忠实性并不是很直观。 我们现在给出一个马尔可夫分布的例子,但对于给定的 DAG [math]\displaystyle{ \mathcal{G_{1}} }[/math] 不忠实。 这是通过使两条路径相互抵消并创建图结构未暗示的独立性来实现的。
违反忠实性[2]
考虑下图:
我们首先看一个线性高斯 [math]\displaystyle{ SCM }[/math] 对应于左图[math]\displaystyle{ \mathcal{G_{1}} }[/math]。
正态分布的噪声变量[math]\displaystyle{ N_{X} ∼ \mathcal{N} (0,\sigma^2_X ) }[/math]、[math]\displaystyle{ N_{Y} ∼ \mathcal{N} (0,\sigma^2_Y ) }[/math] 和 [math]\displaystyle{ N_{Z} ∼ \mathcal{N} (0,\sigma^2_Z ) }[/math] 共同独立。 这是带有图[math]\displaystyle{ \mathcal{G_{1}} }[/math] 的线性高斯 [math]\displaystyle{ SCM }[/math] 的示例。 现在,如果
[math]\displaystyle{ a \cdot b + c = 0 }[/math] (1)
由于我们获得 [math]\displaystyle{ X \perp\!\!\!\perp Z }[/math],因此分布不忠实于[math]\displaystyle{ \mathcal{G_{1}} }[/math],这不是图结构所暗示的。读者可以轻松验证存在带有DAG [math]\displaystyle{ \mathcal{G_{2}} }[/math]的SCM引出相同分布。
为了在前面的例子中获得额外的独立性,我们必须“调整”系数,使得两条路径在(1)中相互抵消。 Spirtes等人[2000, Theorem 3.2]对于线性模型表明,如果我们假设系数是从正密度中随机抽取的,那么这种情况发生的概率为零。
上例中的分布对于[math]\displaystyle{ \mathcal{G_{2}} }[/math]是忠实的,但对于[math]\displaystyle{ \mathcal{G_{1}} }[/math]则不是。尽管如此,对于这两个模型,如果没有任何参数归零,则满足因果最小性。换句话说,该分布对于[math]\displaystyle{ \mathcal{G_{1}} }[/math] 或[math]\displaystyle{ \mathcal{G_{2}} }[/math]的任何真子图都不是马尔可夫的,因为删除任何边将对应于在分布中不成立的新(条件)独立性; 注意[math]\displaystyle{ \mathcal{G_{2}} }[/math]不是[math]\displaystyle{ \mathcal{G_{1}} }[/math]的真子图。 然而,它是[math]\displaystyle{ \mathcal{H} }[/math]的真子图,因此,该分布不满足关于[math]\displaystyle{ \mathcal{H} }[/math]的因果最小性。通常,因果最小性弱于忠实性。
通过假定因果图满足因果马尔可夫性,我们假设此因果图产生的所有总体都具有通过对其应用d分离而获得的独立性关系。 但是,并不能因此而得出结论,这些总体恰好具有这些独立性关系并且没有其他独立性关系。[1]
示例[1]
图1中描述了运动,吸烟和健康之间的关系,其中+和-分别表示正向和抑制性关系。
在这种结构可能产生的某些分布中,可能存在巧合,如果吸烟对健康有直接的负面影响,但是吸烟对运动有积极的影响(可能看起来很奇怪),而锻炼对健康有积极的影响,那么吸烟可以直接抑制健康并间接改善健康。
如果这两种效应恰好完全平衡并因此抵消,那么吸烟与健康之间可能根本就没有关联。
在这种情况下,我们说总体分布不忠实于产生它的因果图。
参考文献
- ↑ 1.0 1.1 1.2 Scheines R. (1997) An introduction to causal inference.
- ↑ 2.0 2.1 Peters Jonas,Janzing Dominik,Schlkopf Bernhard (2017) Elements of Causal Inference: Foundations and Learning Algorithms.