“结构因果模型”的版本间的差异
| 第202行: | 第202行: | ||
当因果模型是现实的合理表示并且满足后门准则时,则对于线性关系可以将'''<font color="#ff8000"> 偏回归系数 Partial Regression Coefficients </font>'''作为'''<font color="#ff8000"> (因果)路径系数 (Causal) Path Coefficients </font>'''。 | 当因果模型是现实的合理表示并且满足后门准则时,则对于线性关系可以将'''<font color="#ff8000"> 偏回归系数 Partial Regression Coefficients </font>'''作为'''<font color="#ff8000"> (因果)路径系数 (Causal) Path Coefficients </font>'''。 | ||
| − | :<math> P(Y|do(X))=\sum_z{P(Y|X,Z)P(Z)}</math> | + | :<math> P(Y|do(X))=\sum_z{P(Y|X,Z=z)P(Z=z)}</math> |
=== 前门调整 Frontdoor Adjustment === | === 前门调整 Frontdoor Adjustment === | ||
2021年6月5日 (六) 14:42的版本
在科学哲学中, 因果模型 Causal Model(或 结构因果模型 Structural Causal Model)是描述系统因果机制的概念模型。因果模型可以通过提供清晰的规则来决定需要考虑/控制哪些自变量,从而改进研究设计。
因果模型可以从现有的观察数据中回答一些问题,而无需进行随机对照实验等干预性研究。一些干预性研究由于伦理或实践的原因是不合适的,这意味着如果没有一个因果模型,一些假设就无法被检验。
因果模型可以帮助解决 外部有效性 External Validity问题(一项研究的结果是否适用于未研究的总体)。在某些情况下,因果模型可以允许多项研究的数据合并起来回答任何单个数据集都无法回答的问题。
因果模型是可证伪的,因为如果一些因果模型与数据不匹配,这些因果模型就必须作为无效模型而被拒绝接受。因果模型还必须使得研究相关现象的科学家们信服。
因果模型在信号处理、流行病学和机器学习中都有应用。
定义 Definition
因果模型是表示单个系统或群体内因果关系的数学模型。它有助于从统计数据中推断因果关系,可以教会我们关于因果关系的认识论,并展现因果关系和概率之间的关系。它还被应用于哲学家感兴趣的主题,例如反事实逻辑、决策理论和实际因果关系分析。[2]
Judea Pearl将因果模型定义为一个有序的三元组[math]\displaystyle{ \langle U, V, E\rangle }[/math],其中 U 是一组外生变量,其值由模型外部的因素决定;V 是一组内生变量,其值由模型内部的因素决定;E 是一组结构方程,把每个内生变量的值表示为 U 和 V 中其他变量值的函数。
历史 History
亚里士多德定义了因果关系的分类法,包括质料因、形式因、动力因、目的因。休谟更偏爱反事实,他拒绝了亚里士多德的分类法。有段时间,他否认物体本身具有使得一个物体成为原因而另一个物体成为结果的“力量”。后来,他接受了“如果第一物体还没存在,第二个根本不存在”的观点(“but-for”因果关系)。
19世纪末,统计学学科开始形成。经过多年努力确定诸如生物遗传等领域的因果规则后,高尔顿引入了 均值回归 Mean Regression 的概念(以二年生症候群为缩影),后来这将他引向了非因果的相关性概念。
作为一个实证主义者,皮尔逊将因果的概念从许多科学中去除,他认为因果关系是一种无法证明的特殊的关联,并引入相关系数作为关联强度的度量方法。他写道: “作为运动原因的力,与作为成长原因的树神完全一样”,而因果关系只是“现代科学高深奥秘中的迷信”。皮尔逊在伦敦大学学院创立了期刊“Biometrika”和生物识别实验室,该实验室成为了统计领域的全球领导者。
1908年,Hardy和Weinberg通过重拾孟德尔遗传律,解决了导致高尔顿放弃因果关系的性状稳定问题。
1921年,Wright的路径分析成为因果模型和因果图的理论雏形。他开发了这种路径分析方法,试图同时阐明遗传、发育和环境对豚鼠皮毛模式的相对影响。他通过一个分析过程如何解释豚鼠出生体重、子宫内时间和产仔数之间的关系来支持他旁门左道的观点。杰出的统计学家对这些想法的反对使因果关系在接下来的40年中被家畜育种学家之外的科学家所忽略。取而代之的是,科学家们依赖于相关性, partly at the behest of Wright's critic (and leading statistician), Fisher。唯一的例外是一名叫Burks的学生,在1926年首先应用路径图来表示中介影响,并断言保持中介变量恒定会引起误差。她可能独立地发明了路径图。
1923年,Neyman提出了潜在结果(potential outcome)的概念,但是直到1990年他的论文才被从波兰语翻译成英语。
1958年,Cox警告说,仅当Z高概率不被自变量影响的时,控制变量Z才有效。
20世纪60年代,Duncan、Blalock、Goldberger等人重新发现了路径分析。Duncan在阅读Blalock关于路径图的著作时,想起了二十年前Ogburn的一次演讲,其中提到了Wright的论文,而后又提到了Burks。
社会学家最初将因果模型称为 结构方程模型 Structural Equation Modeling ,但一旦它成为教条式方法就失去了效用,导致一些从业者拒绝与因果关系的任何联系。经济学家采用了路径分析的代数部分,称其为 联立方程建模 Simultaneous Equation Modeling 。但是,经济学家仍然避免将因果含义赋予他们的方程式。
Wright在发表第一篇论文60年后,根据Karlin等人的批评,发表了一篇概述该论文的文章,该论文反对仅处理线性关系,而鲁棒的、非模型的数据表示方式则更具揭示性。
1973年,Lewis提倡用but-for因果关系(反事实)代替相关性。他提到了人类具有想象某个原因是否发生和结果仅在原因后发生的不同可选世界的能力。1974年Rubin引入了“潜在结果”(potential outcome)的概念,作为询问因果问题的语言。
1983年,Cartwright提出与一个结果因果相关的任何因子都是有条件的,不再以简单的概率作为唯一指导。
1986年,Baron和Kenny引入了检测和评估线性方程系统中的中介的原理。截至2014年,他们的论文是有史以来被引用最多的第33篇。那年,Greenland和Robins通过考虑反事实,引入了“可交换性”方法,来处理混杂问题。他们提出评估如果治疗组没有接受治疗会给治疗组带来什么后果,并将其结果与对照组进行比较。如果结果一致,说明没有混杂因子。
哥伦比亚大学设有因果人工智能实验室,该实验室正试图将因果建模理论与人工神经网络联系起来。
因果关系之梯 Ladder of Causation
Judea Pearl的因果元模型涉及三个层次的抽象,他称之为因果之梯。最低层的“关联”(看到/观察)需要感知输入数据中的规律性或模式,用相关性表示。中间层的“干预”(做)可以预测有意识行动的后果,用因果关系表示。最高层的“反事实”(想象)涉及构建部分世界的理论,该理论解释为什么特定行为会产生特定后果,以及在没有此行为的情况下会发生什么。
关联 Association
如果观察一个对象改变了观察另一个对象的可能性,则这个对象与另一个对象相关联。例子:购买牙膏的购物者也更有可能购买牙线。数学上用
- [math]\displaystyle{ P (买牙线 | 买牙膏) }[/math]
表示已知一个人购买牙膏时的其购买牙线的可能性。关联也可以通过计算两个事件的相关性来衡量。关联并不意味着因果。一个事件可能导致另一个事件,反过来也可能,或者两个事件都可能由某个第三事件引起(牙医对口腔健康的宣传使得购物者同时购买牙线和牙膏)。
干预 Intervention
该层涉及事件之间的特定因果关系。因果是通过实验性地执行影响事件的一些动作来评估。例如:如果我们将牙膏的价格提高一倍,那么人们购买牙线的概率将是多少?因果无法通过检验历史信息来确定,因为可能存在其他因素同时影响这两个变量,比如存在牙膏价格变化的其他原因,而且这种原因会影响牙线的价格(例如两种商品的关税增加)。数学上用
- [math]\displaystyle{ P (牙线价格 | do(牙膏价格)) }[/math]
表示这种概率。其中do是一个算子,表示对谁做实验性干预(如价格翻倍)。这个算子指示了要在创造所需效果的世界中进行最小的变化,即在现实模型上进行尽可能小的改变的“小手术”。
反事实 Counterfactuals
最高层的反事实涉及对过去事件的其他可能版本的考虑,或者考虑同一实验个体中在不同情况下会发生的情况。例如,如果当初那家商店的牙线价格翻了一番,那么当时那些购买牙膏的购物者仍然会购买牙线的可能性是多少?
- [math]\displaystyle{ P (买牙线 | 买牙膏, 当初牙线价格翻倍) }[/math]
反事实可以表明存在因果关系。回答反事实的模型允许进行精确的干预,这些干预的后果可被预测。在极端情况下,这样的模型被人们认为是物理定律(如惯性:若不将力施加到静止物体上物体将不会移动)。
因果 Causality
因果和关联 Causality vs Correlation
统计学涉及分析多个变量之间的关系。传统上,这些关系被描述为相关性,即没有任何隐含因果关系的关联。因果模型试图通过添加因果关系的概念来扩展此框架,在因果关系中,一个变量的变化导致其他变量的变化。
20世纪因果的定义完全依赖于概率或关联。如果一个事件 X 增加了另一个事件 Y 的可能性,则认为它会导致另一个事件。在数学上,这表示为:
- [math]\displaystyle{ P (Y | X) \gt P(Y) }[/math]
这样的定义是不充分的,因为可能有其他关系(例如, X 和 Y 的共同原因)可以满足该条件。因果与因果之梯的第二层有关。关联处于第一层,仅向第二层提供证据。
之后的定义试图通过以背景因素为条件来解决这种歧义。数学上表示为:
- [math]\displaystyle{ P (Y | X, K = k) \gt P(Y| K = k) }[/math]
其中 K 是背景变量的集合, k 表示特定语境中背景变量的值。但是,只要概率是唯一准则,那么所需的背景变量集是难以确定的。
定义因果的其他尝试包括 格兰杰因果 Granger Causality ,这是一种统计假设检验,在经济学中,可以通过衡量用一个时间序列的过去值预测另一个时间序列的未来值的能力,来评估序列间的因果。
类型 Types
原因可以是必要的、充分的、部分的以及它们的组合。
必要因 Necessary Causes
对于 y 的必要因 x ,y 的存在意味着 x 在此前发生了。但是 x 的存在不意味着y会发生。必要因也被称为“若非(but-for)”因,即y不会发生若非 x 发生。
充分因 Sufficient Causes
对于y的充分因x,x的存在意味着y接下来会发生。然而另一个原因z也可能独立地造成y的发生。即y的发生不要求x的发生。
部分因 Contributory Causes
对于y的部分因x,x的存在会增加y的似然。如果似然是100%,那么x就是充分的。部分因也是必要的。
模型 Model
因果图 Causal Diagram
因果图是一个有向图,它显示了因果模型中变量间的因果关系。因果图包括一组变量(或节点),每个节点通过箭头连接到一个或多个对其具有因果效应的其他节点。箭头描绘了因果的方向,例如,将变量 A 和 变量B 以指向 B 的箭头相连表示A的变化以某种概率导致B的变化。一条路径是两个节点间沿着因果箭头的图的遍历。
因果图包括 因果环图 Causal Loop Diagrams , 有向无环图 Directed Acyclic Graphs 和 鱼骨图 Ishikawa diagrams。
因果图和它们的定量概率无关,对这些概率的更改不需要修改因果图。
模型元素 Model elements
因果模型具有形式结构,其元素具有特定的属性。
接合方式 Junction Patterns
三个节点的连接类型有三种,分别是线型的链,分支型的叉和合并型的对撞。
链接合 Chain
链接合是直线连接,箭头从原因指向结果。在这个模型中,B是中介变量,因为它调节了 A 对 C 的影响。
- [math]\displaystyle{ A \rightarrow B \rightarrow C }[/math]
叉接合 Fork
在叉接合中,一个原因有多种结果,这两种结果有一个共同的原因。 A 和 C 之间存在非因果的虚假相关性,可以通过把 B 作为条件(选取B的特定值)来消除虚假相关性。
- [math]\displaystyle{ A \leftarrow B \rightarrow C }[/math]
“把B作为条件”是指“给定B”(即B取某个值)。 某些情况下叉接合是混杂因子:
- [math]\displaystyle{ A \leftarrow B \rightarrow C \rightarrow A }[/math]
在这样的模型中, B 是 A 和 C 的共同原因( C 也是 A 的原因),这使B成为 混杂因子 Confounder 。
对撞 Collider
在对撞接合中,多种原因会影响一种结果。以 B 为条件( B 取特定值)通常会揭示 A 与 C 之间的非因果的负相关。这种负相关被称为对撞偏差和“辩解”效应,即 B 解释了 A 与 C 之间的相关性。 A 和 C 两者都是影响 B 的必要因时,该相关性是正的。
- [math]\displaystyle{ A \rightarrow B \leftarrow C }[/math]
节点类型 Node Types
中介变量 Mediator
中介变量节点修改了其他原因对结果的影响(这与原因简单地影响结果不同)。例如,在上面的链结构中,B是中介变量,因为它修改了 C 的间接原因 A 对结果变量 C 的影响。
混杂因子 Confounder
混杂因子节点影响多个结果,从而在它们之间产生正相关。
工具变量 Instrumental Variable
满足如下条件的是工具变量:(1)有通往结果变量的路径(2)没有通往其他原因变量(解释变量)的路径(3)对结果没有直接影响。 回归系数可以用作工具变量对结果的因果影响的估计,只要该影响不被混杂即可。通过这种方式,工具变量允许对因果因子进行量化,而无需有关混杂因子的数据。 例如,给定模型:
- [math]\displaystyle{ Z \rightarrow X \rightarrow Y \leftarrow U \rightarrow X }[/math]
Z是一种工具变量,因为它有一条通往结果Y的路径,并且不受U的混杂。
孟德尔随机化 Mendelian randomization
定义:孟德尔随机化使用已知功能的基因,来观察研究中可改变的部分对疾病的因果关系。
由于基因在人群中随机变化,基因的存在通常可以视为工具变量。这意味着在许多情况下,可以使用观察性研究中的回归来量化因果关系。
关联 Associations
独立性条件 Independence Conditions
独立性条件是用于确定两个变量是否彼此独立的规则。如果一个变量的值不直接影响另一个变量的值,则两个变量是独立的。多个因果模型可以共享独立条件。例如,模型
- [math]\displaystyle{ A \rightarrow B \rightarrow C }[/math]
和
- [math]\displaystyle{ A \leftarrow B \rightarrow C }[/math]
具有相同的独立条件,因为 B 作为条件时 A 和 C 独立。但是,这两个模型的含义不同,还可能与数据不符(也就是说,如果观测数据显示在 B 作为条件后显示了 A 和 C 之间的关联,那么这两个模型都是不正确的)。相反,数据无法显示这两个模型中的哪个是正确的,因为它们具有相同的独立性条件。
将变量作为条件是进行假设实验的一种机制。将变量作为条件即在条件变量的给定值下分析其他变量的值。在第一个示例中, B 作为条件意味着给定 B 的取值的观察,此时不应显示出 A 和 C 之间的依赖关系。如果存在这种依赖关系,则该模型是不正确的。非因果模型无法进行这种区分的,因为它们不会做出因果断言。
混杂/去混杂 Confounder/Deconfounder
设计相关性研究的基本要素是确定对所研究变量的潜在混杂影响。控制这些变量是为了消除这些影响。但是,这些混杂变量无法被先验地正确确定。因此,一项研究可能会控制不相关的变量,甚至(间接地)控制了所研究的变量。 因果模型为识别恰当的混杂变量提供了一种鲁棒的技术。形式上,如果“ Y 通过不经过 X 的路径与 Z 关联”,则 Z 是混杂因素。这些混杂变量通常可以使用其他研究所收集的数据来确定。数学上,如果
- [math]\displaystyle{ P(Y|X) \neq P(Y|do(X)) }[/math]
那么X是Y的混杂因子。
在此之前,混杂因子的不正确的定义包括:
(1)“与X和Y都相关的任何变量。”
(2)Y和未观测变量Z有关联
(3)不相容性:“原始相对风险和潜在混杂因素调整后产生的相对风险”之间的差异
(4)流行病学:在大范围总体中与 X 相关的变量,而在未接触 X 的人群中与 Y 相关的变量。
在如下模型中,上述定义是有缺陷的:
- [math]\displaystyle{ X \rightarrow Z \rightarrow Y }[/math]
Z 符合定义,但 Z 是中介变量,而不是混杂因子,并且是控制结果的一个例子。
在模型中
- [math]\displaystyle{ X \leftarrow A \rightarrow B \leftarrow C \rightarrow Y }[/math]
传统上, B 被认为是混杂因子,因为它与 X 和 Y 关联,但 B 既不在因果路径上,也不是因果路径上任何节点的后代。控制 B 将使 B 成为混杂因子。这被称为M偏差。
后门调整 Backdoor Adjustment
为了分析因果模型中X对Y的因果效应,我们需要针对所有混杂变量进行调整(去混杂)。为了确定混杂变量的集合,我们需要(1)通过该集合阻塞X和Y之间的每个非因果路径(2)不破坏任何原有的因果路径(3)不创建任何虚假路径。
定义:从X到Y的后门路径是指,从从 X 到 Y 的任何以指向 X 的箭头为开始的路径。
定义:给定模型中的一对有序变量(X,Y),如果(1)混杂变量集Z中没有X的后代,(2)X和Y之间的所有后门路径都被Z中的混杂变量阻断,则称混杂变量集Z满足后门准则。
如果( X , Y )满足后门准则,则在控制混杂变量集 Z 时 X 和 Y 是无混杂的。除了混杂变量外,没有必要控制其他任何变量。后门准则是找到混杂变量 Z 的集合的充分条件,但不是分析 X 对 Y 的因果效应必要条件。
当因果模型是现实的合理表示并且满足后门准则时,则对于线性关系可以将 偏回归系数 Partial Regression Coefficients 作为 (因果)路径系数 (Causal) Path Coefficients 。
- [math]\displaystyle{ P(Y|do(X))=\sum_z{P(Y|X,Z=z)P(Z=z)} }[/math]
前门调整 Frontdoor Adjustment
如果阻塞路径的所有元素都不可观测,则后门路径不可计算,但是如果所有从 X 到 Y 的路径都有元素 z ,并且 z 到 Y 没有开放的路径,那么我们可以使用 z 的集合 Z 来测量[math]\displaystyle{ P(Y|do(X)) }[/math]。实际上 Z 作为 X 的代理时有一些条件。
定义:前门路径是这样的直接因果路径,(1)Z阻断了所有X到Y的有向路径(2)X到Y没有后门路径(3)所有Z到Y的后门路径都被X阻断。
以下式子通过将前门路径上的变量集Z作条件,将含有do的表达式转化成不含do的表达式:
- [math]\displaystyle{ P(Y|do(X))=\sum_z{[P(Z=z|X)\sum_x{P(Y|X=x,Z=z)P(X=x)}]} }[/math]
假定上述概率涉及到的观察数据可用,则无需进行实验即可计算出最终概率,而不管是否存在其他混杂路径且无需进行后门调整。
干预 Interventions
查询 Queries
查询是根据特定模型提出的问题。通常通过进行干预实验来回答这些问题。“干预”会设定模型中一个变量的值并观察结果。从数学上讲,此类查询采用以下形式(例子):
- [math]\displaystyle{ P(牙线价格|do(牙膏价格)) }[/math]
其中do算子表示该实验明确修改牙膏的价格。图模型上看,这可以阻止任何可能影响该变量的因果变量。这消除了所有指向实验变量(牙膏价格)的因果箭头。
do算子也可以应用于多个变量(使它们取值固定)进行更复杂的查询。
Do演算 Do-calculus
Do演算是一组可用于将一个表达式转换为另一个表达式的一系列操作,其总体目标是将包含do算子的表达式转换为不包含do算子的表达式。不含do算子的表达式可以仅从观察数据中估计出来,而无需进行实验干预;而实验干预可能是代价大,耗时长甚至是不道德的(例如,要求受试者吸烟)。Do演算的规则集是完备的,可用于推导出该系统中的每个真命题。有一种算法可以确定对于给定模型,是否可以在多项式时间内求解。
do演算规则集 Do-Calculus Rules
该运算包括了三条涉及do算子的条件概率变换规则。其中规则1和3都是显然的,但规则2有些微妙。下面给出表达do演算规则集的三种版本。
版本1
该版本是维基百科上do演算的表达方式。
规则1用来增删观测:
- [math]\displaystyle{ P(Y|do(X),Z,W)=P(Y|do(X),Z) }[/math]
在删除所有指向X的箭头的图中,Z阻塞了所有从W到Y的路径。
规则2用来互换干预和观测:
- [math]\displaystyle{ P(Y|do(X),Z)=P(Y|X,Z) }[/math]
在原图中Z满足后门准则。
规则3用来增删干预:
- [math]\displaystyle{ P(Y|do(X))=P(Y) }[/math]
在原图中X和Y间没有因果路径。
版本2
该版本是Judea Pearl的《Causality: Models, Reasoning and Inference (2nd Edition)》中的表达方式。
规则1用于增删观测:在 [math]\displaystyle{ G_{\overline{X}} }[/math] 中,当给定[math]\displaystyle{ X }[/math]和[math]\displaystyle{ W }[/math],有[math]\displaystyle{ Y }[/math]和[math]\displaystyle{ Z }[/math]条件独立时,则
- [math]\displaystyle{ P(Y|do(X),Z,W)=P(Y|do(X),Z) }[/math]
规则2用于互换干预和观察:在 [math]\displaystyle{ G_{\overline{X}\underline{Z}} }[/math] 中,当给定[math]\displaystyle{ X }[/math]和[math]\displaystyle{ W }[/math],有[math]\displaystyle{ Y }[/math]和[math]\displaystyle{ Z }[/math]条件独立时,则
- [math]\displaystyle{ P(Y|do(X),do(Z),W)=P(Y|do(X),Z,W) }[/math]
规则3用于增删干预:在 [math]\displaystyle{ G_{\overline{X}\underline{Z(W)}} }[/math] 中,当给定[math]\displaystyle{ X }[/math]和[math]\displaystyle{ W }[/math],有[math]\displaystyle{ Y }[/math]和[math]\displaystyle{ Z }[/math]条件独立时,则
- [math]\displaystyle{ P(Y|do(X),do(Z),W)=P(Y|do(X),W) }[/math]
其中 [math]\displaystyle{ Z(W) }[/math] 表示 [math]\displaystyle{ Z - An(W)_{ G_{ \overline{X} } } }[/math] , [math]\displaystyle{ An(W)_{G} }[/math] 表示[math]\displaystyle{ W }[/math]在图[math]\displaystyle{ G }[/math]中的祖先集([math]\displaystyle{ W }[/math]及其祖先节点构成的点集), [math]\displaystyle{ G_{\overline{X}} }[/math] 表示删除[math]\displaystyle{ G }[/math]中所有指向[math]\displaystyle{ X }[/math]节点的边后得到的子图, [math]\displaystyle{ G_{\overline{X}\underline{Z}} }[/math] 表示删除[math]\displaystyle{ G }[/math]中所有指向[math]\displaystyle{ X }[/math]节点的边和从[math]\displaystyle{ Z }[/math]指向其他节点的边后得到的子图。
版本3
该版本是Daphne Koller和Nir Friedman的《概率图模型:原理与技术》一书中的表达方式。
规则1用于增删观测:在 [math]\displaystyle{ G_{\overline{Z}}^{+} }[/math] 中,当给定[math]\displaystyle{ Z }[/math]和[math]\displaystyle{ X }[/math],有[math]\displaystyle{ W }[/math]和[math]\displaystyle{ Y }[/math] 有向分离 d-seperated 时,则
- [math]\displaystyle{ P(Y|do(Z),X,W)=P(Y|do(Z),X) }[/math]
规则2用于互换干预和观察:在 [math]\displaystyle{ G_{\overline{Z}}^{+} }[/math] 中,当给定[math]\displaystyle{ X }[/math]、[math]\displaystyle{ Z }[/math]、[math]\displaystyle{ W }[/math],有[math]\displaystyle{ Y }[/math]和 [math]\displaystyle{ \hat{X} }[/math] 有向分离时,则
- [math]\displaystyle{ P(Y|do(Z),do(X),W)=P(Y|do(Z),X,W) }[/math]
规则3用于增删干预:在 [math]\displaystyle{ G_{\overline{Z}}^{+} }[/math] 中,当给定[math]\displaystyle{ Z }[/math]和[math]\displaystyle{ W }[/math],有[math]\displaystyle{ Y }[/math]和 [math]\displaystyle{ \hat{X} }[/math] 有向分离时,则
- [math]\displaystyle{ P(Y|do(Z),do(X),W)=P(Y|do(Z),W) }[/math]
其中 [math]\displaystyle{ G_{\overline{Z}}^{+} }[/math] 表示删除[math]\displaystyle{ G }[/math]中所有指向[math]\displaystyle{ Z }[/math]节点的边,添加独立决策变量[math]\displaystyle{ \hat{Z} }[/math]唯一指向[math]\displaystyle{ Z }[/math],从而得到的拓展图。
扩展 Entensions
这些规则并不意味着任何查询都能移除do算子。有些情况下,将一个不能进行的操作换成另一个可以进行的操作也是有意义的。例如:
- [math]\displaystyle{ P(心脏病|do(血胆固醇))=P(心脏病|do(饮食)) }[/math]
反事实 Counterfactuals
反事实考虑那些无法从数据中得到的概率,如一个不吸烟的人在过去重度吸烟的话,他现在会不会得癌症。
潜在结果 Potential Outcome
定义:Y的潜在结果是“如果X被赋值为x,对于个体u来说Y会怎么样”。数学上可以表达为
- [math]\displaystyle{ Y_X=Y_x(u) }[/math]
潜在结果是在个体u的层次定义的。
传统的潜在结果是数据驱动的,而非模型驱动的,这限制了它辨析因果关系的能力。它将因果问题当作数据缺失问题,甚至在标准场景下都会给出错误的回答。
因果推断 Causal inference
在因果模型的语境中,潜在结果是被从因果角度解释的,而非从统计角度解释。
因果推断的第一定律意味着潜在结果
- [math]\displaystyle{ Y_x(u) }[/math]
可以被这样计算:将因果模型M中指向X的箭头删除,计算特定的x的结果。形式上,
- [math]\displaystyle{ Y_x(u)=Y_{M_x}(u) }[/math]
可移植性 Transportability
即使因果模型及对应的相关数据不同,因果模型也提供了一种工具来集成跨数据集的数据,称为移植。例如,调查数据可以与随机对照实验数据合并。移植提供了一个外部有效性问题的解决方案,即一项研究是否可以在不同的背景下应用。
一,如果两个模型在所有相关变量上都匹配,并且已知来自其中一个模型的数据是无偏的,则可以使用一个总体的数据得出关于另一个总体的结论。
二,已知数据存在偏差,则重加权可以允许模型在数据集间移植。
三,可以从不完整的数据集中得出结论。
四,可以组合(移植)来自多个总体的研究数据,以得出有关未观测总体的结论。
五,结合多个研究的估计值(例如P(W|X))可以提高结论的准确性。
do演算为移植提供了一个一般性准则:目标变量可以通过一系列不涉及任何“差异”变量(能够区分两个总体的变量)的do运算转换为另一个表达式。有一个类似的规则适用于参与者相对不同的研究。
贝叶斯网络 Bayesian network
因果模型可以用贝叶斯网实现。贝叶斯网络可用于提供事件的逆概率(给定结果,反推具体原因的概率是多少)。这就需要准备一个条件概率表,显示所有可能的输入和结果以及相关的概率。 例如,给定疾病和针对疾病的检验的两变量模型,条件概率表的形式为:
| Test | ||
|---|---|---|
| 疾病 | 阳性 | 阴性 |
| 阴性 | 12 | 88 |
| 阳性 | 73 | 27 |
根据该表,当患者没有疾病时,测试为阳性的可能性为12%。 尽管这对于小问题很容易解决,但是随着变量数量及其相关状态的增加,概率表(以及相关的计算时间)呈指数增长。 贝叶斯网络在商业上可用于如无线数据纠错和DNA分析之类的应用中。
不变量/语境Invariants/Context
因果的不同概念涉及不变关系的概念。在识别手写数字的情况下,数字形状决定含义,因此形状和含义是不变量,改变形状会改变含义。其他属性则没有此性质(如颜色)。此不变性对于在各种非不变量所构成语境中生成的数据集都应满足。与其使用汇总的数据集进行学习评估因果关系,不如对一个数据集进行学习并对另一数据集进行测试,这可以帮助将变化属性与不变量区分开。
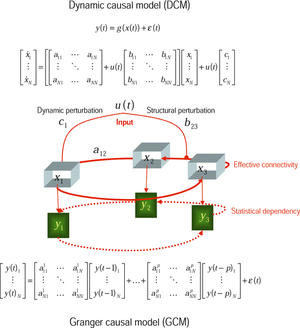
- ↑ Karl Friston (Feb 2009). "Causal Modelling and Brain Connectivity in Functional Magnetic Resonance Imaging". PLOS Biology. 7 (2): e1000033. doi:10.1371/journal.pbio.1000033. PMC 2642881. PMID 19226186.
- ↑ Hitchcock, Christopher (2018), "Causal Models", in Zalta, Edward N. (ed.), The Stanford Encyclopedia of Philosophy (Fall 2018 ed.), Metaphysics Research Lab, Stanford University, retrieved 2018-09-08