“分层随机试验”的版本间的差异
| 第8行: | 第8行: | ||
== 分层随机试验步骤 == | == 分层随机试验步骤 == | ||
| − | + | 分层随机试验在目标总体异<font color="#ff8000"> '''质性 | |
| − | Heterogeneous'''</font>的情况下非常有用, <font color="#32cd32"> 它能有效地显示研究中的趋势或特征在不同阶层(或 地层)effectively displays how the trends or characteristics under study differ between strata.</font>之间的差异。<ref name=":3" />当进行分层随机试验时,应采取以下8个步骤:<ref name=":4">{{Cite web|url=https://www.statisticshowto.com/stratified-random-sample/|title=Stratified Random Sample: Definition, Examples|last=Stephanie|date=Dec 11, 2013|website=Statistics How To|language=en-US|access-date=2020-04-07}}</ref><ref name=":5">{{Cite web|url=https://www.questionpro.com/blog/stratified-random-sampling/|title=Stratified Random Sampling: Definition, Method and Examples|date=2018-03-13|website=QuestionPro|language=en|access-date=2020-04-07}}</ref> | + | Heterogeneous''' </font>的情况下非常有用, <font color="#32cd32"> 它能有效地显示研究中的趋势或特征在不同阶层(或 地层)effectively displays how the trends or characteristics under study differ between strata.</font>之间的差异。<ref name=":3" />当进行分层随机试验时,应采取以下8个步骤:<ref name=":4">{{Cite web|url=https://www.statisticshowto.com/stratified-random-sample/|title=Stratified Random Sample: Definition, Examples|last=Stephanie|date=Dec 11, 2013|website=Statistics How To|language=en-US|access-date=2020-04-07}}</ref><ref name=":5">{{Cite web|url=https://www.questionpro.com/blog/stratified-random-sampling/|title=Stratified Random Sampling: Definition, Method and Examples|date=2018-03-13|website=QuestionPro|language=en|access-date=2020-04-07}}</ref> |
2021年6月8日 (二) 22:19的版本
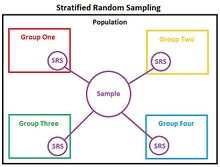
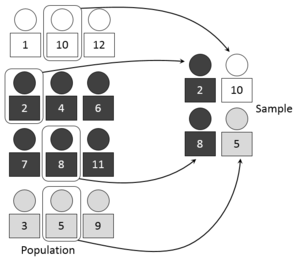
在统计学中, 分层随机试验 Stratified randomization 是一种抽样方法,首先将整个研究 总体 Population 层为具有相同属性或特征的子群,称为 分层 Attributes ,然后从分层组中进行简单随机抽样,在抽样过程的任何阶段,随机、完全偶然地无偏抽取同一子群中的元素。[1][2]分层随机试验被认为是 分层抽样 Stratified sampling 的一个细分。当共享属性部分存在,并且在被调查总体的不同亚群之间有很大差异时,应该采用分层随机试验。因此,在取样过程中需要特别考虑或明确区分。[3]这种抽样方法应区别于 整群抽样方法 Cluster sampling ,整群抽样方法是在整个群体中选择一个简单的随机抽样来代表整个总体,或分层系统抽样方法,在分层过程之后进行 系统抽样 Systematic sampling 。分层随机抽样有时也称为 定额随机抽样 Quota random sampling 。[1]
分层随机试验步骤
分层随机试验在目标总体异 质性
Heterogeneous 的情况下非常有用, 它能有效地显示研究中的趋势或特征在不同阶层(或 地层)effectively displays how the trends or characteristics under study differ between strata.之间的差异。[1]当进行分层随机试验时,应采取以下8个步骤:[4][5]
- Define a target population.
Define a target population.
Define a target population.
- Define stratification variables and decide the number of strata to be created. The criteria for defining variables for stratification include age, socioeconomic status, nationality, race, education level and others and should be in line with the research objective. Ideally, the number of 4-6strata should be employed, as any increase in stratification variables will raise the probability for some of them to cancel out the impact of other variables.[5]
Define stratification variables and decide the number of strata to be created. The criteria for defining variables for stratification include age, socioeconomic status, nationality, race, education level and others and should be in line with the research objective. Ideally, the number of 4-6strata should be employed, as any increase in stratification variables will raise the probability for some of them to cancel out the impact of other variables.
定义分层变量并决定要创建的分层数量。确定分层变量的标准包括年龄、社会经济地位、国籍、种族、教育程度等,并应与研究目标相一致。理想情况下,应该使用4-6个阶层的数量,因为任何分层变量的增加将提高其中一些变量抵消其他变量的影响的概率。
- Use a sampling frame to evaluate all the elements in the target population. Make changes afterwards based on coverage and grouping.
- List all the elements and consider the sampling result. Each stratum should be mutually exclusive and add up to cover all members of the population, whilst each member of the population should fall into unique stratum, along with other members with minimum differences.[4]
The number of subgroups can be calculated by multiplying the number of strata for each factor. Factors are measured before or at the time of randomization and experimental subjects are divided into several subgroups or strata according to the results of measurements.
子群的数目可以用每个因素的阶层数目相乘来计算。因子在随机化之前或之时被测量,实验对象根据测量结果被分成若干子群或阶层。
- Make decisions over the random sampling selection criteria. This can be done manually or with a designed computer program.
- Assign a random and unique number to all the elements followed by sorting these elements according to their number assigned.
Within each stratum, several randomization strategies can be applied, which involves simple randomization, blocked randomization, and minimization.
在每个地层中,可以采用多种随机化策略,包括简单的随机化、阻塞随机化和最小化。
- Review the size of each stratum and numerical distribution of all elements in every strata. Determine the type of sampling, either proportional or disproportional stratified sampling.
- Carry out the selected random sampling as defined in step 5. At minimum, one element must be chosen from each stratum so that the final sample includes representatives from every stratum. If two or more elements from each stratum are selected, error margins of the collected data can be calculated.[5]
Simple randomization is considered as the easiest method for allocating subjects in each stratum. Subjects are assigned to each group purely randomly for every assignment. Even though it is easy to conduct, simple randomization is commonly applied in strata that contain more than 100 samples since a small sampling size would make assignment unequal.
简单随机化被认为是最简单的方法分配主体在每个阶层。每次分配的主题都是随机分配给每个小组的。尽管简单的随机化方法易于实施,但是由于小样本容易造成分配不等,因此在样本数超过100个的地层中常常采用简单的随机化方法。
Techniques
Block randomization is commonly used in the experiment with a relatively big sampling size to avoid the imbalance allocation of samples with important characteristics. In certain fields with strict requests of randomization such as clinical trials, the allocation would be predictable when there is no blinding process for conductors and the block size is limited. The blocks permuted randomization in strata could possibly cause an imbalance of samples among strata as the number of strata increases and the sample size is limited, For instance, there is a possibility that no sample is found meeting the characteristic of certain strata.
为了避免重要特征样本分配不平衡的问题,实验中常采用分块随机化的方法,采样规模较大。在某些严格要求随机化的领域,例如临床试验,当没有导体的盲法和块大小有限时,分配是可以预测的。随着地层数量的增加和样本容量的限制,地层中的块体随机化可能导致地层之间样本的不平衡,例如,有可能找不到符合特定地层特征的样本。
Stratified randomization decides one or multiple prognostic factors to make subgroups, on average, have similar entry characteristics. The patient factor can be accurately decided by examining the outcome in previous studies.[6]
The number of subgroups can be calculated by multiplying the number of strata for each factor. Factors are measured before or at the time of randomization and experimental subjects are divided into several subgroups or strata according to the results of measurements.[7]
In order to guarantee the similarity of each treatment group, the "minimization" method attempts are made, which is more direct than random permuted block within strats. In the minimization method, samples in each stratum are assigned to treatment groups based on the sum of samples in each treatment group, which makes the number of subjects keep balance among the group.
为了保证每个处理组之间的相似性,尝试了“最小化”方法,这种方法比层内随机置乱更直接。在最小化方法中,根据每个处理组的样本总和,将每个地层的样本分配给处理组,使处理组的受试者人数保持平衡。
Within each stratum, several randomization strategies can be applied, which involves simple randomization, blocked randomization, and minimization.
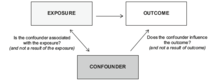
Confounding factors are important to consider in clinical trials
在临床试验中,混杂因素是需要考虑的重要因素
Simple randomization within strata
Stratified random sampling is useful and productive in situations requiring different weightings on specific strata. In this way, the researchers can manipulate the selection mechanisms from each strata to amplify or minimize the desired characteristics in the survey result.
分层随机抽样在特定地层需要不同权重的情况下是有用的和有效的。通过这种方式,研究人员可以操纵来自每个阶层的选择机制,以便在调查结果中放大或减少所需的特征。
Simple randomization is considered as the easiest method for allocating subjects in each stratum. Subjects are assigned to each group purely randomly for every assignment. Even though it is easy to conduct, simple randomization is commonly applied in strata that contain more than 100 samples since a small sampling size would make assignment unequal.[7]
Stratified randomization is helpful when researchers intend to seek for associations between two or more strata, as simple random sampling causes a larger chance of unequal representation of target groups. It is also useful when the researchers wish to eliminate confounders in observational studies as stratified random sampling allows the adjustments of covariances and the p-values for more accurate results.
当研究人员试图寻找两个或多个阶层之间的联系时,分层随机化是有帮助的,因为简单的随机抽样会导致目标群体代表性不平等的可能性更大。当研究人员希望在观察研究中消除混杂因素时,这也是有用的,因为分层随机抽样允许调整协方差和 p 值以获得更准确的结果。
Block randomization within strata
Block randomization, sometimes called permuted block randomization, applies blocks to allocate subjects from the same strata equally to each group in the study. In block randomization, allocation ratio (ratio of the number of one specific group over other groups) and group sizes are specified. The block size must be the multiples of the number of treatments so that samples in each stratum can be assigned to treatment groups with the intended ratio.[7] For instance, there should be 4 or 8 strata in a clinical trial concerning breast cancer where age and nodal statuses are two prognostic factors and each factor is split into two-level. The different blocks can be assigned to samples in multiple ways including random list and computer programming.[8][9]
There is also a higher level of statistical accuracy for stratified random sampling compared with simple random sampling, due to the high relevance of elements chosen to represent the population. The step of stratified randomization is extremely important as an attempt to ensure that no bias, delibrate or accidental, affects the representative nature of the patient sample under study. It increases the study power, especially in small clinical trials(n<400), as these known clinical traits stratified are thought to effect the outcomes of the interventions. It helps prevent the occurrence of type I error, which is valued highly in clinical studies. It also has an important effect on sample size for active control equivalence trials and in theory, facilitates subgroup analysis and interim analysis.
与简单随机抽样相比,分层随机抽样具有更高的统计准确性,因为所选择的元素代表总体具有高度的相关性。分层随机化的步骤是非常重要的,它试图确保没有偏差,取样或偶然,影响研究中患者样本的代表性。它增加了研究力量,特别是在小型临床试验(n < 400) ,因为这些已知的临床特征分层被认为影响干预的结果。它有助于防止 i 型错误的发生,这在临床研究中是很有价值的。它还对主动控制等效试验的样本容量有重要影响,并在理论上简化了亚组分析和中期分析。
The subgroup size is taken to be of the same importance if the data available cannot represent overall subgroup population. In some applications, subgroup size is decided with reference to the amount of data available instead of scaling sample sizes to subgroup size, which would introduce bias in the effects of factors. In some cases that data needs to be stratified by variances, subgroup variances differ significantly, making each subgroup sampling size proportional to the overall subgroup population cannot be guaranteed.
如果可用的数据不能代表整个分组人口,则子组大小被认为具有同样的重要性。在一些应用中,子群大小是根据可用数据量来决定的,而不是按照子群大小来衡量样本大小,这会在因素的影响中引入偏倚。在某些情况下,数据需要由方差分层,分组方差差异显著,使得每个分组抽样大小与整个分组总体成比例不能得到保证。
Block randomization is commonly used in the experiment with a relatively big sampling size to avoid the imbalance allocation of samples with important characteristics. In certain fields with strict requests of randomization such as clinical trials, the allocation would be predictable when there is no blinding process for conductors and the block size is limited. The blocks permuted randomization in strata could possibly cause an imbalance of samples among strata as the number of strata increases and the sample size is limited, For instance, there is a possibility that no sample is found meeting the characteristic of certain strata.[10]
Stratified sampling can not be applied if the population cannot be completely assigned into strata, which would result in sample sizes proportional to sample available instead of overall subgroup population.
如果总体不能完全分配到地层中,那么分层抽样就不能应用,这将导致样本大小与可用样本成比例,而不是整个子群总体。
The process of assigning samples into subgroups could involve overlapping if subjects meet the inclusion standard of multiple strata, which could result in a misrepresentation of the population.
如果受试者符合多个阶层的包含标准,将样本分配到各个子群组的过程可能会涉及重叠,这可能会导致人口的不正当手法引诱。
Minimization method
In order to guarantee the similarity of each treatment group, the "minimization" method attempts are made, which is more direct than random permuted block within strats. In the minimization method, samples in each stratum are assigned to treatment groups based on the sum of samples in each treatment group, which makes the number of subjects keep balance among the group.[7] If the sums for multiple treatment groups are the same, simple randomization would be conducted to assign the treatment. In practice, the minimization method needs to follow a daily record of treatment assignments by prognostic factors, which can be done effectively by using a set of index cards to record. The minimization method effectively avoids imbalance among groups but involves less random process than block randomization because the random process is only conducted when the treatment sums are the same. A feasible solution is to apply an additional random list which makes the treatment groups with a smaller sum of marginal totals possess a higher chance (e.g.¾) while other treatments have a lower chance(e.g.¼ ).[11]
Application
Stratified random sampling is useful and productive in situations requiring different weightings on specific strata. In this way, the researchers can manipulate the selection mechanisms from each strata to amplify or minimize the desired characteristics in the survey result.[12]
Stratified randomization is helpful when researchers intend to seek for associations between two or more strata, as simple random sampling causes a larger chance of unequal representation of target groups. It is also useful when the researchers wish to eliminate confounders in observational studies as stratified random sampling allows the adjustments of covariances and the p-values for more accurate results.[13]
There is also a higher level of statistical accuracy for stratified random sampling compared with simple random sampling, due to the high relevance of elements chosen to represent the population.[5] The differences within the strata is much less compared to the one between strata. Hence, as the between-sample differences are minimized, the standard deviation will be consequently tightened, resulting in higher degree of accuracy and small error in the final results. This effectively reduces the sample size needed and increases cost-effectiveness of sampling when research funding is tight.
In real life, stratified random sampling can be applied to results of election polling, investigations into income disparities among social groups, or measurements of education opportunities across nations.[1]
Stratified randomization in clinical trials
In clinical trials, patients are stratified according to their social and individual backgrounds, or any factor that are relevant to the study, to match each of these groups within the entire patient population. The aim of such is to create a balance of clinical/prognostic factor as the trials would not produce valid results if the study design is not balanced.[14] The step of stratified randomization is extremely important as an attempt to ensure that no bias, delibrate or accidental, affects the representative nature of the patient sample under study.[15] It increases the study power, especially in small clinical trials(n<400), as these known clinical traits stratified are thought to effect the outcomes of the interventions.[16] It helps prevent the occurrence of type I error, which is valued highly in clinical studies.[17] It also has an important effect on sample size for active control equivalence trials and in theory, facilitates subgroup analysis and interim analysis.[17]
Category:Sampling (statistics)
类别: 抽样(统计)
Advantage
Category:Sampling techniques
类别: 抽样技术
This page was moved from wikipedia:en:Stratified randomization. Its edit history can be viewed at 分层随机试验/edithistory
- ↑ 1.0 1.1 1.2 1.3 Nickolas, Steven (July 14, 2019). "How Stratified Random Sampling Works". Investopedia (in English). Retrieved 2020-04-07.
- ↑ "Simple random sample", Wikipedia (in English), 2020-03-18, retrieved 2020-04-07
- ↑ "Stratified sampling", Wikipedia (in English), 2020-02-09, retrieved 2020-04-07
- ↑ 4.0 4.1 Stephanie (Dec 11, 2013). "Stratified Random Sample: Definition, Examples". Statistics How To (in English). Retrieved 2020-04-07.
- ↑ 5.0 5.1 5.2 5.3 "Stratified Random Sampling: Definition, Method and Examples". QuestionPro (in English). 2018-03-13. Retrieved 2020-04-07.
- ↑ Sylvester, Richard (December 1982). "Fundamentals of clinical trials". Controlled Clinical Trials. 3 (4): 385–386. doi:10.1016/0197-2456(82)90029-0. ISSN 0197-2456.
- ↑ 7.0 7.1 7.2 7.3 Pocock, Stuart J. (Jul 1, 2013). Clinical trials : a practical approach. Chichester: John Wiley & Sons Ltd. ISBN 978-1-118-79391-6. OCLC 894581169.
- ↑ "Sealed Envelope | Random permuted blocks". www.sealedenvelope.com. Feb 25, 2020. Retrieved 2020-04-07.
- ↑ Friedman, Lawrence M.; Furberg, Curt D.; DeMets, David L. (2010), "Introduction to Clinical Trials", Fundamentals of Clinical Trials, Springer New York, pp. 1–18, doi:10.1007/978-1-4419-1586-3_1, ISBN 978-1-4419-1585-6
- ↑ Fundamentals of clinical trials. Friedman, Lawrence M., 1942-, Furberg, Curt,, DeMets, David L., 1944-, Reboussin, David,, Granger, Christopher B. (Fifth ed.). New York. 27 August 2015. ISBN 978-3-319-18539-2. OCLC 919463985.
- ↑ Pocock, S. J. (March 1979). "Allocation of Patients to Treatment in Clinical Trials". Biometrics. 35 (1): 183–197. doi:10.2307/2529944. ISSN 0006-341X. JSTOR 2529944. PMID 497334.
- ↑ Crossman, Ashley (Jan 27, 2020). "Understanding Stratified Samples and How to Make Them". ThoughtCo (in English). Retrieved 2020-04-07.
- ↑ Hennekens, Charles H. (1987). Epidemiology in medicine. Buring, Julie E., Mayrent, Sherry L. (1st ed.). Boston, Massachusetts: Little, Brown. ISBN 0-316-35636-0. OCLC 16890223.
- ↑ Polit, DF; Beck, CT (2012). Nursing Research: Generating and Assessing Evidence for Nursing Practice, 9th ed.. Philadelphia, USA: Wolters Klower Health: Lippincott Williams & Wilkins..
- ↑ "Patient Stratification in Clinical Trials". Omixon | NGS for HLA (in English). 2014-12-01. Retrieved 2020-04-26.
- ↑ Stephanie (2016-05-20). "Stratified Randomization in Clinical Trials". Statistics How To (in English). Retrieved 2020-04-26.
- ↑ 17.0 17.1 Kernan, W (Jan 1999). "Stratified Randomization for Clinical Trials". Journal of Clinical Epidemiology. 52 (1): 19–26. doi:10.1016/S0895-4356(98)00138-3. PMID 9973070.