“有向无环图”的版本间的差异
| 第97行: | 第97行: | ||
<math>B</math>的''k''次方记为<math>B^k=(b_{ij}^k)_{d*d}</math>,其中 | <math>B</math>的''k''次方记为<math>B^k=(b_{ij}^k)_{d*d}</math>,其中 | ||
| − | :<math>b_{ij}^k=\sum _{h=1}^ | + | :<math>b_{ij}^k=\sum _{h=1}^d b_{ih}^{k-1}b_{hj}</math> |
<math>b_{ih}*b_{hj}\neq 0</math>当且仅当<math>b_{ih}\neq 0</math>和<math>b_{hj}\neq 0</math>,即从节点<math>v_i</math>到<math>v_h</math>和从<math>v_h</math>到<math>v_j</math>都有路径相通,所以<math>b_{ij}^2</math>的值表示从<math>v_i</math>出发两步到达<math>v_j</math>的路径数量。同理可知,<math>b_{ij}^k</math>表示从 | <math>b_{ih}*b_{hj}\neq 0</math>当且仅当<math>b_{ih}\neq 0</math>和<math>b_{hj}\neq 0</math>,即从节点<math>v_i</math>到<math>v_h</math>和从<math>v_h</math>到<math>v_j</math>都有路径相通,所以<math>b_{ij}^2</math>的值表示从<math>v_i</math>出发两步到达<math>v_j</math>的路径数量。同理可知,<math>b_{ij}^k</math>表示从 | ||
<math>v_i</math>出发经<math>k</math>步到达<math>v_j</math>的路径数量。<math>b_{ij}^k=0</math>表示不存在这样的路径。 | <math>v_i</math>出发经<math>k</math>步到达<math>v_j</math>的路径数量。<math>b_{ij}^k=0</math>表示不存在这样的路径。 | ||
2021年6月21日 (一) 20:23的版本
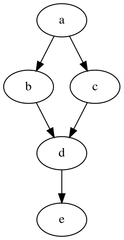
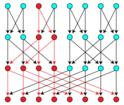
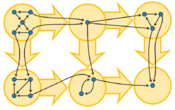
在图论和计算机科学中,有向无环图 Directed acyclic graph(DAG 或 dag)是一个没有定向循环的有向图。也就是说,它由 顶点 Vertex 和 边 Edge (也称为弧)组成,每条边都从一个顶点指向另一个顶点,沿着这些顶点的方向 不会形成一个闭合的 环 Loop 。有向图是一个有向无环图当且仅当它可以通过将顶点按照与所有边方向一致的线性顺序排列构成 拓扑排序 Topologically ordered 。有向无环图有许多科学的和计算的应用,从生物学(进化论,家谱,流行病学)到社会学(引文网络)到计算(调度)。
定义
图是由顶点和连接顶点对的边组成的,顶点可以是任何一种由边成对连接的对象。在有向图中,每条边都有一个方向,从一个顶点到另一个顶点。
有向图中的 路径 Path 是不重复的顶点[math]\displaystyle{ i_1,…,i_m }[/math](至少2个)的序列,满足对于所有的[math]\displaystyle{ k=1,…,{m−1} }[/math]存在边在顶点[math]\displaystyle{ i_k }[/math]和顶点[math]\displaystyle{ i_{k+1} }[/math]之间; 如果一条路的第一条边的起始顶点与它的最后一条边的结束顶点相同,那么它就形成了一个环。有向无环图即为没有环出现的有向图。[1][2][3]
当存在一条从顶点u到顶点v的路径时,顶点v被称作是从顶点u 可达的 Reachability 。每个顶点都是从自身可达的(通过一条没有边的路径)。如果一个顶点可以从一条 非平凡路径(一条由一个或更多边组成的路径)到达自身,那么这条路径就是一个环。因此,有向无环图也可以被定义为没有顶点可以通过非平凡路径到达自身的图。[4]
数学性质
可达性,传递闭包和传递归约
有向无环图的 可达性 Reachability 可以用其顶点的 偏序关系 Partial order ≤来表示。在偏序关系中,如果存在一条路径从顶点u指向顶点v,它们的偏序关系可被写作u ≤ v。这也被称作v是从u可达的。[5]不同的有向无环图可以有着相同的可达关系和偏序关系。[6]例如,有两条边a → b,b → c的有向无环图,和有三条边的a → b, b → c,a → c的有向无环图有着相同的偏序关系a ≤ b ≤ c。
对于一个有向无环图G,它的 传递闭包 Transitive closure 等同于一个在保持与其相同可达性的情况下,边数最多的图。在这个图中,当u可达v的时候,边u → v必定存在。换句话说,每个G中的非相同元素偏序关系对u ≤ v都在这个图中有一条边。这可以被视作用图来可视化图G的可达性关系。
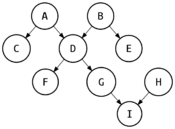
有向无环图G的 传递规约 Transitive reduction 为和其有着相同可达性,边数最少的图。它是G的一个子图。构造方法为当G有着一条更长的路径连接顶点u和v的时候,消去边u → v。
传递约简和传递闭包都是有向无环图的特有概念。相反的,对于有向有环图,可以存在多个与原图有着相同可达性的最简子图。[7]
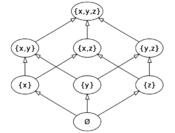
对于有向无环图G和表达其可达性的偏序关系≤,它的传递规约也可以看作包含G的 覆盖关系 Covering relation 中每一条边的G的子图。传递规约在图示有向无环图的偏序关系时十分有用,因为它们比其他具有相同偏序关系的图的边数要少,这简化了绘图。偏序关系的 哈斯图 Hasse diagram 由将传递规约中的每条边的起点绘制在其终点的下方而得到。[8]
拓扑排序
有向无环图的 拓扑排序 Topological ordering 为所有边的起点都出现在其终点之前的排序。能构成拓扑排序的图一定没有环,因为环中的一条边必定从排序较后的顶点指向比其排序更前的顶点。[2]基于此,拓扑排序可以被用来定义有向无环图:当且仅当一个有向图有拓扑排序,它是有向无环图。一般情况下,拓扑排序并非唯一。有向无环图仅仅在存在一条路径可以包含其所有顶点的情况下,有唯一的拓扑排序方式,这时,拓扑排序与它们在这条路径中出现的顺序相同。[9]
有向无环图的拓扑排序族等同于其可达性的 线性拓展 Linear extension 族。 [10]因此,偏序关系相同的任意两个图会有相同的拓扑排序集。
组合计数
罗宾逊 Robinson (1973) 研究了有向无环图的 图计数 Graph enumeration 问题。[11] 如标号顶点在拓扑排序中出现的顺序不受限制,有n个顶点的标号有向无环图的数量为
- 1, 1, 3, 25, 543, 29281, 3781503, … (OEIS中的数列A003024)。
其中n = 0, 1, 2, 3,……。这个数列的 递推关系式 Recurrence relation 是
- [math]\displaystyle{ a_n = \sum_{k=1}^n (-1)^{k-1} {n\choose k}2^{k(n-k)} a_{n-k}. }[/math][11]
埃里克·韦斯坦因 Eric W. Weisstein [12],n个顶点的标号有向无环图的数量与其中所有 特征值 Eigenvalues 都为正实数的n*n 逻辑矩阵 的数量相同。这一点随后被 McKay 证实,证明采用了 双射法 Bijective:一个矩阵A是有向无环图的一个 邻接矩阵 Adjacency matrix ,当且仅当A + I是一个所有特征值都为正数的逻辑矩阵,其中I为 单位矩阵 Identity matrix 。因为一个有向无环图不允许 自环 Self-loops ,它的邻接矩阵的对角线必定全为0。因此,加上I保持了所有矩阵因子都是0或1的特性。[13]
相关概念
多重树 Polytree 由将自由树的边 定向 Orienting 而得到。[14] 多重树必定是有向无环图。对于有根树,将其所有边赋予指离根的方向也可以得到有向无环图,即 树状图 。
强明确树 Multitree 是每两个顶点最多被一条路径所连接的有向无环图。等价的说,它是满足以下性质的一个有向无环图:对于图中每个顶点v,从v可达的顶点组成一颗树。[15]
相关计算问题
基于邻接矩阵的有向无环图的判别方法
定理: 对于邻接矩阵 [math]\displaystyle{ B\in \left\{ 0, 1 \right\}^{d*d} }[/math], [math]\displaystyle{ B }[/math]是有向无环图当且仅当
- [math]\displaystyle{ tr(e^B)=d }[/math]
依据泰勒展开公式 [math]\displaystyle{ e^B=I+\sum_{k=1}^{\infty}\,\frac{1}{k!}B^k }[/math],有
- [math]\displaystyle{ tr(I+\sum_{k=1}^{\infty}\,\frac{1}{k!}B^k)-d=0 }[/math]
其中, [math]\displaystyle{ B_{ij}^k }[/math]是从[math]\displaystyle{ i }[/math]到[math]\displaystyle{ j }[/math]的长度为[math]\displaystyle{ k }[/math]的有向路径的数量,例如
- [math]\displaystyle{ B_{ij}^2=\sum_kB_{ik}B_{kj} }[/math]
基于邻接矩阵判断有向图有没有环
对于有向图[math]\displaystyle{ G=(V,E) }[/math],构造[math]\displaystyle{ d=\mid V \mid }[/math]阶方阵[math]\displaystyle{ B=(b_{ij})_{d*d} }[/math],其中
- [math]\displaystyle{ b_{ij}=\mid e_k \mid,e_k=(v_i,v_j)\in E }[/math]
称矩阵[math]\displaystyle{ B }[/math]为有向图[math]\displaystyle{ G }[/math]的节点邻接矩阵。
[math]\displaystyle{ B }[/math]的k次方记为[math]\displaystyle{ B^k=(b_{ij}^k)_{d*d} }[/math],其中
- [math]\displaystyle{ b_{ij}^k=\sum _{h=1}^d b_{ih}^{k-1}b_{hj} }[/math]
[math]\displaystyle{ b_{ih}*b_{hj}\neq 0 }[/math]当且仅当[math]\displaystyle{ b_{ih}\neq 0 }[/math]和[math]\displaystyle{ b_{hj}\neq 0 }[/math],即从节点[math]\displaystyle{ v_i }[/math]到[math]\displaystyle{ v_h }[/math]和从[math]\displaystyle{ v_h }[/math]到[math]\displaystyle{ v_j }[/math]都有路径相通,所以[math]\displaystyle{ b_{ij}^2 }[/math]的值表示从[math]\displaystyle{ v_i }[/math]出发两步到达[math]\displaystyle{ v_j }[/math]的路径数量。同理可知,[math]\displaystyle{ b_{ij}^k }[/math]表示从 [math]\displaystyle{ v_i }[/math]出发经[math]\displaystyle{ k }[/math]步到达[math]\displaystyle{ v_j }[/math]的路径数量。[math]\displaystyle{ b_{ij}^k=0 }[/math]表示不存在这样的路径。
拓扑排序和识别
可以用 线性时间复杂度 的卡恩算法来找到一个有向无环图的拓扑排序。[16]简单来说,开设一个存放结果的列表L,先将入度为零的节点放到L中,因为这些节点没有任何的父节点。将与这些节点相连的边从图中去掉,再寻找图中入度为零的节点。对于新找到的节点来说,他们的父节点已经都在L中了,所以也可以从末端插入L。重复上述操作,直到找不到入度为零的节点。[17] 另外一种构造拓扑排序的算法是将 深度优先搜索 的 后序遍历 结果翻转。[16]
检查一个有向图是否为有向无环图亦可在线性时间内完成。一种方法是先找到一个拓扑排序,然后测试这个排序是否能符合图中每条边所连顶点在排序中应该出现的顺序。[18] 对于卡恩算法在内的部分拓扑排序算法,通过在算法终止时判断是否满足一定条件即可知道图是否有环。[17]如果有环,卡恩算法最终获得的L中节点个数会与图的节点总数不同。
从其他图构建
任意无向图都可以被转化为有向无环图。构造方法是选定一个顶点的 全序关系 Total order ,并将无向图中所有边从全序关系中较前的顶点指向较后的顶点。这种方法是定向方法中的 无环定向 Acyclic orientation 。不同的全序关系可能推出相同的无环定向,因此一个包含n个顶点的图的无环定向数量小于n!。如果定义χ为给定图的 色多项式 Chromatic polynomial ,无环定向数量等于|χ(−1)|。[19]
任意有环有向图都可以被转化为有向无环图。只要从图中移除 反馈节点集 Feedback vertex set 或 反馈边集 Feedback arc set ,即对于图中每个环,至少包括环中一个顶点或边的集合。不过,找到反馈节点或边的最小集合是 NP困难 NP-hard 问题。[20] 另外一种方法将有环有向图去环的方法是将每个强连通分量收缩为一个顶点。[21] 对于无环图,它的最小反馈顶点或边集为 空集 ,它的强连通分量则为自身。
传递闭包和传递约简
有向无环图的传递闭包可以通过 广度优先搜索 或 深度优先搜索 对每个节点测试可达性来构建。算法对于一个有着n个顶点和m条边的有向无环图的复杂度为O(mn)。[22]也可以使用 矩阵乘法算法 Matrix multiplication algorithm 中最快的 Coppersmith–Winograd算法,其复杂度为O(n2.3728639)。这个算法理论上在 稠密图 Dense graph中快过O(mn)。[23]
不论在哪种传递闭包算法中,那些被一条长度至少为2的路径所连接的顶点对,都可以和只有一条长度为1的路径所连接的顶点对区分开。由于传递约简包含后者,传递约简可以在和传递闭包相同的 渐进时间复杂度 Asymptotic computational complexity 中被构建。[24]
闭包问题
闭包是一个图中没有出边的顶点子集,即不存在从子集中顶点指向子集外顶点的边。 闭包问题 Closure problem 是则是找到带权图中使得权之和最大或最小的子集。闭包问题可以看作 最大流问题 的简化版,在 多项式时间 内被解决。实际上,是否有环对于找到闭包没有影响。[25]
最短或最长路径问题
基于拓扑排序的性质,有向无环图的最短路问题 Shortest paths和最长路径问题 Longest paths可以在线性时间内解决。将顶点拓扑排序后,从前到后遍历每一个顶点,对于遍历到的顶点,更新其所有出边所到达顶点的长度值。如果求最短路,则在本边是更短路径的一部分时更新。求最长路则反之。[26]对于非有向无环图,最短路需要用复杂度为[math]\displaystyle{ O(|E|+|V|\log|V|) }[/math]的 戴克斯特拉算法 Dijkstra's algorithm 或[math]\displaystyle{ O (|V| |E|) }[/math]的 贝尔曼-福特算法 Bellman–Ford algorithm 等。[27]最长路径则是一个NP困难问题。[28]
应用
调度
有向无环图的偏序关系可以在调度上有着先后顺序限制的系统任务中发挥作用。[29]调度问题的一个重要种类是串联需要更新的对象,如电子计算表中某个单元格的计算公式依赖于其他单元格,或在程序的源代码被修改后重新编译目标文件。 依赖图 Dependency graph 则记录了这种更新依赖关系。其每个顶点对应一个需要被更新的对象,边则表示更新的关系。依赖图中的环被称为 环状依赖 Circular dependency 。环状依赖通常是不被允许出现的,因为不能保证圈内任务排定顺序的一致性。无环的依赖图即为有向无环图。[30]
举例来说,当电子表格中一个单元格的数值发生改变,其他直接或间接依赖于该单元格的所有单元格的值都需要被重新计算。被调度的任务为重新计算某个特定单元格的值。当一个单元格的值取决于另外一个单元格时,两个单元格之间则有依赖关系。每个被依赖单元格的值的计算过程都必须先于使用它的表达式执行。使用依赖图的拓扑排序来调度任务使得在每个单元格的值都仅被重新计算一次的情况下,整个工作表都能被更新。[31]相似的任务调度场景出现在程序源代码编译的 Makefile ,[31]和优化计算机程序底层执行的指令调度中。[32]

计划评审技术是一种基于有向无环图的计划排定技术,通常用于组织大型的人工项目。在计划评审技术中,每个顶点表示项目的一个里程碑 Milestone(项目管理 project management),每条有向边表示任务或者活动,连接着表示任务开始或结束的两个节点。每条边则被标注上预估需时。图中的最长路径即为项目的关键路径。关键路径决定了项目所需的总时间,里程碑的完成时间取决于结束于本顶点的最长路径。[33]
数据处理网络
有向无环图可以用于表示处理数据的元素网络。在网络中,数据从一个元素顶点的入边进入,处理后从出边离开。
在电子电路设计中,静态组合逻辑电路块可以被表示为由逻辑门组成的有向无环系统。每个逻辑门对输入做一次函数处理,输入和输出均为一个位元组。通常,这些电路块的输出不能够再作为输入,除非它们被存储在寄存器或者状态单元中,以保证图不出现环。[34]
数据式编程 Dataflow programming 语言描述针对 数据流 Data stream 的操作,以及操作的输出和其他操作的输入之间的关系。这类型的语言使得描绘高重复率数据处理任务的变得更加简单,因为同样的数据操作可以应用于许多数据项。数据操作可以用有向无环图来表示。这些数据操作可以被并发执行,从而高效利用多核心处理器。[35]
在编译器中,直线码(不含条件分支和循环的代码段)可以使用有向无环图表示。图标示出每个算术运算的输入和输出。这种表示法让编译器能执行 通用子表达式删除 Common subexpression elimination ,使得代码更高效。[36]
因果结构
用顶点表示事件,边表示因果关系的图通常是无环的。[37]事件由时间上的先后顺序来排列,所有箭头遵循从先发生事件指向后发生事件的原则,因此也不存在环。
举例来说,贝叶斯网络 Bayesian network 表示多个概率事件的关联网络。顶点表示事件,后续事件的发生可能性则可以通过其在有向无环图的前驱节点的发生概率计算出来。[38]在此基础上,一个有向无环图的 端正图 Moral graph 通过以下方法而得到:将单个顶点的所有父节点之间添加一条无向边,再将所有的有向边换成无向边。[39]
另外一种具有相似因果结构的图是 影响图 Influence diagram 。其顶点表示决策或不确定的事件,边表示两个顶点之间的因果关系。[40]在流行病学中,这些表示因果关系的图表常常用来评估不同干预手段的效果。[41][42]
系谱学和版本历史
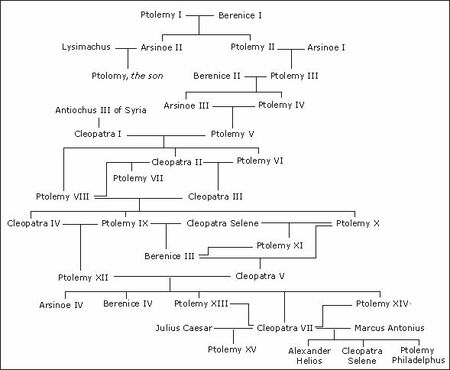
谱系图可以看作是有向无环图,顶点代表家族成员,边代表亲子关系。[43]虽然谱系图也被称作为家族“树”, 但近亲结婚导致的 血统崩溃 Pedigree collapse 会违反树的性质。即一个孩子的祖先既可以从父亲向上追溯,也可以从母亲一侧。[44]图中的母系血统和父系血统则可以看作为树。因为没有人可以是自己的祖先,谱系图是无环的。[45]
基于相同的原因, 一个分散式版本控制系统的版本历史的结构也是有向无环图。在系统中,每个版本对应一个节点。边连接起有直接衍生关系的两个版本。由于分支合并的存在,这个结构并不能用树来表示。[46]
在计算几何领域,许多随机化算法都会维护一个“历史有向无环图”,用以记录结构变动中的旧几何结构。例如,在 德劳内三角化 Delaunay triangulation 的随机增量算法中,在添加每个点时,通过用三个较小的三角形替换一个三角形,以及通过“翻转”操作将三角形对替换为另一对三角形,来改变三角剖分。在该算法的历史有向无环图中,每个在算法中构建出的三角形对应一个顶点,边则将每个三角形和替代它的两个或三个三角形连接起来。这种图结构可以高效地处理 点定位 Point location 问题,即对于一个查询点q,找到它在德勞內三角剖分中的位置。在历史有向无环图中,从起点开始,不断移动到包含q的替代三角形组,最后到达的终点必定代表包含q的德劳内三角形。[47]
引用图
在 引用图 Citation graph 中, 每个顶点代表单篇著作,边代表著作之间的引用关系。1965年普莱斯的文章“科学文献的网络”是使用引用图的一个经典例子。[48]在引用图中,每篇论文的 引用影响(引用次数) Citation impact 为对应顶点的入度。这是引文分析中的一种重要的展示方式。另一个例子是法律裁判中,法官通过引用过往案例中的判决来支持他们的结论。引用图亦可以用来描绘专利,因为专利必须要提及现有技术,即已经公开的并且和本专利有关的先前专利。
相较于网络科学中对一般图的研究,有向无环图的独特性质可以被用来作深层次分析。例如,传递规约可以呈现引用在不同应用领域的分布情况,这突出了不同领域中不同的引用网构造机制。[49]引用图的衍生概念还有 主干道路分析 Main path analysis ,即对引用图中最显著的一条路径的分析。
数据压缩
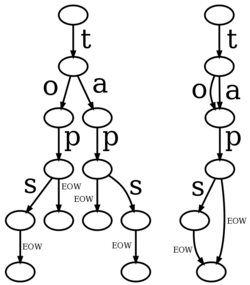
有向无环图也可以用于对一系列序列的压缩中。在这里,有向无环图中的路径代表这些序列。当多个序列有共同的子序列时,子序列可以被表示为这些序列对应路径的公共边。比起直接列出所有序列,这种方法占用更少空间。例如, 无环确定有限状态自动机 Deterministic acyclic finite state automaton 为仅含单个源(入度为0的顶点)的有向无环图,其每条边附有一个或多个字符。每条其源到汇(出度为0的节点)的路径均代表一个字符串,字符串可以是英文单词。[50]与其结构不同但功能相似的树称为trie。相比于trie,有向无环词图允许多条边指向同一个顶点,使得具有相同后缀的一些词的词头可以被相同的顶点所表示,因而更省空间。[51]
二元决策图是基于有向无环图的一种数据结构,用于表示布尔函数[52][53]。在二元决策图中,每个非汇节点对应一个布尔变量,每个汇和边则表示0或1。要找到一个解释的真值,只要从唯一的源顶点出发,沿着该顶点代表的布尔变量的实际真值所对应的出边一直前进,到达的汇则为其真值。如同有向无环词图可以被看作是trie的一种压缩形式一样,二元决策图可以被看作是 决策树 的压缩形式。它通过将导向相同结果的边重新汇合到一个顶点来节省空间。[54]
参考文献
- ↑ Thulasiraman, K.; Swamy, M. N. S. (1992), "5.7 Acyclic Directed Graphs", Graphs: Theory and Algorithms, John Wiley and Son, p. 118, ISBN 978-0-471-51356-8.
- ↑ 2.0 2.1 Bang-Jensen, Jørgen (2008), "2.1 Acyclic Digraphs", Digraphs: Theory, Algorithms and Applications, Springer Monographs in Mathematics (2nd ed.), Springer-Verlag, pp. 32–34, ISBN 978-1-84800-997-4.
- ↑ Christofides, Nicos (1975), Graph theory: an algorithmic approach, Academic Press, pp. 170–174
{{citation}}: Cite has empty unknown parameter:|1=(help). - ↑ Mitrani, I. (1982), Simulation Techniques for Discrete Event Systems, Cambridge Computer Science Texts, vol. 14, Cambridge University Press, p. 27, ISBN 9780521282826.
- ↑ Kozen, Dexter (1992), The Design and Analysis of Algorithms, Monographs in Computer Science, Springer, p. 9, ISBN 978-0-387-97687-7.
- ↑ Banerjee, Utpal (1993), "Exercise 2(c)", Loop Transformations for Restructuring Compilers: The Foundations, Springer, p. 19, ISBN 978-0-7923-9318-4.
- ↑ Bang-Jensen, Jørgen; Gutin, Gregory Z. (2008), "2.3 Transitive Digraphs, Transitive Closures and Reductions", Digraphs: Theory, Algorithms and Applications, Springer Monographs in Mathematics, Springer, pp. 36–39, ISBN 978-1-84800-998-1.
- ↑ Jungnickel, Dieter (2012), Graphs, Networks and Algorithms, Algorithms and Computation in Mathematics, vol. 5, Springer, pp. 92–93, ISBN 978-3-642-32278-5.
- ↑ Sedgewick, Robert; Wayne, Kevin (2011), "4,2,25 Unique topological ordering", Algorithms (4th ed.), Addison-Wesley, pp. 598–599, ISBN 978-0-13-276256-4.
- ↑ Bender, Edward A.; Williamson, S. Gill (2005), "Example 26 (Linear extensions – topological sorts)", A Short Course in Discrete Mathematics, Dover Books on Computer Science, Courier Dover Publications, p. 142, ISBN 978-0-486-43946-4.
- ↑ 11.0 11.1 Robinson, R. W. (1973), "Counting labeled acyclic digraphs", in Harary, F. (ed.), New Directions in the Theory of Graphs, Academic Press, pp. 239–273. See also Harary, Frank; Palmer, Edgar M. (1973), Graphical Enumeration, Academic Press, p. 19, ISBN 978-0-12-324245-7.
- ↑ Weisstein, Eric W. "Weisstein's Conjecture". MathWorld.
- ↑ McKay, B. D.; Royle, G. F.; Wanless, I. M.; Oggier, F. E.; Sloane, N. J. A.; Wilf, H. (2004), "Acyclic digraphs and eigenvalues of (0,1)-matrices", Journal of Integer Sequences, 7, Article 04.3.3.
- ↑ Rebane, George; Pearl, Judea (1987), "The recovery of causal poly-trees from statistical data", in Proc. 3rd Annual Conference on Uncertainty in Artificial Intelligence (UAI 1987), Seattle, WA, USA, July 1987 (PDF), pp. 222–228.
- ↑ Furnas, George W.; Zacks, Jeff (1994), "Multitrees: enriching and reusing hierarchical structure", Proc. SIGCHI conference on Human Factors in Computing Systems (CHI '94), pp. 330–336, doi:10.1145/191666.191778, ISBN 978-0897916509.
- ↑ 16.0 16.1 Section 22.4, Topological sort, pp. 549–552.
- ↑ 17.0 17.1 Jungnickel, Dieter (2012), Graphs, Networks and Algorithms, Algorithms and Computation in Mathematics, 5, Springer, pp. 50–51, ISBN 978-3-642-32278-5.
- ↑ For depth-first search based topological sorting algorithm, this validity check can be interleaved with the topological sorting algorithm itself; see e.g. Skiena, Steven S. (2009), The Algorithm Design Manual, Springer, pp. 179–181, ISBN 978-1-84800-070-4.
- ↑ Stanley, Richard P. (1973), "Acyclic orientations of graphs" (PDF), Discrete Mathematics, 5 (2): 171–178, doi:10.1016/0012-365X(73)90108-8.
- ↑ Garey, Michael R.; Johnson, David S. (1979), "Problems GT7 and GT8", Computers and Intractability: A Guide to the Theory of NP-Completeness, W. H. Freeman, pp. 191–192, ISBN 0-7167-1045-5
- ↑ Harary, Frank; Norman, Robert Z.; Cartwright, Dorwin (1965), Structural Models: An Introduction to the Theory of Directed Graphs, John Wiley & Sons, p. 63.
- ↑ Skiena, Steven S. (2009), The Algorithm Design Manual, Springer, p. 495, ISBN 978-1-84800-070-4.
- ↑ Skiena, Steven S. (2009), The Algorithm Design Manual, Springer, p. 496, ISBN 978-1-84800-070-4.
- ↑ Bang-Jensen, Jørgen; Gutin, Gregory Z. (2008), "2.3 Transitive Digraphs, Transitive Closures and Reductions", Digraphs: Theory, Algorithms and Applications, Springer Monographs in Mathematics, Springer, p. 38, ISBN 978-1-84800-998-1.
- ↑ Picard, Jean-Claude (1976), "Maximal closure of a graph and applications to combinatorial problems", Management Science, 22 (11): 1268–1272, doi:10.1287/mnsc.22.11.1268, MR 0403596.
- ↑ Cormen et al. 2001, Section 24.2, Single-source shortest paths in directed acyclic graphs, pp. 592–595.
- ↑ Cormen et al. 2001, Sections 24.1, The Bellman–Ford algorithm, pp. 588–592, and 24.3, Dijkstra's algorithm, pp. 595–601.
- ↑ Cormen et al. 2001, p. 966.
- ↑ Skiena, Steven S. (2009), The Algorithm Design Manual, Springer, pp. 179–181, ISBN 978-1-84800-070-4..
- ↑ Al-Mutawa, H. A.; Dietrich, J.; Marsland, S.; McCartin, C. (2014), "On the shape of circular dependencies in Java programs", 23rd Australian Software Engineering Conference, IEEE, pp. 48–57, doi:10.1109/ASWEC.2014.15, ISBN 978-1-4799-3149-1.
- ↑ 31.0 31.1 Gross, Jonathan L.; Yellen, Jay; Zhang, Ping (2013), Handbook of Graph Theory (2nd ed.), CRC Press, p. 1181, ISBN 978-1-4398-8018-0.
- ↑ Srikant, Y. N.; Shankar, Priti (2007), The Compiler Design Handbook: Optimizations and Machine Code Generation (2nd ed.), CRC Press, pp. 19–39, ISBN 978-1-4200-4383-9.
- ↑ Wang, John X. (2002), What Every Engineer Should Know About Decision Making Under Uncertainty, CRC Press, p. 160, ISBN 978-0-8247-4373-4.
- ↑ Sapatnekar, Sachin (2004), Timing, Springer, p. 133, ISBN 978-1-4020-7671-8.
- ↑ Dennis, Jack B. (1974), "First version of a data flow procedure language", Programming Symposium, Lecture Notes in Computer Science, vol. 19, pp. 362–376, doi:10.1007/3-540-06859-7_145, ISBN 978-3-540-06859-4.
- ↑ Touati, Sid; de Dinechin, Benoit (2014), Advanced Backend Optimization, John Wiley & Sons, p. 123, ISBN 978-1-118-64894-0.
- ↑ Gopnik, Alison; Schulz, Laura (2007), Causal Learning, Oxford University Press, p. 4, ISBN 978-0-19-803928-0.
- ↑ Shmulevich, Ilya; Dougherty, Edward R. (2010), Probabilistic Boolean Networks: The Modeling and Control of Gene Regulatory Networks, Society for Industrial and Applied Mathematics, p. 58, ISBN 978-0-89871-692-4.
- ↑ Cowell, Robert G.; Dawid, A. Philip; Lauritzen, Steffen L.; Spiegelhalter, David J. (1999), "3.2.1 Moralization", Probabilistic Networks and Expert Systems, Springer, pp. 31–33, ISBN 0-387-98767-3.
- ↑ Dorf, Richard C. (1998), The Technology Management Handbook, CRC Press, p. 9-7, ISBN 978-0-8493-8577-3.
- ↑ Boslaugh, Sarah (2008), Encyclopedia of Epidemiology, Volume 1, SAGE, p. 255, ISBN 978-1-4129-2816-8.
- ↑ Pearl, Judea (1995). "Causal diagrams for empirical research". Biometrika. 82 (4): 669–709. doi:10.1093/biomet/82.4.669.
- ↑ Kirkpatrick, Bonnie B. (April 2011), "Haplotypes versus genotypes on pedigrees", Algorithms for Molecular Biology, 6 (10): 10, doi:10.1186/1748-7188-6-10, PMC 3102622, PMID 21504603.
- ↑ McGuffin, M. J.; Balakrishnan, R. (2005), "Interactive visualization of genealogical graphs" (PDF), IEEE Symposium on Information Visualization (INFOVIS 2005), pp. 16–23, doi:10.1109/INFVIS.2005.1532124, ISBN 978-0-7803-9464-3.
- ↑ Bender, Michael A.; Pemmasani, Giridhar; Skiena, Steven; Sumazin, Pavel (2001), "Finding least common ancestors in directed acyclic graphs", Proceedings of the Twelfth Annual ACM-SIAM Symposium on Discrete Algorithms (SODA '01), Philadelphia, PA, USA: Society for Industrial and Applied Mathematics, pp. 845–854, ISBN 978-0-89871-490-6.
- ↑ Bartlang, Udo (2010), Architecture and Methods for Flexible Content Management in Peer-to-Peer Systems, Springer, p. 59, ISBN 978-3-8348-9645-2.
- ↑ Pach, János; Sharir, Micha, Combinatorial Geometry and Its Algorithmic Applications: The Alcalá Lectures, Mathematical surveys and monographs, vol. 152, American Mathematical Society, pp. 93–94, ISBN 978-0-8218-7533-9.
- ↑ Price, Derek J. de Solla (July 30, 1965), "Networks of Scientific Papers" (PDF), Science, 149 (3683): 510–515, Bibcode:1965Sci...149..510D, doi:10.1126/science.149.3683.510, PMID 14325149.
- ↑ Clough, James R.; Gollings, Jamie; Loach, Tamar V.; Evans, Tim S. (2015), "Transitive reduction of citation networks", Journal of Complex Networks, 3 (2): 189–203, arXiv:1310.8224, doi:10.1093/comnet/cnu039.
- ↑ Crochemore, Maxime; Vérin, Renaud (1997), "Direct construction of compact directed acyclic word graphs", Combinatorial Pattern Matching, Lecture Notes in Computer Science, vol. 1264, Springer, pp. 116–129, CiteSeerX 10.1.1.53.6273, doi:10.1007/3-540-63220-4_55, ISBN 978-3-540-63220-7.
- ↑ Lothaire, M. (2005), Applied Combinatorics on Words, Encyclopedia of Mathematics and its Applications, vol. 105, Cambridge University Press, p. 18, ISBN 9780521848022.
- ↑ Lee, C. Y. (1959), "Representation of switching circuits by binary-decision programs", Bell System Technical Journal, 38 (4): 985–999, doi:10.1002/j.1538-7305.1959.tb01585.x.
- ↑ Akers, Sheldon B. (1978), "Binary decision diagrams", IEEE Transactions on Computers, C-27 (6): 509–516, doi:10.1109/TC.1978.1675141.
- ↑ Friedman, S. J.; Supowit, K. J. (1987), "Finding the optimal variable ordering for binary decision diagrams", Proc. 24th ACM/IEEE Design Automation Conference (DAC '87), New York, NY, USA: ACM, pp. 348–356, doi:10.1145/37888.37941, ISBN 978-0-8186-0781-3.
编者推荐
集智课程
巴拉巴西网络科学(课程)
本课程中,有幸邀请了汪小帆、赵海兴、许小可、史定华、陈清华、张江、狄增如、陈关荣、樊瑛、刘宗华这十个来自六大不同高校、在网络科学领域耕耘许久的教授作为导师,依据教材框架,各有侧重地为我们共同勾勒出整个学科的美丽图景,展示这个学科的迷人魅力,指引这个学科的灿烂未来。
知识图谱概述
知识图谱是人工智能的一大技术驱动力,它能够广泛地应用于不同的任务。相比深度学习,知识图谱中的知识可以沉淀,可解释性非常强,类似于人类的思考。近年来,不管是学术界还是工业界都纷纷构建自家的知识图谱,有面向全领域的知识图谱,也有面向垂直领域的知识图谱。其实早在文艺复兴时期,培根就提出了“知识就是力量”,在当今人工智能时代,各大科技公司更是纷纷提出:知识图谱就是人工智能的基础。
相关书籍
《图论导论》
Douglas B.West教授是伊利诺伊大学数学系的资深教授,长期从事图论理论和组合优化方面的研究工作,发表了100多篇论文。本书旨在介绍图论的基本概念、基本定理和算法,帮助读者理解并掌握图的结构和解决图论问题的技巧。另外,本书包含很多图论的新研究结果,并介绍了一些悬而未决的图论问题.证明与应用并举是本书的一个重要特点。
《图论及其应用》
该书籍主要介绍了图论的基本知识、相关定理等,并对于不同图,给出实际应用,如与对集有关的人员分派问题、与Hamilton图有关的旅行售货员问题等,通俗易懂。
本中文词条由孙钦贵翻译,张天健审校,薄荷编辑,欢迎在讨论页面留言。
本词条内容翻译自 wikipedia.org,遵守 CC3.0协议。