“前门调整”的版本间的差异
跳到导航
跳到搜索
| 第26行: | 第26行: | ||
==例子:吸烟与肺癌== | ==例子:吸烟与肺癌== | ||
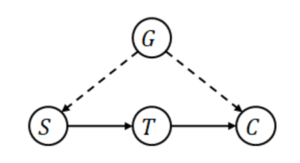
| − | [[文件:吸烟与肺癌.png|缩略图|吸烟与肺癌。S=smoking= | + | [[文件:吸烟与肺癌.png|缩略图|吸烟与肺癌。S=smoking=吸烟(对应表中X),T=Tar=焦油(对应表中Z),C=cancer=肺癌(对应表中Y),G=gene=基因。我们需要估计吸烟对肺癌的因果效应。]] |
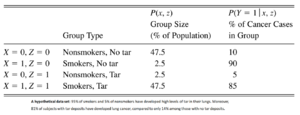
[[文件:吸烟肺癌数据.png|缩略图|吸烟、焦油、肺癌数据。]] | [[文件:吸烟肺癌数据.png|缩略图|吸烟、焦油、肺癌数据。]] | ||
{| class="wikitable" | {| class="wikitable" | ||
| 第55行: | 第55行: | ||
!85 | !85 | ||
|} | |} | ||
| − | + | 从数据中来看,似乎吸烟对肺癌有显著影响,但是烟草公司会从不同的角度争辩,从而给出不同的答案。若我们只看非吸烟者,体内有焦油可以的患癌率从10%降到了5%;若们只看吸烟者,体内有焦油可以的患癌率从90%降到了85%,可见焦油有防护作用。 | |
| + | |||
| + | |||
| + | 数学上,前门调整可以被运用。 | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
<references /> | <references /> | ||
2021年7月23日 (五) 23:29的版本
调整目的: 因果效应估计
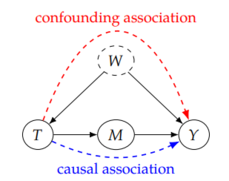
我们期望在给定如下因果图的情况下,判断治疗变量 T 对结果变量 Y 的因果效应 [math]\displaystyle{ P(y|do(t)) }[/math],其中 W 是一个未观测的混淆变量,M 是中介变量。(注意:我们现在观测不到W,无法进行后门调整.。)
主要步骤如下[1]:
- 估计T对M的因果效应[math]\displaystyle{ P(m|do(t)) }[/math] ,由于T-W-Y-M 这条路径被 阻断 (见 D-分离) [math]\displaystyle{ P(m|do(t))=P(m|t) }[/math].
- 估计M对Y的因果效应[math]\displaystyle{ P(y|do(m)) }[/math], 由于 T 阻断了后门路径 M<-T<-W ->Y, 根据后门调整 我们可以轻松得到[math]\displaystyle{ P(y|do(m))= \sum_t P(y|m,t) P(t) }[/math].
- 结合以上两种因果效应[math]\displaystyle{ P(y|do(t))= \sum_m P(y|do(m)) P(m| do(t)) }[/math].
前门准则[2]
定义:我们说变量集 M 关于 T 和 Y 满足前门准则,若:
前门调整
若变量集M关于(T,Y)满足前门准则,并且我们有[math]\displaystyle{ P(t,m)\gt 0 }[/math], T对Y的因果效应是可识别的,
[math]\displaystyle{ P(y|do(t))= \sum_m P(m| t) \sum_{t'} P(y|m,t') P(t') }[/math].
例子:吸烟与肺癌
| 组别 | P(x,z) (每个组别所占百分比) | P(Y=1|x,z) (每组内罹患癌症的百分比) | |
|---|---|---|---|
| X=0,Z=0 | 非吸烟者,肺内无焦油 | 47.5 | 10 |
| X=1,Z=0 | 吸烟者,肺内无焦油 | 2.5 | 90 |
| X=0,Z=1 | 非吸烟者,肺内有焦油 | 2.5 | 5 |
| X=1,Z=1 | 吸烟者,肺内有焦油 | 47.5 | 85 |
从数据中来看,似乎吸烟对肺癌有显著影响,但是烟草公司会从不同的角度争辩,从而给出不同的答案。若我们只看非吸烟者,体内有焦油可以的患癌率从10%降到了5%;若们只看吸烟者,体内有焦油可以的患癌率从90%降到了85%,可见焦油有防护作用。
数学上,前门调整可以被运用。
- ↑ https://www.bradyneal.com/Introduction_to_Causal_Inference-Dec17_2020-Neal.pdf
- ↑ Pearl, Judea. "Models, reasoning and inference." Cambridge, UK: CambridgeUniversityPress 19 (2000).