“克莱伯定律”的版本间的差异
跳到导航
跳到搜索
小 |
|||
| 第1行： | 第1行： | ||
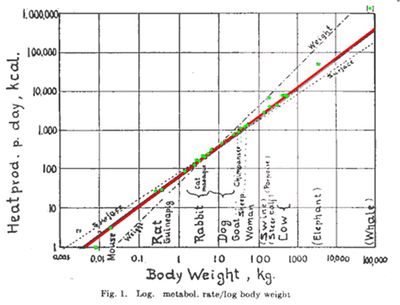
| − | '''克莱伯定律'''（Kleiber's law）<ref>{{cite journal |author=Max Kleiber |title=Body size and metabolism |journal=Hilgardia |volume=6 |pages=315–351 |year=1932}}</ref>根据观测数据提出，对于很多动物，其基础代谢率水平与体重的¾次幂成正比，该定律得名于1930年代早期马克斯·克莱伯(Max Kleiber)的生物学著作。若用符号表示，设''q''<sub>0</sub>为该动物的代谢率，''M''是其重量，则''q''<sub>0</sub> ~ ''M''<sup>¾</sup> | + | '''克莱伯定律'''（Kleiber's law）<ref>{{cite journal |author=Max Kleiber |title=Body size and metabolism |journal=Hilgardia |volume=6 |pages=315–351 |year=1932}}</ref>根据观测数据提出，对于很多动物，其基础代谢率水平与体重的¾次幂成正比，该定律得名于1930年代早期马克斯·克莱伯(Max Kleiber)的生物学著作。若用符号表示，设''q''<sub>0</sub>为该动物的代谢率，''M''是其重量，则''q''<sub>0</sub> ~ ''M''<sup>¾</sup>。因此一般一只猫的重量是一只老鼠的100倍，那么它的代谢量比老鼠约大31倍。而在植物中，指数则接近于1。[[File:Kleiber1947.jpg|right|thumb|400px|'''Figure 1'''. Body size versus metabolic rate for a variety of species<ref>{{cite journal |author=Kleiber M |title=Body size and metabolic rate |journal=Physiological Reviews |volume=27 |issue=4 |pages=511–541 |year=1947 |pmid=20267758 }}</ref>. Originally published in Kleiber (1947).]] |
==定律背后的原因== | ==定律背后的原因== | ||
| − | + | 根据一些学者的研究<ref>{{cite journal|last=West|first=Geoffreyt|title=A General Model for the Origin of Allometric Scaling Laws in Biology|journal=Science|year=1997|volume=276|issue=122}}</ref><ref>{{cite journal|last=Shour|first=Robert|title=Entropy and its relationship to allometry|journal=arXiv|date=November 2012|volume=arXiv:0804.1924|url=http://arxiv.org/abs/0804.1924}}</ref>，克莱伯定律像许多其他的[[异速生长律]]定律一样，是动物循环系统物理学和几何学特性的结果。同一物种中，年轻的个体比年老的个体每份重量的呼吸消耗更多，因为它们体重中中组织结构的比例更大，而储能的比例较小。结构质量需要耗费养护能量，而储能的质量则不需要。 | |
具体来说，West， Enquist和Brown提出三点假设（1）代谢率{{Mvar|B}}正比于循环系统中的营养流量（即体液总流量）{{Mvar|Q}}，即<math>B\propto Q</math>（2）体液（例如血液）总体积{{Mvar|V}}正比于体重{{Mvar|M}}，即<math>V \propto M</math>。这个假设的成立意味着循环系统中的能量耗散降至最低（3）循环系统由微管组成（例如毛细血管、肺泡）。循环系统中的微管尽管千差万别，但总的来说，都具有层级结构，有自相似性。因为通过一个微管的体液流量正比于微管体积，所以微管总数{{Mvar|N}}正比于体液总流量，即 | 具体来说，West， Enquist和Brown提出三点假设（1）代谢率{{Mvar|B}}正比于循环系统中的营养流量（即体液总流量）{{Mvar|Q}}，即<math>B\propto Q</math>（2）体液（例如血液）总体积{{Mvar|V}}正比于体重{{Mvar|M}}，即<math>V \propto M</math>。这个假设的成立意味着循环系统中的能量耗散降至最低（3）循环系统由微管组成（例如毛细血管、肺泡）。循环系统中的微管尽管千差万别，但总的来说，都具有层级结构，有自相似性。因为通过一个微管的体液流量正比于微管体积，所以微管总数{{Mvar|N}}正比于体液总流量，即 | ||
| 第9行： | 第9行： | ||
<blockquote><math>N^4\propto V^3</math></blockquote> | <blockquote><math>N^4\propto V^3</math></blockquote> | ||
再结合假设1、2，可得 | 再结合假设1、2，可得 | ||
| − | <blockquote><math>B\propto M^{\frac{3}{4}}</math> | + | <blockquote><math>B\propto M^{\frac{3}{4}}</math></blockquote> |
2021年8月14日 (六) 18:47的版本
克莱伯定律（Kleiber's law）[1]根据观测数据提出，对于很多动物，其基础代谢率水平与体重的¾次幂成正比，该定律得名于1930年代早期马克斯·克莱伯(Max Kleiber)的生物学著作。若用符号表示，设q0为该动物的代谢率，M是其重量，则q0 ~ M¾。因此一般一只猫的重量是一只老鼠的100倍，那么它的代谢量比老鼠约大31倍。而在植物中，指数则接近于1。
Figure 1. Body size versus metabolic rate for a variety of species[2]. Originally published in Kleiber (1947).
定律背后的原因
根据一些学者的研究[3][4]，克莱伯定律像许多其他的异速生长律定律一样，是动物循环系统物理学和几何学特性的结果。同一物种中，年轻的个体比年老的个体每份重量的呼吸消耗更多，因为它们体重中中组织结构的比例更大，而储能的比例较小。结构质量需要耗费养护能量，而储能的质量则不需要。
具体来说，West， Enquist和Brown提出三点假设（1）代谢率B正比于循环系统中的营养流量（即体液总流量）Q，即[math]\displaystyle{ B\propto Q }[/math]（2）体液（例如血液）总体积V正比于体重M，即[math]\displaystyle{ V \propto M }[/math]。这个假设的成立意味着循环系统中的能量耗散降至最低（3）循环系统由微管组成（例如毛细血管、肺泡）。循环系统中的微管尽管千差万别，但总的来说，都具有层级结构，有自相似性。因为通过一个微管的体液流量正比于微管体积，所以微管总数N正比于体液总流量，即
[math]\displaystyle{ Q\propto N }[/math]
另一方面，体液具有不可压缩性。而循环系统具有自相似性（假设3）。如果我们将循环系统描述为由大大小小的圆柱连接成的系统，那么以上两点就要求圆柱总数（即微管总数）{{Mvar|N}和体液总体积V满足
[math]\displaystyle{ N^4\propto V^3 }[/math]
再结合假设1、2，可得
[math]\displaystyle{ B\propto M^{\frac{3}{4}} }[/math]
参考资料
- ↑ Max Kleiber (1932). "Body size and metabolism". Hilgardia. 6: 315–351.
- ↑ Kleiber M (1947). "Body size and metabolic rate". Physiological Reviews. 27 (4): 511–541. PMID 20267758.
- ↑ West, Geoffreyt (1997). "A General Model for the Origin of Allometric Scaling Laws in Biology". Science. 276 (122).
- ↑ Shour, Robert (November 2012). "Entropy and its relationship to allometry". arXiv. arXiv:0804.1924.