“爱多士数”的版本间的差异
| 第6行: | 第6行: | ||
{{Short description|Closeness of someone's association with mathematician Paul Erdős}} | {{Short description|Closeness of someone's association with mathematician Paul Erdős}} | ||
| − | [[文件: | + | [[文件:保罗·埃尔德什Paul Erdős摄于1992年.jpg|缩略图|右]] |
| + | '''埃尔德什数 Erdős number'''(匈牙利语:[ˈɛrdøːʃ])根据数学论文的著作权来来对数学家保罗·埃尔德什与其他作者之间的“协作距离”进行描述。同样的原则也应用于很多当特定某个人与众多同行之间保持合作关系的其他领域。 | ||
| − | + | ==概况== | |
| − | |||
| − | |||
| − | == 概况== | ||
| − | |||
保罗·埃尔德什 Paul Erdős(1913年至1996年)是一位在业界产生有影响力的匈牙利数学家,其一生中大量的时间都在与很多同事合作撰写论文,致力于解决困扰已久的疑难数学问题。<ref name="newman2001">{{cite journal|last=Newman|first=Mark E. J.|title=The structure of scientific collaboration networks|journal=Proceedings of the National Academy of Sciences of the United States of America| year=2001| doi=10.1073/pnas.021544898| volume=98|issue=2|pages=404–409|pmid=11149952|pmc=14598}}</ref> 他一生中所发表的论文(至少1,525篇<ref>{{cite web |url=http://www.oakland.edu/enp/pubinfo/ |title=Publications of Paul Erdős | first=Jerry | last=Grossman |access-date=1 Feb 2011}}</ref>)比历史上其他任何数学家都多<ref name="newman2001"/>。莱昂哈德·欧拉 Leonhard Euler发表过的数学论文页数更多,但单独的论文却较少(大约800篇)。<ref>{{cite web| url=https://www.math.dartmouth.edu/~euler/FAQ.html| work=The Euler Archive| title=Frequently Asked Questions| publisher=Dartmouth College}}</ref>而埃尔德什的大部分时间都在旅居中,其拜访过全球500多个合作者。 | 保罗·埃尔德什 Paul Erdős(1913年至1996年)是一位在业界产生有影响力的匈牙利数学家,其一生中大量的时间都在与很多同事合作撰写论文,致力于解决困扰已久的疑难数学问题。<ref name="newman2001">{{cite journal|last=Newman|first=Mark E. J.|title=The structure of scientific collaboration networks|journal=Proceedings of the National Academy of Sciences of the United States of America| year=2001| doi=10.1073/pnas.021544898| volume=98|issue=2|pages=404–409|pmid=11149952|pmc=14598}}</ref> 他一生中所发表的论文(至少1,525篇<ref>{{cite web |url=http://www.oakland.edu/enp/pubinfo/ |title=Publications of Paul Erdős | first=Jerry | last=Grossman |access-date=1 Feb 2011}}</ref>)比历史上其他任何数学家都多<ref name="newman2001"/>。莱昂哈德·欧拉 Leonhard Euler发表过的数学论文页数更多,但单独的论文却较少(大约800篇)。<ref>{{cite web| url=https://www.math.dartmouth.edu/~euler/FAQ.html| work=The Euler Archive| title=Frequently Asked Questions| publisher=Dartmouth College}}</ref>而埃尔德什的大部分时间都在旅居中,其拜访过全球500多个合作者。 | ||
| − | |||
埃尔德什数的概念最初是由埃尔德什的朋友们提出来的,以赞扬保罗·埃尔德什的巨大成就。后来,它演变为研究数学家如何通过合作来解决问题的的工具而受到重视。有几个项目致力于使用埃尔德什数为代表方法来研究人员之间的连通性。<ref name="Erdős Number Project">{{cite web|url=http://www.oakland.edu/enp|title=Erdös Number Project|publisher=Oakland University}}</ref>例如,埃尔德什合作图可以告诉我们作者是如何聚集在一起的,每篇论文的共同作者数量随时间变化或新理论的产生如何传播的。<ref>{{cite web|url=http://www.oakland.edu/enp/trivia/|title=Facts about Erdös Numbers and the Collaboration Graph|work=Erdös Number Project|publisher=Oakland University}}</ref> | 埃尔德什数的概念最初是由埃尔德什的朋友们提出来的,以赞扬保罗·埃尔德什的巨大成就。后来,它演变为研究数学家如何通过合作来解决问题的的工具而受到重视。有几个项目致力于使用埃尔德什数为代表方法来研究人员之间的连通性。<ref name="Erdős Number Project">{{cite web|url=http://www.oakland.edu/enp|title=Erdös Number Project|publisher=Oakland University}}</ref>例如,埃尔德什合作图可以告诉我们作者是如何聚集在一起的,每篇论文的共同作者数量随时间变化或新理论的产生如何传播的。<ref>{{cite web|url=http://www.oakland.edu/enp/trivia/|title=Facts about Erdös Numbers and the Collaboration Graph|work=Erdös Number Project|publisher=Oakland University}}</ref> | ||
| − | |||
多项研究表明,领先的数学家往往具有极低的埃尔德什数。<ref name="trails">{{cite journal | 多项研究表明,领先的数学家往往具有极低的埃尔德什数。<ref name="trails">{{cite journal | ||
| 第38行: | 第33行: | ||
}} Original Spanish version in ''Rev. Acad. Colombiana Cienc. Exact. Fís. Natur.'' '''23''' (89) 563–582, 1999.</ref>菲尔兹奖得主Fields Medalists的埃尔德什中位数是3。只有7,097名(拥有合作经历的数学家中约5%)的埃尔德什数为2或更低。随着时间的流逝,低埃尔德什数的数学家因死亡而无法进行协作,所能达到的最小埃尔德什数必然会增加。历史人物仍可能一直具有较低的埃尔德什数。例如,印度著名数学家Srinivasa Ramanujan的埃尔德什数仅为3(通过与G. H. Hardy合作,其埃尔德什数为2),尽管Ramanujan去世时保罗·埃尔德什只有7岁。<ref name="paths"/> <ref name=":0" /> | }} Original Spanish version in ''Rev. Acad. Colombiana Cienc. Exact. Fís. Natur.'' '''23''' (89) 563–582, 1999.</ref>菲尔兹奖得主Fields Medalists的埃尔德什中位数是3。只有7,097名(拥有合作经历的数学家中约5%)的埃尔德什数为2或更低。随着时间的流逝,低埃尔德什数的数学家因死亡而无法进行协作,所能达到的最小埃尔德什数必然会增加。历史人物仍可能一直具有较低的埃尔德什数。例如,印度著名数学家Srinivasa Ramanujan的埃尔德什数仅为3(通过与G. H. Hardy合作,其埃尔德什数为2),尽管Ramanujan去世时保罗·埃尔德什只有7岁。<ref name="paths"/> <ref name=":0" /> | ||
| − | == 数学的定义与应用 == | + | ==数学的定义与应用== |
| − | |||
[[文件:Erdosnumber.png|缩略图|右|如果爱丽丝在一篇论文中与保罗·埃尔德什合作,在另一篇论文中与鲍勃合作,但是鲍勃从未与埃尔德什本人合作,那么爱丽丝的埃尔德什数为1,而鲍勃的埃尔德什数为2,因为他离埃尔德什有两步。]] | [[文件:Erdosnumber.png|缩略图|右|如果爱丽丝在一篇论文中与保罗·埃尔德什合作,在另一篇论文中与鲍勃合作,但是鲍勃从未与埃尔德什本人合作,那么爱丽丝的埃尔德什数为1,而鲍勃的埃尔德什数为2,因为他离埃尔德什有两步。]] | ||
| − | |||
要分配一个埃尔德什数,某人必须与另一个具有有限埃尔德什数的人共同撰写研究论文。保罗·埃尔德什的埃尔德什数为零。其他人的埃尔德什数为''k+1'',其中''k''是任何合著者中最低的埃尔德什数。美国数学学会提供免费的在线工具来确定《数学评论》目录中列出的每个数学作者的埃尔德什数。<ref name=":0">{{cite web|url=https://www.ams.org/mathscinet/collaborationDistance.html|title= Collaboration Distance|work=MathSciNet|publisher=American Mathematical Society}}</ref> | 要分配一个埃尔德什数,某人必须与另一个具有有限埃尔德什数的人共同撰写研究论文。保罗·埃尔德什的埃尔德什数为零。其他人的埃尔德什数为''k+1'',其中''k''是任何合著者中最低的埃尔德什数。美国数学学会提供免费的在线工具来确定《数学评论》目录中列出的每个数学作者的埃尔德什数。<ref name=":0">{{cite web|url=https://www.ams.org/mathscinet/collaborationDistance.html|title= Collaboration Distance|work=MathSciNet|publisher=American Mathematical Society}}</ref> | ||
| − | |||
埃尔德什一生撰写了约1500篇数学文章,其中大部分是合作的。他有511个直接合作者<ref name="Erdős Number Project"/>;这些是埃尔德什数为1的人。与这些人合作(但未与埃尔德什本人合作)的人所拥有的埃尔德什数为2(截至2020年8月7日为12,600人<ref name="Erdős Number Project File Erdos2">[https://www.oakland.edu/enp/thedata/erdos2/ Erdos2], Version 2020, 7 August 2020.</ref>),而与埃尔德什数为2的人合作的人(但与埃尔德什或埃尔德什数为1的任何人无合作关系),其埃尔德什数为3,依此类推。没有此类共同作者链接能指向埃尔德什的人,其埃尔德什数为无穷大(或未定义)。自保罗·埃尔德什逝世以来,新研究员可获得的最低埃尔德什数为2。 | 埃尔德什一生撰写了约1500篇数学文章,其中大部分是合作的。他有511个直接合作者<ref name="Erdős Number Project"/>;这些是埃尔德什数为1的人。与这些人合作(但未与埃尔德什本人合作)的人所拥有的埃尔德什数为2(截至2020年8月7日为12,600人<ref name="Erdős Number Project File Erdos2">[https://www.oakland.edu/enp/thedata/erdos2/ Erdos2], Version 2020, 7 August 2020.</ref>),而与埃尔德什数为2的人合作的人(但与埃尔德什或埃尔德什数为1的任何人无合作关系),其埃尔德什数为3,依此类推。没有此类共同作者链接能指向埃尔德什的人,其埃尔德什数为无穷大(或未定义)。自保罗·埃尔德什逝世以来,新研究员可获得的最低埃尔德什数为2。 | ||
| − | |||
关于具体由什么构成两位作者之间的联系,众说纷纭。美国数学学会的“协作距离计算器”使用的是来自《数学评论》的数据,包括大多数数学期刊,但仅以有限的方式涵盖了其他主题,同时还包括一些非研究出版物。埃尔德什数项目官方网站Erdős Number Project表示: | 关于具体由什么构成两位作者之间的联系,众说纷纭。美国数学学会的“协作距离计算器”使用的是来自《数学评论》的数据,包括大多数数学期刊,但仅以有限的方式涵盖了其他主题,同时还包括一些非研究出版物。埃尔德什数项目官方网站Erdős Number Project表示: | ||
...我们在顶点u和v之间共有的包含边标准是,它们之间的某些研究合作导致了发表的作品。任何数量的其他共同作者都是被允许的,... | ...我们在顶点u和v之间共有的包含边标准是,它们之间的某些研究合作导致了发表的作品。任何数量的其他共同作者都是被允许的,... | ||
| − | |||
但它们不包括非研究性出版物,例如教科书,联合编辑,讣告等。“第二种埃尔德什数”将其分配给只有两个合作者的论文。<ref>Grossman ''et al.'' "[http://www.oakland.edu/?id=9569&sid=243#en2k Erdős numbers of the second kind]," in ''Facts about Erdős Numbers and the Collaboration Graph''. [http://www.oakland.edu/enp The Erdős Number Project], Oakland University, USA. Retrieved July 25, 2009.</ref> | 但它们不包括非研究性出版物,例如教科书,联合编辑,讣告等。“第二种埃尔德什数”将其分配给只有两个合作者的论文。<ref>Grossman ''et al.'' "[http://www.oakland.edu/?id=9569&sid=243#en2k Erdős numbers of the second kind]," in ''Facts about Erdős Numbers and the Collaboration Graph''. [http://www.oakland.edu/enp The Erdős Number Project], Oakland University, USA. Retrieved July 25, 2009.</ref> | ||
| − | |||
埃尔德什数很可能最早由卡斯珀·高夫曼 Casper Goffman定义,他自己的埃尔德什数为2。<ref name="Erdős Number Project File Erdos2"/>高夫曼在1969年发表的一篇文章“您的埃尔德什数是多少”中表示了他对埃尔德什多产合作的看法<ref>{{cite journal|last=Goffman|first=Casper|title=And what is your Erdős number?|journal=American Mathematical Monthly|volume=76|year=1969|doi=10.2307/2317868|page=791|issue=7}}</ref>,另请参阅迈克尔·哥伦布 Michael Golomb在讣告中的一些评论。<ref>{{Cite web|url=https://www.math.purdue.edu/about/purview/fall96/paul-erdos.html|title=Paul Erdös at Purdue|website=www.math.purdue.edu}}</ref> | 埃尔德什数很可能最早由卡斯珀·高夫曼 Casper Goffman定义,他自己的埃尔德什数为2。<ref name="Erdős Number Project File Erdos2"/>高夫曼在1969年发表的一篇文章“您的埃尔德什数是多少”中表示了他对埃尔德什多产合作的看法<ref>{{cite journal|last=Goffman|first=Casper|title=And what is your Erdős number?|journal=American Mathematical Monthly|volume=76|year=1969|doi=10.2307/2317868|page=791|issue=7}}</ref>,另请参阅迈克尔·哥伦布 Michael Golomb在讣告中的一些评论。<ref>{{Cite web|url=https://www.math.purdue.edu/about/purview/fall96/paul-erdos.html|title=Paul Erdös at Purdue|website=www.math.purdue.edu}}</ref> | ||
| − | |||
菲尔兹奖获得者的埃尔德什中位数低至3。<ref name="paths"/>埃尔德什排名第二的奖牌获得者包括Atle Selberg,Kunihiko Kodaira,Klaus Roth,Alan Baker,Enrico Bombieri,David Mumford,Charles Fefferman,William Thurston,Shing-Tung Tung,Jean Bourgain,Richard Borcherds,Manjul Bhargava,Jean-Pierre Serre和陶哲轩。菲尔兹奖获得者中没有人的埃尔德什数为1。<ref name="project">{{cite web|url=http://www.oakland.edu/enp/erdpaths/|title=Paths to Erdös|work=The Erdös Number Project|publisher=Oakland University}}</ref>但是,恩德雷·塞梅雷迪 Endre Szemerédi是阿贝尔奖获得者,其埃尔德什数为1。<ref name="trails"/> | 菲尔兹奖获得者的埃尔德什中位数低至3。<ref name="paths"/>埃尔德什排名第二的奖牌获得者包括Atle Selberg,Kunihiko Kodaira,Klaus Roth,Alan Baker,Enrico Bombieri,David Mumford,Charles Fefferman,William Thurston,Shing-Tung Tung,Jean Bourgain,Richard Borcherds,Manjul Bhargava,Jean-Pierre Serre和陶哲轩。菲尔兹奖获得者中没有人的埃尔德什数为1。<ref name="project">{{cite web|url=http://www.oakland.edu/enp/erdpaths/|title=Paths to Erdös|work=The Erdös Number Project|publisher=Oakland University}}</ref>但是,恩德雷·塞梅雷迪 Endre Szemerédi是阿贝尔奖获得者,其埃尔德什数为1。<ref name="trails"/> | ||
| − | + | ==最频繁的埃尔德什合作者== | |
| − | == 最频繁的埃尔德什合作者 == | ||
| − | |||
虽然埃尔德什与数百位合著者合作,但其中一些人与他合作过数十篇论文。以下是最经常与埃尔德什合作的十人列表,以及与埃尔德什合作的论文数量(即合作数量)。<ref>Grossman, Jerry, [https://files.oakland.edu/users/grossman/enp/Erdos0p.html Erdos0p], Version 2010, ''[http://www.oakland.edu/enp The Erdős Number Project]'', Oakland University, US, October 20, 2010.</ref> | 虽然埃尔德什与数百位合著者合作,但其中一些人与他合作过数十篇论文。以下是最经常与埃尔德什合作的十人列表,以及与埃尔德什合作的论文数量(即合作数量)。<ref>Grossman, Jerry, [https://files.oakland.edu/users/grossman/enp/Erdos0p.html Erdos0p], Version 2010, ''[http://www.oakland.edu/enp The Erdős Number Project]'', Oakland University, US, October 20, 2010.</ref> | ||
| 第92行: | 第78行: | ||
|} | |} | ||
| − | + | ==相关领域== | |
| − | == | ||
截至2016年,所有菲尔兹奖章获得者都有一个有限的埃尔德什数,其值在2到6之间,中位数为3。相反,所有数学家的埃尔德什数的中位数(有限的埃尔德什数)为5,极限值为13。<ref>{{Cite web|url=http://wwwp.oakland.edu/enp/trivia/|title=Facts about Erdös Numbers and the Collaboration Graph - The Erdös Number Project- Oakland University|website=wwwp.oakland.edu|access-date=2016-10-27}}</ref>下表总结了物理,化学,医学和经济学方面的诺贝尔奖得主的埃尔德什数统计。<ref>{{Cite journal|last=López de Prado|first=Marcos|title=Mathematics and Economics: A reality check|journal=The Journal of Portfolio Management|volume=43|issue=1|pages=5–8|doi=10.3905/jpm.2016.43.1.005|year=2016}}</ref>第一列计算获奖人数。第二列计算的是具有有限埃尔德什数的获胜者数量。第三列是具有有限埃尔德什数的获胜者的百分比。其余各列表示了这些获奖者中埃尔德什数的最小,最大,平均和中位数。 | 截至2016年,所有菲尔兹奖章获得者都有一个有限的埃尔德什数,其值在2到6之间,中位数为3。相反,所有数学家的埃尔德什数的中位数(有限的埃尔德什数)为5,极限值为13。<ref>{{Cite web|url=http://wwwp.oakland.edu/enp/trivia/|title=Facts about Erdös Numbers and the Collaboration Graph - The Erdös Number Project- Oakland University|website=wwwp.oakland.edu|access-date=2016-10-27}}</ref>下表总结了物理,化学,医学和经济学方面的诺贝尔奖得主的埃尔德什数统计。<ref>{{Cite journal|last=López de Prado|first=Marcos|title=Mathematics and Economics: A reality check|journal=The Journal of Portfolio Management|volume=43|issue=1|pages=5–8|doi=10.3905/jpm.2016.43.1.005|year=2016}}</ref>第一列计算获奖人数。第二列计算的是具有有限埃尔德什数的获胜者数量。第三列是具有有限埃尔德什数的获胜者的百分比。其余各列表示了这些获奖者中埃尔德什数的最小,最大,平均和中位数。 | ||
| 第153行: | 第138行: | ||
|} | |} | ||
| − | + | ===物理领域=== | |
| − | === 物理领域 === | ||
在诺贝尔物理学奖获得者中,爱因斯坦 Albert Einstein和谢尔登·李·格拉肖 Sheldon Lee Glashow的埃尔德什数为2。诺贝尔奖获得者中埃尔德什数为3的有: Enrico Fermi,Otto Stern,Wolfgang Pauli,Max Born,Willis E.Lamb,Eugene Wigner,Richard P.Feynman,Hans A.Bethe,Murray Gell-Mann,Abdus Salam,Steven Weinberg,Norman F.Ramsey,Frank Wilczek和David Wineland。获得菲尔兹奖的物理学家Ed Witten的埃尔德什数为3。<ref name="paths">{{Cite web |title = Some Famous People with Finite Erdős Numbers |url = http://www.oakland.edu/enp/erdpaths/ |publisher =oakland.edu |access-date = 4 April 2014 }}</ref> | 在诺贝尔物理学奖获得者中,爱因斯坦 Albert Einstein和谢尔登·李·格拉肖 Sheldon Lee Glashow的埃尔德什数为2。诺贝尔奖获得者中埃尔德什数为3的有: Enrico Fermi,Otto Stern,Wolfgang Pauli,Max Born,Willis E.Lamb,Eugene Wigner,Richard P.Feynman,Hans A.Bethe,Murray Gell-Mann,Abdus Salam,Steven Weinberg,Norman F.Ramsey,Frank Wilczek和David Wineland。获得菲尔兹奖的物理学家Ed Witten的埃尔德什数为3。<ref name="paths">{{Cite web |title = Some Famous People with Finite Erdős Numbers |url = http://www.oakland.edu/enp/erdpaths/ |publisher =oakland.edu |access-date = 4 April 2014 }}</ref> | ||
| − | + | ===生物学领域=== | |
| − | === 生物学领域 === | ||
计算生物学家Lior Pachter的埃尔德什数为2。<ref name="erdos2">{{cite web |title=List of all people with Erdos number less than or equal to 2 |url=https://files.oakland.edu/users/grossman/enp/ErdosA.html |work=The Erdös Number Project |publisher=Oakland University |date=14 July 2015 |access-date=25 August 2015}}</ref>进化生物学家Richard Lenski的埃尔德什数为3,与Lior Pachter和数学家Bernd Sturmfels共同撰写了出版物的每位作者埃尔德什数为2。<ref>{{cite web|url=http://telliamedrevisited.wordpress.com/2015/05/28/erdos-with-a-non-kosher-side-of-bacon|title=Erdös with a non-kosher side of Bacon|author=Richard Lenski|date=May 28, 2015}}</ref> | 计算生物学家Lior Pachter的埃尔德什数为2。<ref name="erdos2">{{cite web |title=List of all people with Erdos number less than or equal to 2 |url=https://files.oakland.edu/users/grossman/enp/ErdosA.html |work=The Erdös Number Project |publisher=Oakland University |date=14 July 2015 |access-date=25 August 2015}}</ref>进化生物学家Richard Lenski的埃尔德什数为3,与Lior Pachter和数学家Bernd Sturmfels共同撰写了出版物的每位作者埃尔德什数为2。<ref>{{cite web|url=http://telliamedrevisited.wordpress.com/2015/05/28/erdos-with-a-non-kosher-side-of-bacon|title=Erdös with a non-kosher side of Bacon|author=Richard Lenski|date=May 28, 2015}}</ref> | ||
| − | + | ===财经领域=== | |
| − | ===财经领域 === | ||
至少有两名诺贝尔经济学奖获得者的埃尔德什数为2:哈里·马可维兹 Harry M. Markowitz,(1990)和列昂尼德·坎托罗维奇 Leonid Kantorovich(1975)。埃尔德什数为2的其他金融数学家包括David Donoho,Marc Yor,Henry McKean,Daniel Stroock和Joseph Keller。 | 至少有两名诺贝尔经济学奖获得者的埃尔德什数为2:哈里·马可维兹 Harry M. Markowitz,(1990)和列昂尼德·坎托罗维奇 Leonid Kantorovich(1975)。埃尔德什数为2的其他金融数学家包括David Donoho,Marc Yor,Henry McKean,Daniel Stroock和Joseph Keller。 | ||
| − | |||
埃尔德什数为3的诺贝尔经济学奖得主,其中包括Kenneth J. Arrow(1972),Milton Friedman(1976),Herbert A. Simon(1978),Gerard Debreu(1983),John Forbes Nash,Jr.(1994),James Mirrlees(1996),Daniel McFadden(2000),Daniel Kahneman(2002),Robert J.Aumann(2005),Leonid Hurwicz(2007),Roger Myerson(2007),Alvin E.Roth(2012)和Lloyd S. Shapley(2012)和Jean Tirole(2014)。<ref>Grossman, J. (2015): "The Erdős Number Project." http://wwwp.oakland.edu/enp/erdpaths/</ref> | 埃尔德什数为3的诺贝尔经济学奖得主,其中包括Kenneth J. Arrow(1972),Milton Friedman(1976),Herbert A. Simon(1978),Gerard Debreu(1983),John Forbes Nash,Jr.(1994),James Mirrlees(1996),Daniel McFadden(2000),Daniel Kahneman(2002),Robert J.Aumann(2005),Leonid Hurwicz(2007),Roger Myerson(2007),Alvin E.Roth(2012)和Lloyd S. Shapley(2012)和Jean Tirole(2014)。<ref>Grossman, J. (2015): "The Erdős Number Project." http://wwwp.oakland.edu/enp/erdpaths/</ref> | ||
| − | |||
一些埃尔德什数低的数学家创立了投资公司,其中包括Axcom Technologies的James B. Ax和Renaissance Technologies的James H. Simons,两者的埃尔德什数均为3。<ref>{{Cite news|url=https://www.bloomberg.com/news/articles/2016-11-11/six-degrees-of-quant-kevin-bacon-and-the-erdos-number-mystery|title=Six Degrees of Quant: Kevin Bacon and the Erdős Number Mystery|last=Kishan|first=Saijel|date=2016-11-11|newspaper=Bloomberg.com|access-date=2016-11-12}}</ref><ref>{{Cite news|url=http://www.financial-math.org/blog/2016/11/erdos-numbers-in-finance/|title=Erdős Numbers: A True "Prince and the Pauper" story|last=Bailey|first=David H.|date=2016-11-06|newspaper=The Mathematical Investor|language=en-US|access-date=2016-11-12}}</ref> | 一些埃尔德什数低的数学家创立了投资公司,其中包括Axcom Technologies的James B. Ax和Renaissance Technologies的James H. Simons,两者的埃尔德什数均为3。<ref>{{Cite news|url=https://www.bloomberg.com/news/articles/2016-11-11/six-degrees-of-quant-kevin-bacon-and-the-erdos-number-mystery|title=Six Degrees of Quant: Kevin Bacon and the Erdős Number Mystery|last=Kishan|first=Saijel|date=2016-11-11|newspaper=Bloomberg.com|access-date=2016-11-12}}</ref><ref>{{Cite news|url=http://www.financial-math.org/blog/2016/11/erdos-numbers-in-finance/|title=Erdős Numbers: A True "Prince and the Pauper" story|last=Bailey|first=David H.|date=2016-11-06|newspaper=The Mathematical Investor|language=en-US|access-date=2016-11-12}}</ref> | ||
| − | + | ===哲学领域=== | |
| − | === 哲学领域 === | ||
由于哲学的本质与数学基础缘由互通,因此它们有很多重叠的地方,许多哲学家都可以使用埃尔德什数。<ref>{{cite web |url=http://home.iprimus.com.au/than/toby/2013-researchnetwork-poster.pdf |title=Philosophy research networks |author=Toby Handfield |archive-url=https://web.archive.org/web/20160221161316/http://home.iprimus.com.au/than/toby/2013-researchnetwork-poster.pdf |archive-date=2016-02-21 }}</ref>哲学家John P. Burgess的埃尔德什数为2。<ref name="erdos2"/>Barwise和Joel David Hamkins埃尔德什数都为2,他们为哲学做出了大量贡献,但通常被称为数学家。 | 由于哲学的本质与数学基础缘由互通,因此它们有很多重叠的地方,许多哲学家都可以使用埃尔德什数。<ref>{{cite web |url=http://home.iprimus.com.au/than/toby/2013-researchnetwork-poster.pdf |title=Philosophy research networks |author=Toby Handfield |archive-url=https://web.archive.org/web/20160221161316/http://home.iprimus.com.au/than/toby/2013-researchnetwork-poster.pdf |archive-date=2016-02-21 }}</ref>哲学家John P. Burgess的埃尔德什数为2。<ref name="erdos2"/>Barwise和Joel David Hamkins埃尔德什数都为2,他们为哲学做出了大量贡献,但通常被称为数学家。 | ||
| − | + | ===法律领域=== | |
| − | === 法律领域 === | ||
与Alvin E. Roth合作的法官Richard Posner的埃尔德什数最多为4。在哈佛法学院任教的政治家,哲学家和法律理论家Roberto Mangabeira Unger与Lee Smolin曾经合作过,其埃尔德什数最多为4。 | 与Alvin E. Roth合作的法官Richard Posner的埃尔德什数最多为4。在哈佛法学院任教的政治家,哲学家和法律理论家Roberto Mangabeira Unger与Lee Smolin曾经合作过,其埃尔德什数最多为4。 | ||
| − | + | ===政治领域=== | |
| − | === 政治领域 === | ||
从2005年至今的德国总理安格拉·默克尔 Angela Merkel的埃尔德什数最多为5。<ref name="project"/> | 从2005年至今的德国总理安格拉·默克尔 Angela Merkel的埃尔德什数最多为5。<ref name="project"/> | ||
| − | + | ===工程领域=== | |
| − | === 工程领域 === | ||
工程的某些领域,尤其是通信理论和密码学,直接利用了埃尔德什数主要涉及的离散数学。因此,这些领域的从业人员的埃尔德什数低就不足为奇了。例如,加州理工学院电气工程学教授Robert McEliece与埃尔德什本人合作,其埃尔德什数为1。<ref>{{cite journal |author=Erdős, Paul, Robert McEliece, and Herbert Taylor |title=Ramsey bounds for graph products |journal=Pacific Journal of Mathematics|volume=37 |issue=1 |date=1971 |pages=45–46 |url=https://msp.org/pjm/1971/37-1/pjm-v37-n1-p07-p.pdf |doi=10.2140/pjm.1971.37.45|doi-access=free }}</ref>RSA密码系统的发明者,密码学家Ron Rivest,Adi Shamir和Leonard Adleman的埃尔德什数均为2。<ref name="erdos2"/> | 工程的某些领域,尤其是通信理论和密码学,直接利用了埃尔德什数主要涉及的离散数学。因此,这些领域的从业人员的埃尔德什数低就不足为奇了。例如,加州理工学院电气工程学教授Robert McEliece与埃尔德什本人合作,其埃尔德什数为1。<ref>{{cite journal |author=Erdős, Paul, Robert McEliece, and Herbert Taylor |title=Ramsey bounds for graph products |journal=Pacific Journal of Mathematics|volume=37 |issue=1 |date=1971 |pages=45–46 |url=https://msp.org/pjm/1971/37-1/pjm-v37-n1-p07-p.pdf |doi=10.2140/pjm.1971.37.45|doi-access=free }}</ref>RSA密码系统的发明者,密码学家Ron Rivest,Adi Shamir和Leonard Adleman的埃尔德什数均为2。<ref name="erdos2"/> | ||
| − | + | ===社交网络分析领域=== | |
| − | === 社交网络分析领域 === | ||
人类学家道格拉斯·怀特 Douglas R. White通过与图论家弗兰克·哈拉里 Frank Harary合作得到埃尔德什数为2。<ref>{{cite journal | last1 = White | first1 = Douglas R. | last2 = Harary | first2 = Frank | year = 2001 | title = The Cohesiveness of Blocks in Social Networks: Node Connectivity and Conditional Density | url = https://escholarship.org/uc/item/8585j6z4| journal = Sociological Methodology | volume = 31 | pages = 305–59 | doi = 10.1111/0081-1750.00098 }}</ref><ref>{{cite web |url=http://eclectic.ss.uci.edu/~drwhite/6wwwvita.html |title=VITA: Douglas R.White, Anthropology & Social Science Professor, UC-Irvine |access-date=December 14, 2017}}</ref>社会学家巴里·韦尔曼 Barry Wellman通过与社交网络分析师和统计学家 Ove Frank<ref>Barry Wellman, Ove Frank, Vicente Espinoza, Staffan Lundquist and Craig Wilson. "Integrating Individual, Relational and Structural Analysis". 1991. ''Social Networks'' 13 (Sept.): 223-50.</ref>(Harve's的另一位合作者)<ref>Ove Frank; Frank Harary, "Cluster Inference by Using Transitivity Indices in Empirical Graphs." ''Journal of the American Statistical Association'', 77, 380. (Dec., 1982), pp. 835–840.</ref>合作得到了埃尔德什数为3。 | 人类学家道格拉斯·怀特 Douglas R. White通过与图论家弗兰克·哈拉里 Frank Harary合作得到埃尔德什数为2。<ref>{{cite journal | last1 = White | first1 = Douglas R. | last2 = Harary | first2 = Frank | year = 2001 | title = The Cohesiveness of Blocks in Social Networks: Node Connectivity and Conditional Density | url = https://escholarship.org/uc/item/8585j6z4| journal = Sociological Methodology | volume = 31 | pages = 305–59 | doi = 10.1111/0081-1750.00098 }}</ref><ref>{{cite web |url=http://eclectic.ss.uci.edu/~drwhite/6wwwvita.html |title=VITA: Douglas R.White, Anthropology & Social Science Professor, UC-Irvine |access-date=December 14, 2017}}</ref>社会学家巴里·韦尔曼 Barry Wellman通过与社交网络分析师和统计学家 Ove Frank<ref>Barry Wellman, Ove Frank, Vicente Espinoza, Staffan Lundquist and Craig Wilson. "Integrating Individual, Relational and Structural Analysis". 1991. ''Social Networks'' 13 (Sept.): 223-50.</ref>(Harve's的另一位合作者)<ref>Ove Frank; Frank Harary, "Cluster Inference by Using Transitivity Indices in Empirical Graphs." ''Journal of the American Statistical Association'', 77, 380. (Dec., 1982), pp. 835–840.</ref>合作得到了埃尔德什数为3。 | ||
| − | + | ===语言学领域=== | |
| − | === 语言学领域 === | ||
罗马尼亚数学家和计算语言学家Solomon Marcus在1957年与埃尔德什合作了《 Acta Mathematica Hungarica》中的一篇论文,因此他的埃尔德什数为1。<ref>{{cite journal|first1=Paul|last1= Erdős |first2= Solomon|last2= Marcus| year=1957|title= Sur la décomposition de l'espace euclidien en ensembles homogènes |trans-title= On the decomposition of the Euclidean space into homogeneous sets|journal=Acta Mathematica Hungarica|volume=8|issue= 3–4 |pages=443–452|doi=10.1007/BF02020326 }}</ref> | 罗马尼亚数学家和计算语言学家Solomon Marcus在1957年与埃尔德什合作了《 Acta Mathematica Hungarica》中的一篇论文,因此他的埃尔德什数为1。<ref>{{cite journal|first1=Paul|last1= Erdős |first2= Solomon|last2= Marcus| year=1957|title= Sur la décomposition de l'espace euclidien en ensembles homogènes |trans-title= On the decomposition of the Euclidean space into homogeneous sets|journal=Acta Mathematica Hungarica|volume=8|issue= 3–4 |pages=443–452|doi=10.1007/BF02020326 }}</ref> | ||
| − | + | ==影响== | |
| − | ==影响 == | ||
| − | |||
[[文件:Paul Erdos with Terence Tao.jpg|缩略图|右|1985年,保罗·埃尔德什在阿德莱德大学任教,他的学生陶哲轩 Terence Tao当时只有10岁。陶后来成为加州大学洛杉矶分校的数学教授,于2006年获得菲尔兹奖,并于2007年当选为皇家学会会员。他的埃尔德什数为2。]] | [[文件:Paul Erdos with Terence Tao.jpg|缩略图|右|1985年,保罗·埃尔德什在阿德莱德大学任教,他的学生陶哲轩 Terence Tao当时只有10岁。陶后来成为加州大学洛杉矶分校的数学教授,于2006年获得菲尔兹奖,并于2007年当选为皇家学会会员。他的埃尔德什数为2。]] | ||
多年以来,埃尔德什数在数学家之间一直盛行。在千年之交的所有在职数学家中,都伴随着一个有限埃尔德什数,数字范围最大为15,中位数为5,平均值为4.65。<ref name="Erdős Number Project"/>几乎每个具有有限埃尔德什数的人其数字都小于8。由于当今科学领域跨学科合作的频率很高,因此许多其他科学领域的大量非数学家也具有有限的埃尔德什数。<ref>{{cite web |url=http://www.oakland.edu/enp/erdpaths/ |title=Some Famous People with Finite Erdős Numbers | first=Jerry | last=Grossman |access-date=1 February 2011}}</ref>例如,政治学家Steven Brams的埃尔德什数为2。在生物医学研究中,统计学家通常是出版物的作者,许多统计学家可以通过John Tukey(其埃尔德什数为2)与埃尔德什链接。同样,著名的遗传学家Eric Lander和数学家Daniel Kleitman在论文上进行了合作,<ref>{{cite journal | pmid = 10582576 | doi=10.1089/106652799318364 | volume=6 | title=A dictionary-based approach for gene annotation | year=1999 | journal=J Comput Biol | pages=419–30 | last1 = Pachter | first1 = L | last2 = Batzoglou | first2 = S | last3 = Spitkovsky | first3 = VI | last4 = Banks | first4 = E | last5 = Lander | first5 = ES | last6 = Kleitman | first6 = DJ | last7 = Berger | first7 = B| issue=3–4 }}</ref><ref>{{cite web|url=http://www-math.mit.edu/~djk/list.html|title=Publications Since 1980 more or less|first=Daniel|last=Kleitman|publisher=Massachusetts Institute of Technology}}</ref>由于Kleitman的埃尔德什数为1,<ref> | 多年以来,埃尔德什数在数学家之间一直盛行。在千年之交的所有在职数学家中,都伴随着一个有限埃尔德什数,数字范围最大为15,中位数为5,平均值为4.65。<ref name="Erdős Number Project"/>几乎每个具有有限埃尔德什数的人其数字都小于8。由于当今科学领域跨学科合作的频率很高,因此许多其他科学领域的大量非数学家也具有有限的埃尔德什数。<ref>{{cite web |url=http://www.oakland.edu/enp/erdpaths/ |title=Some Famous People with Finite Erdős Numbers | first=Jerry | last=Grossman |access-date=1 February 2011}}</ref>例如,政治学家Steven Brams的埃尔德什数为2。在生物医学研究中,统计学家通常是出版物的作者,许多统计学家可以通过John Tukey(其埃尔德什数为2)与埃尔德什链接。同样,著名的遗传学家Eric Lander和数学家Daniel Kleitman在论文上进行了合作,<ref>{{cite journal | pmid = 10582576 | doi=10.1089/106652799318364 | volume=6 | title=A dictionary-based approach for gene annotation | year=1999 | journal=J Comput Biol | pages=419–30 | last1 = Pachter | first1 = L | last2 = Batzoglou | first2 = S | last3 = Spitkovsky | first3 = VI | last4 = Banks | first4 = E | last5 = Lander | first5 = ES | last6 = Kleitman | first6 = DJ | last7 = Berger | first7 = B| issue=3–4 }}</ref><ref>{{cite web|url=http://www-math.mit.edu/~djk/list.html|title=Publications Since 1980 more or less|first=Daniel|last=Kleitman|publisher=Massachusetts Institute of Technology}}</ref>由于Kleitman的埃尔德什数为1,<ref> | ||
{{cite journal | last1 = Erdős | first1 = Paul | author1-link = Paul Erdős |last2=Kleitman|first2=Daniel | title = On Collections of Subsets Containing No 4-Member Boolean Algebra | journal = Proceedings of the American Mathematical Society | volume = 28 | issue = 1 | pages = 87–90 |date=April 1971 | doi = 10.2307/2037762|url=http://www.math-inst.hu/~p_erdos/1971-07.pdf}}</ref>因此可以通过Lander及其众多合作者将遗传学和基因组学领域的大部分联系起来。另外,与Gustavus Simmons的合作为密码研究界内的埃尔德什数打开了大门,许多语言学家拥有有限的埃尔德什数,这许多是由于与Noam Chomsky(埃尔德什数为4),<ref>{{cite web |last=von Fintel |first=Kai |title=My Erdös Number is 8 |url=http://semantics-online.org/2004/01/my-erds-number-is-8 |publisher=Semantics, Inc. |date=2004 |archive-url=https://web.archive.org/web/20060823085712/http://semantics-online.org/2004/01/my-erds-number-is-8 |archive-date=23 August 2006}}</ref>William Labov(埃尔德什数为3)等著名学者的合作产生,<ref>{{cite web|url=http://www.ling.upenn.edu/~dinkin/ |title=Aaron Dinkin has a web site? |publisher=Ling.upenn.edu |access-date=2010-08-29}}</ref>类似有Mark Liberman(3)<ref>{{cite web|url=http://www.ling.upenn.edu/~myl/ |title=Mark Liberman's Home Page |publisher=Ling.upenn.edu |access-date=2010-08-29}}</ref> ,Geoffrey Pullum(3)<ref>{{cite web|url=http://www.stanford.edu/~cgpotts/miscellany.html |title=Christopher Potts: Miscellany |publisher=Stanford.edu |access-date=2010-08-29}}</ref>或Ivan Sag(4)<ref>{{cite web|url=http://lingo.stanford.edu/sag/erdos.html |title=Bob's Erdős Number |publisher=Lingo.stanford.edu |access-date=2010-08-29}}</ref>。同时与艺术领域也有联系。<ref>{{cite conference | last1=Bowen | first1=Jonathan P. | last2=Wilson | first2=Robin J. | editor1-first=Stuart|editor1-last=Dunn|editor2-first=Jonathan P.|editor2-last=Bowen|editor3-first= Kia|editor3-last=Ng | title=Visualising Virtual Communities: From Erdős to the Arts | url=http://ewic.bcs.org/content/ConWebDoc/46141 | book-title= EVA London 2012: Electronic Visualisation and the Arts | publisher=British Computer Society | series= Electronic Workshops in Computing | pages = 238–244 |date=10–12 July 2012}}</ref> | {{cite journal | last1 = Erdős | first1 = Paul | author1-link = Paul Erdős |last2=Kleitman|first2=Daniel | title = On Collections of Subsets Containing No 4-Member Boolean Algebra | journal = Proceedings of the American Mathematical Society | volume = 28 | issue = 1 | pages = 87–90 |date=April 1971 | doi = 10.2307/2037762|url=http://www.math-inst.hu/~p_erdos/1971-07.pdf}}</ref>因此可以通过Lander及其众多合作者将遗传学和基因组学领域的大部分联系起来。另外,与Gustavus Simmons的合作为密码研究界内的埃尔德什数打开了大门,许多语言学家拥有有限的埃尔德什数,这许多是由于与Noam Chomsky(埃尔德什数为4),<ref>{{cite web |last=von Fintel |first=Kai |title=My Erdös Number is 8 |url=http://semantics-online.org/2004/01/my-erds-number-is-8 |publisher=Semantics, Inc. |date=2004 |archive-url=https://web.archive.org/web/20060823085712/http://semantics-online.org/2004/01/my-erds-number-is-8 |archive-date=23 August 2006}}</ref>William Labov(埃尔德什数为3)等著名学者的合作产生,<ref>{{cite web|url=http://www.ling.upenn.edu/~dinkin/ |title=Aaron Dinkin has a web site? |publisher=Ling.upenn.edu |access-date=2010-08-29}}</ref>类似有Mark Liberman(3)<ref>{{cite web|url=http://www.ling.upenn.edu/~myl/ |title=Mark Liberman's Home Page |publisher=Ling.upenn.edu |access-date=2010-08-29}}</ref> ,Geoffrey Pullum(3)<ref>{{cite web|url=http://www.stanford.edu/~cgpotts/miscellany.html |title=Christopher Potts: Miscellany |publisher=Stanford.edu |access-date=2010-08-29}}</ref>或Ivan Sag(4)<ref>{{cite web|url=http://lingo.stanford.edu/sag/erdos.html |title=Bob's Erdős Number |publisher=Lingo.stanford.edu |access-date=2010-08-29}}</ref>。同时与艺术领域也有联系。<ref>{{cite conference | last1=Bowen | first1=Jonathan P. | last2=Wilson | first2=Robin J. | editor1-first=Stuart|editor1-last=Dunn|editor2-first=Jonathan P.|editor2-last=Bowen|editor3-first= Kia|editor3-last=Ng | title=Visualising Virtual Communities: From Erdős to the Arts | url=http://ewic.bcs.org/content/ConWebDoc/46141 | book-title= EVA London 2012: Electronic Visualisation and the Arts | publisher=British Computer Society | series= Electronic Workshops in Computing | pages = 238–244 |date=10–12 July 2012}}</ref> | ||
| − | |||
根据亚历克斯·洛佩兹·奥尔蒂斯 Alex Lopez-Ortiz的说法,在1986年至1994年的三个周期中,所有菲尔兹奖和内凡琳娜奖 Nevanlinna prize得主的埃尔德什数最多为9。 | 根据亚历克斯·洛佩兹·奥尔蒂斯 Alex Lopez-Ortiz的说法,在1986年至1994年的三个周期中,所有菲尔兹奖和内凡琳娜奖 Nevanlinna prize得主的埃尔德什数最多为9。 | ||
| − | |||
较早的数学家发表的论文通常少于现代的,而且很少发表联合论文。已知拥有有限埃尔德什数的最早学者是Antoine Lavoisier(生于1743年,埃尔德什数为13),Richard Dedekind(生于1831年,埃尔德什数为7)或Ferdinand Georg Frobenius(生于1849年,埃尔德什数为3),具体取决于出版物资格标准。<ref>{{cite web|url=http://www.oakland.edu/enp/erdpaths |title=Paths to Erdös - The Erdös Number Project- Oakland University|work=oakland.edu}}</ref> | 较早的数学家发表的论文通常少于现代的,而且很少发表联合论文。已知拥有有限埃尔德什数的最早学者是Antoine Lavoisier(生于1743年,埃尔德什数为13),Richard Dedekind(生于1831年,埃尔德什数为7)或Ferdinand Georg Frobenius(生于1849年,埃尔德什数为3),具体取决于出版物资格标准。<ref>{{cite web|url=http://www.oakland.edu/enp/erdpaths |title=Paths to Erdös - The Erdös Number Project- Oakland University|work=oakland.edu}}</ref> | ||
| − | |||
马丁·汤帕 Martin Tompa<ref>{{cite journal|last=Tompa|first=Martin|title=Figures of merit|journal=ACM SIGACT News|volume=20|issue=1|pages=62–71|year=1989|doi=10.1145/65780.65782}} {{cite journal|last=Tompa|first= Martin|title=Figures of merit: the sequel|journal=ACM SIGACT News|volume=21|issue=4|pages=78–81|year=1990|doi=10.1145/101371.101376}}</ref> 提出了埃尔德什数问题的有向图版本,通过定向协作图,将字母顺序更早的作者到字母顺序更晚的作者进行排列,并将作者的单调埃尔德什数定义为该有向图中从埃尔德什到作者的最长路径的长度。他发现这种路径长度为12。 | 马丁·汤帕 Martin Tompa<ref>{{cite journal|last=Tompa|first=Martin|title=Figures of merit|journal=ACM SIGACT News|volume=20|issue=1|pages=62–71|year=1989|doi=10.1145/65780.65782}} {{cite journal|last=Tompa|first= Martin|title=Figures of merit: the sequel|journal=ACM SIGACT News|volume=21|issue=4|pages=78–81|year=1990|doi=10.1145/101371.101376}}</ref> 提出了埃尔德什数问题的有向图版本,通过定向协作图,将字母顺序更早的作者到字母顺序更晚的作者进行排列,并将作者的单调埃尔德什数定义为该有向图中从埃尔德什到作者的最长路径的长度。他发现这种路径长度为12。 | ||
| − | |||
另外,迈克尔·巴尔 Michael Barr曾建议使用“合理的埃尔德什数”,通俗的说就是与埃尔德共同撰写过''p''篇论文的人应被分配埃尔德什数的''1/p''。根据第二种的协作多重图(尽管他也有办法处理第一种情况),即在他们所合著的每篇联合论文中,两个数学家之间都有一条边,我们可以将其视为这个网络视每一条边上都有一个1欧姆电阻器的电网。两个节点之间的总电阻表明这两个节点有多“相近”。 | 另外,迈克尔·巴尔 Michael Barr曾建议使用“合理的埃尔德什数”,通俗的说就是与埃尔德共同撰写过''p''篇论文的人应被分配埃尔德什数的''1/p''。根据第二种的协作多重图(尽管他也有办法处理第一种情况),即在他们所合著的每篇联合论文中,两个数学家之间都有一条边,我们可以将其视为这个网络视每一条边上都有一个1欧姆电阻器的电网。两个节点之间的总电阻表明这两个节点有多“相近”。 | ||
| − | |||
有人提出:“对于独立研究人员而言,诸如埃尔德什数之类的量度可以捕获网络的结构特性,而''h''指数则可以捕获出版物的引文影响。” 并且“可以很容易地使人相信,共同作者网络中的排名应该同时考虑到两种方法,以产生现实且可接受的排名。”<ref name=Dixit>Kashyap Dixit, S Kameshwaran, Sameep Mehta, Vinayaka Pandit, N Viswanadham, ''[http://domino.research.ibm.com/library/cyberdig.nsf/papers/2B600A90C54E51B18525755800283D37/$File/RR_ranking.pdf Towards simultaneously exploiting structure and outcomes in interaction networks for node ranking]'', IBM Research Report R109002, February 2009; also appeared as {{Cite journal | doi = 10.1145/1871437.1871470| last1 = Kameshwaran | first1 = S. | last2 = Pandit | first2 = V. | last3 = Mehta | first3 = S. | last4 = Viswanadham | first4 = N. | last5 = Dixit | first5 = K. | title = Outcome aware ranking in interaction networks | pages = 229–238| year = 2010 | journal = Proceedings of the 19th ACM International Conference on Information and Knowledge Management (CIKM '10)| url = http://www.cse.iitd.ernet.in/%7Epandit/cikm_camera_ready.pdf}}</ref> | 有人提出:“对于独立研究人员而言,诸如埃尔德什数之类的量度可以捕获网络的结构特性,而''h''指数则可以捕获出版物的引文影响。” 并且“可以很容易地使人相信,共同作者网络中的排名应该同时考虑到两种方法,以产生现实且可接受的排名。”<ref name=Dixit>Kashyap Dixit, S Kameshwaran, Sameep Mehta, Vinayaka Pandit, N Viswanadham, ''[http://domino.research.ibm.com/library/cyberdig.nsf/papers/2B600A90C54E51B18525755800283D37/$File/RR_ranking.pdf Towards simultaneously exploiting structure and outcomes in interaction networks for node ranking]'', IBM Research Report R109002, February 2009; also appeared as {{Cite journal | doi = 10.1145/1871437.1871470| last1 = Kameshwaran | first1 = S. | last2 = Pandit | first2 = V. | last3 = Mehta | first3 = S. | last4 = Viswanadham | first4 = N. | last5 = Dixit | first5 = K. | title = Outcome aware ranking in interaction networks | pages = 229–238| year = 2010 | journal = Proceedings of the 19th ACM International Conference on Information and Knowledge Management (CIKM '10)| url = http://www.cse.iitd.ernet.in/%7Epandit/cikm_camera_ready.pdf}}</ref> | ||
| − | |||
2004年,数学家埃尔德什数为4的William Tozier在eBay上拍卖了合著者,因此为买家提供了埃尔德什数为5的机会。一位西班牙数学家发布了1031美元的中标价格。不过他并不打算付款,而只是进行出价以阻止他认为是嘲弄的行为。<ref>Clifford A. Pickover: ''A Passion for Mathematics: Numbers, Puzzles, Madness, Religion, and the Quest for Reality''. Wiley, 2011, S. 33</ref><ref>{{cite journal | last1 = Klarreich | first1 = Erica | year = 2004 | title = Theorem for Sale | journal = Science News | volume = 165 | issue = 24| pages = 376–377 | doi = 10.2307/4015267 }}</ref> | 2004年,数学家埃尔德什数为4的William Tozier在eBay上拍卖了合著者,因此为买家提供了埃尔德什数为5的机会。一位西班牙数学家发布了1031美元的中标价格。不过他并不打算付款,而只是进行出价以阻止他认为是嘲弄的行为。<ref>Clifford A. Pickover: ''A Passion for Mathematics: Numbers, Puzzles, Madness, Religion, and the Quest for Reality''. Wiley, 2011, S. 33</ref><ref>{{cite journal | last1 = Klarreich | first1 = Erica | year = 2004 | title = Theorem for Sale | journal = Science News | volume = 165 | issue = 24| pages = 376–377 | doi = 10.2307/4015267 }}</ref> | ||
| − | + | ==演变== | |
| − | == 演变 == | ||
| − | |||
目前出现了很多对该概念进行变型的提议以应用于其他领域。 | 目前出现了很多对该概念进行变型的提议以应用于其他领域。 | ||
| − | |||
最著名的是游戏《与凯文·培根的六度分隔》中的培根数,将电影中出现的演员与演员凯文·培根联系在一起。它开始于1994年,距高夫曼关于埃尔德什数的文章发表25年。 | 最著名的是游戏《与凯文·培根的六度分隔》中的培根数,将电影中出现的演员与演员凯文·培根联系在一起。它开始于1994年,距高夫曼关于埃尔德什数的文章发表25年。 | ||
| − | |||
很少一部分人同时与埃尔德什和培根相连,因此有一个埃尔德什-培根数,该数通过求和将两个数相加。一个例子是女演员兼数学家丹妮卡·麦凯拉 Danica McKellar,她在电视连续剧《纯真年代》中扮演温妮·库珀而闻名。她的埃尔德什数是4,<ref>McKellar's co-author Lincoln Chayes published [https://projecteuclid.org/euclid.cmp/1103940982 a paper] with Elliott H. Lieb, who in turn co-authored [https://doi.org/10.1016/0012-365X(71)90004-5 a paper] with Daniel Kleitman, a co-author of Paul Erdős.</ref>她的培根数是2。<ref>Danica McKellar was in ''The Year That Trembled'' (2002) with James Kisicki, who was in ''Telling Lies in America'' (1997) with Kevin Bacon.</ref> | 很少一部分人同时与埃尔德什和培根相连,因此有一个埃尔德什-培根数,该数通过求和将两个数相加。一个例子是女演员兼数学家丹妮卡·麦凯拉 Danica McKellar,她在电视连续剧《纯真年代》中扮演温妮·库珀而闻名。她的埃尔德什数是4,<ref>McKellar's co-author Lincoln Chayes published [https://projecteuclid.org/euclid.cmp/1103940982 a paper] with Elliott H. Lieb, who in turn co-authored [https://doi.org/10.1016/0012-365X(71)90004-5 a paper] with Daniel Kleitman, a co-author of Paul Erdős.</ref>她的培根数是2。<ref>Danica McKellar was in ''The Year That Trembled'' (2002) with James Kisicki, who was in ''Telling Lies in America'' (1997) with Kevin Bacon.</ref> | ||
| − | |||
以此类推可以进一步扩展,例如,“埃尔德什-培根–萨巴什数”是“埃尔德什-培根数”在大众音乐领域与黑色安息日 Black Sabbath乐队的协作距离总和。物理学家斯蒂芬·霍金 Stephen Hawking的埃尔德什–培根–萨巴什数为8,<ref>{{cite web|url=https://www.timeshighereducation.com/blog/whats-your-erdos-bacon-sabbath-number |title=What's your Erdős–Bacon–Sabbath number? |website=Times Higher Education |date=2016-02-17 |access-date=2018-07-29 |last=Fisher |first=Len}}</ref> 女演员娜塔莉·波特曼 Natalie Portman的埃德斯–培根–萨巴什数为11(她的埃尔德什数为5)。<ref>{{cite web|url=http://blogs.surrey.ac.uk/physics/2012/09/15/erdos-bacon-sabbath-numbers/comment-page-1/ |title=Erdős–Bacon–Sabbath numbers |date=2012-09-15 |access-date=2018-07-29 |last=Sear |first=Richard |website=Department of Physics,University of Surrey}}</ref> | 以此类推可以进一步扩展,例如,“埃尔德什-培根–萨巴什数”是“埃尔德什-培根数”在大众音乐领域与黑色安息日 Black Sabbath乐队的协作距离总和。物理学家斯蒂芬·霍金 Stephen Hawking的埃尔德什–培根–萨巴什数为8,<ref>{{cite web|url=https://www.timeshighereducation.com/blog/whats-your-erdos-bacon-sabbath-number |title=What's your Erdős–Bacon–Sabbath number? |website=Times Higher Education |date=2016-02-17 |access-date=2018-07-29 |last=Fisher |first=Len}}</ref> 女演员娜塔莉·波特曼 Natalie Portman的埃德斯–培根–萨巴什数为11(她的埃尔德什数为5)。<ref>{{cite web|url=http://blogs.surrey.ac.uk/physics/2012/09/15/erdos-bacon-sabbath-numbers/comment-page-1/ |title=Erdős–Bacon–Sabbath numbers |date=2012-09-15 |access-date=2018-07-29 |last=Sear |first=Richard |website=Department of Physics,University of Surrey}}</ref> | ||
| − | |||
在国际象棋中,摩菲数描述了一个棋手与保罗·摩菲 Paul Morphy的联系,保罗·摩菲被广泛认为是他那个时代最伟大的棋手,也是非官方的第二位国际象棋国际象棋世界冠军。<ref>{{Cite web|last=Kingston|first=Taylor|title=Your Morphy Number Is Up|url=http://www.chesscafe.com/text/skittles258.pdf|url-status=live|archive-url=https://web.archive.org/web/20060613225534/http://www.chesscafe.com/text/skittles258.pdf|archive-date=13 June 2006|access-date=9 December 2020|website=Chesscafe}}</ref> | 在国际象棋中,摩菲数描述了一个棋手与保罗·摩菲 Paul Morphy的联系,保罗·摩菲被广泛认为是他那个时代最伟大的棋手,也是非官方的第二位国际象棋国际象棋世界冠军。<ref>{{Cite web|last=Kingston|first=Taylor|title=Your Morphy Number Is Up|url=http://www.chesscafe.com/text/skittles258.pdf|url-status=live|archive-url=https://web.archive.org/web/20060613225534/http://www.chesscafe.com/text/skittles258.pdf|archive-date=13 June 2006|access-date=9 December 2020|website=Chesscafe}}</ref> | ||
| − | + | ==参见== | |
| − | == 参见 == | ||
| − | |||
* 科学计量学 | * 科学计量学 | ||
* 小世界实验–检测社交网络平均路径长度的实验 | * 小世界实验–检测社交网络平均路径长度的实验 | ||
| 第250行: | 第208行: | ||
* 协作图–社交网络中的图建模协作 | * 协作图–社交网络中的图建模协作 | ||
| − | + | ==参考文献== | |
| − | ==参考文献 == | ||
{{reflist|colwidth=30em}} | {{reflist|colwidth=30em}} | ||
| − | + | ==相关链接== | |
| − | ==相关链接 == | ||
| − | |||
* Jerry Grossman, [http://www.oakland.edu/enp The Erdős Number Project]. Contains statistics and a complete list of all mathematicians with an Erdős number less than or equal to 2. | * Jerry Grossman, [http://www.oakland.edu/enp The Erdős Number Project]. Contains statistics and a complete list of all mathematicians with an Erdős number less than or equal to 2. | ||
| 第276行: | 第231行: | ||
* 数字视频. Ron Graham on imaginary Erdős numbers. | * 数字视频. Ron Graham on imaginary Erdős numbers. | ||
| − | |||
==编者推荐== | ==编者推荐== | ||
===集智文章=== | ===集智文章=== | ||
| − | + | *[https://swarma.org/?p=13508 小世界实验:六度分隔理论的来源 | 集智百科] | |
| − | + | ::Milgram的实验目的是为了研究两个随机选择的人之间相互认识的概率。这是看待小世界问题的一个角度。此问题的另外一种等价视角是将整个人群视作一个社交网络,然后尝试寻找任意两个节点之间的平均路径长度。Milgram的实验提供一套计算任何两个人之间的关联数的流程,用来测量这些路径的长度。 | |
| − | |||
| − | |||
| − | Milgram的实验目的是为了研究两个随机选择的人之间相互认识的概率。这是看待小世界问题的一个角度。此问题的另外一种等价视角是将整个人群视作一个社交网络,然后尝试寻找任意两个节点之间的平均路径长度。Milgram的实验提供一套计算任何两个人之间的关联数的流程,用来测量这些路径的长度。 | ||
| − | |||
'''基本流程:寄送包裹''' | '''基本流程:寄送包裹''' | ||
| − | |||
| − | |||
1.尽管实验存在许多变量,Milgram将通讯链的起点设置在美国的内布拉斯加州的奥马哈和堪萨斯州的威奇托,将终点设置在了马萨诸塞州的波士顿,并选取了这些城市的居民作为典型代表。选择这些城市的理由是人们认为他们无论在社会文化还是地理距离上都相距甚远。 | 1.尽管实验存在许多变量,Milgram将通讯链的起点设置在美国的内布拉斯加州的奥马哈和堪萨斯州的威奇托,将终点设置在了马萨诸塞州的波士顿,并选取了这些城市的居民作为典型代表。选择这些城市的理由是人们认为他们无论在社会文化还是地理距离上都相距甚远。 | ||
| − | |||
2.邮件包裹最初被“随机”发送给奥马哈和威奇托的居民,这些邮件包裹包括了标明研究目的的信件,和所要位于波士顿的目标联系人的基本信息。并附加了一份让参与者登记名字的花名册,以及寄回到哈佛的商用回邮信件。 | 2.邮件包裹最初被“随机”发送给奥马哈和威奇托的居民,这些邮件包裹包括了标明研究目的的信件,和所要位于波士顿的目标联系人的基本信息。并附加了一份让参与者登记名字的花名册,以及寄回到哈佛的商用回邮信件。 | ||
| − | |||
3.接收者被询问他或她是否认识信中描述的联系人。如果认识,那么信件将被直接交给目标联系人。基于实验目标,与某人私下认识被定义为与之关系密切(比如某些名人,大家都知道他们的名字,却不能算得上认识)。 | 3.接收者被询问他或她是否认识信中描述的联系人。如果认识,那么信件将被直接交给目标联系人。基于实验目标,与某人私下认识被定义为与之关系密切(比如某些名人,大家都知道他们的名字,却不能算得上认识)。 | ||
| − | |||
4.更可能的情况是,接收者并不认识目标联系人,那么这个人就需要考虑他的亲朋好友中谁更可能认识目标联系人。然后他们就在花名册上签下他们的名字。同时一张明信片就会寄回哈佛的研究者,以便他们能够追踪通讯的进展。 | 4.更可能的情况是,接收者并不认识目标联系人,那么这个人就需要考虑他的亲朋好友中谁更可能认识目标联系人。然后他们就在花名册上签下他们的名字。同时一张明信片就会寄回哈佛的研究者,以便他们能够追踪通讯的进展。 | ||
| − | |||
5.假如当包裹最终抵达了波士顿的目标联系人时,研究人员就可以检查花名册来记录它在人与人之间传递的次数。另外,如果包裹无法抵达目的地,寄回的明信片就能够标识出通讯链上的断点。 | 5.假如当包裹最终抵达了波士顿的目标联系人时,研究人员就可以检查花名册来记录它在人与人之间传递的次数。另外,如果包裹无法抵达目的地,寄回的明信片就能够标识出通讯链上的断点。 | ||
| + | [[File:swarma0-1544360416.gif |right|300px|thumb|一个可能的小世界实验的消息路线示意图(Stanley Milgram)]] | ||
| − | + | *[https://swarma.org/?p=13742 六度分隔实验的广泛影响 | 集智百科] | |
| − | + | ::当今,小世界问题仍旧是一个热门的研究主题,许多实验仍在持续开展中。比如,Peter Dodds,Roby Muhamad和Duncan Watts对Milgram的实验进行了首次大规模重复实验,其中包括24163封电子邮件通讯链和世界范围内的18位目标联系人。 | |
| − | |||
| − | 当今,小世界问题仍旧是一个热门的研究主题,许多实验仍在持续开展中。比如,Peter Dodds,Roby Muhamad和Duncan Watts对Milgram的实验进行了首次大规模重复实验,其中包括24163封电子邮件通讯链和世界范围内的18位目标联系人。 | ||
| − | |||
Dodds等人同时发现,即使考虑了误差,通讯链的平均长度也近似为六。卡梅隆大学( Carnegie Mellon University)做过一个基于受欢迎的社交网站的相似的实验。结果表明几乎没有消息能够真正抵达目的地。然而,米尔格拉姆所使用的方法也被用于这项研究。 | Dodds等人同时发现,即使考虑了误差,通讯链的平均长度也近似为六。卡梅隆大学( Carnegie Mellon University)做过一个基于受欢迎的社交网站的相似的实验。结果表明几乎没有消息能够真正抵达目的地。然而,米尔格拉姆所使用的方法也被用于这项研究。 | ||
| − | |||
'''网络模型''' | '''网络模型''' | ||
1998年,来自康奈尔大学的Duncan J. Watts和Steven Strogatz发表了小世界现象的第一个网络模型。他们揭示了,无论是自然界的还是人造世界中的网络,比如说秀丽隐杆线虫和输电网络,均展现出了小世界的特征。Watts和Strogatz发现,对于一个起始规则的网格,增加少量的随机边会降低直径——网络中的任意两点之间的最长的直接路径(direct path)——从很长变到很短。 | 1998年,来自康奈尔大学的Duncan J. Watts和Steven Strogatz发表了小世界现象的第一个网络模型。他们揭示了,无论是自然界的还是人造世界中的网络,比如说秀丽隐杆线虫和输电网络,均展现出了小世界的特征。Watts和Strogatz发现,对于一个起始规则的网格,增加少量的随机边会降低直径——网络中的任意两点之间的最长的直接路径(direct path)——从很长变到很短。 | ||
| − | |||
'''流行文化领域''' | '''流行文化领域''' | ||
社交网络充斥在美国和其它地区的流行文化中。特别地,六度的记号已经成为了集体意识(collective consciousness)的一部分。Facebook,Friendster,MySpace,XING,Orkut,Cyworld,Bebo一类的社交网站通过运用社交网络的理念,已经极大地增加了网络空间中的连通度。 | 社交网络充斥在美国和其它地区的流行文化中。特别地,六度的记号已经成为了集体意识(collective consciousness)的一部分。Facebook,Friendster,MySpace,XING,Orkut,Cyworld,Bebo一类的社交网站通过运用社交网络的理念,已经极大地增加了网络空间中的连通度。 | ||
| + | [[file:swarma7-1544965210.jpg|thumb|right|300px|来源:《NIPS2017上有关线虫对神经网络的启发》]] | ||
| + | |||
| + | *[https://swarma.org/?p=19627 什么是小世界网络模型 | 集智百科] | ||
| + | ::首先,我们需要了解小世界网络是一种数学图。在这种图中,绝大多数节点之间并不相邻,但任一给定节点的邻居们却很可能彼此相邻,并且大多数任意节点,都可以用较少的步或跳跃访问到其他节点。在社交网络中,这种网络属性意味着一些彼此并不相识的人,可以通过一条很短的熟人链条被联系在一起,这也就是小世界现象。许多经验网络图都展示出了小世界现象,例如社交网络、互联网的底层架构、诸如Wikipedia的百科类网站以及基因网络等等。 | ||
| − | |||
[[file:wxsync-2020-05-debf34cb1b84a732bda8e077255f047a.png|thumb|300px|right]] | [[file:wxsync-2020-05-debf34cb1b84a732bda8e077255f047a.png|thumb|300px|right]] | ||
| − | |||
| − | |||
| − | |||
===CSDN社区=== | ===CSDN社区=== | ||
| − | + | *[https://blog.csdn.net/weixin_34331102/article/details/90563756?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522162928221316780262520679%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=162928221316780262520679&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduend~default-2-90563756.first_rank_v2_pc_rank_v29&utm_term=%E5%9F%83%E5%B0%94%E5%BE%B7%E4%BB%80&spm=1018.2226.3001.4187 数学怪才埃尔德什] | |
| + | ---- | ||
| + | 本中文词条由[[用户:INCH RONG|Inch]]、[[用户:Jie|Jie]]、[[用户:Moonscar|Moonscar]]参与编译和审校,[[用户:唐糖糖|糖糖]]、SyouTK编辑,如有问题,欢迎在讨论页面留言。 | ||
| − | + | '''本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。''' | |
| − | |||
| − | |||
| − | |||
| + | [[category:社交网络]] | ||
| − | + | [[category:数学文献]] | |
2021年8月20日 (五) 16:42的版本
埃尔德什数 Erdős number(匈牙利语:[ˈɛrdøːʃ])根据数学论文的著作权来来对数学家保罗·埃尔德什与其他作者之间的“协作距离”进行描述。同样的原则也应用于很多当特定某个人与众多同行之间保持合作关系的其他领域。
概况
保罗·埃尔德什 Paul Erdős(1913年至1996年)是一位在业界产生有影响力的匈牙利数学家,其一生中大量的时间都在与很多同事合作撰写论文,致力于解决困扰已久的疑难数学问题。[1] 他一生中所发表的论文(至少1,525篇[2])比历史上其他任何数学家都多[1]。莱昂哈德·欧拉 Leonhard Euler发表过的数学论文页数更多,但单独的论文却较少(大约800篇)。[3]而埃尔德什的大部分时间都在旅居中,其拜访过全球500多个合作者。
埃尔德什数的概念最初是由埃尔德什的朋友们提出来的,以赞扬保罗·埃尔德什的巨大成就。后来,它演变为研究数学家如何通过合作来解决问题的的工具而受到重视。有几个项目致力于使用埃尔德什数为代表方法来研究人员之间的连通性。[4]例如,埃尔德什合作图可以告诉我们作者是如何聚集在一起的,每篇论文的共同作者数量随时间变化或新理论的产生如何传播的。[5]
多项研究表明,领先的数学家往往具有极低的埃尔德什数。[6]菲尔兹奖得主Fields Medalists的埃尔德什中位数是3。只有7,097名(拥有合作经历的数学家中约5%)的埃尔德什数为2或更低。随着时间的流逝,低埃尔德什数的数学家因死亡而无法进行协作,所能达到的最小埃尔德什数必然会增加。历史人物仍可能一直具有较低的埃尔德什数。例如,印度著名数学家Srinivasa Ramanujan的埃尔德什数仅为3(通过与G. H. Hardy合作,其埃尔德什数为2),尽管Ramanujan去世时保罗·埃尔德什只有7岁。[7] [8]
数学的定义与应用
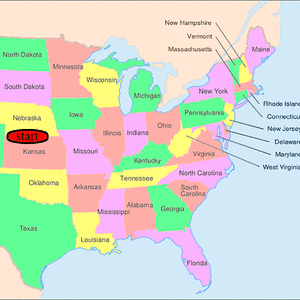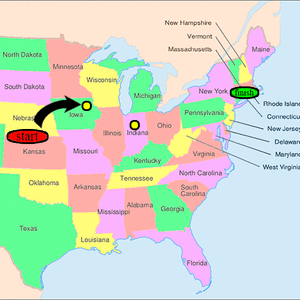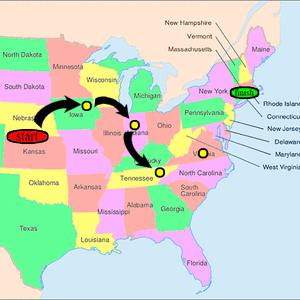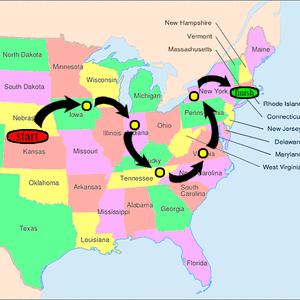
要分配一个埃尔德什数,某人必须与另一个具有有限埃尔德什数的人共同撰写研究论文。保罗·埃尔德什的埃尔德什数为零。其他人的埃尔德什数为k+1,其中k是任何合著者中最低的埃尔德什数。美国数学学会提供免费的在线工具来确定《数学评论》目录中列出的每个数学作者的埃尔德什数。[8]
埃尔德什一生撰写了约1500篇数学文章,其中大部分是合作的。他有511个直接合作者[4];这些是埃尔德什数为1的人。与这些人合作(但未与埃尔德什本人合作)的人所拥有的埃尔德什数为2(截至2020年8月7日为12,600人[9]),而与埃尔德什数为2的人合作的人(但与埃尔德什或埃尔德什数为1的任何人无合作关系),其埃尔德什数为3,依此类推。没有此类共同作者链接能指向埃尔德什的人,其埃尔德什数为无穷大(或未定义)。自保罗·埃尔德什逝世以来,新研究员可获得的最低埃尔德什数为2。
关于具体由什么构成两位作者之间的联系,众说纷纭。美国数学学会的“协作距离计算器”使用的是来自《数学评论》的数据,包括大多数数学期刊,但仅以有限的方式涵盖了其他主题,同时还包括一些非研究出版物。埃尔德什数项目官方网站Erdős Number Project表示:
...我们在顶点u和v之间共有的包含边标准是,它们之间的某些研究合作导致了发表的作品。任何数量的其他共同作者都是被允许的,...
但它们不包括非研究性出版物,例如教科书,联合编辑,讣告等。“第二种埃尔德什数”将其分配给只有两个合作者的论文。[10]
埃尔德什数很可能最早由卡斯珀·高夫曼 Casper Goffman定义,他自己的埃尔德什数为2。[9]高夫曼在1969年发表的一篇文章“您的埃尔德什数是多少”中表示了他对埃尔德什多产合作的看法[11],另请参阅迈克尔·哥伦布 Michael Golomb在讣告中的一些评论。[12]
菲尔兹奖获得者的埃尔德什中位数低至3。[7]埃尔德什排名第二的奖牌获得者包括Atle Selberg,Kunihiko Kodaira,Klaus Roth,Alan Baker,Enrico Bombieri,David Mumford,Charles Fefferman,William Thurston,Shing-Tung Tung,Jean Bourgain,Richard Borcherds,Manjul Bhargava,Jean-Pierre Serre和陶哲轩。菲尔兹奖获得者中没有人的埃尔德什数为1。[13]但是,恩德雷·塞梅雷迪 Endre Szemerédi是阿贝尔奖获得者,其埃尔德什数为1。[6]
最频繁的埃尔德什合作者
虽然埃尔德什与数百位合著者合作,但其中一些人与他合作过数十篇论文。以下是最经常与埃尔德什合作的十人列表,以及与埃尔德什合作的论文数量(即合作数量)。[14]
| 合著者 | 合作 数量 |
|---|---|
| András Sárközy | 62 |
| András Hajnal | 56 |
| Ralph Faudree | 50 |
| Richard Schelp | 42 |
| Cecil C. Rousseau | 35 |
| Vera T. Sós | 35 |
| Alfréd Rényi | 32 |
| Pál Turán | 30 |
| Endre Szemerédi | 29 |
| Ronald Graham | 28 |
相关领域
截至2016年,所有菲尔兹奖章获得者都有一个有限的埃尔德什数,其值在2到6之间,中位数为3。相反,所有数学家的埃尔德什数的中位数(有限的埃尔德什数)为5,极限值为13。[15]下表总结了物理,化学,医学和经济学方面的诺贝尔奖得主的埃尔德什数统计。[16]第一列计算获奖人数。第二列计算的是具有有限埃尔德什数的获胜者数量。第三列是具有有限埃尔德什数的获胜者的百分比。其余各列表示了这些获奖者中埃尔德什数的最小,最大,平均和中位数。
| 获奖人数 | 有限埃尔德什数 获胜者数量 |
有限埃尔德什数 获胜者百分比 |
最小埃尔德什数 | 最大埃尔德什数 | 平均埃尔德什数 | 中位埃尔德什数 | |
|---|---|---|---|---|---|---|---|
| 菲尔兹奖 | 56 | 56 | 100.0% | 2 | 6 | 3.36 | 3 |
| 诺贝尔经济学奖 | 76 | 47 | 61.84% | 2 | 8 | 4.11 | 4 |
| 诺贝尔化学奖 | 172 | 42 | 24.42% | 3 | 10 | 5.48 | 5 |
| 诺贝尔 生理学或医学奖 |
210 | 58 | 27.62% | 3 | 12 | 5.50 | 5 |
| 诺贝尔物理学奖 | 200 | 159 | 79.50% | 2 | 12 | 5.63 | 5 |
物理领域
在诺贝尔物理学奖获得者中,爱因斯坦 Albert Einstein和谢尔登·李·格拉肖 Sheldon Lee Glashow的埃尔德什数为2。诺贝尔奖获得者中埃尔德什数为3的有: Enrico Fermi,Otto Stern,Wolfgang Pauli,Max Born,Willis E.Lamb,Eugene Wigner,Richard P.Feynman,Hans A.Bethe,Murray Gell-Mann,Abdus Salam,Steven Weinberg,Norman F.Ramsey,Frank Wilczek和David Wineland。获得菲尔兹奖的物理学家Ed Witten的埃尔德什数为3。[7]
生物学领域
计算生物学家Lior Pachter的埃尔德什数为2。[17]进化生物学家Richard Lenski的埃尔德什数为3,与Lior Pachter和数学家Bernd Sturmfels共同撰写了出版物的每位作者埃尔德什数为2。[18]
财经领域
至少有两名诺贝尔经济学奖获得者的埃尔德什数为2:哈里·马可维兹 Harry M. Markowitz,(1990)和列昂尼德·坎托罗维奇 Leonid Kantorovich(1975)。埃尔德什数为2的其他金融数学家包括David Donoho,Marc Yor,Henry McKean,Daniel Stroock和Joseph Keller。
埃尔德什数为3的诺贝尔经济学奖得主,其中包括Kenneth J. Arrow(1972),Milton Friedman(1976),Herbert A. Simon(1978),Gerard Debreu(1983),John Forbes Nash,Jr.(1994),James Mirrlees(1996),Daniel McFadden(2000),Daniel Kahneman(2002),Robert J.Aumann(2005),Leonid Hurwicz(2007),Roger Myerson(2007),Alvin E.Roth(2012)和Lloyd S. Shapley(2012)和Jean Tirole(2014)。[19]
一些埃尔德什数低的数学家创立了投资公司,其中包括Axcom Technologies的James B. Ax和Renaissance Technologies的James H. Simons,两者的埃尔德什数均为3。[20][21]
哲学领域
由于哲学的本质与数学基础缘由互通,因此它们有很多重叠的地方,许多哲学家都可以使用埃尔德什数。[22]哲学家John P. Burgess的埃尔德什数为2。[17]Barwise和Joel David Hamkins埃尔德什数都为2,他们为哲学做出了大量贡献,但通常被称为数学家。
法律领域
与Alvin E. Roth合作的法官Richard Posner的埃尔德什数最多为4。在哈佛法学院任教的政治家,哲学家和法律理论家Roberto Mangabeira Unger与Lee Smolin曾经合作过,其埃尔德什数最多为4。
政治领域
从2005年至今的德国总理安格拉·默克尔 Angela Merkel的埃尔德什数最多为5。[13]
工程领域
工程的某些领域,尤其是通信理论和密码学,直接利用了埃尔德什数主要涉及的离散数学。因此,这些领域的从业人员的埃尔德什数低就不足为奇了。例如,加州理工学院电气工程学教授Robert McEliece与埃尔德什本人合作,其埃尔德什数为1。[23]RSA密码系统的发明者,密码学家Ron Rivest,Adi Shamir和Leonard Adleman的埃尔德什数均为2。[17]
社交网络分析领域
人类学家道格拉斯·怀特 Douglas R. White通过与图论家弗兰克·哈拉里 Frank Harary合作得到埃尔德什数为2。[24][25]社会学家巴里·韦尔曼 Barry Wellman通过与社交网络分析师和统计学家 Ove Frank[26](Harve's的另一位合作者)[27]合作得到了埃尔德什数为3。
语言学领域
罗马尼亚数学家和计算语言学家Solomon Marcus在1957年与埃尔德什合作了《 Acta Mathematica Hungarica》中的一篇论文,因此他的埃尔德什数为1。[28]
影响
多年以来,埃尔德什数在数学家之间一直盛行。在千年之交的所有在职数学家中,都伴随着一个有限埃尔德什数,数字范围最大为15,中位数为5,平均值为4.65。[4]几乎每个具有有限埃尔德什数的人其数字都小于8。由于当今科学领域跨学科合作的频率很高,因此许多其他科学领域的大量非数学家也具有有限的埃尔德什数。[29]例如,政治学家Steven Brams的埃尔德什数为2。在生物医学研究中,统计学家通常是出版物的作者,许多统计学家可以通过John Tukey(其埃尔德什数为2)与埃尔德什链接。同样,著名的遗传学家Eric Lander和数学家Daniel Kleitman在论文上进行了合作,[30][31]由于Kleitman的埃尔德什数为1,[32]因此可以通过Lander及其众多合作者将遗传学和基因组学领域的大部分联系起来。另外,与Gustavus Simmons的合作为密码研究界内的埃尔德什数打开了大门,许多语言学家拥有有限的埃尔德什数,这许多是由于与Noam Chomsky(埃尔德什数为4),[33]William Labov(埃尔德什数为3)等著名学者的合作产生,[34]类似有Mark Liberman(3)[35] ,Geoffrey Pullum(3)[36]或Ivan Sag(4)[37]。同时与艺术领域也有联系。[38]
根据亚历克斯·洛佩兹·奥尔蒂斯 Alex Lopez-Ortiz的说法,在1986年至1994年的三个周期中,所有菲尔兹奖和内凡琳娜奖 Nevanlinna prize得主的埃尔德什数最多为9。
较早的数学家发表的论文通常少于现代的,而且很少发表联合论文。已知拥有有限埃尔德什数的最早学者是Antoine Lavoisier(生于1743年,埃尔德什数为13),Richard Dedekind(生于1831年,埃尔德什数为7)或Ferdinand Georg Frobenius(生于1849年,埃尔德什数为3),具体取决于出版物资格标准。[39]
马丁·汤帕 Martin Tompa[40] 提出了埃尔德什数问题的有向图版本,通过定向协作图,将字母顺序更早的作者到字母顺序更晚的作者进行排列,并将作者的单调埃尔德什数定义为该有向图中从埃尔德什到作者的最长路径的长度。他发现这种路径长度为12。
另外,迈克尔·巴尔 Michael Barr曾建议使用“合理的埃尔德什数”,通俗的说就是与埃尔德共同撰写过p篇论文的人应被分配埃尔德什数的1/p。根据第二种的协作多重图(尽管他也有办法处理第一种情况),即在他们所合著的每篇联合论文中,两个数学家之间都有一条边,我们可以将其视为这个网络视每一条边上都有一个1欧姆电阻器的电网。两个节点之间的总电阻表明这两个节点有多“相近”。
有人提出:“对于独立研究人员而言,诸如埃尔德什数之类的量度可以捕获网络的结构特性,而h指数则可以捕获出版物的引文影响。” 并且“可以很容易地使人相信,共同作者网络中的排名应该同时考虑到两种方法,以产生现实且可接受的排名。”[41]
2004年,数学家埃尔德什数为4的William Tozier在eBay上拍卖了合著者,因此为买家提供了埃尔德什数为5的机会。一位西班牙数学家发布了1031美元的中标价格。不过他并不打算付款,而只是进行出价以阻止他认为是嘲弄的行为。[42][43]
演变
目前出现了很多对该概念进行变型的提议以应用于其他领域。
最著名的是游戏《与凯文·培根的六度分隔》中的培根数,将电影中出现的演员与演员凯文·培根联系在一起。它开始于1994年,距高夫曼关于埃尔德什数的文章发表25年。
很少一部分人同时与埃尔德什和培根相连,因此有一个埃尔德什-培根数,该数通过求和将两个数相加。一个例子是女演员兼数学家丹妮卡·麦凯拉 Danica McKellar,她在电视连续剧《纯真年代》中扮演温妮·库珀而闻名。她的埃尔德什数是4,[44]她的培根数是2。[45]
以此类推可以进一步扩展,例如,“埃尔德什-培根–萨巴什数”是“埃尔德什-培根数”在大众音乐领域与黑色安息日 Black Sabbath乐队的协作距离总和。物理学家斯蒂芬·霍金 Stephen Hawking的埃尔德什–培根–萨巴什数为8,[46] 女演员娜塔莉·波特曼 Natalie Portman的埃德斯–培根–萨巴什数为11(她的埃尔德什数为5)。[47]
在国际象棋中,摩菲数描述了一个棋手与保罗·摩菲 Paul Morphy的联系,保罗·摩菲被广泛认为是他那个时代最伟大的棋手,也是非官方的第二位国际象棋国际象棋世界冠军。[48]
参见
- 科学计量学
- 小世界实验–检测社交网络平均路径长度的实验
- 小世界网络–可通过较少步数到达大多数节点的数字图
- 六度分离–所有人之间社会联系
- 科学知识社会学–将科学作为一种社会活动的研究
- 按埃尔德什数列出的人员列表–维基百科列表文章
- 以保罗·埃尔德什命名的清单–维基百科清单文章
- 协作图–社交网络中的图建模协作
参考文献
- ↑ 1.0 1.1 Newman, Mark E. J. (2001). "The structure of scientific collaboration networks". Proceedings of the National Academy of Sciences of the United States of America. 98 (2): 404–409. doi:10.1073/pnas.021544898. PMC 14598. PMID 11149952.
- ↑ Grossman, Jerry. "Publications of Paul Erdős". Retrieved 1 Feb 2011.
- ↑ "Frequently Asked Questions". The Euler Archive. Dartmouth College.
- ↑ 4.0 4.1 4.2 "Erdös Number Project". Oakland University.
- ↑ "Facts about Erdös Numbers and the Collaboration Graph". Erdös Number Project. Oakland University.
- ↑ 6.0 6.1 De Castro, Rodrigo; Grossman, Jerrold W. (1999). "Famous trails to Paul Erdős" (PDF). The Mathematical Intelligencer. 21 (3): 51–63. doi:10.1007/BF03025416. Archived from the original (PDF) on 2015-09-24. Original Spanish version in Rev. Acad. Colombiana Cienc. Exact. Fís. Natur. 23 (89) 563–582, 1999.
- ↑ 7.0 7.1 7.2 "Some Famous People with Finite Erdős Numbers". oakland.edu. Retrieved 4 April 2014.
- ↑ 8.0 8.1 "Collaboration Distance". MathSciNet. American Mathematical Society.
- ↑ 9.0 9.1 Erdos2, Version 2020, 7 August 2020.
- ↑ Grossman et al. "Erdős numbers of the second kind," in Facts about Erdős Numbers and the Collaboration Graph. The Erdős Number Project, Oakland University, USA. Retrieved July 25, 2009.
- ↑ Goffman, Casper (1969). "And what is your Erdős number?". American Mathematical Monthly. 76 (7): 791. doi:10.2307/2317868.
- ↑ "Paul Erdös at Purdue". www.math.purdue.edu.
- ↑ 13.0 13.1 "Paths to Erdös". The Erdös Number Project. Oakland University.
- ↑ Grossman, Jerry, Erdos0p, Version 2010, The Erdős Number Project, Oakland University, US, October 20, 2010.
- ↑ "Facts about Erdös Numbers and the Collaboration Graph - The Erdös Number Project- Oakland University". wwwp.oakland.edu. Retrieved 2016-10-27.
- ↑ López de Prado, Marcos (2016). "Mathematics and Economics: A reality check". The Journal of Portfolio Management. 43 (1): 5–8. doi:10.3905/jpm.2016.43.1.005.
- ↑ 17.0 17.1 17.2 "List of all people with Erdos number less than or equal to 2". The Erdös Number Project. Oakland University. 14 July 2015. Retrieved 25 August 2015.
- ↑ Richard Lenski (May 28, 2015). "Erdös with a non-kosher side of Bacon".
- ↑ Grossman, J. (2015): "The Erdős Number Project." http://wwwp.oakland.edu/enp/erdpaths/
- ↑ Kishan, Saijel (2016-11-11). "Six Degrees of Quant: Kevin Bacon and the Erdős Number Mystery". Bloomberg.com. Retrieved 2016-11-12.
- ↑ Bailey, David H. (2016-11-06). "Erdős Numbers: A True "Prince and the Pauper" story". The Mathematical Investor (in English). Retrieved 2016-11-12.
- ↑ Toby Handfield. "Philosophy research networks" (PDF). Archived from the original (PDF) on 2016-02-21.
- ↑ Erdős, Paul, Robert McEliece, and Herbert Taylor (1971). "Ramsey bounds for graph products" (PDF). Pacific Journal of Mathematics. 37 (1): 45–46. doi:10.2140/pjm.1971.37.45.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ White, Douglas R.; Harary, Frank (2001). "The Cohesiveness of Blocks in Social Networks: Node Connectivity and Conditional Density". Sociological Methodology. 31: 305–59. doi:10.1111/0081-1750.00098.
- ↑ "VITA: Douglas R.White, Anthropology & Social Science Professor, UC-Irvine". Retrieved December 14, 2017.
- ↑ Barry Wellman, Ove Frank, Vicente Espinoza, Staffan Lundquist and Craig Wilson. "Integrating Individual, Relational and Structural Analysis". 1991. Social Networks 13 (Sept.): 223-50.
- ↑ Ove Frank; Frank Harary, "Cluster Inference by Using Transitivity Indices in Empirical Graphs." Journal of the American Statistical Association, 77, 380. (Dec., 1982), pp. 835–840.
- ↑ Erdős, Paul; Marcus, Solomon (1957). "Sur la décomposition de l'espace euclidien en ensembles homogènes" [On the decomposition of the Euclidean space into homogeneous sets]. Acta Mathematica Hungarica. 8 (3–4): 443–452. doi:10.1007/BF02020326.
- ↑ Grossman, Jerry. "Some Famous People with Finite Erdős Numbers". Retrieved 1 February 2011.
- ↑ Pachter, L; Batzoglou, S; Spitkovsky, VI; Banks, E; Lander, ES; Kleitman, DJ; Berger, B (1999). "A dictionary-based approach for gene annotation". J Comput Biol. 6 (3–4): 419–30. doi:10.1089/106652799318364. PMID 10582576.
- ↑ Kleitman, Daniel. "Publications Since 1980 more or less". Massachusetts Institute of Technology.
- ↑ Erdős, Paul; Kleitman, Daniel (April 1971). "On Collections of Subsets Containing No 4-Member Boolean Algebra" (PDF). Proceedings of the American Mathematical Society. 28 (1): 87–90. doi:10.2307/2037762.
- ↑ von Fintel, Kai (2004). "My Erdös Number is 8". Semantics, Inc. Archived from the original on 23 August 2006.
- ↑ "Aaron Dinkin has a web site?". Ling.upenn.edu. Retrieved 2010-08-29.
- ↑ "Mark Liberman's Home Page". Ling.upenn.edu. Retrieved 2010-08-29.
- ↑ "Christopher Potts: Miscellany". Stanford.edu. Retrieved 2010-08-29.
- ↑ "Bob's Erdős Number". Lingo.stanford.edu. Retrieved 2010-08-29.
- ↑ Bowen, Jonathan P.; Wilson, Robin J. (10–12 July 2012). "Visualising Virtual Communities: From Erdős to the Arts". In Dunn, Stuart; Bowen, Jonathan P.; Ng, Kia (eds.). EVA London 2012: Electronic Visualisation and the Arts. Electronic Workshops in Computing. British Computer Society. pp. 238–244.
- ↑ "Paths to Erdös - The Erdös Number Project- Oakland University". oakland.edu.
- ↑ Tompa, Martin (1989). "Figures of merit". ACM SIGACT News. 20 (1): 62–71. doi:10.1145/65780.65782. Tompa, Martin (1990). "Figures of merit: the sequel". ACM SIGACT News. 21 (4): 78–81. doi:10.1145/101371.101376.
- ↑ Kashyap Dixit, S Kameshwaran, Sameep Mehta, Vinayaka Pandit, N Viswanadham, Towards simultaneously exploiting structure and outcomes in interaction networks for node ranking, IBM Research Report R109002, February 2009; also appeared as Kameshwaran, S.; Pandit, V.; Mehta, S.; Viswanadham, N.; Dixit, K. (2010). "Outcome aware ranking in interaction networks" (PDF). Proceedings of the 19th ACM International Conference on Information and Knowledge Management (CIKM '10): 229–238. doi:10.1145/1871437.1871470.
- ↑ Clifford A. Pickover: A Passion for Mathematics: Numbers, Puzzles, Madness, Religion, and the Quest for Reality. Wiley, 2011, S. 33
- ↑ Klarreich, Erica (2004). "Theorem for Sale". Science News. 165 (24): 376–377. doi:10.2307/4015267.
- ↑ McKellar's co-author Lincoln Chayes published a paper with Elliott H. Lieb, who in turn co-authored a paper with Daniel Kleitman, a co-author of Paul Erdős.
- ↑ Danica McKellar was in The Year That Trembled (2002) with James Kisicki, who was in Telling Lies in America (1997) with Kevin Bacon.
- ↑ Fisher, Len (2016-02-17). "What's your Erdős–Bacon–Sabbath number?". Times Higher Education. Retrieved 2018-07-29.
- ↑ Sear, Richard (2012-09-15). "Erdős–Bacon–Sabbath numbers". Department of Physics,University of Surrey. Retrieved 2018-07-29.
- ↑ Kingston, Taylor. "Your Morphy Number Is Up" (PDF). Chesscafe. Archived (PDF) from the original on 13 June 2006. Retrieved 9 December 2020.
相关链接
- Jerry Grossman, The Erdős Number Project. Contains statistics and a complete list of all mathematicians with an Erdős number less than or equal to 2.
- "On a Portion of the Well-Known Collaboration Graph", Jerrold W. Grossman and Patrick D. F. Ion.
- "Some Analyses of Erdős Collaboration Graph", Vladimir Batagelj and Andrej Mrvar.
- American Mathematical Society, [1]. A search engine for Erdős numbers and collaboration distance between other authors. As of 18 November 2011 no special access is required.
- Numberphile video. Ron Graham on imaginary Erdős numbers.
- Jerry Grossman,《埃尔德什数项目》.统计数据以及埃尔德什数小于或等于2的所有数学家的完整列表.
- "著名协作图的分配", Jerrold W. Grossman and Patrick D. F. Ion.
- "埃尔德什协作图的部分分析", Vladimir Batagelj and Andrej Mrvar.
- American Mathematical Society, [1]. 计算埃尔德什数和其他作者之间协作距离的搜索引擎. As of 18 November 2011 no special access is required.
- 数字视频. Ron Graham on imaginary Erdős numbers.
编者推荐
集智文章
- Milgram的实验目的是为了研究两个随机选择的人之间相互认识的概率。这是看待小世界问题的一个角度。此问题的另外一种等价视角是将整个人群视作一个社交网络,然后尝试寻找任意两个节点之间的平均路径长度。Milgram的实验提供一套计算任何两个人之间的关联数的流程,用来测量这些路径的长度。
基本流程:寄送包裹 1.尽管实验存在许多变量,Milgram将通讯链的起点设置在美国的内布拉斯加州的奥马哈和堪萨斯州的威奇托,将终点设置在了马萨诸塞州的波士顿,并选取了这些城市的居民作为典型代表。选择这些城市的理由是人们认为他们无论在社会文化还是地理距离上都相距甚远。
2.邮件包裹最初被“随机”发送给奥马哈和威奇托的居民,这些邮件包裹包括了标明研究目的的信件,和所要位于波士顿的目标联系人的基本信息。并附加了一份让参与者登记名字的花名册,以及寄回到哈佛的商用回邮信件。
3.接收者被询问他或她是否认识信中描述的联系人。如果认识,那么信件将被直接交给目标联系人。基于实验目标,与某人私下认识被定义为与之关系密切(比如某些名人,大家都知道他们的名字,却不能算得上认识)。
4.更可能的情况是,接收者并不认识目标联系人,那么这个人就需要考虑他的亲朋好友中谁更可能认识目标联系人。然后他们就在花名册上签下他们的名字。同时一张明信片就会寄回哈佛的研究者,以便他们能够追踪通讯的进展。
5.假如当包裹最终抵达了波士顿的目标联系人时,研究人员就可以检查花名册来记录它在人与人之间传递的次数。另外,如果包裹无法抵达目的地,寄回的明信片就能够标识出通讯链上的断点。
- 当今,小世界问题仍旧是一个热门的研究主题,许多实验仍在持续开展中。比如,Peter Dodds,Roby Muhamad和Duncan Watts对Milgram的实验进行了首次大规模重复实验,其中包括24163封电子邮件通讯链和世界范围内的18位目标联系人。
Dodds等人同时发现,即使考虑了误差,通讯链的平均长度也近似为六。卡梅隆大学( Carnegie Mellon University)做过一个基于受欢迎的社交网站的相似的实验。结果表明几乎没有消息能够真正抵达目的地。然而,米尔格拉姆所使用的方法也被用于这项研究。
网络模型 1998年,来自康奈尔大学的Duncan J. Watts和Steven Strogatz发表了小世界现象的第一个网络模型。他们揭示了,无论是自然界的还是人造世界中的网络,比如说秀丽隐杆线虫和输电网络,均展现出了小世界的特征。Watts和Strogatz发现,对于一个起始规则的网格,增加少量的随机边会降低直径——网络中的任意两点之间的最长的直接路径(direct path)——从很长变到很短。
流行文化领域 社交网络充斥在美国和其它地区的流行文化中。特别地,六度的记号已经成为了集体意识(collective consciousness)的一部分。Facebook,Friendster,MySpace,XING,Orkut,Cyworld,Bebo一类的社交网站通过运用社交网络的理念,已经极大地增加了网络空间中的连通度。
- 首先,我们需要了解小世界网络是一种数学图。在这种图中,绝大多数节点之间并不相邻,但任一给定节点的邻居们却很可能彼此相邻,并且大多数任意节点,都可以用较少的步或跳跃访问到其他节点。在社交网络中,这种网络属性意味着一些彼此并不相识的人,可以通过一条很短的熟人链条被联系在一起,这也就是小世界现象。许多经验网络图都展示出了小世界现象,例如社交网络、互联网的底层架构、诸如Wikipedia的百科类网站以及基因网络等等。
CSDN社区
本中文词条由Inch、Jie、Moonscar参与编译和审校,糖糖、SyouTK编辑,如有问题,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。