“约翰·何顿·康威 John Horton Conway”的版本间的差异

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
跳到导航 跳到搜索
第348行： 第348行：
  
 
[https://www.math.princeton.edu/people/john-conway 普林斯顿大学数学系个人主页]
 
[https://www.math.princeton.edu/people/john-conway 普林斯顿大学数学系个人主页]
 +
 +
==参考文献==
 +
<references/>
  
 
----
 
----

2020年4月12日 (日) 11:57的版本


约翰·霍顿·康威 John Horton Conway [1]（生于1937年12月26日，<！-死因尚未得到可靠来源的证实->）是一位活跃于有限群 finite groups理论的英国数学家，纽结理论 knot theory，数论 number theory，组合博弈论 combinatorial game theory和编码论 coding theory。 他还为趣味数学 recreational mathematics的许多分支做出了贡献，其中最著名的是元胞自动机 Cellular Automata的发明，康威的生命游戏。 康威（Conway）先是在英国剑桥大学度过他一半的职业生涯，而在新泽西普林斯顿大学的新泽西州度过了下半场职业生涯，他获得了John von Neumann荣誉教授的头衔。 .[2][3][4][5][6][7][8]


基本信息

J.H conway.jpg
类别 信息
姓名： 约翰·何顿·康威John Horton Conway
出生日期： 1937年12月26日
出生地： 英国默西赛德郡利物浦
国籍： 英国
居住地： 美国
母校： 剑桥大学
成就： 康威的生命游戏 Conway's Game of Life , 外观数列
主要研究方向： 有限群理论、纽结理论、数论、组合博弈论和编码理论


教育和早期生活

康威（Conway）生于Liverpool[9]，是西里尔·霍顿·康威 （Cyril Horton Conway） 和艾格尼丝·博伊斯（Agnes Boyce）的儿子。[10][8]他从很小的时候就对数学感兴趣。到11岁时，他的志向是成为一名数学家。

离开六年级后，康威进入了剑桥的冈维尔和凯斯学院 学习数学。[10]康威（Conway）在学校时是一个“非常内向的青少年”，他将自己进入剑桥的机会解释为将自己转变为一个新人的机会：一个“外向的人”。[11][12]

他于1959年获得文学学士学位，并在Harold Davenport的指导下开始进行数论研究。解决了达文波特对华林问题（每个足够大的整数可以表示为最多16个四次方的总和）提出的开放问题，康威开始对无限序数感兴趣。似乎他对游戏的兴趣始于他研究Cambridge Mathematical Tripos的岁月，在那里他成为了一个狂热的西洋双陆棋 Backgammon玩家，花了数小时在休息室里玩游戏。他于1964年获得博士学位，并被Sidney Sussex College，Cambridge任命为大学研究员和数学讲师。

1986年离开剑桥后，他被任命为普林斯顿大学数学John von Neumann主席。

康威生命游戏简介

Conway的人生游戏：单个的（细胞自动机）滑翔机枪

康威（Conway）以生命游戏的发明而闻名，生命游戏是元胞自动机 Cellular Automata的早期实例之一。他在该领域的最初实验是使用笔和纸完成的，远早于个人计算机的出现。

自1970年马丁·加德纳（Martin Gardner）在“ Scientific American”中推出游戏以来，[13]它产生了数百个计算机程序，网站和文章。[14] 它是趣味数学的主要内容。有大量的wiki专门用于管理和分类游戏的各个方面。 [15]在理论上以及在编程和数据显示方面的实践活动一直是计算机实验室的最爱。[16] 康威有时说他讨厌生命游戏，很大程度上是因为它掩盖了他所做的其他一些更深入，更重要的事情。不过，该游戏确实帮助启动了一个新的数学分支，即元胞自动机 Cellular Automata领域。[17] 生命游戏现在被称为“图灵完备 Turing completeness”。[18][19]

游戏规则

  • 任何四周邻居存活数少于两个的存活网格将死亡，因为人口稀少。
  • 任何四周邻居存活数多于三个的存活网格将死亡，因为过度拥挤。
  • 任何四周邻居存活数等于两个或三个的存活网格将在下一代中继续存活。
  • 任何已经死亡的网格，如果周围邻居存活数为3个，将重新复活。

康威生命游戏python 实现

康威生命游戏python 实现下载: 

"""
conway.py 
A simple Python/matplotlib implementation of Conway's Game of Life.
Author: Mahesh Venkitachalam
"""

import sys, argparse
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation

ON = 255
OFF = 0
vals = [ON, OFF]


def randomGrid(N):
    """随机产生"""
    return np.random.choice(vals, N * N, p=[0.2, 0.8]).reshape(N, N)


def addGlider(i, j, grid):
    """添加一个滑翔机"""
    glider = np.array([[0, 0, 255],
                       [255, 0, 255],
                       [0, 255, 255]])
    grid[i:i + 3, j:j + 3] = glider


def addGosperGliderGun(i, j, grid):
    """添加一个滑翔机发射器"""
    gun = np.zeros(11 * 38).reshape(11, 38)

    gun[5][1] = gun[5][2] = 255
    gun[6][1] = gun[6][2] = 255

    gun[3][13] = gun[3][14] = 255
    gun[4][12] = gun[4][16] = 255
    gun[5][11] = gun[5][17] = 255
    gun[6][11] = gun[6][15] = gun[6][17] = gun[6][18] = 255
    gun[7][11] = gun[7][17] = 255
    gun[8][12] = gun[8][16] = 255
    gun[9][13] = gun[9][14] = 255

    gun[1][25] = 255
    gun[2][23] = gun[2][25] = 255
    gun[3][21] = gun[3][22] = 255
    gun[4][21] = gun[4][22] = 255
    gun[5][21] = gun[5][22] = 255
    gun[6][23] = gun[6][25] = 255
    gun[7][25] = 255

    gun[3][35] = gun[3][36] = 255
    gun[4][35] = gun[4][36] = 255

    grid[i:i + 11, j:j + 38] = gun


def update(frameNum, img, grid, N):
    """
    根据游戏规则刷新图像
    :param frameNum: matplotlib.animation模块需要传入的数据
    :param img: 原图
    :param grid: 坐标
    :param N: 尺寸
    :return: 新图
    """
    newGrid = grid.copy()
    for i in range(N):
        for j in range(N):
            # 计算周围八个格的和（0，255），计算周围有多少生命
            # %N用于考虑边界条件
            total = int((grid[i, (j - 1) % N] + grid[i, (j + 1) % N] +
                         grid[(i - 1) % N, j] + grid[(i + 1) % N, j] +
                         grid[(i - 1) % N, (j - 1) % N] + grid[(i - 1) % N, (j + 1) % N] +
                         grid[(i + 1) % N, (j - 1) % N] + grid[(i + 1) % N, (j + 1) % N]) / 255)
            # 生命更新规则
            if grid[i, j] == ON:
                if (total < 2) or (total > 3):
                    newGrid[i, j] = OFF
            else:
                if total == 3:
                    newGrid[i, j] = ON
    # 更新数据
    img.set_data(newGrid)
    grid[:] = newGrid[:]
    return img,


def main():
    # 接收传入的参数
    parser = argparse.ArgumentParser(description="Runs Conway's Game of Life simulation.")
    parser.add_argument('--grid-size', dest='N', required=False)
    parser.add_argument('--mov-file', dest='movfile', required=False)
    parser.add_argument('--interval', dest='interval', required=False)
    parser.add_argument('--glider', action='store_true', required=False)
    parser.add_argument('--gosper', action='store_true', required=False)
    args = parser.parse_args()

    # 设置默认地图尺寸
    N = 100
    if args.N and int(args.N) > 8:
        N = int(args.N)

    # 设置默认更新间隔时间ms毫秒
    updateInterval = 50
    if args.interval:
        updateInterval = int(args.interval)

    # 选择起始图像
    grid = np.array([])
    # 没有选择则使用随机图像
    if args.glider:
        grid = np.zeros(N * N).reshape(N, N)
        addGlider(1, 1, grid)
    elif args.gosper:
        grid = np.zeros(N * N).reshape(N, N)
        addGosperGliderGun(10, 10, grid)
    else:
        grid = randomGrid(N)

    # 设置动画
    fig, ax = plt.subplots()
    img = ax.imshow(grid, interpolation='nearest')
    ani = animation.FuncAnimation(fig, update, fargs=(img, grid, N,),
                                  frames=10,
                                  interval=updateInterval,
                                  save_count=50)

    # 选择输出位置
    if args.movfile:
        ani.save(args.movfile, fps=30, extra_args=['-vcodec', 'libx264'])

    plt.show()


# 运行
if __name__ == '__main__':
    main()

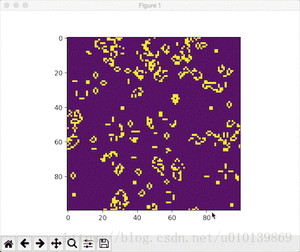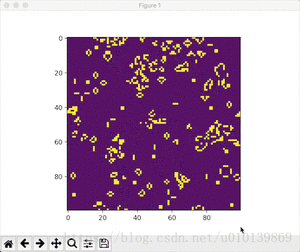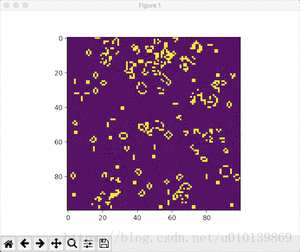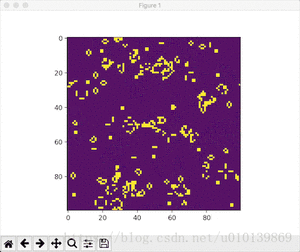
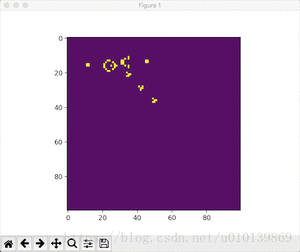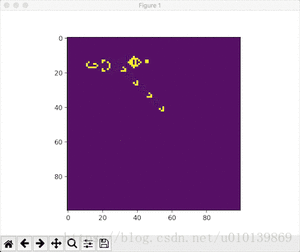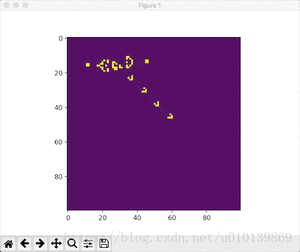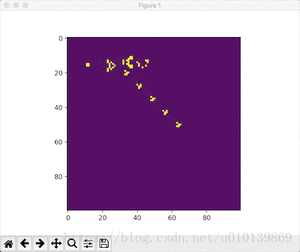
效果展示

  • Conway随机初始条件
python conway.py
Conway随机初始条件
  • Conway滑翔机
python conway.py --glider
Conway滑翔机
  • Conway发射器
python conway.py --gosper
Conway发射器
  • 其他参数
地图大小
python conway.py --grid-size
输出位置
python conway.py --mov-file
刷新间隔（ms）
python conway.py --interval

主要研究领域

组合博弈论

康威因其对组合博弈论(CGT)的贡献而广为人知，这是一种党派博弈理论。他与 Elwyn Berlekamp 和 Richard Guy 共同发展了这一理论，并与他们合著了《数学游戏的制胜之道(Winning Ways for your Mathematical Plays)》一书。他还写了CGT 的数学奠基之作——《关于数字和游戏(On Numbers and Games)》(ONAG)。

他还是豆芽游戏(sprouts)和哲球棋(Phutball)的发明者之一。他给出了索马立方(Soma cube)、孔明棋(Peg solitaire)、康威的士兵(Conway's Soldiers)等许多其他游戏和谜题的详细分析。他提出了天使问题(angel problem)，该问题在2006年已获解答。

他创立了一种新的数字系统——超现实数(surreal numbers)，这些数字与某些游戏密切相关，并成为唐纳德·克努斯(Donald Knuth)的数学中篇小说的主题。他还为大数发明了一种表示方法——康威链式箭号表示法(Conway chained arrow notation)，这个方法可以表示连高德纳箭号表示法都难以表示的数。

几何学

在20世纪60年代中期，康威与迈克尔·盖伊(Michael Guy)建立了64个凸均匀多面体(convex uniform polychora)，其中不包括两个棱形无穷集。 他们在这个过程中发现了巨大的反棱镜，这是唯一的非维索菲安式均匀多面体(non-Wythoffian uniform polychoron)。此外，康威创立了一个用于描述多面体的符号系统，称为康威多面体表示法(Conway polyhedron notation)。

康威提出了一种密铺数学理论——康威准则(Conway criterion)，描述多边形可用来做平面镶嵌的条件。

他研究了更高维度的晶格，并首次确定了利奇格(Leech lattice，24维欧几里得空间的一种双幺模晶格)的对称群。

几何拓扑学

在纽结理论中，康威对亚历山大多项式(Alexander polynomial)的一个版本进行公式化，并产生了一个新的不变量——康威多项式(Conway polynomial)。在沉寂了十多年之后，这个概念在20世纪80年代成为新纽结多项式(knot polynomials)的核心。康威进一步发展了缠结理论(tangle theory)，并发明了一种描述纽结的符号系统——康威符号(Conway notation)。

群论

康威是给出许多有限简单群(finite simple groups)的性质的《有限群的阿特拉斯(ATLAS of Finite Groups)》的第一作者。他与同事罗伯特·柯蒂斯(Robert Curtis )和西蒙 · p·诺顿(Simon P. Norton)一起构建了一些散在群(sporadic groups)的第一个具体表述。具体来说，他根据利奇格(Leech lattice)的对称性发现了三个散在群，它们被命名为康威群(Conway groups)。这项工作使他成为有限单群分类的关键人物。

1979年，康威和西蒙·诺顿(Simon P. Norton)提出怪兽月光理论(monstrous moonshine)，表达了怪兽群(monster group)和模函数(modular functions)间的惊人关系，这一理论沟通了原本分立的有限群理论和复函数理论。怪兽月光理论现已经被发现与弦理论有着深刻的联系。

康威引入了Mathieu groupoid，它是马蒂厄群M12(Mathieu group M12)扩展到13点而来。

数论

康威研究生时证明了爱德华·华林(Edward Waring)的一个猜想，即每个整数都可以写成37个数字的的五次方之和。（陈景润在康威的著作出版之前独立地解决了这个问题。）

代数

代数方面，康威写过教科书，做过尤其是四元数(quaternions)和八元数(octonions)方面的原创性工作。他和尼尔·斯隆(Neil Sloane)一起发明了icosian。

分析

康威给出介值定理(intermediate value theorem)逆命题的一个反例——康威十三进制函数: 满足强达布性质(Darboux property)，但不是连续的。

算法

为了某天是星期几，康威发明了末日规则(Doomsday rule)。这个算法非常简单，任何一个有基本算术能力的人都可以心算得出答案。康威通常能在两秒钟内给出正确答案。

理论物理学

2004年，康威和另一位普林斯顿的数学家西蒙(Simon B. Kochen)证明了自由意志定理(free will theorem)，这是量子力学的无隐变量(no hidden variables)原理一个惊人版本。它指出，在某些条件下，如果实验者可以自由决定在特定实验中测量什么量，那么基本粒子必须能够自由选择其自旋，以使测量结果与物理定律一致。康威挑衅性的措辞是: “如果实验者有自由意志，那么基本粒子也有。”

荣誉奖项

  • 贝里克奖(Berwick Prize)，1971年
  • 皇家学会院士(FRS)，1981年
  • Pólya Prize(LMS，伦敦数学学会)首位获奖者，1987年
  • 内默斯数学奖(Nemmers Prize in Mathematics)，1998年
  • 美国数学学会2000年数学博览会勒罗伊·P·斯蒂尔奖(Leroy P. Steele Prize)
  • 英国数学协会荣誉会员，2017年

博士生导师

哈罗德·达文波特 Harold Davenport

学生

理查德·博赫兹 Richard Borcherds

罗伯特·威尔逊 Robert Wilson

就职企业、机构或院校

应用与计算数学约翰·冯·诺伊曼教授(John von Neumann Professor)，荣誉退休

著作

  • Regular Algebra and Finite Machines, Chapman and Hall, Ltd. London, 1971.
  • All Numbers Great and Small, Research Paper No. 149, Calgary, Alberta, Canada: The University of Calgary, Dept. of Mathematics and Statistics, 1972.
  • All Games Bright and Beautiful, Research Paper No. 295, Calgary, Alberta, Canada: The University of Calgary, Dept. of Mathematics and Statistics, 1975.
  • On Numbers and Games, London Mathematical Society Monographs, No. 6, Academic Press, London-New-San Francisco, 1976.
  • (with E.R. Berlekamp and R.K. Guy), Winning Ways, for Your Mathematical Plays, Vol. 1: Games in General, Vol. 2: Games in Particular, New York-London: Academic Press, 1982, ISBN 0120911027, Paperback (August, 1982), Academic Press, ISBN 0120911027.
  • (with R.T. Curtis, S.P. Norton, R.A. Parker and R.A. Wilson), Atlas of Finite Groups: Maximal Subgroups and Ordinary Characters for Simple Groups, Oxford, Clarendon Press, New York, Oxford University Press, 1985.
  • (with N.J.A. Sloane), Sphere Packings, Lattices, and Groups, (with additional contributions by E. Bannai, J. Leech, S.P. Norton, A.M. Odlyzko, R.A. Parker, L. Queen and B.B. Venkov), Grundlehren der Mathematischen Wissenschaften, 209, Springer-Verlag, New York, 1988, ISBN 0-387-96617-X, Russian Translation: Mir, Moscow, 1990, 2nd edition 1993, ISBN 0-387-97912-3, 3rd edition 1998, ISBN 0-387-98585-9.
  • (with R.K. Guy), The Book of Numbers, Copernicus. An Imprint of SpringerVerlag, New York, 1996, ISBN 0-387-97993-X, Review by Ian Stewart. Review by Susan Stefney, Corrected 2nd printing, 1998.
  • (with Francis Y.C. Fung), The Sensual (Quadratic) Form, MAA (Series: Carus Mathematical Monographs), Printed in the U.S.A., 1997, ISBN 0-88385-030-3.
  • (with N.J.A. Sloane), The Geometry of Low-Dimensional Groups and Lattices, (in preparation).
  • (with D. Smith), “Quaternions, Octonions, and Geometry,” AK Peters, Publishers, January 2003. preparation).

更多论文点击John H. Conway Bibliography

人物介绍和报道

  • A Life in Games：约翰·何顿·康威声称他一生中从未有一天是在工作。 此文根据传记《游戏中的天才(Genius at Play)》改编，展示了诸如超现实数(surreal numbers)之类的重大突破是如何从娱乐和游戏中产生的。《量子杂志(Quanta Magazine)》，西沃恩·罗伯茨(Siobhan Roberts)
  • John Horton Conway Dean of the Faculty, Princeton University

视频

更多信息

wiki词条

百度词条

CV

普林斯顿大学数学系个人主页

参考文献

  1. ↑ "John Conway". The Royal Society. Retrieved April 11, 2020.{{cite web}}: CS1 maint: url-status (link)
  2. ↑ Conway, J. H.; Hardin, R. H.; Sloane, N. J. A. (1996). "Packing Lines, Planes, etc.: Packings in Grassmannian Spaces". Experimental Mathematics. 5 (2): 139. arXiv:math/0208004. doi:10.1080/10586458.1996.10504585.
  3. ↑ 约翰·何顿·康威 John Horton Conway's publications indexed by the Scopus bibliographic database. (subscription required)
  4. ↑ Conway, J. H.; Sloane, N. J. A. (1990). "A new upper bound on the minimal distance of self-dual codes". IEEE Transactions on Information Theory. 36 (6): 1319. doi:10.1109/18.59931.
  5. ↑ Conway, J. H.; Sloane, N. J. A. (1993). "Self-dual codes over the integers modulo 4". Journal of Combinatorial Theory, Series A. 62: 30–45. doi:10.1016/0097-3165(93)90070-O.
  6. ↑ Conway, J.; Sloane, N. (1982). "Fast quantizing and decoding and algorithms for lattice quantizers and codes" (PDF). IEEE Transactions on Information Theory. 28 (2): 227. CiteSeerX 10.1.1.392.249. doi:10.1109/TIT.1982.1056484.
  7. ↑ Conway, J. H.; Lagarias, J. C. (1990). "Tiling with polyominoes and combinatorial group theory". Journal of Combinatorial Theory, Series A. 53 (2): 183. doi:10.1016/0097-3165(90)90057-4.
  8. ↑ 8.0 8.1 MacTutor History of Mathematics archive: John Horton Conway
  9. ↑ "John Conway". www.nndb.com. Retrieved 10 August 2010.
  10. ↑ 10.0 10.1 "CONWAY, Prof. John Horton". Who's Who 2014, A & C Black, an imprint of Bloomsbury Publishing plc, 2014; online edn, Oxford University Press.(subscription required)
  11. ↑ Roberts, Siobhan (23 July 2015). "John Horton Conway: the world's most charismatic mathematician". The Guardian.
  12. ↑ Mark Ronan (18 May 2006). Symmetry and the Monster: One of the greatest quests of mathematics. Oxford University Press, UK. pp. 163. ISBN 978-0-19-157938-7. https://archive.org/details/symmetrymonstero0000rona. 
  13. ↑ Gardner, Martin (October 1970). "Mathematical Games: The fantastic combinations of John Conway's new solitaire game "Life"". Scientific American. Vol. 223. pp. 120–123.
  14. ↑ "DMOZ: Conway's Game of Life: Sites". Archived from the original on 17 March 2017. Retrieved 11 January 2017.
  15. ↑ LifeWiki
  16. ↑ Does John Conway hate his Game of Life? (video)
  17. ↑ MacTutor History: The game made Conway instantly famous, but it also opened up a whole new field of mathematical research, the field of cellular automata.
  18. ↑ Rendell (2015)
  19. ↑ Case (2014)

本中文词条由费米子编辑，欢迎在讨论页面留言。

本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。

取自“https://wiki.swarma.org/index.php?title=约翰·何顿·康威_John_Horton_Conway&oldid=2786”