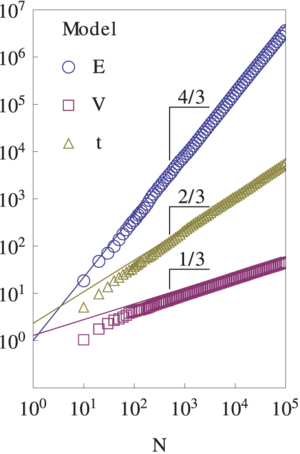“匹配生长随机几何图模型”的版本间的差异
| 第165行: | 第165行: | ||
当模型运行足够长时间,网络生长到足够大的时候,整个网络会逐渐趋向于一个对称的球形形状。如下图: | 当模型运行足够长时间,网络生长到足够大的时候,整个网络会逐渐趋向于一个对称的球形形状。如下图: | ||
| − | [[File:shape1.png|300px]][[File:shape2.png|300px | + | [[File:shape1.png|300px]][[File:shape2.png|300px]] |
这提示我们随着规模的增大,随机模型中的那些局部涨落就会被抹平,所以整个网络趋向于一个普通的欧几里得几何体。于是,我们尝试用平均场方法来对模型进行分析。 | 这提示我们随着规模的增大,随机模型中的那些局部涨落就会被抹平,所以整个网络趋向于一个普通的欧几里得几何体。于是,我们尝试用平均场方法来对模型进行分析。 | ||
| 第358行: | 第358行: | ||
这个分布P<sub>N</sub>虽然无法精确求解,但它的数值近似为一个Zipf定律。于是,我们得到了在稳态情况下,团簇的尺度分布服从Zipf律。 | 这个分布P<sub>N</sub>虽然无法精确求解,但它的数值近似为一个Zipf定律。于是,我们得到了在稳态情况下,团簇的尺度分布服从Zipf律。 | ||
| − | |||
==基本模型Python代码== | ==基本模型Python代码== | ||
2022年1月20日 (四) 21:40的版本
在很多复杂系统的生长过程中都会体现出两类特殊的现象,即相互作用的超线性生长以及多样性的亚线性生长。也就是说,如果我们将生长的复杂系统看作是一个复杂网络,那么网络的连边数通常会比网络的节点数增长得更快;与此同时,网络中节点的种类数(多样性)则会比节点数增长得更慢。这两种现象都可以用一个统一的方程予以描述,即
[math]\displaystyle{ Y\propto N^{\gamma} }[/math]
其中Y可以表示网络中的连边数或者网络节点的种类数,而N表示的是网络中的节点数。大量的实证研究发现,这两个变量在生长的过程中会满足上述幂律方程,其中如果Y表示的是连边数,则指数[math]\displaystyle{ \gamma\gt 1 }[/math],而如果Y表示的是节点种类数,则指数[math]\displaystyle{ \gamma\lt 1 }[/math]。
为了解释这两类现象,我们提出了匹配生长的随机几何图模型(Matching Growth Random Geometric Graph Model)[1][2]。该模型用简单的假设解释了这两类现象,并且在基础模型基础上,我们可以扩展该模型,于是我们可以模拟城市生长等现象。
基本模型
模型基本假设
该模型假设网络是单调生长的,也就是说系统中的节点和连边都只能生长,而不能减少;其次,我们假设网络中的所有节点都可以被嵌入一个欧氏空间中,并且每一个节点具有一个欧氏空间坐标。再次,我们假设节点和节点的相互作用是局部的;最后,只有能够与现有节点发生相互作用的新增节点才能存在下去。
模拟结果
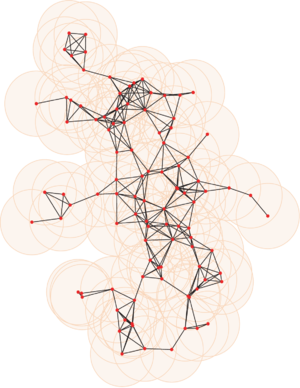
按照上述规则,模型可以一直演化下去,下图展示的是在2维空间中,有100个节点加入之后的网络形状:
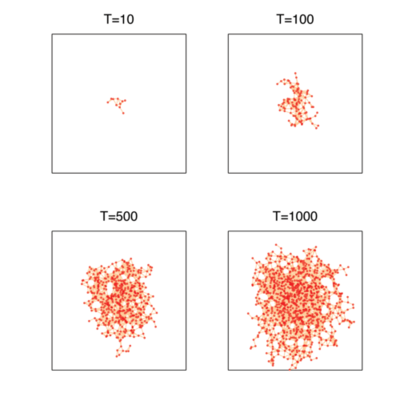
下图展示的是网络在不同时间点的形状:
我们可以看到,网络在不同的时间步会一直不停地生长下去。
加速生长特性
该模型的生长会体现出明显的加速特性,也就是说,在开始的时候网络生长得很慢;而随着网络长大,网络的生长速度也会越来越快。这是因为,每个周期新节点都是随机地生长出来,然而由于在初始时刻,已存在的节点覆盖面积非常小,所以新生长的节点有较小的概率能够存活下去;反过来,随着网络越长越大,已存活节点所覆盖的面积也会逐渐增大,所以新加入的点就会以较大的概率落入被已存在节点覆盖的范围之内。这样,网络越大就会越快地累积新的节点,一种正反馈机制就会建立起来,从而使得网络能够加速生长下去。
密集化趋势
在网络长大的过程中,网络会在空间分布上体现出异质性。对于中心的区域来说(种子节点附近),因为每个周期新加入的节点刚好落在这片区域的机会都一样,所以随着时间的推移,这片区域的节点会越积累越多。反过来,对于远离中心的节点来说,由于在开始时刻这个区域附近没有已存活的节点,所以新节点几乎不可能在这里得到生长,只有当网络逐渐扩大以使得该区域附近充满了已存活的节点的时候,新节点进入该区域的概率才不为零。所以远离中心的节点会更加稀疏。因此,最后的网络节点会在中心区域密集化。对于任何一个区域来说,由于节点数只增不减,所以节点密度也是始终增加的。
链接超线性生长
下面,我们来考虑平均每增加一个节点所带来的连边数。显然,新加入的节点既可能进入中心区域也可能进入外围区域。但无论新节点落入哪一个区域,它的连边数都取决于周围邻居的数量,而这个数量正如前所述是在不停地增加的,所以每加入一个新节点所带来的连边数就会单调地增加下去。于是,连边数就会比节点数增加的更快。这就是链接的超线性生长现象。
多样性亚线性生长
另一方面,我们不妨用这些已存在节点所覆盖的面积作为整个网络中节点的多样性度量。那么,我们会发现,多样性会比网络节点数更缓慢的增长。我们不妨将已存在节点覆盖的区域分成中心和外围两种区域。每个新加入并存活的节点更可能在中心区域存活,而加入这些区域是不会扩大网络所覆盖的面积的,只有当新加入的节点刚好位于整个覆盖区域的外围的时候,整个覆盖区域的面积才会增长。于是,随着网络增大,覆盖区域也在增大,中心区域也在增大,于是新节点落入外围区域的概率就会减小,从而使得网络的覆盖面积会比节点数长得慢,这就是多样性的亚线性生长现象。
定量模拟结果
上述各种现象都可以用定量的模拟结果加以展示,如下图所示:
在其中,横坐标N表示的是网络中的节点数,纵坐标表示的分别是E:连边数、V:网络覆盖的面积即多样性、t:模型运行的时间。我们看到,E、V、t都随着网络的节点数增长而呈现幂律的增长。但是这三个幂律指数分别为4/3、2/3,和1/3,这说明V和t比N增长的慢,这正是多样性减速生长特性和整个网络加速生长特性的体现(节点数随t越涨越快)。同时,我们能够得到连边数E和节点数N之间的超线性幂律关系,这也是与实证中看到的现象相符合的。
解析结果
注意到,虽然模型的运转完全是随机的,生成的网络图形也是极其不规则的。但是,当网络长大、节点数变多之后,实际上局部的随机涨落就会越来越不明显,网络呈现将会明显地呈现出各向同性和对称性。因此,在这个时候,我们便可以用平均场近似的处理方法来做。
当网络的节点数足够大之后,我们会得到如下渐近的性质:
网络连接的超线性生长规律,即
[math]\displaystyle{ E\propto N^{\frac{d+2}{d+1}} }[/math]
这里E表示网络的连边数,N表示网络的节点数,d为空间的维度
除此之外,多样性的亚线性生长规律也可以被解析地得到:
[math]\displaystyle{ V\propto N^{\frac{d}{d+1}} }[/math]
这里,V表示网络的覆盖体积。
最后,网络的加速生长性质可以表达成:
[math]\displaystyle{ t\propto N^{\frac{1}{d+1}} }[/math]
这里,t为模型运转的时间。比较这些结果和上一节的模拟结果不难看出,我们的解析解与模拟解得到了完全相同的幂律指数。
模型扩展
拥挤模型
在基本模型中,节点的生长会发生聚集。尤其是在种子节点附近的位置,节点数可以达到任意多。这样,根据模型的设定,种子节点应该与所有周围的节点建立连接。然而,这个设定显然与真实情况不一致。在真实世界中,任何一个生态都不可能容纳无限多的新的节点。当某个位置的节点聚集过多,则节点之间就会产生竞争排斥作用,这导致新的节点不容易被加入。
为了模拟这种竞争排斥作用,我们可以在基础模型的基础上添加新的拥挤规则。具体地,每一个周期,新节点仍然随机地在Ld中产生,当新节点与某个已存在节点足够临近,它就具备了加入网络的可能性。但是,这个新节点并不确定性的加入网络,而是以概率Π加入,或者以概率1-Π无法加入。这个概率Π取决于该位置的已存在节点密度。如果在X处已存在节点密度为ρ(X),那么:
[math]\displaystyle{ \Pi=\rho(X)^{-\alpha} }[/math]
这里,α是一个给定的参数,称为拥挤系数,它的取值介于[math]\displaystyle{ [0,\infty) }[/math]之间。也就是说,如果X处的已存在节点密度过高,则新节点成功加入网络的可能性就会降低。而拥挤系数α则衡量了这个概率对节点密度的敏感性。当α=0的时候,概率Π=1,也就是说新节点保证能加入,这就回到了我们的基础模型。反过来,如果[math]\displaystyle{ \alpha \rightarrow \infty }[/math]那么Π就几乎为零,这就形成了确定性的排斥作用,即如果X处有节点,新节点就不能加入。α越大,竞争排斥作用就会越强。
当我们引入了新的模型后,模型会发生什么变化呢?我们发现,基础模型中的优良性质仍然被保留了下来。连接的超线性增长和多样性的亚线性增长现象仍然存在,但是这个时候幂律指数就不仅仅依赖于维度d,还依赖于参数α。具体地,我们有:
[math]\displaystyle{ E\propto N^{1+\frac{1}{1+(1+\alpha) d}} }[/math]
[math]\displaystyle{ V\propto N^{\frac{(1+\alpha) d}{1+(1+\alpha) d}} }[/math]
所以,当d给定的时候,E和N的指数,以及V和N的指数都会随着α而变。
异质化模型
在基础模型中,我们假设每个节点的作用范围r都是一样的。但是在现实中,每个人的影响力都会不同,有大有小。我们假设,每个节点的影响力r是一个随机变量,并且假设这个随机变量满足一个指数或者拉伸指数的概率分布,也就是:
[math]\displaystyle{ r\sim exp(-\lambda x^{\beta}) }[/math]
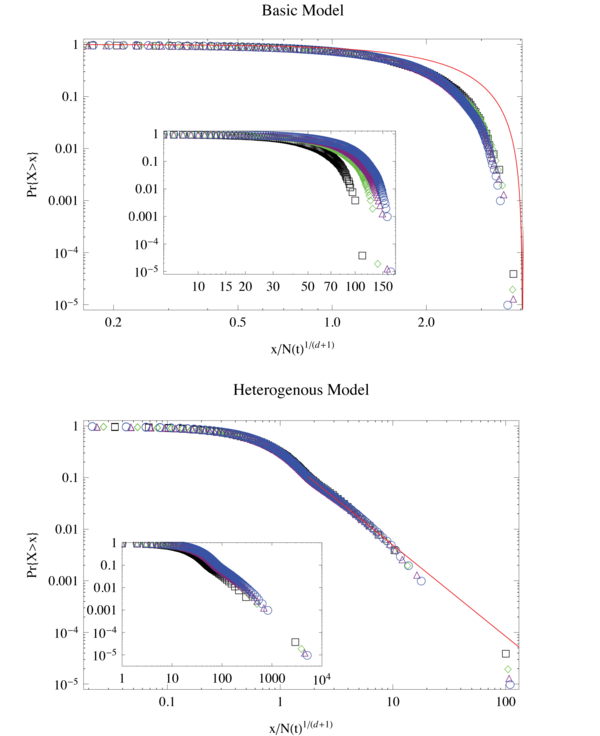
这里,λ和β是两个自由参数。最后得到的网络是一个无标度网络,也就是网络的度分布满足幂律分布特征,下图展示了基本模型和这个扩展的异质化模型的度分布情况。我们同时画出了模型在不同规模的情况下的度分布。与此同时,模型还可以保留连接数的超线性生长和多样性的亚线性生长的特性。因此这是一个同时得到超线性增长和无标度网络的网络模型。
空间吸引模型
在基本模型中,每一个周期产生的新点都在全空间内等概率地选择出生地。然而,这也是一个不必要的选择。一个有意思的选择是我们在X点生成新点的概率Z是与该点的已存活点的密度ρ(X)有关的。经过反复的试验,我们发现当:
[math]\displaystyle{ Z(X)\propto \rho(X)+C }[/math]
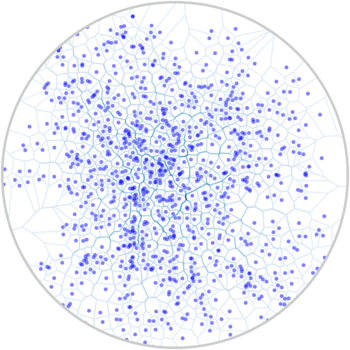
的时候,模型能够产生非常有意思的结果。如果固定d=2,则该模型可以模拟出真实城市的形态。如下左图展示的就是模型生成的节点情况,右图则绘制了伦敦的人口分布形态,这二者有很高的相似度。
C是一个模型中的唯一参数,它可以在0到无穷大中间取任意的数值。由于已存在点越多的地方就会有更多的新点产生,从而让新点更好地附着到整个网络上,所以,我们称这个模型为空间吸引模型。我们发现,当C取不同数值的时候,最后形成的已存活点的空间分布满足如下方程:
[math]\displaystyle{ \rho(r)\propto r^{-\beta}(R_t^{1+\beta}-r^{1+\beta})\sim r^{-\beta} }[/math]
这里\rho(r)表示距离中心(种子节点)r处已存活节点的密度。β是一个唯一依赖于C的指数,我们无法得到β(C)的解析表达式,但可以给出数值模拟的结果,它随着C呈现幂律加指数截断方式的衰减。Rt为t时刻整个网络的半径(定义为从中心点到最远存活点的距离)。当r远远比Rt,上述表达式可以近似地表达成r-β的形式。
这是从理论上得到的节点密度分布情况。经过大量的实证研究我们发现,城市中的活跃人口分布也满足完全相同的分布形式。其中,活跃人口与普通的居住人口或工作人口不同,它是一种居住与工作按照人们的工作时长进行混合的人口密度,它表达的是城市中任何一个空间点的平均人流密度。我们发现,至少对于北京和伦敦这两座城市来说,它们的活跃人口分布完全符合这种形式。但是,不同的城市具有完全不同的β数值,具体如图所示:
我们看到,伦敦的β取值为0.3,北京的取值相应为0.1。除此之外,如果加入额外的假设,我们还能够很好地模拟出城市道路和城市中社会经济相互作用密度随空间的分布情况。有关更多的讨论,可以参看空间吸引模型
模型的平均场方法求解
下面我们来考虑这个基本模型的求解,即给出数学上的描述。乍一看,这是一个随机生长模型,每一步节点的添加似乎都仅仅依赖于上一步模型的整个状态,因而我们可以用马尔可夫链的方法对其进行建模。但是,仔细分析就会发现由于每一步节点的产生都与其它的所有节点产生相关性,我们无法从一般的马尔可夫随机过程中得到解决。
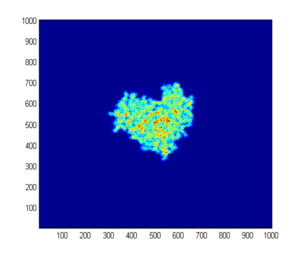
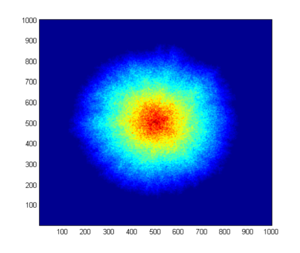
当模型运行足够长时间,网络生长到足够大的时候,整个网络会逐渐趋向于一个对称的球形形状。如下图:
这提示我们随着规模的增大,随机模型中的那些局部涨落就会被抹平,所以整个网络趋向于一个普通的欧几里得几何体。于是,我们尝试用平均场方法来对模型进行分析。
高维情况
虽然我们没办法给出高维情况下更严格的理论证明,但经过我们反复的试验,我们发现网络模型的半径R(t)随着时间线性地生长的确是成立。我们可以给出近似的求解办法。
如图:
在一般的维度d>1的情况下,我们将R(t)定义为t时刻离种子最远的一个存活点到种子的距离。让我们考虑它的生长ΔR。由于在平均场情况下(模型足够大,运行时间足够长),模型网络是一个各向同性的几何图形,因此在每一个单独方向上,模型都相似于一个一维的模型。这样,我们只需要分析任意一个方向即可。如果要想让ΔR>0,那么新的点必然会在最外围点的r半径的d维球内(如上图的阴影区域)。因为每一次新产生的随机点都会均匀地在整个Ld超立方体内分布。所以,这个新的点落入到这个阴影区域内的概率就会正比于这片区域的面积。当R(t)非常大的时候,这块区域的体积近似于一个半径为r的d维球的一半。因此,ΔR的平均值就是:
[math]\displaystyle{ \langle \Delta R\rangle =\frac{\int_{(|x|\lt r)\and(x_1\gt 0) }x_1 d\sigma}{L^d} }[/math] [math]\displaystyle{ =\int_0^rd\rho \int_0^{\pi/2}d\theta_1\int_0^{\pi}d\theta_2\cdot\cdot\cdot\int_0^{2\pi}d\theta_{d-1} \rho \cos(\theta_1)\rho ^{d-1} \sin(\theta_1)^{d-2}\sin(\theta_2)^{d-3}\cdot\cdot\cdot \sin(\theta_{d-1}) }[/math] [math]\displaystyle{ =\frac{V_{d-1}r^{d+1}}{(d+1)L^d} }[/math]
这里Vd-1是d维单位球的体积。x1是d维点的第一个坐标。也就是说,每个周期网络半径的增长量期望也是一个常数。那么,网络的期望半径为:
[math]\displaystyle{ \langle R(t)\rangle =\frac{V_{d-1}r^{d+1}}{(d+1)L^d}\cdot t }[/math]
于是,网络的半径与t成正比。
节点密度
解出了网络半径的生长规律之后,模型的性质就很容易解出来了。首先,根据R正比于t的思路,我们不难想到,在平均场的图景下,模型网络在空间中就是一个对称的半径为R(t)的球,它要均匀地增长。
下面,我们就来考虑任意时刻t在任意一个空间点(坐标(ρ,Θ),这是极坐标,极径是ρ,级角Θ是一堆角构成的向量)的已存在节点的密度μ(ρ,Θ,t)。我们知道,根据平均场的假定,半径ρ处在τ(ρ)时刻以前是完全没有任何节点的。这里τ(ρ)是网络的半径刚刚长到ρ时候所用的时间步,我们知道τ和ρ是正比的。所以,只有从τ(ρ)时刻后,ρ半径处的这个点才开始接收节点。并且,在每一个仿真周期,这一点接收新节点落入的概率是完全一样的。这是因为按照基本模型每个点落入空间任意点都是等概率的。于是,在经过了t-τ(ρ)时间步后,(ρ,Θ)这个位置积累的点的数量就是:
[math]\displaystyle{ \mu(\rho,\Theta,t)=\int_{\tau(\rho)}^{t}(d\sigma /L^d) ds \propto (t-\tau(\rho)) d\sigma/L^d\propto R(t)-\rho }[/math]
这里,dσ表示一个无限小微元的体积,(dσ/Ld)是每一个周期落到(ρ,Θ)点的概率。总体上看,该点处的点密度是正比于网络增长到该点的时刻τ到t时刻的时间的,也正比于网络在t时刻的半径与ρ之差。
有了这个表达式,我们不难求出整个球内点的总量为:
[math]\displaystyle{ N(t)=\int \mu(\rho,\Theta,t) \rho d \rho d\Theta \propto R(t)^{d+1} }[/math]
我们又知道,点(ρ,Θ)处的节点密度为μ(ρ,Θ),而每一个节点要与它所有邻近的节点发生链接,于是这一点的连边密度就是μ(ρ,Θ)2。于是,再对这个密度做积分,我们不难得到整个网络的连边数为:
[math]\displaystyle{ E(t)=\int \mu(\rho,\Theta,t)^2 \rho d\rho d\Theta \propto R(t)^{d+2} }[/math]
而因为这个球是一个欧氏几何体,所以它的体积就是:
[math]\displaystyle{ V(t)\propto R(t)^d }[/math]
于是,根据上面三个式子,消去R(t),我们便可以得到各种标度律了:
[math]\displaystyle{ E(t)\propto N(t)^{\frac{d+2}{d+1}} }[/math]
[math]\displaystyle{ V(t)\propto N(t)^{\frac{d}{d+1}} }[/math]
[math]\displaystyle{ t\propto R(t)\propto N(t)^{\frac{1}{d+1}} }[/math]
网络的其它属性
根据上面的推论,我们不难得出网络的其它属性。例如,网络的度分布为(度为x的节点数为):
[math]\displaystyle{ f_D(x)=\frac{1}{N(t)^{1/(d+1)}}g(\frac{x}{N(t)^{1/(d+1)}}) }[/math]
这里,
[math]\displaystyle{ g(y)=\frac{d(1+d)y(1-y/k)^d}{k(k-y)} }[/math]
[math]\displaystyle{ k=(1+d)(\frac{V_{d-1}}{V_d})^{-\frac{d}{d+1}} }[/math]
而网络的平均簇系数为:
[math]\displaystyle{ C=\frac{3 \Gamma(\frac{d+2}{2})}{\sqrt{\pi}\Gamma(\frac{d+1}{2})}\int_0^{\pi/3}\sin^d\theta d\theta }[/math]
拥挤模型求解
拥挤模型与基础模型的不同之处在于即使落点周围有其它的邻居,它也不一定存活,它能否存活的可能性取决于这个点的点密度。首先,我们发现,这个新假设的引入并不影响平均场分析的基础假设
[math]\displaystyle{ R(t)\propto t }[/math]
这是因为新产生的点仍然是等可能地在整个d维立方体中均匀地进行着,所以上面的分析步骤仍然适用于这个拥挤模型。于是,某一点处的点数仍然是网络长到这个位置后到达t时刻的积累总量。但是,情况不同的是,一旦这个点处出现了点,那么排斥作用就会发生,这就导致我们不容易给出解析表达式。
事实上,我们可以对该点的点密度写出一个微分方程,如下:
[math]\displaystyle{ \frac{\partial \mu(\rho,\Theta,t)}{\partial t} = \frac{1}{L^d} \mu(\rho,\Theta,t)^{-\alpha} }[/math]
也就是说,如果(ρ,Θ)这一点要想增长一个点,那么它的概率就要正比于随机落点选择该点的概率乘以这个新的点不被排斥的概率。所以,该点的概率增长率也就是这个方程所列。同时,我们需要注意到初始条件:
[math]\displaystyle{ \mu(\rho,\Theta,\tau(\rho))=0 }[/math]
求解这个微分方程就会得到新的节点密度为:
[math]\displaystyle{ \mu(\rho,\Theta,t)=\frac{(t-\tau(\rho))^{\frac{1}{1+\alpha}}}{L^d} }[/math]
这样,就可以类似地得到:
[math]\displaystyle{ N(t)\propto R(t)^{d+\frac{1}{1+\alpha}} }[/math]
[math]\displaystyle{ E(t)\propto R(t)^{d+\frac{2}{1+\alpha}} }[/math]
多种子模型
不失一般性,我们在二维空间中考察多种子模型。如果L足够大,那么不同的种子所形成的团块不会发生重叠的情况。这个时候,每一个团块就是一个独立的生长网络,因此上述的各种结论仍然适合于每一个团块。
其次,我们可以分析这些团块经过一段时间生长后的尺度分布情况。假设这些团块的节点数分别为N1, N2,...,NC,则它们的面积就是
[math]\displaystyle{ V_i=b N_i^{\eta}=b N_i^{\frac{2+2\alpha}{3+2\alpha}} }[/math]
其中指数η<1是拥挤模型得到的结论。
由于每次产生的新点都等概率地落在超级立方体的某处,所以它落到第i个团簇的概率就会正比于这个团簇的面积Vi。而落入的点就会成为i的一个新节点,从而使得Ni增长,从而导致它的面积增加。于是这就形成了一个正反馈的过程:越大的团簇有越高的机会吸引新点加入进去。
实际上,这是一个亚线性的偏好依附模型。如果我们用系统中已存活的节点数s为时间尺度,那么系统每一个周期就会增长一个点。设当系统中一共有s个存在节点的时候,拥有N个节点的团簇个数为MN(s),那么我们可以写下M的增长方程:
[math]\displaystyle{ \frac{\partial M_N(s)}{\partial s}=\frac{1-\epsilon}{b Z}[b(N-1)^{\eta}M_{N-1}(s)-bN^{\eta}M_N(s)]+\epsilon \delta_{N=1} }[/math]
这里[math]\displaystyle{ Z=\sum_{N=1}^{\infty}N^{\eta}M_N(s), \delta_{N=1} }[/math]为一个狄拉克Delta函数,当N=1的时候为1,否则为0。进一步,我们定义
[math]\displaystyle{ P_N(s)=M_N(s)/N_C(s) }[/math]
为s时刻,包含N个节点的团簇所占的比例。那么经过整理,可以得到方程:
[math]\displaystyle{ \epsilon P_N(s)+\epsilon s \frac{\partial P_N(s)}{\partial s}=\epsilon s\frac{1-\epsilon}{Z}[(N-1)^{\eta}P_{N-1}(s)-N^{\eta}P_N(s)]+\epsilon \delta_{N=1} }[/math]
当[math]\displaystyle{ s\rightarrow \infty }[/math]的时候,我们有[math]\displaystyle{ \frac{\partial P_N(s)}{\partial s}=0 }[/math],于是就能得到:
[math]\displaystyle{ P_N(s)=s \frac{1-\epsilon}{Z}[(N-1)^{\eta}P_{N-1}(s)-N^{\eta}P_N(s)]+\epsilon \delta_{N=1} }[/math]
于是可以解出来当[math]\displaystyle{ s\rightarrow \infty }[/math]的时候:
[math]\displaystyle{ P_N=\zeta N^{-\eta}\exp[-\zeta (\frac{N^{1-\eta}-2^{1-\eta}}{1-\eta})] }[/math]
这里
[math]\displaystyle{ \frac{1-\epsilon}{\epsilon}=\sum_{N=1}{\infty}\Pi_{j=1}^{N}(1+\zeta/j^{\eta})^{-1} }[/math]
这个分布PN虽然无法精确求解,但它的数值近似为一个Zipf定律。于是,我们得到了在稳态情况下,团簇的尺度分布服从Zipf律。
基本模型Python代码
基本的编程思路比较简单,但是如果严格按照模型表述,则由于每一步都要随机在Ld的立方体中生成点,就会导致大量的点无法附着在网络上,造成不必要的计算浪费。于是,编程的时候采用了一个技巧就是,每次新生成点都是在一个围绕着整个已有网络的ad超级立方体里面撒点,这里的a为当前网络的最大直径+2r。这样就可以保证每次落点都尽可能地有效,将区域外的无畏测试扔掉,又能保证模型规则的保留。
import numpy as np
from scipy.sparse import *
from scipy import *
import random
import matplotlib.pyplot as plt
import pickle
import networkx as nx
from scipy.optimize import leastsq
from rtree import index #必备包,为了让模型加速
def initiate(L,d,r):
#input: L range, d dimension, r radius
#generate nodes that carry coordinates
coordinate=np.ones(d)*L/2
nodelist={1:{1:coordinate,3:1,4:0,5:0}}
#1: coordinate, 3: borning time, 4: In degree, 5: out degree
# Create 2D index, Using Rtree to accelerate
p = index.Property()
if d>=2:
p.dimension = d
else:
p.dimension = 2
idxnd = index.Index(properties=p)
limitt=np.zeros(2*d)
for key in nodelist:
ele=nodelist[key]
xs=ele[1]
rectangle1=xs-r
rectangle2=xs+r
if d==1:
idxnd.insert(key,[rectangle1,0,rectangle2,0])
else:
idxnd.insert(key,list(np.r_[rectangle1,rectangle2]))
limitt=np.r_[rectangle1,rectangle2]
# nodelist: a list of nodes, idxnd: Rtree indices, limitt: Rectangle boundary
return (nodelist,idxnd,limitt)
def onestep(nodelist,idxnd,L,network,limit,time,d,r):
#计算几何图占方形区域面积
aa=1
for i in range(d):
aa=aa*(limit[i+d]-limit[i])
locallambda=aa/(L**d)
#Bias sample the area of aa (valid area) to accelerate. And the average time interval between two random valid nodes
# follow an exponential distribution, some time can generated virtually
time+=random.expovariate(locallambda)
#Generate a random node within the valid area
newpoint=np.array([random.random()*(limit[d+v]-limit[v])+limit[v] for v in range(d)])
#Search for neighbors
if d==1:
hits=list(idxnd.intersection((newpoint,0,newpoint,0)))
else:
hits=list(idxnd.intersection(tuple(np.r_[newpoint,newpoint])))
neighbors={}
newedges=0;
if len(hits)>0:
for i in hits:
node=nodelist[i]
distance=np.linalg.norm(node[1]-newpoint)
if distance<r:
ind=i
neighbors[i]=ind
if len(neighbors)>0:
# Real adding nodes and links
nodelist[len(nodelist)+1]={1:newpoint,3:time,4:0,5:len(neighbors)}
for i in range(d):
limit[i]=min(limit[i],newpoint[i]-r)
limit[i+d]=max(limit[i+d],newpoint[i]+r)
for nd in neighbors:
node=nodelist[nd]
node[4]=node[4]+1
newedges=newedges+1
if d==1:
idxnd.insert(len(nodelist),[newpoint-r,0,newpoint+r,0])
else:
rectangle1=newpoint-r;
rectangle2=newpoint+r;
rectangle=np.r_[rectangle1,rectangle2];
idxnd.insert(len(nodelist),rectangle)
return (nodelist,idxnd,newedges,network,limit,time)
# -----------------
#---------Experiment 1: Basic implementation
#-----------------
L=10**10#Hypercube length
maxnode=10**5#The wanted number of nodes
d=2#spatial dimension
r=1#interaction area;
ndlist,idx,limit=initiate(L,d,r)
t=1
edges=[0];
network={};
time=1
while len(ndlist)<maxnode:
ndlist,idx,newedge,network,limit,time=onestep(ndlist,idx,L,network,limit,time,d,r)
if newedge>0:
edges=np.r_[edges,edges[-1]+newedge];
if np.remainder(t,1000)==0:
print len(ndlist)
t=t+1;
参考文献
- ↑ Zhang, Jiang (2015). "Scaling behaviors in the growth of networked systems and their geometric origin". Scientific Reports. 5: 9767.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ↑ Zhang, Jiang date = 2012. "Growing Random Geometric Graph Models of Super-linear Scaling Laws".
{{cite journal}}: Cite journal requires|journal=(help); Missing pipe in:|first=(help)
编者推荐
集智课程
[]
本中文词条薄荷编辑,如有问题,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。