“自复制自动机”的版本间的差异
| 第71行: | 第71行: | ||
== 各实例间的比较 === | == 各实例间的比较 === | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{| class="wikitable sortable" | {| class="wikitable sortable" | ||
!实例 | !实例 | ||
| 第269行: | 第209行: | ||
正如冯诺依曼所定义的,通用构造过程的产物只包含被动“被”构建的结构。因此,通用构造器的概念只不过是一种设想(或是数学)结构。尽管它有助于其他的证明,比如构造良好的机器有可能会自我复制,但通用构造过程本身只是在最简单情况下的设想。此标准下的通用构造概念是不值一提的。因此,尽管这里给出的所有结构都可以构建出新的相似结构(新结构仅能被动的“被”构建),但没有一个可以实现Gorman 设计的实时交互机制 Real-Time Crossing Organ。<ref name="Automata2008" /> | 正如冯诺依曼所定义的,通用构造过程的产物只包含被动“被”构建的结构。因此,通用构造器的概念只不过是一种设想(或是数学)结构。尽管它有助于其他的证明,比如构造良好的机器有可能会自我复制,但通用构造过程本身只是在最简单情况下的设想。此标准下的通用构造概念是不值一提的。因此,尽管这里给出的所有结构都可以构建出新的相似结构(新结构仅能被动的“被”构建),但没有一个可以实现Gorman 设计的实时交互机制 Real-Time Crossing Organ。<ref name="Automata2008" /> | ||
| − | |||
== 实用性和计算成本 == | == 实用性和计算成本 == | ||
2022年3月12日 (六) 22:20的版本
冯·诺依曼的通用构造器 Universal Constructor是一个在元胞自动机(后称CA)环境中的自复制机。它是在20世纪40年代没有使用计算机的情况下设计的。自复制自动机的基本细节发表在了冯·诺依曼的著作《自复制自动机理论 Theory of Self-Reproducing Automata》中,该书由亚瑟·伯克斯 Arthur W. Burks于冯·诺依曼去世后的1966 年完成。[2] 虽然自复制自动机不像冯诺依曼的其他成就那样广为人知,但它被认为是自动机理论 Automata Theory、复杂系统和人工生命的基础。[3][4]并且,诺贝尔奖得主悉尼布伦纳 Sydney Brenner认为冯·诺依曼提出的自复制自动机(及其计算机)也是生物学理论的核心,让后人能够规范化的思考自然和人造机器。[5]
冯·诺依曼1949年在伊利诺伊大学厄巴纳-香槟分校的演讲中提到,[2]他的目标是设计一种复杂性可以自动增长(类似于自然选择下有机生命体)的机器。当被问到机器要跨越多高的复杂性阈值才能够进化时,[4]他给出了一个抽象的自复制机模型。在他的设计中,自复制机包含三个组件:1、关于自身结构的“描述文件”(类似于蓝图或编码);2、能够阅读并按照任何“描述文件”构建机器的通用构造模块 Universal Constructor Mechanism,但构建过程不包括生成“描述文件”;3、能够复制任何“描述文件”的通用复制模块 Universal Copy Machine。在通用构造模块基于“描述文件”构建新机器后,使用通用复制模块生成该“描述文件”的副本并放入到新机器中,进而生成该自复制机的复制。有些自复制机会先复制“描述文件”,然后再构建新机器并放入。但无论顺序如何,自复制机 可以通过累积“描述文件”的突变来进化(获得复杂性增长),而不是通过机器自身的变化来实现复杂性的增长。[4][5] (译者:可类比物种的进化是种群基因形的逐渐变化而非某一生物个体突然进化。)
为了更详细地定义自复制机,冯诺依曼提出了元胞自动机的概念。元胞自动机由二维网格单元组成,每个单元在任何单位时间段都可以处于29种状态中的一种。在每个单位时间段中,每个单元格都根据上一个单位时间段周围单元格的状态更新其状态。所有单元的更新规则都是相同的。(译者:规则有很多,比如上一时间段周围八格里有一格处于状态一,那么这一时间段这一格就变成状态一。)
通用构造器是该元胞自动机中的特定状态变化模式。它包含一行作为“描述文件”的单元格(类似于图灵指令磁带 Turing's tape),上面编码了一系列构建指令作为构建机器的“蓝图”。自复制机逐条读取这些指令并执行相应的操作,使用它的“构造臂”(通用构造模块,其功能类似于操作系统 [4])在元胞自动机的其他单元网格处建立一个不包含“描述文件”的自复制机副本。需要注意:“描述文件”携带的信息量不足以包含用于构建自身的说明,就像容器不能包含相同大小的容器一样。因此,该机器还要包括单独的通用复制模块,该模块读取并复制“描述文件”,然后将副本放入新建的机器内。新生成的一组通用构造模块、通用复制模块和“描述文件”与旧的相同,并且会再次进行复制。
目的
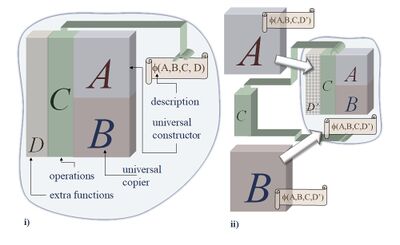
冯·诺依曼的设计传统上被理解为是用于展示机器自我复制的逻辑要求。[3]然而,更简单的机器也可以实现自我复制,比如微观的晶体状生长、模板复制 template replication和朗顿循环 Langton's loops。因此,事实上冯·诺依曼关注的是更为深刻的概念:建构、普遍性和进化。[4][5]
由于简单的自我复制 CA 结构(特别是Byl循环和Chou-Reggia循环)不能以多种形式存在,因此可进化性非常有限。其他 CA 结构(例如Evoloop)在某种程度上是可进化的,但仍然不支持开放式进化。通常,简单的复制器不包含通用构建模块,在某种程度上是被动由周围环境复制的信息(构造相似结构)。尽管冯诺依曼设计是一种逻辑结构,但原则上它是一种可以被实例化为物理机器的设计。这个通用构造模块可以看作是对物理通用汇编器 Physical Universal Assembler的抽象模拟。环境对复制的影响这一问题有些开放,因为对原材料及其可用性有很多不同的概念。
冯·诺依曼的重要贡献是机器的“描述文件”,通过通用复制模块复制并传递给后代的过程具有具有双重用途:既是再生产中建构机制的主动组成部分,又是被动复制过程的目标。这一部分由冯·诺依曼的通用构造模块、通用复制模块和“描述文件”中的“描述文件”(类似于图灵的指令磁带)来扮演。[4]通用构造模块、通用复制模块和“描述文件”的组合概念化并形式化了:i) 自我复制。ii)开放式进化或在生物有机体中观察到的复杂性增长。[3]
冯·诺依曼的这一贡献非常引人注目,因为它的提出是在Watson和Crick发现DNA的双分子结构以及它如何在细胞中单独翻译和复制之前(尽管是在Avery-MacLeod-McCarty实验将DNA确定为活生物体遗传信息的分子载体之后)。[6]DNA分子通过不同的化学机制进行处理,这些机制执行其指令(翻译)并复制出新构建细胞的DNA。实现开放式进化的能力在于,类似于自然界基因,复制过程中的错误(突变)可能产生自动机的有效变体,然后自动机可以通过自然选择进化。[4] 正如布伦纳 Brenner 所说:
“图灵发明了存储程序计算机,冯·诺依曼证明了“描述文件”和通用构造模块是分开的。这不是小事,物理学家埃尔文·薛定谔(Erwin Schrödinger)在其 1944 年的著作《生命是什么? What is Life?》中混淆了“描述文件”和通用构造模块。在这本书中,他将染色体视为“建筑师的计划和建筑者的工艺融为一体”是错误的。“描述文件”只包含对功能(构建新机器与复制“描述文件”)的描述,而不包括本身。”
复杂性的演变
正如 1949 年在伊利诺伊大学的演讲中所指出的,[2]冯·诺依曼的目标是设计一种机器,其复杂性可以自动增长(类似于自然选择下的生物有机体)。在被问到机器要跨越多高的复杂性阈值才能够进化并不断复杂时,[4] [3]他的“理论证明”有着逻辑上的可能性。通过使用将通用可编程“通用”构造模块与复制模块分开的架构,他展示了机器的“描述文件”(磁带)如何在自我复制中积累突变,从而进化出更复杂的机器(下图说明这种可能性)。这一贡献之所以重要,是因为在此之前的人们可能会认为这种机器逻辑上根本无法存在:人们都曾认为能够进化和增长复杂性的生物(有机体)不可能是传统意义上的“机器”。而冯·诺依曼的见解则是将生命视为一台状态确定的图灵机,它受与存储磁带(“描述文件”)相分离的“磁头”所定义。[5]
在实践中,当考虑冯·诺依曼所追求的特定自动机实例时,结论是它不会产生太多的进化动力学,因为机器太脆弱了——绝大多数扰动会导致它们的瓦解。[3] 因此,如今更令人感兴趣的是他在伊利诺伊州的讲座中概述的概念模型,[2]因为它展示了机器在理论上是如何进化的。[7][4]概念模型之所以更加引人注目,因为该模型先于上述讨论的 DNA 双分子结构的发现。[6]还值得注意的是,冯·诺依曼的设计认为,向更复杂的突变只发生在“描述文件”中,而非个体的其他部分,以此来实现所有的无论是否参与复制过程中的功能,正如自动机D 的那样(见上图,具有进化能力的冯·诺依曼自复制自动机系统)。实际上,在生物有机体中也只能观察到遗传基因非常微小的变化,这与冯·诺依曼的原理相吻合,即通用构造模块(A)和通用复制模块(B)不会自己发展,而是将所有的进化(和复杂性的增长)交给自动机(D)。[4] 在他未完成的作品中,冯·诺依曼还简要考虑了他的自复制机之间的冲突和相互作用,以从他的自复制机理论中理解生态和社会的演变。[2]
实例
在自动机理论中,由于伊甸园模式的存在,通用构造模块的概念非常重要。但一个简单的定义是,通用构造模块能够构造任何有限模式的非激发(静止)细胞。
Arthur Burks等人扩展了冯·诺依曼的工作,给出了更清晰和完整的自复制机设计和操作细节。撒切尔JW Thatcher的作品尤其值得一提,因为他大大简化了设计。尽管如此,他们的工作并没有产生能够逐个单元地展示自复制实例的完整设计。
1995 年,Renato Nobili和 Umberto Pesavento 发表了第一个完全实现的自复制元胞自动机,距冯·诺依曼的提出已近 50 年。[1][8] 他们使用32态元胞自动机代替冯诺依曼最初的29态规则,通过对其进行了扩展,实现了更轻松的信号交叉、显式记忆功能和更紧凑的设计。他们还在最初的 29 态 CA 中发布了一个通用构造模块的实现,但它不能完全复制——机器不能复制它的磁带,也不能激发它构建的后代,只能构建不包含“描述文件”的机器。[8][9]
2004 年,D. Mange 等人实现了与冯·诺依曼设计一致的自复制机。[10]
2007 年,Nobili 发布了一个 32 态规则的实例,它使用游程编码来大大减小磁带的大小。[11]
2008 年,威廉·R·巴克利 William R. Buckley发表了两种结构,它们是冯·诺依曼最初的29态 CA 中的自我复制器。[9]巴克利声称冯诺依曼 29 态元胞自动机内的信号交互对于构建自复制机不是必需的。[9]他还指出,为了进化的目的,每个自复制机在复制后都应该恢复到原来的结构,以便能够在理论上制造多个副本。正如发表的那样,1995 年的 Nobili-Pesavento 设计不满足这一要求,但 2007 年 Nobili的设计以及Buckley的结构却满足了这一要求。
2009 年,Buckley 与Golly 一起发布了 von Neumann 29 态元胞自动机的第三种结构,它可以执行整体自我复制,也可以通过部分构造进行自我复制。这种结构还表明,在冯诺依曼 29 态元胞自动机中构建自复制机不需要信号交互。
2002 年的 CL Nehaniv,以及2004年的 Y. Takada 等人,提出了一种直接在异步元胞自动机上实现的通用构造模块,而不是在同步元胞自动机上实现。[12]
[13]
各实例间的比较 =
| 实例 | 来源 | 规则集 | 矩形区域 | 单元数 | 磁带长度 | 比率 | 周期 | 磁带编码压缩 | 带码长度 | 带码类型 | 复制机制 | 复制类型 | 增长率 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 诺比利-佩萨文托,1995[1] | [14] | 诺比利 32 态 | 97 × 170 | 6,329 | 145,315 | 22.96 | 6.34 × 10 10 | 无 | 5 位 | 二进制 | 整体构造器 | 不可重复 | 线性 |
| 诺比利, 2007 | SR_CCN_AP.EVN[11] | 诺比利 32 态 | 97 × 100 | 5,313 | 56,325 | 10.60 | 9.59 × 10 9 | 游程限制编码 | 5 位 | 二进制 | 整体构造器 | 可重复 | 超线性 |
| 巴克利,2008 | codon5.rle[15] | 诺比利 32 态 | 112×50 | 3,343 | 44,155 | 13.21 | 5.87 × 10 9 | 自动回退 | 5 位 | 二进制 | 整体构造器 | 可重复 | 线性 |
| 巴克利,2008[9] | replicator.mc | 冯诺依曼 29 态 | 312 × 132 | 18,589 | 294,844 | 15.86 | 2.61 × 10 11 | 自动回退 | 5 位 | 二进制 | 整体构造器 | 可重复 | 线性 |
| 巴克利,2008 | codon4.rle[15] | 诺比利 32 态 | 109 × 59 | 3,574 | 37,780 | 10.57 | 4.31 × 10 9 | 自动回退/位生成 | 4 位 | 二进制 | 整体构造器 | 可重复 | 线性 |
| 巴克利,2009 | codon3.rle | 诺比利 32 态 | 116 × 95 | 4,855 | 23,577 | 4.86 | 1.63 × 10 9 | 自动回退/位生成/代码覆盖 | 3 位 | 二进制 | 整体构造器 | 可重复 | 超线性 |
| 巴克利,2009 | PartialReplicator.mc[15] | 冯诺依曼 29 态 | 2063 × 377 | 264,321 | 无 | — | ≈1.12 × 10 14 | 无 | 4 位 | 二进制 | 部分构造器 | 可重复 | 线性 |
| 古彻和巴克利,2012 | phi9.rle[16] | 诺比利 32 态 | 122×60 | 3957 | 8920 | 2.25 | — | 自动回退/位生成/代码覆盖/运行长度限制 | 3+ 位 | 三进制 | 整体构造器 | 可重复 | 超线性 |
正如冯诺依曼所定义的,通用构造过程的产物只包含被动“被”构建的结构。因此,通用构造器的概念只不过是一种设想(或是数学)结构。尽管它有助于其他的证明,比如构造良好的机器有可能会自我复制,但通用构造过程本身只是在最简单情况下的设想。此标准下的通用构造概念是不值一提的。因此,尽管这里给出的所有结构都可以构建出新的相似结构(新结构仅能被动的“被”构建),但没有一个可以实现Gorman 设计的实时交互机制 Real-Time Crossing Organ。[9]
实用性和计算成本
冯诺依曼的自复制机的实现都需要相当多的资源才能在计算机上运行。例如,在上面给出的 Nobili-Pesavento 32 态实例中,虽然机器主体只有 6,329 个非空单元(在 97x170 大小的矩形内),但它需要一个长 145,315 个单元的磁带,需要 63十亿个时间步来复制。以每秒 1,000 个时间步长运行的模拟器需要 2 年多的时间来制作第一个副本。1995 年,当第一个实例发布时,作者还没有看到他自己的机器复制。然而,在 2008 年,hashlife算法被扩展到支持Golly 中的 29 态和 32 态规则集。在现代的桌面 PC 上,尽管需要大量的内存,但复制只需要几分钟。
动画画廊
参见
参考文献
- ↑ 1.0 1.1 1.2 Pesavento, Umberto (1995), "An implementation of von Neumann's self-reproducing machine" (PDF), Artificial Life, MIT Press, 2 (4): 337–354, doi:10.1162/artl.1995.2.337, PMID 8942052, archived from the original (PDF) on June 21, 2007
- ↑ 2.0 2.1 2.2 2.3 2.4 von Neumann, John; Burks, Arthur W. (1966), Theory of Self-Reproducing Automata. (Scanned book online), University of Illinois Press, retrieved 2017-02-28
- ↑ 3.0 3.1 3.2 3.3 3.4 McMullin, B. (2000), "John von Neumann and the Evolutionary Growth of Complexity: Looking Backwards, Looking Forwards...", Artificial Life, 6 (4): 347–361, doi:10.1162/106454600300103674, PMID 11348586, S2CID 5454783
- ↑ 4.00 4.01 4.02 4.03 4.04 4.05 4.06 4.07 4.08 4.09 4.10 Rocha, Luis M. (1998), "Selected self-organization and the semiotics of evolutionary systems", Evolutionary Systems, Springer, Dordrecht: 341–358, doi:10.1007/978-94-017-1510-2_25, ISBN 978-90-481-5103-5
- ↑ 5.0 5.1 5.2 5.3 5.4 Brenner, Sydney (2012), "Life's code script", Nature, 482 (7386): 461, doi:10.1038/482461a, PMID 22358811, S2CID 205070101
- ↑ 6.0 6.1 6.2 6.3 Rocha, Luis M. (2015), "Chapter 6. Von Neumann and Natural Selection." (PDF), Lecture Notes of I-485-Biologically Inspired Computing Course, Indiana University (PDF)
- ↑ Pattee, Howard, H. (1995), "Evolving self-reference: matter symbols, and semantic closure", Communication and Cognition Artificial Intelligence, Biosemiotics, 12 (1–2): 9–27, doi:10.1007/978-94-007-5161-3_14, ISBN 978-94-007-5160-6
- ↑ 8.0 8.1 Nobili, Renato; Pesavento, Umberto (1996), "Generalised von Neumann's Automata", in Besussi, E.; Cecchini, A. (eds.), Proc. Artificial Worlds and Urban Studies, Conference 1 (PDF), Venice: DAEST
- ↑ 9.0 9.1 9.2 9.3 9.4 Buckley, William R. (2008), "Signal Crossing Solutions in von Neumann Self-replicating Cellular Automata", in Andrew Adamatzky; Ramon Alonso-Sanz; Anna Lawniczak; Genaro Juarez Martinez; Kenichi Morita; Thomas Worsch (eds.), Proc. Automata 2008 (PDF), Luniver Press, pp. 453–503
- ↑ Mange, Daniel; Stauffer, A.; Peparaolo, L.; Tempesti, G. (2004), "A Macroscopic View of Self-replication", Proceedings of the IEEE, 92 (12): 1929–1945, doi:10.1109/JPROC.2004.837631, S2CID 22500865
- ↑ 11.0 11.1 Nobili, Renato (2007). "The Cellular Automata of John von Neumann". Archived from the original on January 29, 2011. Retrieved January 29, 2011.
- ↑ Nehaniv, Chrystopher L. (2002), "Self-Reproduction in Asynchronous Cellular Automata", 2002 NASA/DoD Conference on Evolvable Hardware (15-18 July 2002, Alexandria, Virginia, USA), IEEE Computer Society Press, pp. 201–209
- ↑ Takada, Yousuke; Isokawa, Teijiro; Peper, Ferdinand; Matsui, Nobuyuki (2004), "Universal Construction on Self-Timed Cellular Automata", in Sloot, P.M.A. (ed.), ACRI 2004, LNCS 3305, pp. 21–30
- ↑ 引用错误:无效
<ref>标签;未给name属性为:4的引用提供文字 - ↑ 15.0 15.1 15.2 引用错误:无效
<ref>标签;未给name属性为sourceforge.net的引用提供文字 - ↑ 引用错误:无效
<ref>标签;未给name属性为:0的引用提供文字
外部链接
- Golly-元胞自动机模拟加速器 非常快速地实现状态转换并支持 JvN、GoL、Wolfram 和其他系统。
- 冯·诺依曼的自我复制通用构造模块 复制机的原始Nobili-Pesavento源代码,动画和Golly文件。
- 冯·诺依曼的 29 态元胞自动机在 OpenLaszlo 中的实现 Don Hopkins提供。
- 自复制元胞自动机目录 该目录是对Proc 的补充。自动机 2008卷。