稳定性理论

此词条由Bnustv整理和审校

在数学上，稳定性理论 Stability theory被用于研究微分方程Differential equation解的稳定性和动力系统 Dynamical system在初始条件的微小扰动下轨迹的稳定性问题。例如，热传导方程 Heat equation是一个稳定的偏微分方程，因为极大值原理 Maximum principle的存在，初始数据的微小扰动会导致温度随之产生微小的变化。在偏微分方程中，人们可以使用 [math]\displaystyle{ Lp }[/math] 范数或 [math]\displaystyle{ sup }[/math] 范数来度量函数之间的距离，而在微分几何中，人们可以使用Gromov–Hausdorff距离来度量空间之间的距离。

在动力系统中，如果一条轨道 Orbit上任意点的前向轨道都处于一个足够小的邻域内，或者这条轨道整体停留在一个邻域（一般是较小的邻域，也有可能是较大的邻域）内，则称该轨道的状态为李雅普诺夫稳定 Lyapunov stable。有各种标准来证明轨道的稳定性或不稳定性。在适当的条件下，这个问题可以简化为一个涉及矩阵特征值 Eigenvalue的问题，关于这类矩阵特征值的问题已被大量研究并且该领域已经比较成熟。一种更一般的方法涉及李雅普诺夫函数 Lyapunov function。在实践中，很多稳定性判据 Stability criterion都可以使用，我们可以使用其中的任何一个作为判断系统稳定性的准则。

稳定性图将庞加莱映射 Poincaré map 根据其特征划分为稳定或不稳定区间。如图可见，图中下半部分区域中系统的稳定性增加。

常微分方程在经历了长期的求精确解的努力后逐渐停滞，庞加莱在分析的基础上引入几何方法，开创了常微分方程定性理论，同时在分析中引入几何方法，搭建起分析与几何之间的沟通桥梁，带来了微分方程研究的新突破。李雅普诺夫则在庞加莱定性分析的基础上 ,转而进入了新的稳定性研究。如今 ,李雅普诺夫稳定性理论被普遍认为是微分方程定性理论的基本成就之一。不仅有精确的定义 ,更有严格的分析证明 ,将微分方程及稳定性理论的研究推向了新的高度。庞加莱被公认是19世纪后四分之一和二十世纪初的领袖数学家，是对于数学和它的应用具有全面知识的最后一个人，他在数学方面的杰出工作对20世纪和当今的数学造成极其深远的影响。庞加莱映射 Poincaré map是由相空间中轨道运动定义的一种映射，是当轨道反复穿越同一截面时，反映后继点对先行点依赖关系的映射。一个连续非线性动力系统的求解是非常困难的，庞加莱给出了相图分析法。在相图中虽然不能定量地知道物理量随时间的变化，但可以定性地得到轨线的形态类型及其拓扑结构，从而了解动力系统运动的全局图像。为了更清楚了解高维相空间运动的形态，在连续运动的轨线上用一个截面（称庞加莱截面）将其横截，轨线在截面上穿过的情况就可以简捷地判断运动的形态。对于庞加莱映射是稳定的还是不稳定的判断则取决于其特征，如图所示，在相空间区间中向下的方向上稳定性增加。

动力系统概述

微分方程和动力系统定性理论的许多部分关心系统或者方程解的渐近性质及其轨迹，这也意味着系统经过很长时间后会发生什么。系统最简单的行为表现为平衡点 Equilibrium points或不动点，以及周期轨道 Periodic orbit。如果我们已经很好地理解了一个特定的轨道，那么很自然地就会问下一个问题：初始条件的一个微小变化对于系统来说是否仍会保持类似的行为。稳定性理论解决了以下问题：附近的轨道是否会无限靠近给定的轨道？已知的轨道会收敛到给定的轨道吗？在前一种情况下，轨道被称为是稳定 Stable的；在后一种情况下，轨道是渐近稳定 Asymptotically stable 的，并且收敛到给定的轨道称为吸引子 Attractor。

对于一个一阶常微分方程自治系统的平衡解[math]\displaystyle{ f_e }[/math]：

• 如果对于任意（小的）[math]\displaystyle{ \epsilon \gt 0 }[/math]，存在[math]\displaystyle{ \delta \gt 0 }[/math]，使得只要初始条件与平衡点的距离在[math]\displaystyle{ \delta }[/math]范围内，例如[math]\displaystyle{ \| f(t_0) - f_e \| \lt \delta }[/math]，就有，对任何[math]\displaystyle{ t \ge t_0 }[/math]满足解 [math]\displaystyle{ f(t) }[/math] 与平衡点的距离在 [math]\displaystyle{ \epsilon }[/math] 范围内，例如[math]\displaystyle{ \| f(t) - f_e \| \lt \epsilon }[/math]，那么该平衡点称为稳定的。

• 如果该平衡点是稳定的，并且存在 [math]\displaystyle{ \delta_0 \gt 0 }[/math]，使得对于任何[math]\displaystyle{ \| f(t_0) - f_e \| \lt \delta_0 }[/math]，当[math]\displaystyle{ t \rightarrow \infty }[/math]时都有[math]\displaystyle{ f(t) \rightarrow f_e }[/math]，那么该平衡点是渐近稳定的。

稳定性意味着在微小的扰动下轨迹不会发生太大的变化。相反的情况中，微小的扰动会使得轨迹发生较大变化，即附近的轨道与给定的轨道互相排斥，这也是一种有趣的现象。一般来说，在某些方向对初始状态的扰动使得轨道渐近地接近给定轨道，而在其他方向的扰动则使得轨道远离给定轨道。也可能存在对初始状态在某些方向的扰动使得轨道行为变得比较复杂（比如既不会收敛也不会完全逃逸），从而稳定性理论不能对于这样的动力学状态给予充分的预测信息。

稳定性理论的关键思想之一是用轨道附近系统的线性化，来分析轨道在扰动下的定性行为。特别地，在 n 维相空间 Phase space的光滑动力系统的每个平衡点上，都存在一个 n×n 的矩阵 A，其特征值刻画了邻近点的动力学行为（Hartman-Grobman 定理 Hartman–Grobman theorem）。更确切地说，如果矩阵所有的特征值都是负实数或实部为负的复数，那么这个平衡点就是一个稳定的吸引子，并且附近的点以指数速率收敛到它，参考李雅普诺夫稳定性 Lyapunov stability和指数稳定性 Exponential stability。如果所有的特征值都不是纯虚数(或零) ，那么吸引方向和排斥方向都与矩阵 A 的特征空间有关，其特征值的实部分别为负和正。对于更复杂的轨道上的扰动情形，也有类似的表述。

不动点稳定性

最简单的一种轨道就是一个不动点，称为平衡态，或者叫做平衡点。如果一个力学系统处于稳定的平衡状态，那么只需要一个很小的推力就会导致局部运动的发生，例如，类似钟摆那样的小规模的振动。在有阻尼的系统中，稳定的平衡态是渐近稳定的。另一方面，对于一个不稳定的平衡，例如一个球停留在山顶的最高顶点上，一个极其微小的推力就会导致一个大幅度的运动，这个运动可能会也可能不会收敛到原始状态。

对于线性系统而言，存在许多行之有效的测试方法来检验线性系统的稳定性。非线性系统的稳定性通常可以首先考虑其线性化的系统，并从其线性化系统的稳定性中推断出原非线性系统的稳定性。

映射

设 f: R → R是一个连续可微函数，且存在一个不动点a，使得 f(a) = a。

考虑一个通过迭代函数得到的动力系统:

[math]\displaystyle{ x_{n+1}=f(x_n), \quad n=0,1,2,\ldots. }[/math]

当函数 f 在 a 点的导数的绝对值严格小于1时，不动点是稳定的；当在 a 点的导数严格大于1时是不稳定的。这是因为在这个点附近，函数的斜率具有的线性近似值为:

[math]\displaystyle{ f(x) \approx f(a)+f'(a)(x-a). }[/math]

因此

[math]\displaystyle{ x_{n+1}-x_{n} = f(x_n)-x_n \simeq f(a) + f'(a)(x_n-a)-x_n = a + f'(a)(x_n-a)-x_n = (f'(a)-1)(x_n-a) \to \frac{x_{n+1}-x_{n}}{x_n-a}=f'(a)-1 }[/math]

这意味着导数测量的是函数连续迭代接近或偏离不动点 a 的速率。如果不动点 a 处的导数恰好是1或-1，那么就需要更多的信息才能判断系统的稳定性。

对于具有一个不动点 a 的连续可微映射 f: Rⁿ → Rⁿ，存在一个类似的判据，由 a 的雅可比矩阵 J_a(f) 表示。

如果 J 的所有特征值都是绝对值严格小于1的实数或复数，则该点是稳定不动点；

如果J 的所有特征值中至少有一个的绝对值严格大于1，则它是不稳定的。

对于J 的最大特征值的绝对值等于1的情况，需要进一步研究。仅仅使用雅可比矩阵检验是无法确定稳定性类型的。同样的准则对光滑流形的微分同胚情况也有着广泛的适用性。

线性自治系统

利用常系数一阶线性微分方程组对应系数矩阵的特征值，可以分析其不动点的稳定性。

对于一个如下的自治系统 autonomous system

[math]\displaystyle{ x' = Ax, }[/math]

当 x(t) ∈ Rⁿ 且 A 是一个 n×n 的实矩阵时，它具有常数解

[math]\displaystyle{ x(t)=0. }[/math]

[math]\displaystyle{ x_{n+1}=f(x_n), \quad n=0,1,2,\ldots. }[/math]

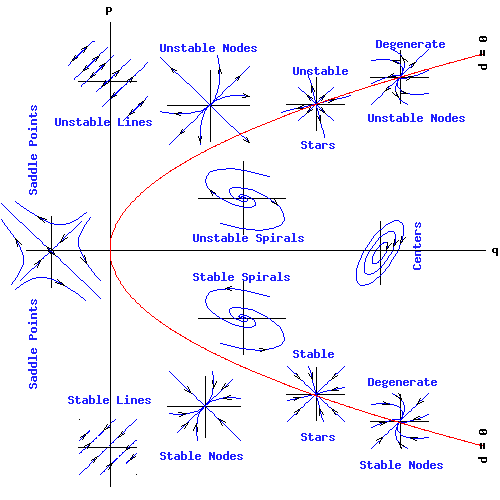
可以这样描述：最初的原点（0 ∈ Rⁿ ） 是该动力系统的平衡点。当且仅当对于A的所有特征值 λ 有 Re(λ) < 0 时，这个解是随着t → ∞是渐近稳定的（未来趋势）。类似地，当且仅当对于 A 的所有特征值 λ 有Re(λ) > 0 时，系统随着t → -∞是渐近稳定的（负号表示方向指向过去趋势）。如果存在一个A的特征值 λ 使得 Re(λ) > 0，则该解在t → ∞时是不稳定的。

为了判定线性系统原点的稳定性，可以使用劳斯-赫尔维茨稳定性判据Routh–Hurwitz stability criterion，来将这一结果应用在实践中。矩阵的特征值是其特征多项式的根。如果所有根的实部都是严格负的，那么一个具有实系数的单变量多项式称为赫尔维茨多项式 Hurwitz polynomial 。劳斯-赫尔维茨定理 Routh–Hurwitz theorem通过一种避免计算根的算法来描述赫尔维茨多项式的特征。

非线性自治系统

非线性系统不动点的渐近稳定性通常可以用 Hartman-Grobman 定理来判断。

假设v是Rⁿ上的一个C¹-向量场，并且下降至某一点p有v(p) = 0。那么相应的自治系统

[math]\displaystyle{ x'=v(x) }[/math]

有一个常数解

[math]\displaystyle{ x(t)=p. }[/math]

设J_p(v)为向量场 v在点p的n×n雅可比矩阵 Jacobian matrix。如果 J 的所有特征值都具有严格负的实部，则系统的解是渐近稳定的。这个条件可以用劳斯-赫尔维茨判据Routh–Hurwitz stability criterion来检验。

一般动力系统的李雅普诺夫函数

建立动力系统的李雅普诺夫稳定性或渐近稳定的一般方法即是利用李亚普诺夫函数来分析。

拓展阅读

• Asymptotic stability 渐近稳定性

• Hyperstability 超稳定性

• Linear stability 线性稳定性

• Orbital stability 轨道稳定性

• Stability criterion 稳定性判据

• Stability radius 稳定半径

• Structural stability 结构稳定性

• von Neumann stability analysis 冯诺依曼稳定性分析

外部链接

• Stable Equilibria 源于Michael Schreiber，Wolfram示范项目。

类别: 极限集

类别: 数学和定量方法(经济学)