反应扩散模型和亚种群模型

此词条由Bnustv整理和审校。

反应扩散过程

(a)基于粒子-网络方案的简化建模框架示意图。在宏观层面上，系统是由一个异质性的亚种群网络组成。由于粒子在亚种群间的扩散，一个亚种群内的传染过程可以传播到其他亚种群。(b)在微观水平上，每个亚种群包含一个个体种群。例如，一种传染现象的动态过程，可以用简单的划分区间来描述(图中不同颜色的点表示这些划分区间)。在每个亚种群中，个体可以均匀地混合扩散，或者基于一个子网络进行混合，在网络混合的方式中个体可以沿着网络的边缘以概率[math]\displaystyle{ p }[/math]的方式从一个亚种群扩散到另一个亚种群。(c)个体或粒子扩散的临界值[math]\displaystyle{ p_c }[/math]确定了在传染影响系统内大部分节点和只影响系统内一小部分节点这两种状态之间的相变。

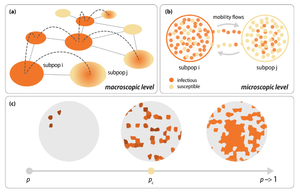
一般而言，社会行为和人类流动性的网络模型通常被构建为以反应-扩散过程 Reaction-Diffusion Processes 为基础，这样的反应扩散模型同时考虑了系统的扩散、迁移和增长，并通常应用于分析空间经济过程之中。在这个网络模型框架中，每个网络中的节点[math]\displaystyle{ i }[/math]可以容纳任何数量为非负整数的粒子[math]\displaystyle{ \mathcal{N}(i) }[/math]，因此系统中的总粒子数为[math]\displaystyle{ \mathcal{N}=\sum_i\mathcal{N}(i) }[/math]。该粒子-网络框架中节点内的每个粒子只能沿着网络中节点之间的连边进行扩散，并且扩散系数取决于节点的度 Node degree或者节点的其他属性。对于不同的系统，节点内粒子之间的反应规则也不同。这样的粒子-网络框架模型的简单示意如右图所示。

为了对网络中的反应扩散系统进行理论上的分析描述，我们允许节点之间具有异质的连接模式。对这些系统的第一种分析方法是考虑将基于节点度的平均场理论方法Degree-based mean-field approach （简称为DBMF方法）扩展到具有任意度分布的反应扩散系统网络中。为简单起见，我们首先考虑在一个简化的系统上应用DBMF方法，这样具有简单网络结构的系统可以描述为：系统的粒子之间没有相互作用或反应，粒子只会在网络上扩散，并且网络可以具有任意的拓扑形式。以这样的描述构建这个系统，我们如果以度[math]\displaystyle{ k }[/math]作为量化指标定义分类的话，可以将系统简单表示为：

\begin{equation} \mathcal{N}_k=\frac{1}{N_k}\sum_{i\in\mathcal{V}(k)}\mathcal{N}(i) \end{equation}

其中[math]\displaystyle{ N_k=NP(k) }[/math]表示网络中度为k的节点数量，[math]\displaystyle{ \mathcal{V}(k) }[/math]表示度为[math]\displaystyle{ k }[/math]的节点集合，[math]\displaystyle{ \mathcal{N}_k }[/math]表示度为[math]\displaystyle{ k }[/math]的节点中包含的平均粒子数。基于度的平均场理论方法（DBMF）近似地假设度为[math]\displaystyle{ k }[/math]的节点是同质的，同理可近似认为节点中的粒子在统计上也是等效的。在这种近似的假设下，粒子随机扩散的动力学可以由如下平均场理论方程表示：

\begin{equation} \frac{d\mathcal{N}_k}{dt}=-d_k\mathcal{N}_k(t)+k\sum_{k'}P(k'|k)d_{k'k}\mathcal{N}_{k'}(t) \end{equation}

方程中的第一项表示在每个单位时间内有比例为[math]\displaystyle{ d_k }[/math]的粒子从度为[math]\displaystyle{ k }[/math]的节点中离开，第二项表示外部粒子从邻居节点扩散到度为[math]\displaystyle{ k }[/math]的节点中，该项与节点的连边数[math]\displaystyle{ k }[/math]成正比，也就是说一个节点与其邻居节点的连接越多，外部粒子扩散进入该节点的可能性越大。条件概率[math]\displaystyle{ P(k'|k) }[/math]表示的是一条边的一端连接度为[math]\displaystyle{ k }[/math]的节点时，其另一端指向度为[math]\displaystyle{ k' }[/math]的概率。[math]\displaystyle{ d_{k'k} }[/math]表示的是两端连接了度为[math]\displaystyle{ k }[/math]和[math]\displaystyle{ k' }[/math]节点的连边的扩散率。在均匀扩散的最简单情况下，每个粒子从其所在的节点以速率[math]\displaystyle{ r }[/math]扩散，因此沿着每条连边的扩散率为[math]\displaystyle{ d_{k'k}=r/k' }[/math]。在无关联的网络上，[math]\displaystyle{ P(k'|k)=k'P(k')/\left\lt k\right\gt }[/math]，因此在稳态[math]\displaystyle{ d\mathcal{N}/dt=0 }[/math]时，很容易得到解（Colizza等，2007b； Noh和Rieger，2004）：

\begin{equation} \mathcal{N}_k=\frac{k}{\left<k\right>}\frac{\mathcal{N}}{N} \end{equation}

上面的公式显式地给出了系统中粒子扩散的描述，并指出网络拓扑结构在反应扩散过程中的重要性。从式中可以看到，如果一个节点的度越大，则其被扩散中的粒子访问到的可能性就越大。

亚种群模型

通过在上述方程中加入反应项，可以将上述方法推广到具有不同状态的粒子发生反应的情形。现在，我们描述在该情形下SIS传播模型Susceptible Infected Susceptible Model 的情况，其中单位时间的感染概率为[math]\displaystyle{ \beta }[/math]，恢复概率为[math]\displaystyle{ \mu }[/math]。我们考虑在具有[math]\displaystyle{ N }[/math]个节点和度分布为[math]\displaystyle{ P(k) }[/math]的异质网络中扩散的[math]\displaystyle{ \mathcal{N} }[/math]个个体。网络的每个节点[math]\displaystyle{ i }[/math]分别具有[math]\displaystyle{ I(i) }[/math]个感染态个体和[math]\displaystyle{ S(i) }[/math]个易感态个体（取值为非负整数值）。这种建模体系描述了空间结构相互作用的亚种群，例如城市位置、城市区域或确定的地理区域，并且通常被称为亚种群方法Metapopulation approach。网络中的每个节点代表一个亚种群，仓室动力学Compartment Dynamics表示了处于相同位置的个体可能会相互接触并根据系统对应的感染动力学改变自身的状态的可能性。亚种群之间的相互作用是个体从一个亚种群迁移到另一个亚种群的结果。为简单起见，我们可以假设个体从他们所在的节点离开沿着任意一条连边扩散的概率为[math]\displaystyle{ p_I=p_S=1 }[/math]。这意味着在每个时间步，度为[math]\displaystyle{ k }[/math]的节点上的一个个体将以概率[math]\displaystyle{ 1/k }[/math]扩散到其最近的邻居之一。为了得到系统的动力学方程，我们定义如下的量：

\begin{equation} I_k=\frac{1}{N_k}\sum_{i\in\mathcal{V}(k)}I(i) \end{equation} \begin{equation} S_k=\frac{1}{N_k}\sum_{i\in\mathcal{V}(k)}S(i) \end{equation}

其中[math]\displaystyle{ \mathcal{V}(k) }[/math]表示度为[math]\displaystyle{ k }[/math]的节点集合。上面的两式表示的是度为[math]\displaystyle{ k }[/math]的节点的平均感染态和易感态个体数，显然有[math]\displaystyle{ \mathcal{N}_k=I_k+S_k }[/math]。 因此基于这些量的定义，我们可以得到随着时间演化的每一类度为[math]\displaystyle{ k }[/math]的节点的系统的动力学方程，表示如下： \begin{equation} I_k(t+1)=k\sum_{k'}P(k|k')\frac{1}{k'}[(1-\mu)I_{k'}(t)+\beta\Gamma_{k'}(t)] \end{equation}

其中[math]\displaystyle{ \Gamma_{k'}(t) }[/math]为相互作用的核，是关于[math]\displaystyle{ I_{k'}$和$S_{k'} }[/math]的函数。该方程是通过考虑在每个时间步，度为[math]\displaystyle{ k }[/math]的节点上的粒子先发生反应，然后以1的概率从节点扩散出去得到的。在无关联网络的情况下，上式可以简化地写为 \begin{equation} I_k(t+1)=\frac{k}{\left<k\right>}[(1-\mu)\bar{I}(t)+\beta\Gamma] \end{equation}

其中[math]\displaystyle{ \bar{I}(t)=\sum_k P(k)I_k }[/math]表示网络中每个节点的平均感染态个体的数量，并且网络中[math]\displaystyle{ \Gamma=\sum_k P(k)\Gamma_k }[/math]。 类似地，描述系统中易感态个体的动力学方程可以表示为 \begin{equation} S_k(t+1)=\frac{k}{\left<k\right>}[\bar{S}(t)+\mu\bar{I}(t)-\beta\Gamma] \end{equation}

其中[math]\displaystyle{ \bar{S}(t)=\sum_k P(k)S_k }[/math]。

参考文献 References

此页参考来源： Pastor-Satorras R, Castellano C, Van Mieghem P, et al. Epidemic processes in complex networks[J]. Reviews of modern physics, 2015, 87(3): 925.